氢原子径向波函数及其分布概率的数值模拟

陈敬仝，刘 锴，吴 坤，张国睿，左亚丽，郑兴荣

(陇东学院 电气工程学院，甘肃 庆阳 745000)

1 引言

氢原子是所有元素中结构最简单的原子，由一个带负电的电子和一个带正电的质子组成，是一个简单的两体系统，同时也是物理学中唯一有解析解的实例[1，2].因此，氢原子在量子力学建立过程及实际应用中有着重要地位，对整个现代量子理论体系的形成起到了举足轻重的作用.所以对氢原子的研究，尤其是本征方程、波函数、电子云及其在空间各点的分布概率有深刻透彻的理解和掌握是必不可少的.随着大数据、云计算和人工智能的发展，量子信息发展较快，我国在量子计算、量子通信和人工智能等尖端科技领域的领先优势[3]，已经向着量子化发展，因此对量子特性的研究势在必得.而氢原子作为现代物理学中唯一有解析解的实例，在许多领域具有重要的作用，如强子物理学、粒子物理学、量子化学、量子力学和材料物理等[4-7].尤其在量子力学里，没有比氢原子问题更简单、更实用，而又有解析解的案例了.另外，运用氢原子及其特性推演出来的基本物理理论，又可以用简单的实验来核对.所以，氢原子问题是个很重要的问题，对其相关特性的进一步研究至关重要[8-11].

近几年对于氢原子及其电子的相关特性研究，已趋于白热化[12-19].球谐函数作为氢原子拉普拉斯本征方程的角向解，其本身及其相关特性的研究很多[13-16]，而径向波函数作为氢原子拉普拉斯本征方程的径向解，近年来却少有研究，或者单纯的只是理论研究[20-24].如2008年陈钢[20]讨论了氢原子径向波函数的“初等”解法，2019年卢欣[21]等人利用变分法得到了氢原子的径向波函数和能级，1994年刘力[22]等人利用径向波函数的振荡性质研究了氢原子径向波函数，1999年魏志勇[23]严格证明了氢原子径向波函数正交归一性，1989年喀兴林[24]等人研究了氢原子径向函数的阶梯算符，基于此，本文在得到氢原子波函数解析解的基础上，单独对波函数径向波函数做了理论推导，并利用MATLAB软件独立、详细地绘制了氢原子径向波函数及其电子空间分布概率的二维图.这种将氢原子径向波函数及其电子空间分布情况形象逼真显示出来的方法，对研究整个氢原子及其轨道的可视化结果具有引导和辅助作用，更对整个量子力学的学习具有重要的指导意义.

2 氢原子径向波函数及其薛定谔方程

对任一氢原子，以原子核为坐标原点，则氢原子的电子受原子核吸引的势能为

(1)

其中：r是电子到核的距离，Z为氢原子核电荷量，es是电子的电荷量，与e的关系为

(2)

(3)

在球坐标系下，式(3)可表示为

(4)

基于数理方法，利用分离变量法[25]求解式(4)，整理可得

(5)

式中：R(r)仅是r的函数，Y(θ，φ)仅是θ和φ的函数.此方程的左边仅与r有关，右边仅与θ，φ有关，而r，θ和φ都是独立变量，所以只有当等式两边都等于同一个常数时，等式(5)才能成立.以λ表示这个常数，则(5)式分离为两个方程：

(6)

(7)

(6)式称为氢原子波函数的径向本征方程，(7)式称为氢原子波函数的角向本征方程，其特性的研究已在前期工作中完成[14].

在前期的工作中[14]，已知

λ=l(l+1)，l=0，1，2，….

代入径向方程(6)式，得

(8)

当E>0时，对于E的任何值，方程(8)都有满足波函数条件的解，即氢原子体系的能量具有连续谱，这使得电子可以离开原子核而运动到无限远处，即可以发生电离.当E<0时，E具有分立谱，电子的状态是束缚态.

借助合流超几何方程，使用合流超几何级数截断为合流超几何多项式，才能满足波函数有界条件[4，25]，则记

β=l+1+nr=n，l=0，1，…，n=1，2，….

(9)

其中：nr为径向量子数，n为总量子数或主量子数.因为nr和l都是正整数或零，所以n=1，2，3….将(9)式代入能量本征值公式中，可得为

(10)

由此可见，在粒子能量小于零的情况下，即在束缚态下只有当粒子能量取(10)式所给出的分立值时，波函数才有满足有限性条件的解.

结合能量本征值，合流超几何方程及其条件，得到氢原子的径向波函数为

(11)

(12)

由氢原子体系波函数的归一化条件

=1

及球谐函数Ylm(θ，φ)的归一化条件[15]，可知Rnl(r)的归一化条件为

(13)

将(11)式代入上式，可以算出径向波函数的归一化因子为

根据径向波函数公式(11)，我们得到前面几个径向波函数Rnl的表达式：

……

3 数值仿真

氢原子波函数的径向分布有几种表示方法：(1)径向波函数图，即波函数的径向部分Rnl对r作图；(2)径向波函数几率密度图，即Rnl2对r作图；(3)电子云的径向分布图，即径向分布函数D=r2Rnl2对r作图.下面通过MATLAB软件对其数值仿真，并加以讨论、分析.

3.1 径向波函数及其几率密度的数值仿真与讨论

结合式(11)和前面几个径向波函数的表达式，利用MATLAB软件，对氢原子的径向波函数及其几率密度进行数值计算，得到了16组径向波函数及其几率密度的仿真图，如图1和图2所示.

图1 氢原子的径向波函数的二维仿真图

由图1和图2可以看出，当r发生变化时，径向波函数及其几率密度也随之发生改变.当主量子数n越大时，原子轨道的最可几径向距离越大，则原子轨道的扩散程度越大；对单原子而言，当主量子数n相同时，角量子数l对原子轨道的径向分布影响不大，仅随角量子数l的增大，最可几径向距离稍有减小.

3.2 径向分布函数的数值仿真与讨论

尽管在量子力学中电子并无严格的轨道概念而只能给出位置的分布概率，但对于氢原子基态，量子力学给出的最可几半径r=a0(Bohr半径)可由数值仿真图的峰值给出.对于不同的主量子数n，角量子数l的值可以看出电子径向分布有不同的峰值，其代表了电子在此处出现的概率较大.

基于此，利用MATLAB软件，对氢原子的径向分布函数进行数值计算，得到了16组电子云的径向分布概率仿真图，如图3所示.

通过图3我们发现，曲线最高点的位置是D最大的球壳，且曲线波峰的数目等于n-l；任意两个及其以上波峰的图形中，两个相邻波峰之间必有一个零点，以零点的r为半径可作一球面，在此球面上电子云密度等于零，称为节面，且节面的数目等于n-l-1.如，图3中，图形(4)对于n=3，l=0态的氢原子在径向分布上有3-0-1=2个节面，图形(5)对于n=3，l=1态的氢原子在径向分布上有3-1-1=1个节面，图形(11)对于n=5，l=0态的氢原子在径向分布上有5-0-1=4个节面.

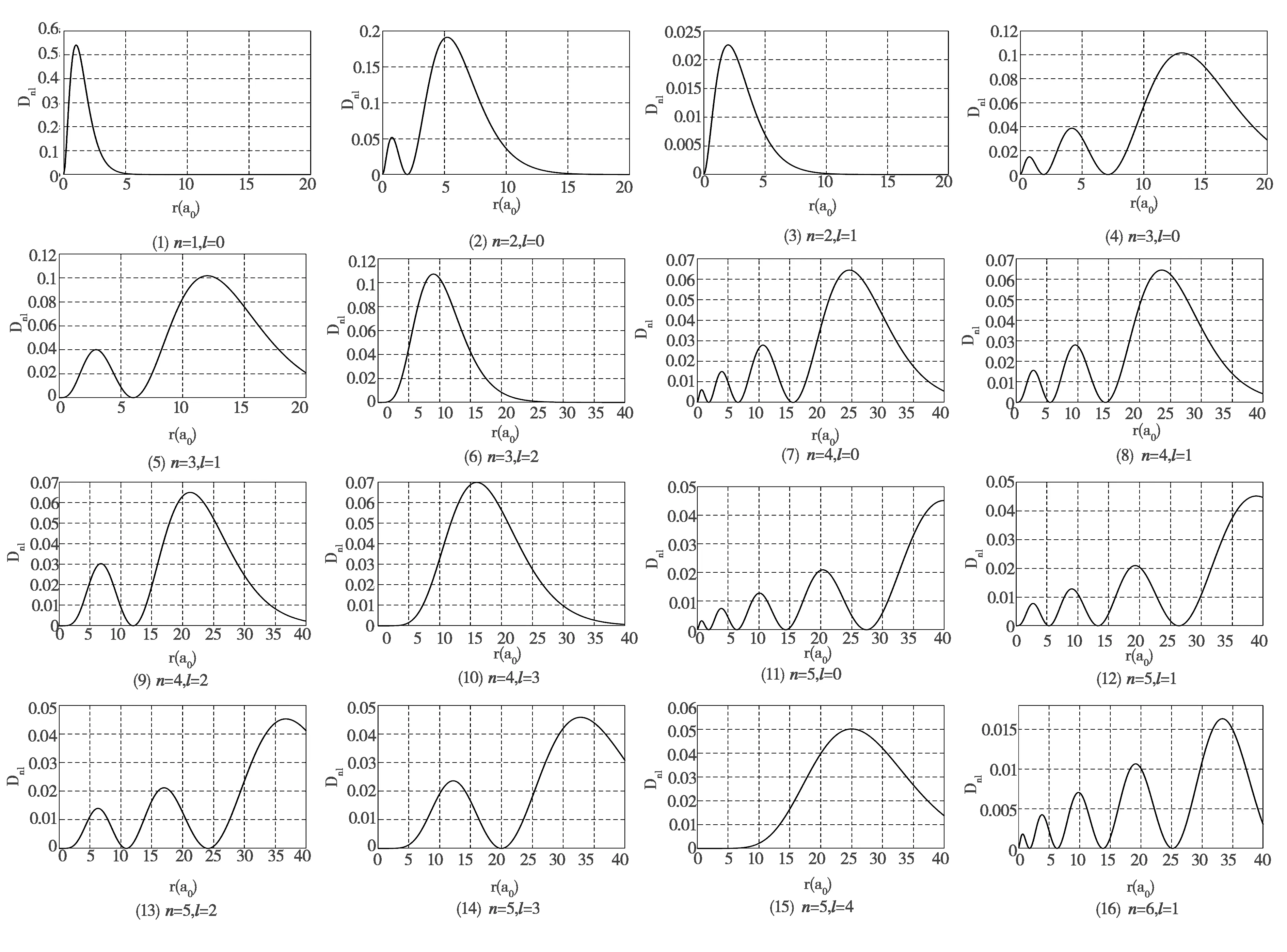
图3 氢原子径向分布函数的二维仿真图

总之，图中的峰值位置代表电子在此处出现的概率较大.这和旧量子力中的轨道概念有吻合之处.

3.3 能级简并的数值计算与讨论

电子的能级对m简并，即En与m无关，这是由于势场是中心力场(势能仅与r有关，而与n，φ无关)；能级对l简并，即En与l无关，则是库仑场所特有的.在碱金属原子中，价电子的势场也是中心力场，由于核体积较大，不是严格的库仑场.这样，价电子的能级Enl仅对m简并，对l则没有简并.

4 结论

本文在所学量子力学知识和数学物理方法的基础上，确定出氢原子体系的薛定谔本征方程及其径向和角向本征方程，通过分离变量法重点得出氢原子径向波函数的解析解.在以上工作的基础上，根据氢原子波函数的统计意义推导出了氢原子的径向波函数，并用MATLAB软件仿真绘制出氢原子径向波函数及其几率密度，电子空间分布函数的立体图，得到了可视化的结果.结果表明，当r发生变化时，径向分布几率密度也随之发生改变.当主量子数n越大时，原子轨道的最可几径向距离越大，则原子轨道的扩散程度越大；对单原子而言，当主量子数n相同时，角量子数l对原子轨道的径向分布影响不大，仅随角量子数l的增大，最可几径向距离稍有减小.分布函数曲线最高点的位置是D最大的球壳，且曲线波峰的数目等于n-l；任意两个及其以上波峰的图形中，任意两个相邻波峰之间必有一个零点，且节面的数目等于n-l-1.这种可视化的结果与理论推导的结果完全吻合，这对量子力学的学习具有重要的指导意义.