柔性互联配电网换流器控制模式平滑切换策略

王建建，孙凯祺，李可军，刘智杰，孙媛媛

（山东大学电气工程学院，山东省济南市 250061）

0 引言

随着分布式电源渗透率的不断提高以及负荷类型的多样化，传统的交流配电系统运行模式受到了挑战［1］。基于电力电子技术的柔性互联配电网可提高系统的控制灵活性和运行可靠性，将成为未来配电网的发展趋势［2-3］。但是高比例的可再生能源以及高比例的电力电子设备接入导致交流系统出现低短路比（short-circuit ratio，SCR）的弱电网特征，同时，可再生能源发电的波动性、发电机脱机以及负荷转供等工况造成系统的SCR 波动显著，对柔性互联配电网换流器的稳定、高效运行构成了挑战。

目前，柔性互联配电网中的换流器一般采用基于锁相环（phase-locked loop，PLL）［4］的电流矢量控制（current vector control，CVC）模式［5-6］。然而，弱电网下PLL 参数将严重影响系统的稳定性［7-8］。由于PLL 与电网阻抗之间存在耦合关系，且耦合关系会随着电网强度的减小及PLL 带宽的增大而加剧［9-10］。当系统SCR 小于1.3 时，基于电流矢量控制的换流器在额定工况下已难以维持稳定运行［10］。此外，弱电网下的PLL 会引入不对称正反馈环路［11］，将严重影响系统的稳定性，且PLL 的滞后效应还会对电流环产生不利影响，加剧换流器的静态稳定风险［12］。为提高电压源换流器（voltage source converter，VSC）向弱交流系统供电时的稳定性，文献［13］提出了功率同步控制（power synchronization control，PSC）策略。文献［14］则在此基础上加入了电流环，有效抑制了短路电流并增加了换流器的惯性支撑能力。功率同步控制以模仿同步电机的运行特性为基础，规避了向弱电网供电时PLL 引入的稳定性问题，更适用于与弱电网连接的换流器［15-17］。然而，当系统SCR 较大时，由于换流器采用功率同步控制后减小了系统的阻尼比，因此系统的稳定性会随着SCR 的增大而降低［18］。文献［19］通过对比功率同步控制及电流矢量控制在交流侧故障后的响应特性，建议SCR 大于1.4 时采用电流矢量控制，反之采用功率同步控制。

对于强度不断变化的交流系统，采用单一控制模式的换流器已无法满足系统的稳定运行需求。基于电流矢量控制与功率同步控制在不同电网强度下的特性差异，开展换流器多种控制模式的组合和切换研究，以实现交流系统强度大范围波动下的稳定控制非常必要。针对上述问题，文献［20］提出了一种电流源控制与电压源控制共存的双模式控制策略，实现了不同电网强度下的系统稳定运行，但针对2 种控制模式之间的切换策略及切换过程中可能产生的扰动并未深入研究。文献［21］针对交直流并联运行的场景，提出了一种电流矢量控制与电压-频率（V/f）控制的平滑切换策略。文献［22］为了提高换流器在不同故障工况下的运行稳定性，提出了电流矢量控制与功率同步控制的无扰动切换策略，但未考虑交流系统强度变化的运行工况。文献［23］针对并网换流器有功功率-无功功率（P/Q）控制模式与虚拟同步机控制模式切换问题，提出了一种基于控制器状态跟随的并行切换方法，但切换策略中的电流指令数值缓启动器会影响控制模式切换的快速性，且未考虑系统强度变化引入的扰动问题，同时其所采用的电流矢量控制无外环部分，仅能实现P/Q控制，无法实现其他控制方式，切换策略的通用性不足。文献［24］中提出了一种并网逆变器的虚拟同步机控制和P/Q控制的平滑切换方法，但该方法同样未考虑系统强度变化及通信延时的影响。

因此，考虑电流矢量控制与功率同步控制适用电网强度的不同，为使换流器能适应不同的系统运行工况，提升系统在不同电网强度下的运行稳定性，本文提出了一种电流矢量控制与功率同步控制间的平滑切换策略。首先，通过小扰动稳定和暂态稳定分析，揭示了功率同步控制和电流矢量控制在不同电网强度下的稳定性差异性；然后，分析了控制模式切换过程产生扰动的关键因素；最后，以抑制相位角及dq轴电流指令值的突变为目标，提出了一种电流矢量控制与功率同步控制方式间的平滑切换策略，并通过在功率同步环（power synchronization loop，PSL）增加功率前馈环节进一步减小了SCR 变化带来的扰动。

1 VSC 控制方式

1.1 电流矢量控制

电流矢量控制策略是以快速电流反馈为特征的直接电流控制策略，能够获得高品质的电流响应，在VSC 控 制 中 得 到 了 广 泛 应 用［19，25］。本 文 所 采 用 的电流矢量控制如图1 所示。图中，Pref和P分别为换流器输出有功功率指令值和实际值；vsm，ref和vsm分别为换流器输出交流电压幅值指令值和公共连接点（point of common coupling，PCC）处的交流电压幅值；vd、vq和id、iq分 别 为 交 流 电 压 和 电 流 的dq轴 分量；id，ref和iq，ref分 别 为d轴 和q轴 电 流 指 令 值；f0为 电网 额 定 频 率；Δf为 电 网 频 率 波 动；fpll和θpll分 别 为PLL 跟踪获得的电网频率和相位角；PI 为比例-积分控制器。

从图1 可知，该电流矢量控制共包含PLL 模块、外环控制器、内环控制器3 个部分。其中，PLL 模块主要用于跟踪电网电压相位，为坐标变换提供相位角基准。内环控制器跟踪dq轴电流指令值，实现对电流的控制，而外环控制器则通过跟踪有功功率、交流电压幅值等参考量获得dq轴电流指令值，最终与内环控制器形成串联，以实现换流器的控制目标。基于dq轴解耦特性，外环控制器能够针对有功类变量和无功类变量进行独立控制，除了图1 中所示的有功功率控制、交流电压幅值控制外，还可实现无功功率控制、直流电压控制、直流电压下垂控制等。这些控制器的组合共同构成了VSC 的基本控制方式。

图1 电流矢量控制示意图Fig.1 Schematic diagram of current vector control

1.2 功率同步控制

功率同步控制的核心思想是，基于同步发电机的摇摆方程进行换流器有功功率控制器设计，使得VSC 模拟同步发电机外特性，能够自主控制输出交流电压的频率和相位，而不是被动跟踪交流电网的频率和相位。同步发电机的摇摆方程为

式中:ω为实际电气角频率；ω0为电网额定角频率；δ为发电机功角；Pm为原动机机械功率；Pe为发电机电磁功率；TJ为发电机惯性时间常数；D为阻尼系数。

基于式（1），利用换流器输出功率指令Pref代替Pm，换流器实际功率P代替Pe，即可构造PSL 控制器，如图2 所示［13-14］。通过模拟同步发电机特性，PSL 可在控制换流器输出有功功率的同时产生相位角θpsl，是实现换流器与交流电网同步的关键。此外，功率同步控制还包括内环控制器和外环控制器，其中，内环控制器的设计与电流矢量控制完全相同，但功率同步控制的有功类变量控制是由PSL 完成。因此，外环控制器的设计与电流矢量控制有较大差异。外环控制器的d轴控制目标为跟踪交流电压指令 值vsm，ref，q轴 控 制 目 标 为 跟 踪q轴 电 压 指 令 值vq，ref，共同实现对换流器无功类变量的控制。与电流矢量控制类似，除图2 中所示的控制方式外，功率同步控制也可实现无功功率控制、直流电压控制、直流电压下垂控制等基本控制方式。

图2 功率同步控制示意图Fig.2 Schematic diagram of power synchronization control

2 电流矢量控制与功率同步控制稳定性对比

为了对比电流矢量控制与功率同步控制在不同电网强度下的小扰动稳定性及暂态稳定性特点，按照如附录A 图A1 所示的系统拓扑在PSCAD/EMTDC 中搭建了仿真模型。VSC 为模块化多电平换流器（modular multilevel converter，MMC），直流侧接直流电压源，与换流器相连的交流系统用戴维宁等效电路（理想电压源与系统阻抗Zs串联）表示［18］，通过改变Zs的大小模拟不同强度的交流系统，其中，Zs的阻抗角为50°。仿真模型相关参数如附录A 表A1 和表A2 所示。

2.1 小扰动稳定性对比

正常状态下换流器运行于逆变状态，采用P/V控制方式，交流电压幅值指令值为1.1 p.u.，有功功率指令值为1 p.u.（设换流器容量极限Smax=1.3，有功功率上限Pmax=1.2，无功功率上限Qmax=0.5）。附录A 图A2 和图A3 显示了5 s 时系统受到小扰动（负荷突增0.1 p.u.，持续时间为0.02 s）时，不同电网强度下换流器采用电流矢量控制和功率同步控制的仿真结果。从图中可知，若换流器采用电流矢量控制模式，在交流系统SCR 等于3 时，小扰动过后换流器输出的有功功率波动较小，且功率振荡衰减速度较快，有较强的稳定性。但随着系统强度逐渐减小，小扰动后换流器输出的有功功率波动幅度增大，且功率振荡衰减速度变缓，小扰动稳定性逐渐变差。与之相反，若换流器采用功率同步控制模式，则系统的小扰动稳定性会随着交流系统强度的增大而呈下降趋势。

2.2 暂态稳定性对比

附录A 图A4 和图A5 显示了5 s 时系统交流侧出现三相短路故障时（故障持续时间为0.1 s），不同电网强度下换流器采用电流矢量控制和功率同步控制的仿真结果。从图中可知，电流矢量控制模式下，当系统SCR 分别为3 和2 时，故障消除后换流器输出有功功率能快速上升并恢复稳定，换流器能够穿越交流侧三相短路故障，具有较好的暂态稳定性。但当系统SCR 下降至1.4 时，故障消除后换流器输出有功功率已无法恢复，出现了失稳现象。若换流器采用功率同步控制模式，则表现出了与电流矢量控制模式下相反的特性。当系统SCR 较小时，系统具有较强的暂态稳定性，但随着交流系统SCR 的持续增大，系统的暂态稳定性逐渐减弱，当SCR 增大至3 时，故障消除后换流器输出有功功率经3 s 振荡后仍未恢复稳定，系统的暂态稳定性已较差。

经对比分析可知，换流器所连交流系统的强度对系统的稳定性有显著影响，且换流器采用的控制模式不同，运行特性也不同。若换流器采用电流矢量控制，由于弱电网时PLL 会在基频附近引入负阻尼［26］，电网SCR 较大时，系统阻尼仍较大，但随着电网SCR 的减小，系统阻尼大幅度减小。因此，系统的小扰动稳定性和暂态稳定性均随电网强度减小呈下降趋势。若换流器采用功率同步控制，系统SCR较大时系统的阻尼较小，只有当系统SCR 较小时系统阻尼才会比较大［19］。因此，随着系统SCR 的增大，系统的小扰动稳定性和暂态稳定性均会逐渐降低。

综上所述，基于电流矢量控制与功率同步控制在不同电网强度下的稳定运行特性差异，当交流系统强度发生变化时，合理选择换流器的控制模式并实现不同控制模式之间的平滑切换以提高系统的稳定性，具有重要意义。

3 平滑切换策略

对于柔性互联配电网来说，正常运行工况下，交流系统的强度较为稳定。但当交流配电网中发生故障时，基于N-1 原则，故障线路被断开后联络开关将动作，以实现失电区域的负荷转供电，这将使得配电网拓扑结构发生变化，从而可能导致系统强度大幅度降低。此后，随着故障被清除，配电网拓扑恢复原状态，系统的强度也随之恢复。整个负荷转供电的过程将导致电网强度的大范围变化，这种情况下，单一的换流器控制策略已难以满足系统的稳定、灵活控制需求。为更好地适应系统的运行状态变化，结合电流矢量控制与功率同步控制的特点，使换流器在交流系统强度较大时能够运行于电流矢量控制中，强度较小时能够运行于功率同步控制中是一种可行的解决方案。但由于电流矢量控制与功率同步控制的原理不同，通常情况下，2 种控制模式间的直接切换将导致较大的扰动或无法成功切换。为实现2 种控制模式间的平滑切换，本文针对切换过程中造成扰动的关键因素进行了分析，并基于此提出了相应的控制模式平滑切换策略。

3.1 造成切换过程扰动的因素分析

稳态工况下换流器与交流系统的简化等效模型如附录A 图A6 所示［18］，由此可得换流器与交流系统间传输的功率为:

式 中:Q为 无 功 功 率；Vsvc和θsvc分 别 为PCC 处 交 流电压的幅值和相位角；E和θs分别为交流电源的电压幅值和相位角；Zs=Rs+jXs为系统的等效阻抗；α为系统阻抗角；Rs和Xs分别为交流系统等效阻抗的电阻分量和电抗分量。

对于同一系统，假设PLL 与PSL 处于并行状态，则当换流器运行于电流矢量控制模式时。由于PSL 控制器无法构成闭环，且积分器具有累积作用，则此时PSL 所输出的相位角θpsl与换流器当前控制目标下所需要的相位角并不相等。因此，θpll与θpsl之间存在差异，具体如附录A 图A7 所示。若换流器输出交流电压幅值不变，则切换前后换流器输出功率将存在差值，其差值大小可由式（3）推出。由式（3）可知，θpll与θpsl之间差值越大，则切换后功率的变化越大，从而导致切换过程中出现较大的功率波动。

式中:ΔP和ΔQ分别为有功功率和无功功率的波动。

通过对比功率同步控制与电流矢量控制的原理图可以发现，2 种控制模式下的内环控制器完全相同，因此，直接切换策略通过切换功率同步控制与电流矢量控制的dq轴电流指令值实现换流器在2 种控制模式间的切换。但正常运行状态下，换流器内有且仅有一种控制模式处于运行状态。因此，另一控制模式无法形成反馈回路，从而导致其输出的dq轴电流指令值与当前运行状态并不对应。若直接切换，则切换瞬间dq轴电流指令值存在突变，从而造成扰动，如附录A 图A8 和图A9 所示（SCR 为1.8，切换瞬间θ保持不变，5 s 时从电流矢量控制切换为功率同步控制，10 s 时切换回电流矢量控制）。

3.2 控制模式平滑切换策略

为了解决切换过程中θ突变造成的扰动问题，利用积分环节输出连续不突变的特性［27］，平滑切换策略对θ的跟踪环节进行了改进，如图3 所示。图中:Δω为角频率的波动。

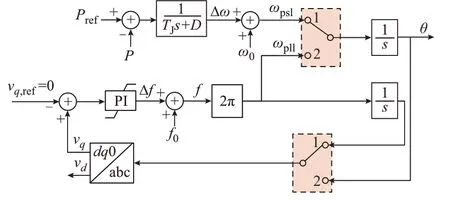
图3 相位角平滑切换框图Fig.3 Block diagram of smooth switching for phase angle

电流矢量控制模式下，切换开关处于位置2，此时，PLL 处于运行状态，θ=θpll。由于稳态运行情况下有P=Pref，因此PSL 获得的角频率有ωpsl=ω0。收到切换指令后，开关位置由2 变为1，换流器控制模式由电流矢量控制切换至功率同步控制。由于切换开关后存在积分器，且积分器输出具有连续不突变的特性，因此，切换瞬间的θ=θpsl=θpll，切换瞬间的θ无突变。由电流矢量控制向功率同步控制的切换完成后，开关处于1 位置时，此时PLL 与PSL 处于同步运行状态，由于PLL 具有跟踪电网相位的特点，功率同步控制模式运行期间，始终存在θpll=θpsl，且PLL 获得的角频率始终保持ωpll=ωpsl。因此，当切换开关由位置1 切换为位置2 时，换流器由功率同步控制切换为电流矢量控制，切换瞬间θ无突变。

为了解决切换过程中dq轴电流指令值突变造成的扰动问题，本文构造了如图4 所示的dq轴电流指 令 值 平 滑 切 换 结 构。图 中:id，cref和iq，cref分 别 为 电流 矢 量 控 制 下 的dq轴 电 流 指 令 值；id，pref和iq，pref分 别为功率同步控制下的dq轴电流指令值；vsm，pref和vq，sw，ref分别为电流矢量控制模式下功率同步控制外环的交流电压与q轴电压指令值；vsm，cref与Psw，ref分别为功率同步控制模式下电流矢量控制外环的交流电压与有功功率指令值。

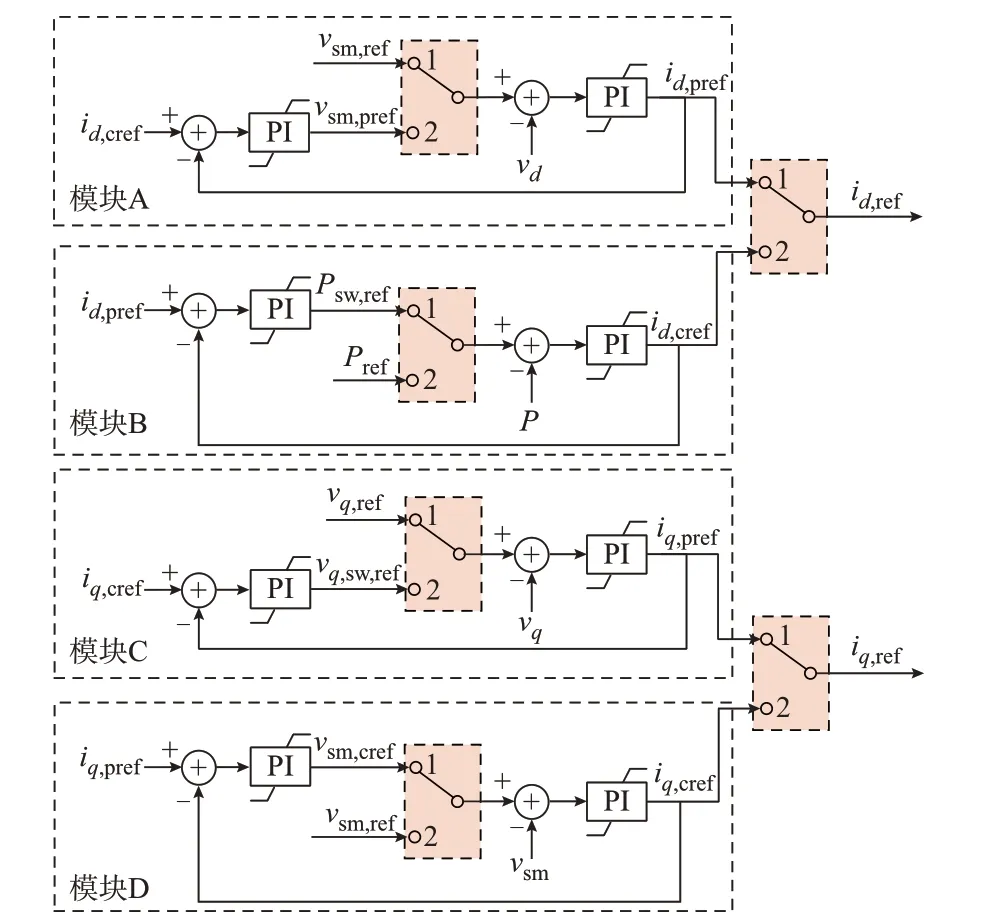
图4 dq 轴电流指令值平滑切换框图Fig.4 Block diagram of smooth switching for current reference value in dq axis

当图4 中的所有切换开关处于2 位置时，id，ref与模 块B 相 连，控 制 有 功 功 率P跟 踪Pref；iq，ref与 模 块D相连，控制交流电压幅值vsm跟踪vsm，ref，换流器处于电流矢量控制模式。同时，在电流矢量控制运行期间，模块A 和模块C 将独立运行，实现功率同步控制输出的dq轴电流指令值与电流矢量控制输出的dq轴 电 流 指 令 值 之 间 的 同 步，即 让id，pref、iq，pref跟 踪id，cref和iq，cref，最 终 使 得id，pref=id，cref，iq，pref=iq，cref。当 图4中 的 所 有 切 换 开 关 处 于 位 置1 时，id，ref与 模 块A 相连，控 制d轴 电 压vd跟 踪vsm，ref；iq，ref与 模 块C 相 连，控制q轴电压vq跟踪vq，ref，换流器处于功率同步控制模式。此时，模块B 和模块D 将独立运行，实现电流矢量控制输出的dq轴电流指令值与功率同步控制输出的dq轴电流指令值之间的同步，即让id，cref、iq，cref跟 踪id，pref和iq，pref，最 终 使 得id，cref=id，pref，iq，cref=iq，pref。通 过 对2 种 控 制 模 式 间dq电 流 指 令 值的同步，当换流器的控制模式进行切换时，无论切换开关位置从1 切换为2，还是从2 切换为1，在切换瞬间 始 终 有id，cref=id，pref，iq，cref=iq，pref。因 此，id，ref与iq，ref在切换瞬间将保持不变，从而解决了切换过程中dq轴电流指令值突变引入的扰动问题。

除 切 换 过 程 中θ与id，ref、iq，ref突 变 造 成 的 内 部 扰动外，若在交流系统SCR 变化的同时进行控制模式切换，则SCR 的变化也会为系统带来一定的外部扰动。由式（2）可知，换流器与交流系统间传输的功率与系统的等效阻抗相关，根据SCR 的定义可知，等效阻抗的模与系统SCR 成反比关系。因此，系统SCR 的变化必将导致|Zs|发生变化，从而使换流器输出功率出现波动。为使功率恢复原值，在PCC 处电压不变的情况下，则必须要改变PCC 处电压相位。然而，当换流器由电流矢量控制切换为功率同步控制后，其输出电角度θ仍为SCR 变化前所需电角度θSCR1，为了达到稳态，必须逐渐变化至当前SCR 下所需电角度θSCR2，该动态过程的变化速度与其引起的功率波动大小由功率同步控制的惯性与阻尼环节决定。为了不改变控制系统的参数而影响换流器在其他工况下的运行性能，同时减小该动态过程中功率的最大变化量、加快动态响应速度，在控制模式切换过程中引入功率前馈环节，如图5 所示。图中:K为常数；kint为积分环节增益。

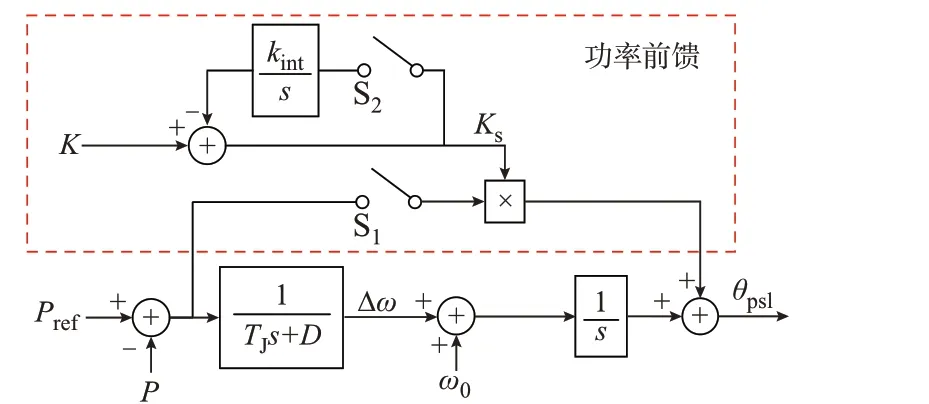
图5 功率前馈Fig.5 Power feedforward

正常情况下，开关S1和S2处于开通状态，当换流器接收到由电流矢量控制向功率同步控制进行切换的信号后，开关S1和S2闭合，从而在PSL 环节增加一个功率前馈环节，加快θ的变化。当Ks≤ε时，开关S1和S2打开并将积分环节复位，功率前馈环节退出运行。ε为功率前馈环节退出运行的判据。需要说明的是，虽然本文所提出的换流器控制模式平滑切换策略是以P/V控制方式为例进行设计，但该平滑切换策略的原理对于P/Q控制等其他换流器控制方式下的控制模式平滑切换同样适用。

4 平滑切换策略验证分析

4.1 稳态切换

为验证系统强度不变的稳态运行情况下，控制模式平滑切换策略的有效性，基于附录A 图A1 在PSCAD/EMTDC 中搭建了对应的仿真模型，对控制模式平滑切换策略与直接切换策略进行了效果对比。直接切换策略的原则是:不考虑平滑切换措施，在θ以及id，ref、iq，ref处直接切换。其中，仿真模型参数见附录A 表A1 和表A2。

假设交流系统SCR 为1.8，换流器于5 s 时从电流矢量控制切换至功率同步控制，10 s 时从功率同步控制切换回电流矢量控制，采用直接切换策略与平滑切换策略下，VSC 输出有功功率、交流端电压及θ与id，ref、iq，ref的 变 化 情 况 如 图6 所 示。从 图 中 可知，平滑切换策略下，无论是电流矢量控制向功率同步控制切换还是其逆过程，在切换瞬间，θ与dq轴电流指令值均未产生突变，换流器输出有功功率的最大变化量约为原值的3.6%，而交流端电压波形在切换前后几乎无变化，切换过程十分平滑。在直接切换策略下，当电流矢量控制向功率同步控制切换时，由于θpll与θpsl之间以及2 种运行模式下dq轴电流指令值的差异性，导致在切换瞬间的θ与id，ref、iq，ref均存在明显突变；当功率同步控制向电流矢量控制切换时，虽然切换瞬间的θ不存在突变，但id，ref、iq，ref仍有明显突变。因此，在直接切换策略下，2 种控制模式间的切换过程导致换流器输出有功功率及交流端电压波形均出现了较大波动。由上述分析可知，在交流系统强度不变的情况下，在电流矢量控制与功率同步控制的切换过程中，平滑切换策略均未造成任何扰动，验证了平滑切换策略的有效性和正确性。

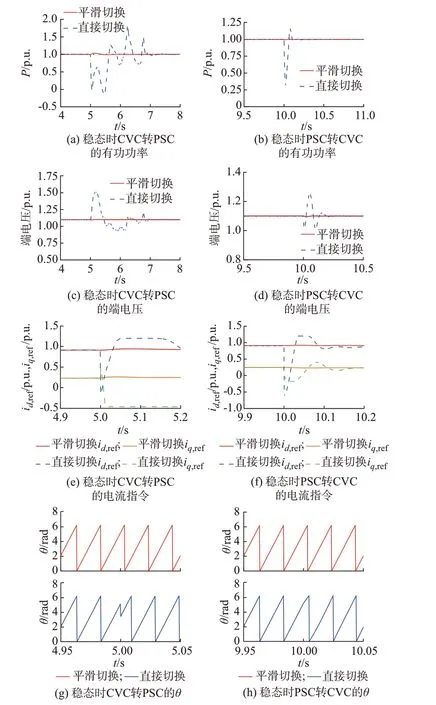
图6 稳态时换流器控制模式切换响应Fig.6 Switching response of converter control mode in steady state

4.2 电网强度变化下切换

配电网中，基于N-1 原则的负荷转供电策略将导致系统的SCR 发生大范围变化。因此，为保证系统运行的稳定性，考虑在系统SCR 变化时，对换流器的控制模式进行切换。根据附录A 图A2 至图A5 的仿真结果可知，当交流系统SCR 不大于1.4时，电流矢量控制已无法在故障后恢复稳定运行；当交流系统SCR 不小于3.0 时，功率同步控制模式下的换流器输出功率在故障消除后出现了较长时间且较大幅度的振荡。因此，本文中将选择交流系统SCR 为1.5 和3.0 时作为2 种控制模式间的切换边界，构成如附录A 图A10 所示的滞环切换回路，以减少非必要情况下的控制模式频繁切换。

基于图7 所示的柔性互联配电网拓扑结构在PSCAD/EMTDC 中搭建仿真模型，换流器各参数参照附录A 表A1 和表A2 所示。其中，交流系统1和交流系统2 的额定电压均为10 kV（IEEE 33 节点算例）［28］，换流器1 和2 完全相同，换流器2 采用定直流电压控制，换流器1 采用P/V控制。初始状态下，交流系统1 的SCR 为3.53，换流器运行于电流矢量控制模式，5 s 时线路29-30 因故障被断开，为向失电区负荷进行转供电，线路18-33 间的联络开关闭合，交流系统1 的SCR 瞬间下降为1.37。由于此时SCR 小于1.50，换流器控制模式将由电流矢量控制切换为功率同步控制。运行一段时间后，在10 s 时故障被清除，线路18-33 间的联络开关断开，线路29-30 恢复运行，交流系统1 的SCR 恢复。此时，SCR 恢复至3.53，换流器控制模式切换回电流矢量控制。由于整个切换过程中需通过检测当前系统中联络开关的状态，并根据事先构造的联络开关不同状态下交流系统SCR 集合判断换流器控制模式是否需要切换，从而发送切换信号，考虑到联络开关的状态检测、信号传输、切换指令判定等均需一定的时间，因此，本文中将考虑20 ms 的通信延迟。

图7 双端柔性互联系统结构图Fig.7 Structure diagram of two-terminal flexible interconnected system

直接切换策略、完整平滑切换策略及无功率前馈环节的平滑切换策略下VSC1 输出有功功率、交流 端 电 压 及θ、id，ref、iq，ref的 响 应 结 果 如 图8 所 示。从图 中 可 知，在 直 接 切 换 策 略 下，因id，ref和iq，ref在 切 换瞬间的突变、SCR 变化带来的影响及θ在电流矢量控制切换为功率同步控制瞬间的突变，在电流矢量控制向功率同步控制切换时出现了较大的有功功率波动以及过电压，且dq轴电流指令值达到了限值，控制模式切换失败。同时，在功率同步控制向电流矢量控制切换时，换流器输出有功功率及交流端电压曲线也出现了较大波动。相比之下，平滑切换策略 因抑 制 了θ与id，ref、iq，ref在 切 换 瞬 间 的 突 变，在2 种控制模式的切换过程中，换流器输出有功功率及交流端电压曲线更为平缓，实现了2 种控制模式间的平滑切换。同时，在换流器由电流矢量控制向功率同步控制切换时，引入功率前馈环节后，切换过程中的有功功率波动幅值大幅度下降，最大幅值由0.726 9 p.u.下降至0.666 2 p.u.，有效削弱了SCR 变化所带来的扰动。

图8 SCR 变化下换流器控制模式切换响应Fig.8 Response of converter control mode switching with changing SCRs

图9 为换流器分别采用本文提出的控制模式平滑切换策略、文献［23］提出的基于控制器状态跟随的并行切换方法的仿真结果。由图9 可知，在换流器由功率同步控制向电流矢量控制切换的过程中，2 种切换策略下的系统响应均较平稳；在换流器由电流矢量控制切换至功率同步控制的过程中，采用本文所提平滑切换策略后，有功功率最大波动量为0.066 2 p.u.，交流端电压最大波动量为0.033 8 p.u.，而在采用基于控制器状态跟随的并行切换控制策略下，切换过程中的功率和电压波动相对较大，有功功率的最大波动量为0.168 5 p.u.，交流端电压最大波动量为0.066 0 p.u.。

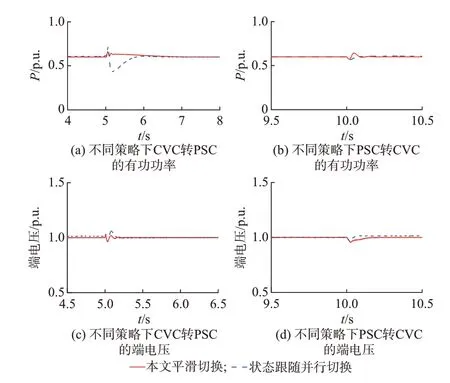
图9 SCR 变换下不同切换控制策略响应Fig.9 Response of different switching control strategies with changing SCRs

5 结语

为适应柔性互联配电网不同运行工况下的控制需求，充分发挥电流矢量控制与功率同步控制在不同电网强度下的优势，通过抑制电网相位角θ及id，ref、iq，ref在 切 换 瞬 间 的 突 变，本 文 提 出 了 一 种 电 流矢量控制与功率同步控制间的平滑切换策略，提升了系统对复杂工况的适应性。

1）随着交流系统强度的降低，电流矢量控制方式下的系统小扰动及暂态稳定性均呈下降趋势，而由于控制原理的不同，功率同步控制下的系统小扰动及暂态稳定性随交流系统强度变化的特性与电流矢量控制存在较大差异。

2）电网相位角θ与dq轴电流指令值在切换瞬间的突变以及SCR 的变化是造成控制模式切换时出现扰动的主要因素。

3）所提出的平滑切换策略可实现在交流系统强度变化时电流矢量控制模式与功率同步控制模式间的无扰动切换，与直接切换相比拥有更平滑的切换效果，同时可以削弱SCR 变化带来的扰动。

本文所提方法暂未考虑柔性互联配电网两侧换流器均需切换的场景。在后续工作中仍需考虑更加复杂的切换场景，并在此基础上对换流器的控制模式切换策略进行改进和完善。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。