内部带阻尼格栅的TLD减振性能试验研究

张蓝方，张乐乐，谢壮宁，江 毅

（1.华南理工大学亚热带建筑科学国家重点实验室，广东广州 510640；2.华南理工大学建筑设计研究院有限公司，广东广州 510640）

引言

近年来，超高层建筑的设计越来越倾向于更轻、更柔，其对风致振动更加敏感。不少建筑的结构顶部峰值加速度在《高层建筑混凝土结构设计技术规程》规定的10年重现期风作用下仍相对偏高，对峰值加速度的控制成了结构抗风设计的重要问题，并会进一步影响造价。

动力减振器（DVA）是一种常用在超高层建筑风振控制中的被动控制装置，将该装置的频率调谐至与结构频率相近以起到吸振控制作用。调谐质量阻尼器和调谐液体阻尼器（TLD）是两种常用于超高层风振控制的DVA［1-4］。其中，TLD 因构造相对简单、造价低，且可兼做消防水箱而受到越来越多的关注。TLD 的频率和阻尼比是与其减振性能相关的两个重要性能参数。TLD 频率与其构造尺寸、液深有关，而TLD 阻尼主要来自于自由液面破碎、液体黏度以及液体与水箱壁面的摩擦［5］。仅依靠上述几种耗能方式，TLD 所能提供的阻尼比远小于最优值，难以达到有效控制结构风致振动的效果，因此需要采取增大液体晃荡耗能的措施，包括增加水箱壁面粗糙度、在TLD 内设置耗能装置如阻尼网、格栅等，而增设耗能装置后包括系统的模态频率、阻尼和振型在内的TLD 固有特性是TLD 设计所关注的重要问题。

TLD 中液体晃动过程分析可采用理论分析、振动台试验和数值模拟方法［6-8］。基于线性波浪理论可以获得简单平面形式（矩形和圆型）TLD 液体晃动频率和有无格栅时的模态阻尼比，TLD 液体晃动会呈明显非线性特征［6］，其性能参数的获取更多地是采用振动台试验方法［7］。振动台试验则通常采用扫频方法获得液面峰值波高随频率变化曲线，进而确定TLD 频率和等效阻尼比，但扫频方法需要进行多条不同频率正弦波激励加载，费时费力；同时扫频方法本质上是针对物理坐标系响应的直接识别方法、不能准确识别可能存在耦合系统的模态参数。故需要采用更为经济、高效、可靠的方法来研究TLD 性能参数。

针对以上问题，本文采用一种基于有色噪声激励的水箱特性振动台试验方法，对测得的水箱液面多点响应信号进行解耦分离，再采用不同识别方法进行参数识别。对内部带阻尼格栅的矩形水箱的减振性能进行了详细的试验研究，分析了格栅位置、稠度比和相对激励幅值对水箱自振频率和模态阻尼比的影响并和基于线性理论的计算结果进行对比，验证所用方法的有效性和结果的可靠性。

1 TLD 振动台试验

1.1 试验模型

TLD 试验模型尺寸如图1所示，其中无阻尼格栅TLD（图1（a））为带阻尼格栅TLD（图1（b））的试验对比组。TLD 模型净空尺寸L×B×h（长×宽×液深）为2.1 m×0.64 m×0.44 m，采用钢板和PC 板制作，假定缩尺比为1∶10，各变量相似准则［9］如表1所示。阻尼格栅共有两块，为不锈钢材质，如图1（c）所示，每块格栅的宽度l为0.64 m，高度b为0.7 m，厚度为0.002 m。格栅的疏密程度用稠度比S来表示：

表1 相似准则Tab.1 Similitude law

图1 TLD 模型尺寸Fig.1 Model sizes of TLD

式中As为格栅实心部分面积，AT为格栅总面积。

1.2 试验装置和施加激励

TLD 试验模型如图2所示，考虑到扫频方法效率低下的缺点，本文采用基于有色噪声激励的振动台试验方法来研究带阻尼格栅TLD 的减振性能，试验装置如图3所示。试验采用4 个数字波高计来测量TLD 内液体沿长边方向的自由表面高度（即波高）变化情况，采样频率为100 Hz，并采用加速度传感器测量振动台台面加速度，采样频率为25 Hz。为避免前一工况对后一工况试验结果的影响，每个工况均待TLD 响应平稳后开始采样，采样时长为5 min。

图2 TLD 试验模型Fig.2 Test models of TLD

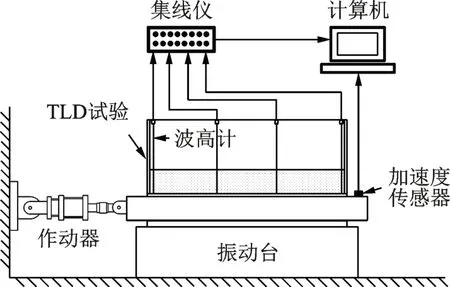
图3 试验装置示意图Fig.3 Schematic of test apparatus

试验所使用振动台为Servotest 公司生产的3 向6 自由度地震模拟振动台，该振动台系统加载模式为位移加载，不能直接对试验试件施加加速度激励，因此本文根据位移谱和加速度谱的关系，采用等效位移谱模拟生成的位移时程作为振动台系统所施加的激励，并沿着TLD 试验模型长边方向进行单向加载。

假定在有色噪声带宽范围内，所施加位移激励功率谱为频率f的指数函数，则位移激励功率谱可表示为：

式中α和β为由测试系统即振动台装置的加载方式所决定的系数，本试验为位移加载模式，故α=2π，β=-4；a和b为有色噪声带宽范围的下限和上限，根据试验水箱液体晃动频率的大致范围，取a=0.2 Hz，b=3 Hz。采用随机模拟方法［10-11］将频域表达的位移激励功率谱SFF(f)转化为时域表达的位移激励时程x(t)，如下式所示：

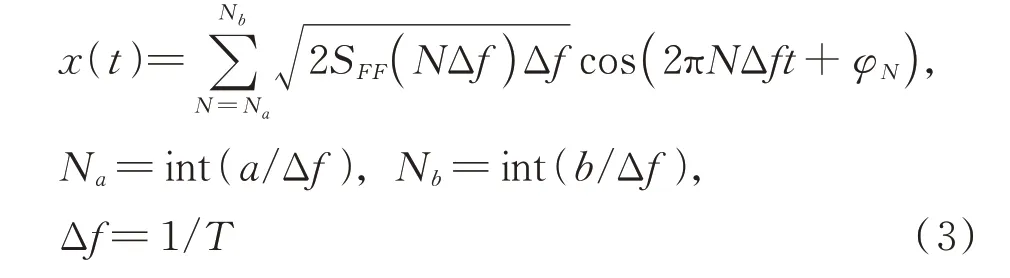
式中 Δf为离散频率点的频率间隔，φN为在［0，2π］区间内满足均匀分布的随机相位角，N为离散化的位移激励功率谱线序列，T为要模拟的样本时间。采用上述方法进行模拟得到位移激励的模拟结果如图4（a）所示，图4（b）为相应的功率谱密度，由图可见模拟的位移谱和目标谱吻合良好。

图4 位移激励Fig.4 Displacement excitation

对位移激励时程求两次导数得相应的加速度激励时程，如图5所示。图5 表明在0.2～3 Hz 频率范围内，所施加激励的谱为白噪声谱。

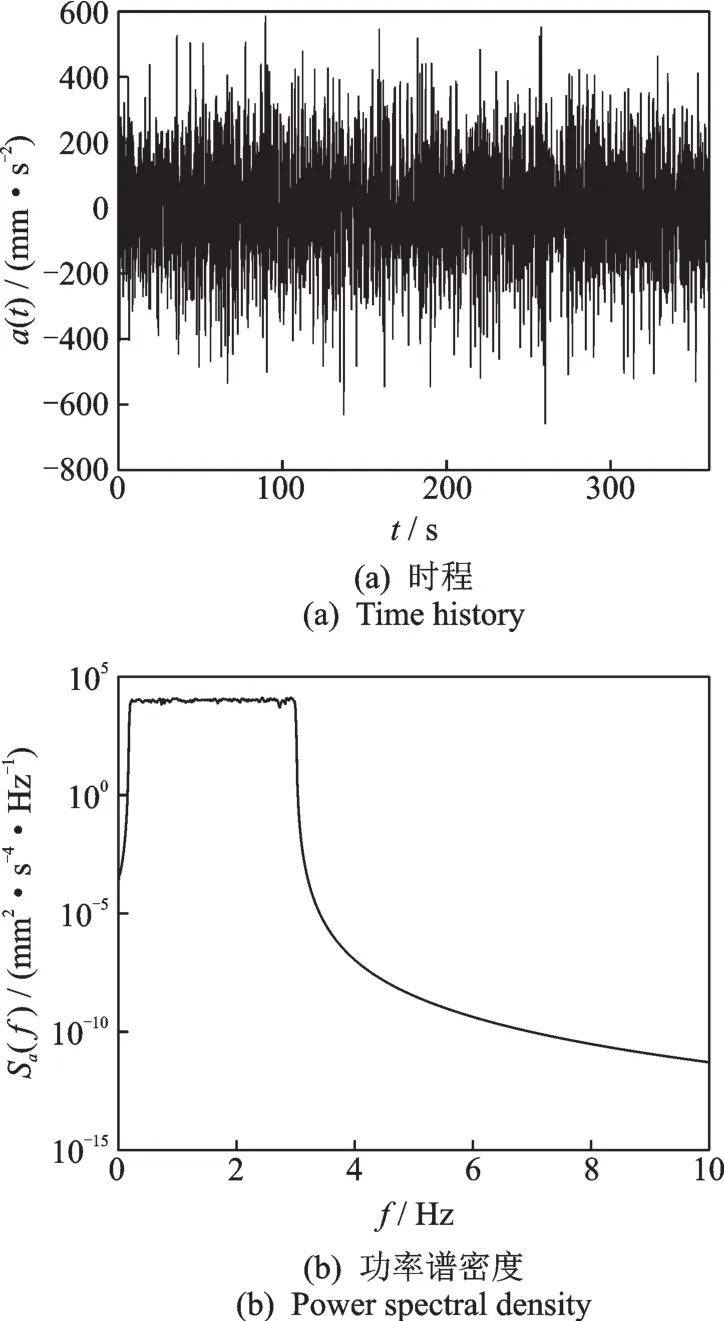
图5 加速度激励Fig.5 Acceleration excitation

1.3 试验工况

为研究带阻尼格栅TLD 的减振性能进行了一系列试验，具体试验工况如表2所示。对随机模拟方法生成的位移激励进行调幅，并用Λ=σe/L来衡量激励相对幅值的大小，σe为位移激励时程均方根值。

表2 试验工况Tab.2 Test cases

1.4 TLD 性能参数理论解

基于线性波浪理论可以得到典型平面形状的TLD 固有特性。对于矩形平面水箱，其液体晃荡的第j阶频率为［12］：

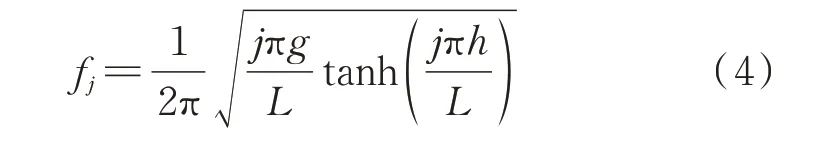
式中L为水箱沿液体晃荡方向长度（如图1（a）），h为TLD 内液体深度，g为重力加速度。无阻尼格栅TLD仅通过液体的黏度耗散能量，所产生的阻尼比ςw为［13］：

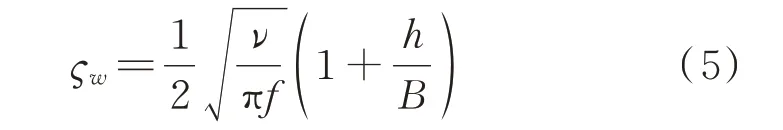
式中ν为液体的运动黏度，B为TLD 宽度。有格栅时的阻尼比与激励幅值和激励类型有关，当激励类型为白噪声时，阻尼格栅的理论阻尼比ςs为［14］：

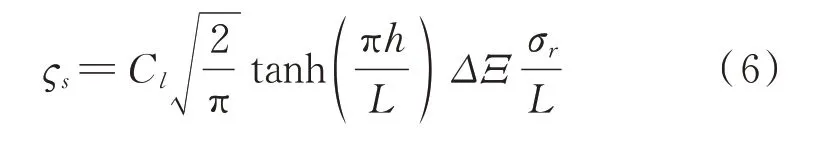
其中，

式中σr为流体晃动响应的均方根值，ns为TLD 内部设置的阻尼格栅数量，xk为第k个格栅到水箱左侧壁面的距离，Cl为与格栅稠度比S有关的损失系数。

1.5 TLD 性能参数识别方法

在进行TLD 性能参数识别前，本文采用复数形式的二阶盲辨识（SOBI）方法［15］对波高计测得的TLD耦合响应信号进行解耦。该方法先对TLD 耦合响应信号进行复数化，再将复信号白化，对白化信号的延时相关矩阵进行联合对角化逼近，进而求得TLD 的复振型矩阵与复分离矩阵，最后由复分离矩阵计算得到解耦后的各阶模态响应信号：

对于解耦后的模态响应信号，进行TLD 性能参数识别，以求得TLD 频率和阻尼比。参数识别方法采用改进贝叶斯谱密度法（MBSDA）和曲线拟合法。其中，MBSDA 方法［16］假设模态坐标下激励的功率谱密度函数为：

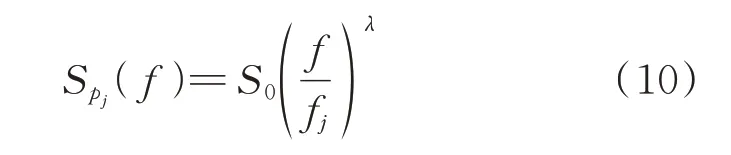
式中S0为输入激励在TLD 固有频率处的功率谱密度值，λ为激励幂指数。这使得MBSDA 方法既可适用于白噪声激励，又可适用于有色噪声激励的情况。对于平稳过程，在特定频率区段内，TLD 响应功率谱密度的概率分布可近似为Chi-square 分布，该分布可采用含有TLD 性能参数的函数来表示，通过令TLD 性能参数的后验概率密度函数最大化，使求得的参数结果达到最优。参数识别结果的不确定性通过后验变异系数（标准差除以最优解）来评估。

曲线拟合方法与MBSDA 方法采用相同的模态激励功率谱密度函数假设，解耦后的模态响应信号和模态激励的功率谱密度的关系为：

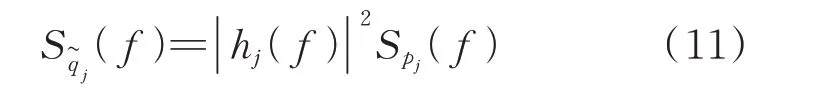
2 试验结果分析

2.1 无阻尼格栅

分别在Λ=0.0012，0.0018，0.003 三种不同相对激励幅值作用下，进行无阻尼格栅TLD 振动台试验，对试验测得的TLD 中液面波高信号进行模态解耦后再分别采用MBSDA 方法和曲线拟合法进行参数识别，得到S0，λ，TLD 频率fj和阻尼比ζj。将参数识别结果代入式（10）和（11），在TLD 一阶模态频率附近，得到无阻尼格栅TLD 的试验结果与参数识别结果对比如图6所示。

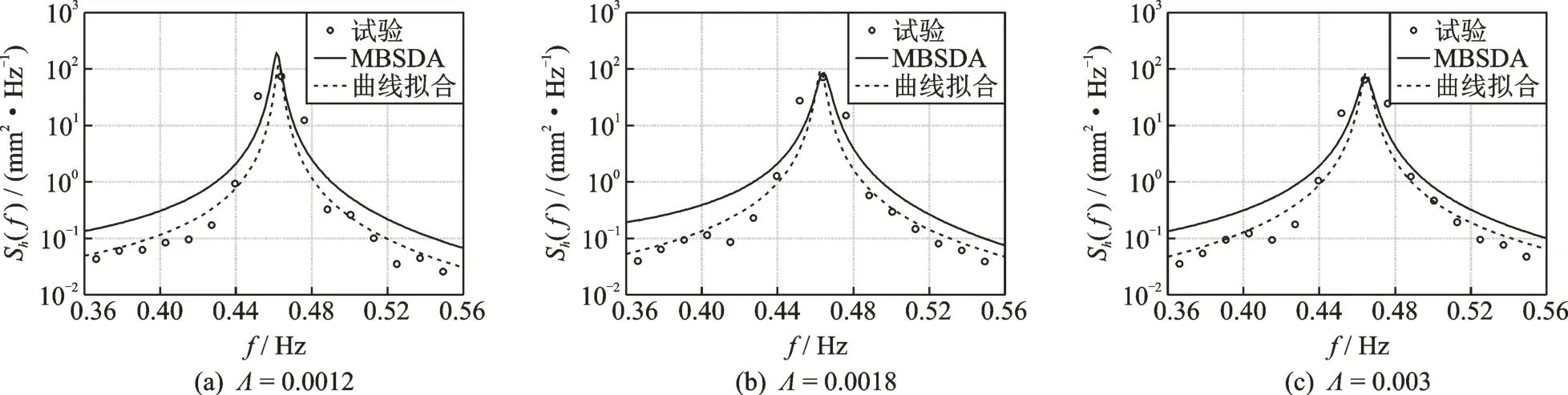
图6 试验结果与参数识别结果比对Fig.6 Comparison of test results and parameter identification results

由图可知，在白噪声激励作用下，液面波高功率谱密度曲线与线性系统响应谱曲线明显不同，液面波高功率谱曲线呈现明显非线性特征，这种特征出现在后续所有试验结果中。采用线性化方法对试验结果进行分析可知，MBSDA 方法和基于最小二乘法的曲线拟合方法的识别结果存在差异，其原因在于MBSDA 方法偏向于关注峰值局部偏差大小，而曲线拟合法则更强调控制整体偏差的大小。根据式（4）计算内部未设置阻尼格栅TLD 一阶模态频率的理论值为0.46 Hz，由图可知频率识别结果与理论值吻合较好，说明两种方法识别频率的准确性。且TLD 频率随相对激励幅值Λ增加无明显变化。

无阻尼格栅TLD 试验阻尼比识别结果与相对激励幅值Λ，相对响应σr/L的关系分别如图7（a）和（b）所示，理论值根据式（5）计算得到。由图可见一阶模态阻尼比的试验识别结果大于理论值，这是由于理论值只考虑了液体黏度对阻尼的贡献，未考虑TLD 试验模型内部壁面摩擦对阻尼的增大作用。MBSDA 方法识别阻尼比大于曲线拟合方法，且识别结果分别随Λ，σr/L增加而略增大。

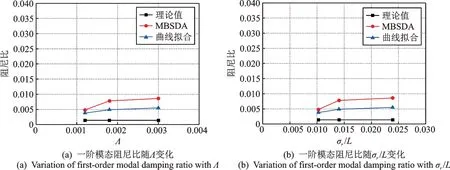
图7 一阶模态阻尼比识别结果与理论值比对Fig.7 Comparison of first order damping ratio identification results with theoretical values

2.2 阻尼格栅的影响

对带阻尼格栅的TLD 进行了3 组不同试验，分别研究不同稠度比（S=0.33，0.42，0.55，0.64，0.76）、格栅设置位置（xk/L=0.4 & 0.6，0.3 & 0.7，0.25 & 0.75）、相对激励幅值（Λ=0.0012，0.0018，0.003，0.0042，0.0054，0.006）对TLD减振性能的影响。图8 给出部分工况一阶模态功率谱密度的试验结果与参数识别结果的对比。由图可知参数识别结果与试验结果吻合良好，说明两种参数识别方法的可靠性。与图6 相比可知，带阻尼格栅TLD 一阶模态频率无明显变化，说明在TLD 内设置阻尼格栅不会改变TLD 一阶模态频率，且频率不随相对激励幅值变化而改变。

图8 试验结果与参数识别结果比对Fig.8 Comparison of test results and parameter identification results

首先考虑稠度比S对TLD 一阶模态阻尼的影响，取xk/L=0.4 & 0.6，Λ=0.003，参数识别结果如图9所示。由图可见，在TLD 中设置格栅能够增大一阶模态阻尼比，且阻尼比随S增加而增大。在本组参数下，两种不同参数识别方法得到的模态阻尼比较为接近，当S＜0.5 时，参数识别结果略大于理论值；当S＞0.5 时，参数识别结果小于理论值且两者的差别随S的增大而增大。

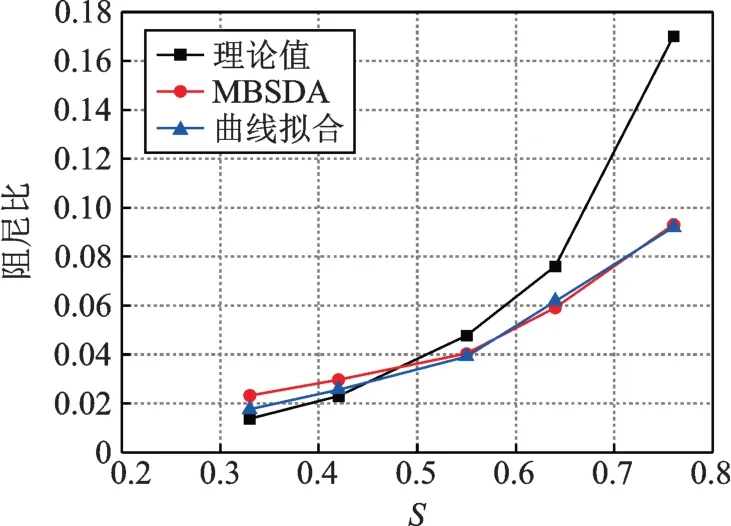
图9 一阶模态阻尼比随稠度比S 变化（Λ=0.003）Fig.9 Variation of first-order modal damping ratio with solidity ratio S（Λ=0.003）

进一步考虑相对激励幅值Λ对一阶模态阻尼比的影响（固定取xk/L=0.4 & 0.6，S=0.42），参数识别结果如图10（a）所示。阻尼比与相对响应的关系如图10（b）所示。由图可见，阻尼比有分别随的增大而增大的趋势，且当Λ≥0.003，时，两种识别方法得到的结果和理论结果较为接近；在时，两种方法的结果均大于理论值，且MBSDA 得到的结果最大，采用理论值可能会低估TLD 的阻尼值。

图10 一阶模态阻尼比识别结果与理论值比对Fig.10 Comparison of the identified first order damping ratio with theoretical values

在S=0.42，Λ=0.003 时，考察格栅位置对液体晃动的模态阻尼比的影响结果如图11所示。图中同时给出前两阶模态阻尼比随格栅相对位置变化的影响。由图可见，随着格栅设置位置靠近二阶振型，一阶模态阻尼比减小，二阶模态阻尼比增大。

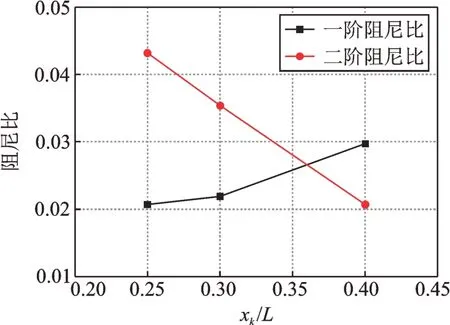
图11 TLD 阻尼比与格栅设置位置的关系Fig.11 Relationship between TLD damping ratio and the screen position

下面结合图12 和液面速度的晃动模态说明以上影响规律。图12 为采用线性波浪理论计算的前两阶模态的归一化速度幅值Ω沿TLD 长边方向变化曲线。当格栅位置处于xk/L=0.4 & 0.6 时，一阶模态归一化速度幅值Ω大于二阶模态，随着格栅位置变化，一阶模态Ω变小，二阶模态Ω变大，当格栅位置处于xk/L=0.25 & 0.75 时，一阶模态Ω小于二阶模态，格栅上的压力损失与速度的平方成正比，因此随着格栅位置变化，阻尼格栅对一阶模态的抑制作用变小，对二阶模态的抑制作用变大。

图12 前两阶归一化流体速度与TLD 中阻尼格栅的位置Fig.12 The first two order normalized fluid velocity and the positions of damping screens in TLD

3 结论

由本文研究可得以下结论：

（1）采用基于有色噪声激励下的水箱特性振动台试验方法、复二阶盲辨识信号分离和多种参数识别方法校核能够快速地获得可靠的TLD减振性能参数。

（2）在TLD 内设置阻尼格栅不改变TLD 频率，但能增加TLD 阻尼比，且TLD 一阶模态阻尼比随稠度S比增加而增大，当S＜0.5 时，参数识别结果略大于理论值；当S＞0.5 时，参数识别结果小于理论值且两者的差别随S的增大而增大。

（3）TLD 一阶阻尼比有分别随相对激励幅值、相对响应的增大而增大的趋势，且当0.006时，采用理论值可能会低估TLD 的阻尼值。

（4）TLD 中阻尼格栅设置位置对TLD 各阶模态阻尼比大小有影响，随着格栅设置位置靠近二阶振型，一阶模态阻尼比减小，二阶模态阻尼比增大，有助于抑制非线性响应，从而提高TLD 的可控性与可靠性。