轻钢桁架龙骨外墙挂板抗弯刚度分析及试验研究

陈英杰 董睿成，* 陈国新 杨 桓

（1.新疆农业大学水利与土木工程学院，乌鲁木齐 830052；2.新疆建筑科学研究院（有限责任公司），乌鲁木齐 830000）

0 引 言

我国的经济建设高速发展，人们对美好生活具有更高的向往，对建筑产业的节能、环保以及高效的需求日益增加，在这种环境下装配式钢结构住宅得到广泛的认可和应用。装配式钢结构住宅建筑，其抗震性能好，节约建筑材料，施工阶段更符合环保要求，大部分采用干法施工可以有效降低场地的噪音，扬尘等污染[1]。但同时钢结构住宅为保证建筑的节能保温性能以及墙板的实用性，要求围护体系具有保温节能性能的同时也具有易于安装转运的特点[2]。对于外墙挂板的研究中，肖建庄[3]、李学稼[4]、魏光耀[5]、刘伟[6]等对混凝土结构外挂墙板的连接件及连接性能进行了试验分析以及理论研究等一系列工作，分析不同结构的墙体其连接件的力学性能以及采用不同连接件对墙板受力性能的影响。谢剑[7]、黄远[8]、李悦[9]、杨超望等[10]对混凝土结构外墙挂板的抗震性能以及墙板对建筑的抗震贡献进行研究，确定了地震作用下外挂墙板的可靠性以及外墙挂板对剪力墙抗侧刚度的影响因素。可见国内研究对外挂墙板自身抗弯刚度的研究相对较少。李清海[11]、李生才[12]对钢丝网片增强的混凝土外墙板进行试验研究，结果表明，试件的比例极限强度、破坏强度及其对应挠度均随配筋率的增加呈线性增加趋势。童根树等[13-17]对自承式钢筋桁架混凝土板进行抗弯承载力试验研究，采用不同的计算方法确定其截面特性，并对结果进行对比分析，最终确定试件的截面惯性矩和抗弯模量。查晓雄等[18]对硅酸钙板-聚氨酯复合墙板的抗弯性能进行研究，通过理论分析以及试验研究的方式，提出用于硅酸钙板-聚氨酯复合墙板的理论简化公式并验证。但对于采用桁架龙骨并填充聚氨酯的复合墙板使用阶段抗弯刚度没有研究。在此背景下，参考现有相关研究成果基础上进行轻钢桁架龙骨外墙挂板使用阶段的理论分析，由此得到抗弯刚度影响因素并进抗弯承载力试验，从而为这种新型墙板的理论研究以及实际工程的设计和施工做出参考依据。

1 轻钢桁架龙骨外墙挂板刚度分析

轻钢桁架龙骨外墙挂板是一种新型轻钢结构墙板，构造如图1所示，主要由内外饰面层、聚氨酯保温层以及桁架筋龙骨三部分构成。其中桁架筋龙骨为墙板的主要受力构件，由于墙板中主要内容物为保温材料即硬质聚氨酯，聚氨酯材料的结构性能及受力效果不佳，因此龙骨布置采用纵横交错的方式。如图2所示，交错布置龙骨可以增大聚氨酯与龙骨的接触面积，减小每块保温层的面积，降低其荷载。其中龙骨的构造可参考图3。

图1 墙板构造示意图Fig.1 Schematic diagram of wall panel structure

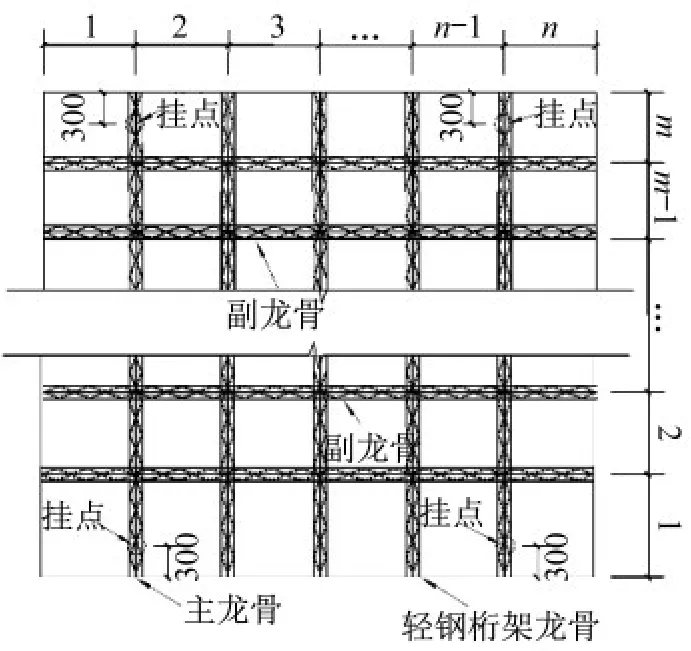
图2 龙骨交错布置示意图Fig.2 Sketch map of keel staggered arrangement

图3 龙骨构造示意图Fig.3 Schematic diagram of keel structure

轻钢桁架龙骨外墙挂板为一种新型的复合墙板，墙体中保温填充层占据主要体积但其弹性模量极低，对墙板的刚度贡献较低；内外饰面板的弹性模量相对较高，但饰面板体积较小提供的墙板抗弯刚度相对较低。因此为计算墙板的抗弯刚度性能，采用理论分析的方式同时分析桁架龙骨的刚度以及复合墙板整体的刚度，采用试验的方式验证。

1.1 龙骨刚度分析

桁架筋龙骨为墙板的主要受力构件，对桁架筋龙骨进行刚度分析确定龙骨为墙板提供的抗弯效果，只分析桁架龙骨的抗弯刚度，忽略聚氨酯保温层以及内外饰面板的刚度贡献，由此分析墙板弯曲刚度。

桁架龙骨截面如图4所示，上下弦钢筋为桁架主要受力构件，在桁架龙骨中腹杆钢筋为上下弦钢筋的连接构件，根据结构力学分析可将腹杆钢筋视为二力杆件[19]，因此腹杆钢筋对墙板刚度贡献可以忽略不计。

图4 桁架龙骨截面图Fig.4 Sectional view of truss keel

桁架龙骨的支座钢筋用来保证龙骨的形态防止龙骨自身的扭转，不对墙板整体提供抗弯刚度。综上所述龙骨刚度主要由上下弦钢筋提供，可得公式：

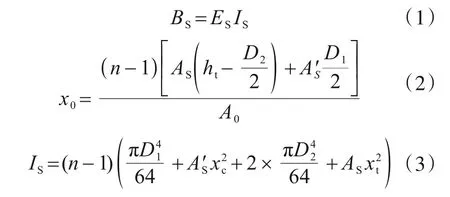
式中：BS为桁架龙骨的刚度；ES为钢筋的弹性模量，取 2.0×105N/mm2；IS为桁架惯性矩；D1、D2分别为上下弦钢筋直径；AS为受拉钢筋面积；A'S为受压钢筋总面积；A0为上下弦钢筋总面积；ht为钢筋桁架高度；xc为上弦钢筋型心与桁架中性轴的距离；xt为上弦钢筋型心与桁架中性轴的距离；x0为中性轴与桁架顶端的距离；n为纵向分段个数；（n-1）为纵向龙骨数。

1.2 复合墙板刚度分析

由于墙板为复合墙板由主要由三部分构成，分析墙板刚度时可依据复合墙板的刚度分析法来进行分析，即分析墙板断面处龙骨、聚氨酯与硅酸钙板的复合刚度，由此计算墙板弯曲刚度。

复合墙板刚度计算一般采用解析刚度法、刚度回归法、双直线法等推导并结合经验得出，本次理论分析采用等效刚度法推导轻钢桁架龙骨外墙板的刚度计算公式。假定饰面板面板和桁架筋龙骨均与聚氨酯芯材连接牢固，且可以达到变形协调，其弯曲应力沿每层截面高度的分布可视为一条连续的直线。如图5所示，墙板的弯曲刚度应分为四部分组成，桁架龙骨、内饰面板、外饰面板以及聚氨酯保温层。其中作为聚氨酯芯材的弹性模量较小，其作为抗弯构件给墙板提供的抗弯刚度远小于桁架筋龙骨和内外饰面板，因此计算墙板刚度时芯材部分可以忽略不计；上下弦钢筋为桁架主要受力构件，在桁架龙骨中腹杆钢筋为上下弦钢筋的连接构件，根据结构力学分析可将腹杆钢筋视为二力杆件[19]，因此腹杆钢筋对墙板刚度贡献可以忽略不计，桁架龙骨两端的支座钢筋用来保证龙骨的形态防止龙骨自身的扭转，不对墙板整体提供抗弯刚度。因此对墙板分析后对应的弯曲刚度应表达为

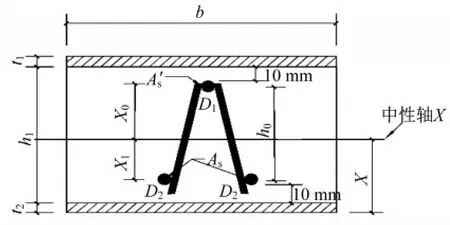
图5 复合墙板单个截面断面图Fig.5 Single cross-sectional view of composite wallboard

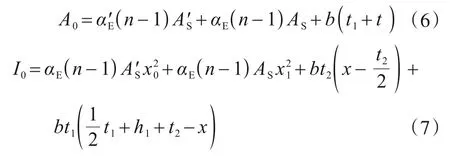
式中：Bf为复合墙板刚度理论值；x为中和轴距离内饰面板底端距离；A0为换算截面总面积；A'S为受压钢筋面积；AS为受拉钢筋面积；h0为钢筋桁架上下弦钢筋轴心距；α'E为受压钢筋与饰面板弹性模量之比；αE为受拉区钢筋与饰面板弹性模量值比；t1、t2分别为内外饰面板厚度；b为墙板纵向龙骨间距；I0为换算截面惯性矩；E为饰面板弹性模量；D1为受压区钢筋直径；D2为受拉区钢筋直径；n为纵向分段个数；（n-1）为纵向龙骨个数。

由上述墙板公式可知，墙板的刚度与纵向龙骨个数n-1、主龙骨的高度h0、龙骨上下弦钢筋直径（D1、D2）、饰面板厚度（t1、t2）相关。

2 试验研究

本次试验旨在通过主龙骨抗弯模型试验揭示墙板破坏的形式，确定影响墙板刚度的具体因素，验证墙板抗弯刚度理论公式。

2.1 试验构件

试验研究轻钢桁架龙骨外墙板的刚度，以长3 600 mm、宽2 400 mm的墙板作为试验构件，研究墙板主龙骨计算宽度部分的刚度从而反应墙板整体刚度。本次试验根据理论分析选取4个因素每因素3个水平，共设计了4组共12个试件，试件尺寸见表1，试件的构造见图6；墙板中钢筋桁架腹杆采用8 mm直径钢筋，钢筋的弹性模量E=2.0×105N/mm2；本次试验内外饰面板采用硅酸钙板，弹性模量取7.41×103N/mm2。

图6 龙骨交错布置图Fig.6 Staggered layout of keels

表1 试件尺寸表Table 1 Specimen size table

2.2 试验过程

为模拟墙板的均布受风状态，将试件水平放置，在预制的连接节点处将墙板与地面支座相连，形成挂板使用过程中四点支撑状态的受力状态，将其中上侧的连接节点固定在支座上，下侧支点限制水平竖直位移但可以转动。如图7（a）所示。实验采用位移计读数测量，测点沿龙骨布置，每根龙骨布置3个，另测量墙板中心挠度。

试件荷载采用配重块均匀铺装加载的方式，每个配重块20 kg，从墙板的中段均匀向两侧布置，通过位移计测量墙板中段的位移，如图7（b）所示。

2.3 试验分析

通过墙板试验可以得到四组不同因素试件的P-δ关系曲线。可计算出墙板试验的抗弯刚度，取墙板的计算长度3 300 mm，根据钢结构规范墙板主龙骨的极限挠度取计算取L/150，因此将挠度为L/150即22 mm时试验的荷载为墙板的刚度计算荷载，记为PL/150；在同种条件下采用式（3）计算桁架龙骨刚度、采用式（6）计算的复合墙板刚度，两者理论值与试验得到的刚度进行对比，验证理论值与试验得差异，分析差异原因。

2.3.1 纵向龙骨个数

A1、A2和A3试件纵向龙骨个数试验参数分别为3个、4个和6个，根据试验得到p-δ关系曲线，图8所示。由图像对比可知，三条曲线变化趋势基本一致，当位移超过11.45 mm后，随着龙骨个数少的试件承担荷载的能力逐渐降低，但曲线未有明显的破坏趋势，图形趋近直线试件刚度相对稳定；通过曲线可知A组试件墙板不同状况下的PL/150值，结合对应的两个理论刚度值得到表2。

由表2可知墙板的纵向龙骨个数从3个增加到到6个墙板的承载力极限荷载值提高19%，墙板试验刚度提高24.4%，纵向龙骨个数对墙板刚度影响较大。由于纵向龙骨个数影响的是桁架龙骨的布置，纵向龙骨个数越多龙骨布置密度越大，降低龙骨间聚氨酯块承担的荷载同时降低主龙骨上的均布荷载值，并且提高墙板的整体结构性能，因此对墙板刚度影响较大。

桁架龙骨理论刚度值随纵向龙骨个数变化增大，但与试验刚度值变化区间相近，且最大误差为12.0%，随着龙骨数增加误差逐渐缩小可见两者能够相互印证，证明采用桁架龙骨刚度表示墙板刚度具有准确性及一定的借鉴性。

复合墙板刚度值随计算间距变化而变化，变化趋势与试验刚度变化趋势相同。随着龙骨个数的增多墙板理论刚度增大，但其增大的幅度比龙骨计算得出的刚度增大幅度较小，这是由于计算中墙板大小不变内外饰面板的面积对墙板的刚度变化影响不变，但饰面板提供的这部分刚度随着龙骨个数的增多对墙板刚度影响逐渐减小，整体刚度依旧呈现提升趋势但趋势较缓，且刚度计算值在龙骨少的时候与试验值误差相对较大，最大值为115.2%。可见采用复合板抗弯刚度公式表达龙骨个数对墙板的刚度影响误差较大。

2.3.2 龙骨高度

B1、B2、B3和A1试件龙骨高度试验参数分别为120 mm、90 mm、80 mm以及100 mm，根据试验得到p-δ关系曲线如图9所示。由图像对比可知，四条曲线变化趋势相似但其刚度自始不同，随着龙骨高度的增大，试件承担荷载的能力逐渐提高。B1曲线末端有转折趋势，但极限荷载内图形趋近直线试件刚度相对稳定；通过曲线变化可知B组试件墙板不同状况下的PL/150值，结合对应的两个理论刚度值得到表3。

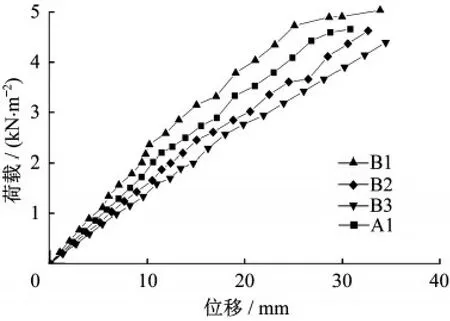
图9 桁架龙骨高度影响下墙板荷载-挠度曲线Fig.9 The load-deflection curve of the wall under the influence of the height of the truss keel

表3 刚度理论值与实际值比（龙骨高度因素）Table 3 Ratio of theoretical and actual stiffness stiffness（keel height factor）

由表3可知墙板的桁架龙骨高度从80 mm提高到120 mm墙板的承载力极限荷载值提高41.7%，墙板试验刚度提高38%，龙骨高度对墙板刚度影响较大。由于桁架龙骨高度影响的是桁架龙骨的结构，龙骨高度越大墙板越厚，通过提高龙骨的高度增大了各个截面到中和轴的距离，从而提高墙板的惯性矩，因此对墙板刚度影响较大。

桁架龙骨理论刚度值随龙骨高度参数变化，两者变化趋势相同但理论值变化速率较快，为且两者最大误差为13.5%，应是由于公式计算时忽略饰面板和保温层的抗弯作用，饰面板和保温层厚度不变时，随着龙骨高度的降低饰面板的面积矩降低，对墙体整体的刚度影响不在明显，从而使误差逐步降低。理论值与实验值两者虽能够相互印证，采用桁架龙骨刚度表示桁架高度对墙板刚度的影响准确性较好，具有一定的借鉴性。

复合墙板刚度值随龙骨高度参数变化，且变化趋势与试验刚度变化趋势相同，随着龙骨高度的增大理论刚度值增大，理论值与试验值误差逐步缩减，但理论刚度提高较大达到1.7倍，这是由于复合刚度计算公式中，计算了内外饰面层的刚度，随着各截面与中和轴距离的增大，提高了公式中的惯性矩，从而提高墙板的刚度，在考虑内外饰面板刚度的情况其误差增大。可见复合板抗弯公式不能精确地描述桁架龙骨高度对墙板刚度的影响。

2.3.3 钢筋直径

C1、C2、C3及A1试件钢筋直径试验参数分别为12 mm-10 mm-10mm、10 mm-10 mm-10 mm、10 mm-8 mm-8 mm、8 mm-8 mm-8 mm，根据试验得到p-δ关系曲线如图10所示。由图像对比可知，四条曲线变化趋势相近各个试件刚度自始不同，随着钢筋直径的增大试件承担荷载的能力逐渐提高，但观察可发现C1、C2曲线末端有刚度降低的现象墙板有破坏的趋势，图形趋近直线试件刚度相对稳定；通过曲线可知C组试件墙板不同状况下的PL/150值，结合对应的两个理论刚度值得到表4。

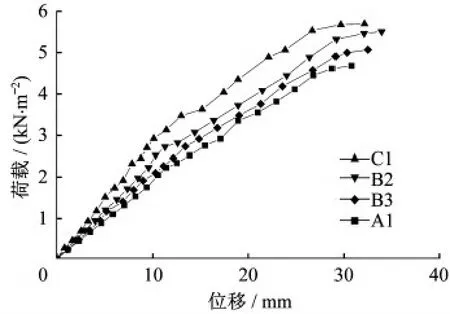
图10 钢筋直径因素影响下墙板荷载-挠度曲线Fig.10 The load-deflection curve of the lower wall panel affected by the diameter of the steel bar

表4 刚度理论值与实际值比（钢筋直径因素）Table 4 The ratio of rigidity theoretical value to actual value（rebar diameter factor）

由表4可知墙板的龙骨钢筋直径从8 mm-8 mm-8 mm提高到12 mm-10 mm-10 mm，墙板的承载力极限荷载值提高32.4%，墙板试验刚度提高25.7%，钢筋直径因素对墙板刚度影响很大。由于钢筋直径因素首先影响的是桁架龙骨上下弦钢筋的截面面积，钢筋截面面积越大钢筋的惯性矩越大为墙板提供的刚度更多。对比C1与C2、C3与A1的刚度提升均能达到10%，可发现采用上弦直径大于下弦的桁架龙骨设计方案更有利于墙板刚度的提升，这是由于钢筋布置会降低中性轴的位置，加大受压区截面积距离中和轴的距离提升抗压能力，从而提高跨中弯矩提高墙板刚度及强度，因此对墙板刚度影响较大。

桁架龙骨理论刚度值随钢筋直径参数而变化，两者变化趋势相同且变化速度相近，两者最大误差为12.8%，相对较小，误差值不随龙骨直径因素改变发生线性变化，在一定区间内进行波动，说明理论值与实验值的相关性较高。桁架钢筋直径的变化对墙板的抗弯刚度影响效果显著，此刚度理论值能反映上下弦不同时对墙板刚度的提升。墙板刚度实验值与理论值两者能够相互印证，且采用桁架龙骨刚度表示桁架钢筋直径对墙板刚度的影响准确性较高，此方法具有借鉴性，能够初步满足刚度计算的要求。

复合墙板刚度值随钢筋直径参数变化，且变化趋势与试验刚度趋势相同，随着龙骨钢筋直径的增大理论刚度值同时增大，虽然刚度计算值与理论值差距较大，但此组实验的刚度变化比较平稳，这是由于复合刚度计算公式中钢筋的弹性模量较大，在公式中钢筋提供的刚度比重远大于保温层及饰面层。且与试验值误差值相对稳定，可见复合板抗弯公式能够稳定表达钢筋直径变化对墙板刚度的影响，但差值依旧较大且不能精确表达。

2.3.4 墙饰面层厚度

D1、D2、D3和A1试件墙饰面层厚度参数分别为8 mm、10 mm、16 mm以及12 mm，根据试验得到p-δ关系曲线如图11所示。由图像对比可知，四条曲线变化趋势接近，其刚度也未见明显差异，随着墙饰面层厚度的增大只有D1曲线与其余曲线有明显分离，试件承担荷载的能力略有提高但并不明显，每条曲线接近直线没有明显转折趋势，极限荷载内图形趋近直线，试件刚度相对稳定；通过曲线变化可知，D组试件墙板不同状况下的PL/150值，结合对应的两个理论刚度值得到表5。

图11 墙饰面层厚度影响下墙板荷载-挠度曲线Fig.11 Wall panel load-deflection curve affected by the thickness of the wall finish

表5 刚度理论值与实际值比（饰面板厚度因素）Table 5 The ratio of theoretical and actual stiffness stiffness（decorative panel thickness factor）

由表5可知，墙板的内外饰面板厚度从8 mm提高到16 mm，墙板的承载力极限荷载值提高13.4%，墙板试验刚度值提高14.16%，内外饰面板厚度对墙板刚度影响较小。由于内外饰面板厚度主要影响的是中和轴的距离以及各截面到中和轴的距离，但相比之下，饰面板弹性模量约为钢筋弹性模量的1/270，改变内外饰面板厚度虽然提高中心轴位置但对墙板刚度的影响相对较小。

桁架龙骨理论刚度值不随内外饰面板厚度参数变化，但两者变化趋势相同且两者最大误差为12.0%，虽然公式计算时忽略饰面板和保温层的抗弯作用致使理论值低于实验值，但饰面板厚度变化对墙板实际的惯性矩影响较小，对刚度的影响不明显，因此理论值和实验值两者较为接近，可以采用桁架龙骨刚度表示内外饰面板厚度变化对墙板刚度的影响，且具有一定的准确性。

复合墙板刚度值随龙骨高度参数变化，且变化趋势与试验刚度变化趋势相同。随着内外饰面板厚度增大，理论刚度值增大，这是由于随着内外饰面板厚度的提高中和轴的位置提高，增大了内外饰面板到中性轴的距离，同时由于饰面板的面积大，对中性轴距离较远面积矩较大，对它的改变会较大地提高复合墙板刚度分析的惯性矩；但内外饰面板厚度的提高过程中理论刚度变化极大，且其试验值误差较大，可见复合板抗弯公式不适用与表达内外饰面板厚度对墙板刚度的影响。

3 结 论

本文采用理论分析与试验结合的方法，主要阐述了两种不同的刚度理论计算方法的优、劣势，并就不同因素对墙板的影响进行了讨论，结果如下：

（1）通过试验发现增加龙骨个数、龙骨高度、钢筋直径均可提高墙板刚度，最高幅度可达到38.00%；饰面板厚度增大对墙板的抗弯刚度提升较小，最高幅度只有14.16%。

（2）由试验可知，提高龙骨高度以及合理安排龙骨钢筋的直径更有利于提高墙板刚度，设计时宜选用钢筋直径为12 mm-10 mm-10 mm、10 mm-8 mm-8 mm的桁架龙骨并适当提高龙骨高度。

（3）采用复合墙板刚度公式计算时其刚度误差较大，结合试验可以发现，误差主要是由于饰面板提供的刚度理论值相对较大，但实际其提供的刚度相对较小这种理论假设与实际不相符造成的，可以对饰面板的刚度贡献进行有规律的折减尝试对墙板刚度进行分析，此种方法虽然不能精确描述墙板刚度值，但能描述墙板刚度的变化规律与实际墙板相符。

（4）采用桁架龙骨刚度代替墙板刚度。通过数据对比可以发现，大部分理论计算得到的刚度值小于试验的刚度值，主要是由于此种计算方式未考虑饰面层的刚度共同作用造成的，但从各个试验可知两者误差相对较小，最大误差为13.5%。采用这种理论值进行设计趋于保守，能够达到一般工程要求，但应注意在改变饰面板厚度的情况下此公式不随参数变化变化，此时不计算不能准确描述其刚度变化规律。