潮水流速对钻井隔水导管入孔影响的有限元分析

隋成龙，林家昱，李 进，尉文平，李留伟

（1.中海石油（中国）有限公司 天津分公司，天津 300459；2.中海石油能源发展股份有限公司 工程技术分公司，天津 300452；3.洲际海峡能源科技有限公司，北京 100088）

渤海是中国海上石油钻探开发作业的核心区域，据统计每年平均钻井数量在500口左右[1-3]。下隔水导管并建立钻井液闭路循环通道，成为渤海区域石油钻井作业的首要工序[4-6]。锤入法是目前渤海油田常用的隔水导管下入方式，相关技术已成熟应用。在渤海平台，对使用锤入法隔水导管的贯入特性、影响因素进行了深入分析[7]。此外，针对锤入法锤击次数及钻井隔水导管入泥深度也开展了综合性研究，确定了隔水导管的最小入泥深度[8-11]。随着海上探井及调整井的增多，大多探井及超大尺寸的隔水导管需要钻入法下入，且近年来随着隔水导管作为平台承载桩腿方式的提出，使用钻入法钻入后隔水导管需要进行固井作业，使隔水导管-水泥环-地层胶结强度更好，隔水导管承载力比锤入法更大。但是，采用钻入法下隔水导管存在钻入后老井眼重入问题，其不仅受海洋流速的影响，也受入孔尺寸大小的影响，但目前针对钻入法安装隔水导管研究较少[11]。

在钻完导管段后下入隔水导管时，若潮水流速较大，个别井会出现导管入海底孔眼困难的问题[12-13]。本文针对导管入孔时受潮流影响产生横向位置偏移问题，采用有限元分析软件建立流体-海水与固体-套管相耦合的有限元分析模型，进行了基于有限元方法的仿真模拟分析，计算在20 m水深、不同潮水流速下隔水导管下至海底孔眼位置井深时管尾横向位移大小，为指导钻入法隔水导管入孔提供理论依据。

1 潮水与隔水导管相互作用的流-固耦合有限元模型

1.1 几何模型及网格划分

渤海属于浅海，平均水深约20 m。渤海沿岸水浅，特别是河流注入地方仅几米深，而东部的老铁山水道最深，达到86 m[14]。为了使有限元分析模拟工况具有代表性，取模拟水深为20 m。海上钻井平台转盘面到海平面垂直高度按25 m考虑，隔水导管下入至海底时，管柱将产生最大偏移量。此时，隔水管入水长度为20 m，隔水管总长度为45 m。

隔水导管取外径508.0 mm、壁厚12.7 mm规格的套管。选取中心带有482.6 mm孔眼，长20 m、宽20 m、高20 m的正方体作为海水模块。隔水导管圆柱体中心线与该海水模块正方体中心线重合且底端位于正方体底面中心。以外径508.0 mm、高45 m的圆柱体的周向圆面表示隔水管外壁。假设潮水来流为X方向，绕流隔水导管后会形成左右对称的流场。为了简化计算，采用Y=0界面将海水和导管模型一分为二，取其同侧的1/2作为最终的导管和海水模块，隔水导管和海水几何模型见图1。

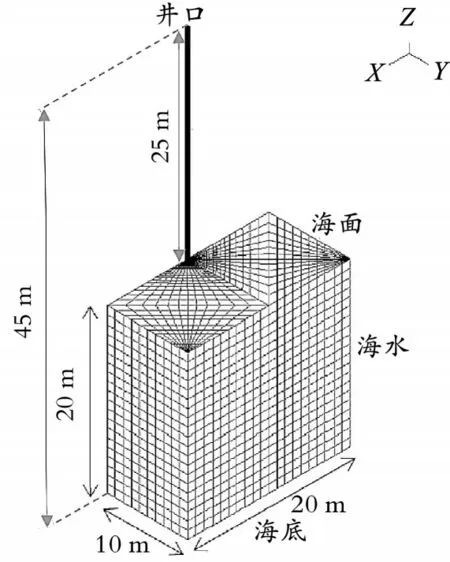
图1 隔水导管和海水几何模型Fig.1 Geometric model of conduit and seawater

1.2 材料模型及网格划分

导管选取各向同性弹性材料，弹性模量为2.07×1011Pa，泊松比为0.31，密度为7 850 kg/m3；海水选取层流流体，运动黏度为0.001 5 m2/s，海水密度为1 030 kg/m3，体积模量为1×1020Pa。在有限元分析模型中，对与海水接触的隔水导管半圆曲面，沿周向划分24层网格/180°，长度方向划分2层/m，采用节点数为4、厚度为12.7 mm的壳单元代表隔水导管体。网格划分后，隔水导管壳单元总数为2 160个。假定海底处隔水导管最大偏移量不超过0.50 m，则平均网格长度单位上最大横向偏移量为5.56×10−3m,单位网格长度的平均最大横向偏移应变（ξ）为1.11%，为小变形，满足网格精度要求。

海水采用8节点3D流体单元，根据高密度网格划分试算海水速度场梯度差异，在计算模拟结果趋于相同的前提下，减少网格和单元数量，优化网格布局，加大速度场梯度大的部位网格密度，减少速度场梯度小的部位网格密度，获得可接受的优化网格划分结果：对流体沿竖直方向划分网格1层/m，紧邻套管壁周向网格24层/180°，径向网格30层/10 m，其他三个竖直面网格1层/m。网格划分后，海水3D流体单元总数为19 200个，海水网格几何模型见图2。

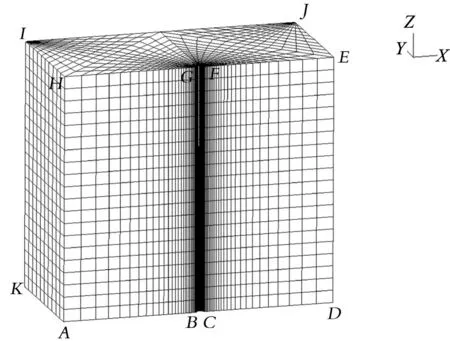
图2 海水网格几何模型Fig.2 Geometric model of seawater grid

1.3 边界约束条件

对隔水导管顶端，采用位移及旋转全约束；隔水导管竖直截面Y=0上各点Y位移约束。对海水模块，侧面A H I K施加法向流速VX，截面A B G H和C D EF施加Y向流速约束VY=0，截面I J K L施加Y向流速约束VY=0，半个套管曲面B C F G施加外法向流速约束V曲面法向=0，底面法向施加流速约束VZ=0。对导管施加与密度成正比的重力（9.8 N/kg)。海水与下部导管半圆曲面接触面设置为耦合接触面。

1.4 流速模拟设置及求解方法

在渤海区域大部分片区潮流流速不超过0.90 m/s。本文模拟计算潮水流速0.10～0.90 m/s时隔水导管受潮水绕流阻力产生的位移偏移量。由于难以获得稳态的速度场，本文采用瞬态计算，以1 s作为计算时间步长，计算获得加载后不同时间点管尾横向偏移量。导管偏移随着流场趋于稳定而最终达到平衡，此时偏移距离为最大偏移量。

2 潮水流速对隔水导管的影响

2.1 管尾横向偏移量

单个模拟工况下无法直接得到稳态解，因此首先求取不同加载时间对应的瞬态解，然后对比各加载时间瞬态解的变化趋势，推算或逼近稳态解。若加载时间长，则求出该时刻的瞬态解需要较大的计算量和计算时间。通过多次模拟计算结果对比可知，120 s后横向偏移量变化很小，横向偏移量已趋于恒定值。因此，出于计算时间和成本考虑，仅计算至120 s时管柱横向偏移量，以此作为稳态解的近似值。图3为管尾横向偏移量随时间的变化。

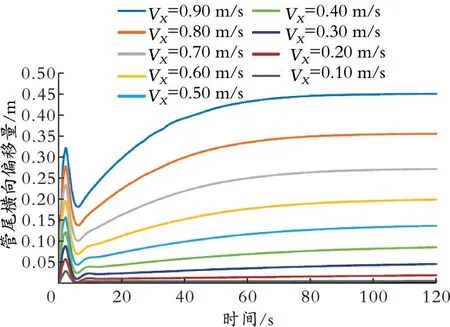
图3 管尾横向偏移量随时间的变化Fig.3 Variation of lateral offset of liner with time

从图3可以看出，模型加载0～120 s时，潮水流速越大，横向偏移量越早地趋于稳定；加载0～10 s时，管尾横向偏移出现明显波动，而后管尾横向偏移量不断上升，最终无限趋于恒定值。分析其原因，与初始加载边界流速形成海水冲击波并造成管尾持续向下游偏移且冲击波过后隔水导管管柱回弹有关。加载120 s时，各潮水流速下隔水导管虽并未完全稳定，但已接近各自的恒定值，即在120 s计算得到的管尾横向偏移量为最大偏移量的近似值。

2.2 流场分析

根据分析，流速越大，管尾横向偏移量越趋近于稳定，对应流场也越趋于隔水导管最终平衡时的稳定状态。对加载120 s潮水流速0.90 m/s时的海水模型流场进行分析。海水各空间位置及隔水导管周围海面各点速度失量图如图4所示。由图4（a）可以看出，在远离隔水导管的海水模型大部分空间内，潮水流速大小和方向不变，即近似处于未受扰动状态。由图4（b）可以看出，由于隔水导管的阻流作用，靠近隔水导管前端潮水产生很强的绕流，隔水导管后端附近区域产生局部涡流。

图4 潮水流速和隔水导管周围海面潮水流速矢量图Fig.4 Vector diagram of tidal velocity and sea tide velocity around riser conduit

为了对比分析潮水速度场变化情况，选取海水模型上端面(海面)作为研究对象，选取路径1−5共5条路径（见图5），取各路径最邻近单元节点，获得这些路径方向上各节点X方向的流速。

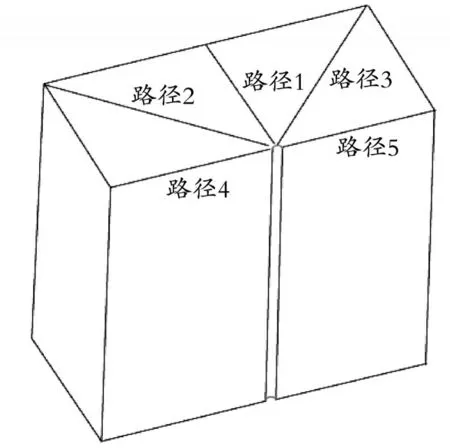
图5 评估潮水流速相对变化的不同路径位置Fig.5 Evaluate different path location for relative changes in tidal velocity

图6为路径1−5上各节点距导管中心水平距离与节点处（X方向）潮水流速关系曲线。由图6可以看出，路径4、路径2、路径1及路径3在距导管中心水平距离大于2 m时，X方向流速变化很小，表明受海水绕流影响小；路径5的流体随着远离导管中心，受流速影响逐渐减弱，在模型边界（距离导管中心10 m），流速仍未完全恢复至原值VX=0.90 m/s，表明海水流体模型路径5长度略显不足。

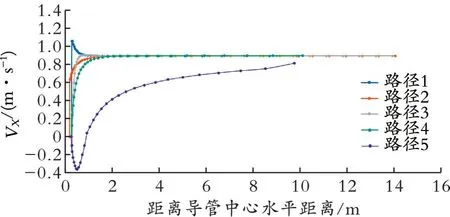
图6 路径1−5上各节点距离导管中心水平距离与节点处潮水流速关系曲线Fig.6 The relationship curve of horizontal distance between each node on route line 1 to line 5 and the riser and tidal velocity at the node

2.3 绕流阻力系数分析

以V2X/DX为纵坐标，VX为横坐标绘制曲线，结果如图7所示。由图7可知，当流速从0.10 m/s不断增加至0.90 m/s时，V2X/DX曲线不断趋于某一稳定值。

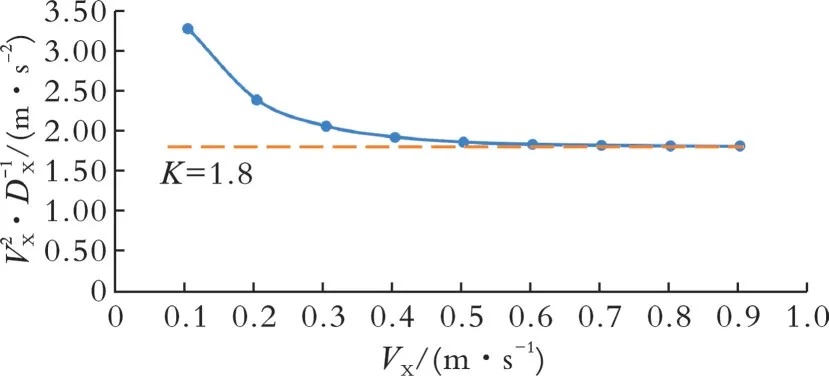
图7 流速与流速平方/管尾横向偏移量的关系曲线Fig.7 The relationship curve between velocity and velocity square/lateral offset of pipe shoe

由于导管管尾横向偏移量取自模型加载120 s时的计算值，其与稳态下的真实值有一定误差，而该误差随着模拟潮水流速增大而减小(见图3)。由此可知，导管偏移至稳定状态时，V2X/DX为一常数K，导管管尾横向偏移量与来流潮水流速的平方成正比，即：

根据曲线特征，K近似取1.8，即：

选取二维X-Z平面，将隔水导管简化为45 m线段，分别设置与三维导管模型相同的弹性模量、泊松比及密度，选取管单元，设置导管外径508.0 mm、壁厚12.7 mm，按2格/m进行网格划分。设置与密度成正比的重力（9.8 N/kg），并应用于整个模型；顶端施加全约束(位移和绕Y轴的旋转)，下端20 m施加横向（X方向）线载荷，模拟潮水对导管的绕流阻力。不断调整线载荷值，使管尾横向偏移距离分别等于图3中导管管尾横向偏移量，得到不同潮水流速下海水对导管单位长度的绕流阻力F，结果见表1。当量绕流阻力系数CD、雷诺数R e也列入表1中。

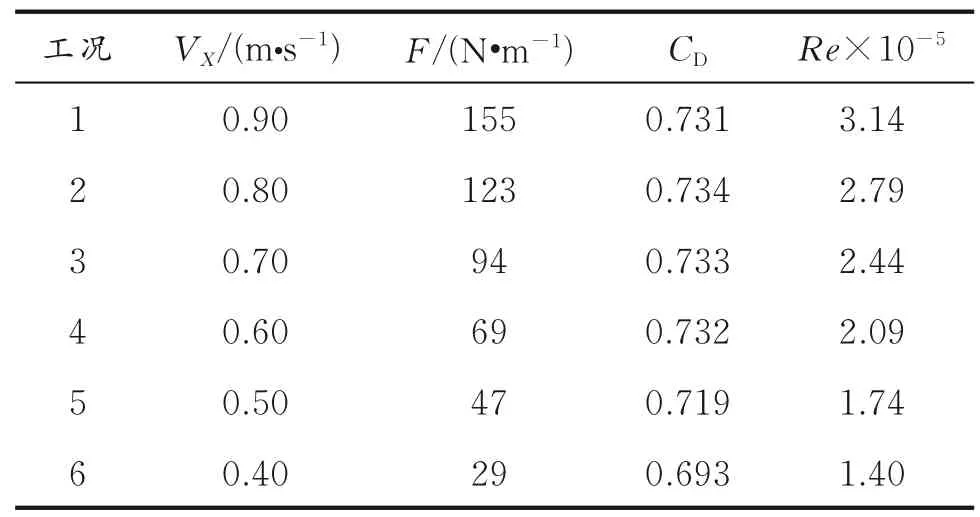
表1 不同潮水流速下导管受到的绕流阻力、当量绕流阻力系数及雷诺数Table 1 Flow resistance,drag coefficient and reynolds number of riser under different tidal velocity

根据垂直于圆柱体长度方向绕流的流体力学，单位长度管柱绕流阻力（当量线载荷）：

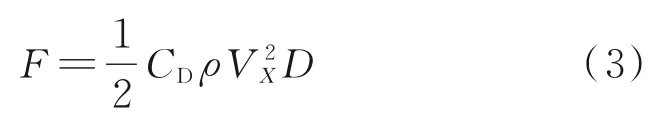
式中，ρ为海水密度，1 030 kg/m3；D为管直径，m。

将各参数及表1中当量线载荷值代入式（3），反推得到对应流速下海水对导管的当量绕流阻力系数。根据二维光滑圆柱体绕流理论可知，绕流阻力系数与雷诺数R e直接相关。根据R e=ρVX Dμ，得到对应数据(见表1)。

根据工程流体力学中无限长和有限长（L/D=5）圆柱体R e-CD数据曲线(见图8)判断，本算例雷诺数为1.40×105～3.14×105，合理的当量绕流阻力系数应介于两条曲线之间。将工况1−6的R e-CD数据点（图8中蓝色圆点）进行投影连线，结果显示，工况1−4导管的CD处于合理区间。这表明在来流潮水流速0.60～0.90 m/s情况下，隔水导管管尾横向偏移量计算值处于合理范围。

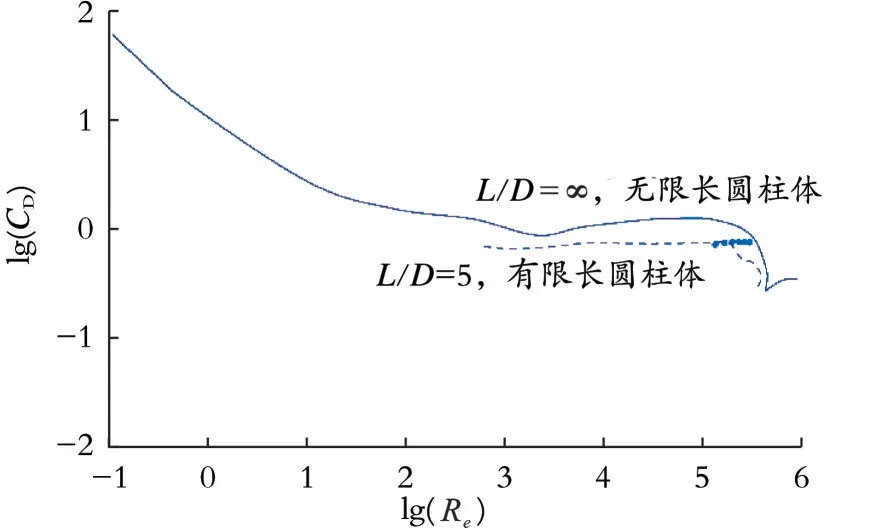
图8 有限长和无限长圆柱体绕流雷诺数与当量绕流阻力系数实验数据曲线Fig.8 Experimental data curves of reynolds number and drag coefficient of flow around finite and infinite cylinders

3 隔水导管下入分析及应用

3.1 隔水导管下入难度分析

在采用钻入法下入隔水导管的过程中，不仅受潮水流速和绕流系数的影响，还会受到井眼尺寸的影响。井眼尺寸大，隔水导管管尾允许的横向偏移量相应增大，因此需要结合不同潮水流速下隔水导管的横向偏移量，确定特定井眼尺寸在不同潮水流速下的导管入孔难度。图9为井眼与导管容许偏移量示意图。

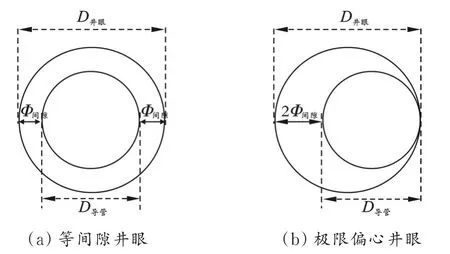
图9 井眼与导管容许偏移量示意图Fig.9 Schematic diagram of allowable deviation between wellbore and riser

由图9可知，隔水管管尾横向偏移量（DX）与井眼环空理论单边间隙（Φ间隙）存在如下关系：

（1）DX＜Φ间隙时，导管入孔不会遇阻；

（2）Φ间隙≤DX≤2Φ间隙时，导管入孔可能遇阻；

（3）DX＞2Φ间隙时，导管入孔易遇阻。

渤海区域海底平坦，多为泥沙和软泥质，钻进中钻井液冲刷井壁，井眼极易扩径[15]。常规508.0 mm导管段，常采用660.4 mm钻头钻进或孔眼。根据区域经验，隔水导管固井，按钻头直径计算的环空容积附加量不小于200%，由此可以推算出常规660.4 mm井眼实际井径在889.0 mm以上。

以扩径后井径889.0 mm计算，下入508.0 mm隔水导管，隔水导管横向偏移量DX＞2Φ间隙(381.0 mm)时，导管入孔易遇阻。对照隔水导管在不同潮水流速下横向偏移量的模拟结果知，若潮水流速大于0.83 m/s，则导管入孔易遇阻。

当190.5 mm≤DX≤381.0 mm时，若潮水流速为0.59～0.83 m/s，则导管入孔可能遇阻；若潮水流速小于0.59 m/s，则导管入孔不会遇阻。

在潮水流速大于0.83 m/s的工况下，为了防止隔水导管入孔困难，可在钻进起钻前反复大排量拉划，增大井眼扩径程度。最好的策略是，等潮水流速下降至0.59 m/s以下再下入隔水导管。

3.2 隔水导管下入应用

通过综合对比分析，选择平潮开孔、平潮下隔水导管是保证隔水导管下入风险最低的方案，但受天气、海况及作业进度影响，下隔水管作业节点往往随机性较强，无法严格按照平潮施工。

以渤海油田北部区域常见的三开井身结构探井L5井及S3井实际作业情况为例。在开孔条件相同的情况下，一开开孔钻具组合：26″PDC+X/O+9″DC×2+X/O+8″DC+8″（F/J+JAR）+X/O+5-1/2″HWDP×14。隔水导管下入情况见表2。由表2可知，L5井隔水导管下入过程中无遇阻显示，顺利完成一开作业；S3井处理遇阻用时3 h，处理至15∶00流速降低至0.75 m/s、流速方向北偏东34°，顺利实现入孔。结合两口井的实践情况对比，更好地佐证了有限元模拟结果的准确性。

表2 隔水导管下入情况Table 2 Entry condition of riser

4 结论与认识

（1）结合渤海区域导管作业环境，通过有限元分析软件ADINA，对潮水与隔水导管进行流固耦合有限元法计算分析，在0.10～0.90 m/s潮水流速下入孔时，导管管尾横向偏移量为0.3～44.9 cm。

（2）靠近隔水导管前端潮水产生很强的绕流，导管后端附近区域产生局部涡流。

（3）在0.10～0.90 m/s潮水流速工况下下，导管受到的单位长度绕流阻力系数与相关实验数据说明，该绕流阻力系数在正常的取值范围，也间接证实了本文计算得到的隔水导管管尾横向偏移量是可靠的。

（4）根据导管与入孔井眼的几何尺寸关系，建立了评估隔水导管入孔难易程度的判定条件。结合渤海实际情况得出，在潮水流速小于0.59 m/s时，不会发生遇阻现象；当潮水流速大于0.83 m/s时，可能会出现入孔困难现象。