蒸汽吐吞稠油热采产量递减分析方法研究

杨建平

（中国石油 辽河油田高升采油厂，辽宁 盘锦 124010）

产量递减分析作为油气井地层参数求取和单井控制储量计算的重要方法，在油气藏储量评价方面具有重要的作用[1-2]。目前，油田上采用最多的产量递减分析方法包括Blasingame[3]、NPI[4]和A-G法[5]。稠油黏度大，流体流动困难，因此稠油的开发一般通过向储层注高温蒸汽（蒸汽泡沫驱、氮气驱等）来降低原油黏度，以提高原油动用程度[6-8]。

国内外学者对稠油热采进行了大量的实验研究，认为稠油受温度的影响比较显著，稠油经过高温加热之后表现出牛顿流体特征，低温下表现为非牛顿幂率流体特征[9-10]。同时，国内外学者对稠油热采不稳定渗流理论进行了大量的研究。国外学者C.U.Ikoku等[11]首先研究了非牛顿幂率流体不稳定渗流数学模型并进行了井底压力动态分析。国内学者宋考平等[12]对稠油热采水平井和直井不稳定渗流数学模型进行了大量的研究，分析了不同参数对井底压力动态特征曲线的影响。但是，上述学者仅仅对稠油热采井底压力动态进行了分析，没有开展NPI和Blasingame现代产量递减分析方面的研究。

为了获得蒸汽吐吞加热半径和动态地质储量等参数，本文以不稳定渗流理论为基础，以蒸汽吐吞稠油热采为研究对象，建立牛顿-幂率流体径向复合油藏不稳定渗流数学模型，通过Laplace积分变换获得定产生产条件下井底压力解，通过定产与定压之间的关系，绘制稠油热采NPI和Blasingame现代产量递减特征曲线，分析各参数对产量递减特征曲线的影响。

1 物理模型

假定向一口直井注入高温蒸气，焖井一段时间之后开井生产。图1为稠油热采物理模型示意图。

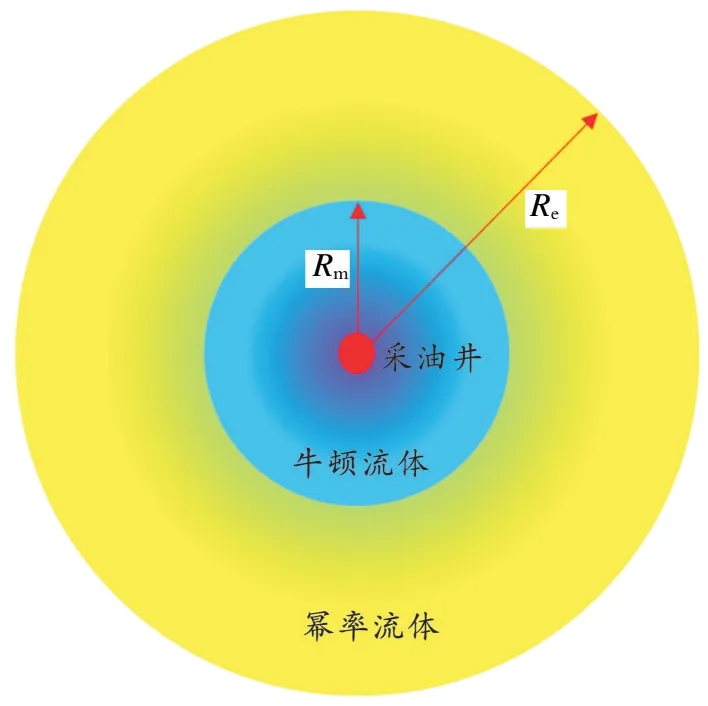
图1 稠油热采物理模型示意图Fig.1 Physical model of heavy oil thermal recovery

井位于油藏中心，注入高温气体之后，由于内区稠油黏度降低，可以采用牛顿流体描述。因此，采用牛顿-幂率流体径向复合模型来描述稠油热采物理模型。高温蒸汽所能波及的半径为Rm，外边界封闭，封闭外边界半径为Re。流体在储层中的流动满足等温渗流规律，采用Darcy定律来描述，根据文献[11]研究结果，幂率流体黏度与半径存在以下关系：

式中，μa2为外区幂律流体视黏度，mPa·s；μ*2为外区幂律流体的特征黏度，mPa·s；rD为储层任意位置到井筒无因次距离；RmD为无因次内区半径；n为幂律指数。

2 数学模型建立与求解

基于上述物理模型，建立Laplace空间牛顿-幂率流体无因次不稳定渗流数学模型及内外边界条件。

加热区牛顿流体渗流微分方程：

式（2）−（7）中所用到的无因次变量定义如下：

式中，k1为内区牛顿流体渗透率，D；k2为外区幂率流体渗透率，D；rw为井筒半径,m；Rm为牛顿流体区域半径，m；Re为封闭外边界半径，m；M12为牛顿流体区域与幂率流体区域流度比；η12为牛顿流体区域与幂率流体区域导压系数比；φ1、φ2分别为牛顿流体区域与幂率流体区域储层孔隙度；Ct1、Ct2分别为牛顿流体区域与幂率流体区域储层综合压缩系数，1/MPa；h为储层厚度，m；B为原油体积系数，即地下原油体积与地上原油体积之比，m3/m3；qsc为地面油产量，m3/d；s为Laplace变量。

式（2）和式（3）为v阶Bessel方程，方程通解为：

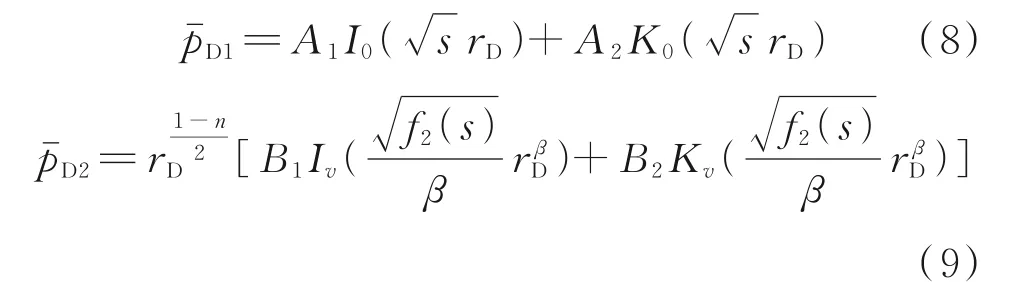
分别将式（8）和式（9）代入式（4）−（7）中，得到4个线性方程：

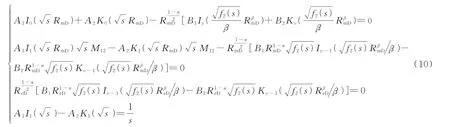
式（10）中有4个未知数A1、A2、B1、B2，通过高斯消元法得到系数A1、A2、B1、B2的值，将得到的系数返代入式（8），可以得到Laplace空间该模型无因次井底压力解。

3 NPI和Blasingame现代产量递减分析方法

3.1 NPI现代产量递减分析方法

如果基于井半径定义的无因次时间与基于井控面积定义的无因次时间存在以下基本关系：

基于上述时间代换，为了得到稠油热采A-G现代产量递减分析曲线，将线性方程式（10）中的代替，即可得到稠油热采NPI产量递减分析所用到的井底压力表达式：

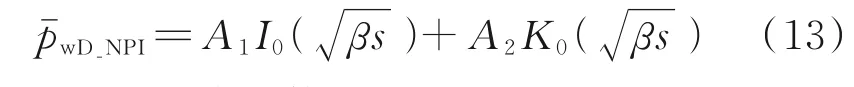
定义压力积分函数：

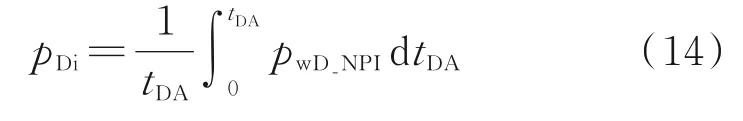
定义压力积分导数函数：

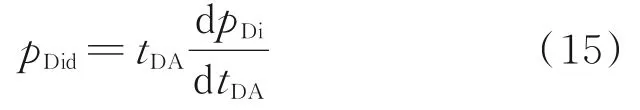
3.2 Blasingame现代产量递减分析方法

Blasingame现代产量递减分析曲线所用的时间为物质平衡时间，Blasingame现代产量递减分析方法所用的时间与无因次时间存在以下关系：

Blasingame现代产量递减分析规整化产量为：

Blasingame现代产量递减分析规整化产量积分及积分导数定义为：

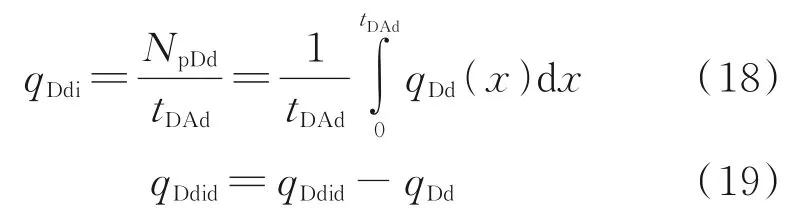
4 特征曲线及参数敏感性分析

对式（11）利用Stehfest数值反演得到实空间井底 压 力 解，再 根 据 式(17)−（19）得 到NPI和Blasingame现代产量递减分析特征曲线，结果见图2。

图2 稠油热采NPI、Blasingame现代产量递减特征曲线Fig.2 NPI and Blasingame production decline characteristic curve of heavy oil thermal recovery

由图2可知，根据NPI压力积分及压力积分导数曲线特征，该模型NPI和Blasingame现代产量递减曲线分为4段：第Ⅰ段为牛顿流体径向流阶段，该阶段NPI压力积分导数曲线呈值为0.5的水平线；第Ⅱ段为牛顿流体-幂率流体过渡阶段，该阶段NPI压力积分导数曲线呈上翘的直线；第Ⅲ段为幂率流体径向流阶段，该阶段NPI压力积分导数曲线呈斜率为(1−n)/(3−n)的直线；第Ⅳ段为拟稳态流动阶段，该阶段NPI压力积分导数曲线呈斜率为1.0的直线，Blasingame现代产量递减曲线呈斜率为−1.0的直线，β曲线呈值为1.0的水平线。从图2还可以看出，幂率指数n越大，表明流体流动阻力越小，压力波传播速度越快，所以幂率指数n越大，幂率流体径向流阶段NPI曲线越低，拟稳态流动阶段开始的时间越早。同时，幂率指数n越大，幂率流体径向流阶段Blasingame现代产量递减曲线越低（见图2（b））。当幂率指数n为1.0时，该模型简化为常规径向复合油藏模型，幂率流体径向流阶段NPI压力积分导数曲线呈值为0.5M2的水平线。

图3为牛顿流体与幂率流体流动区域流度比对NPI产量递减曲线和Blasingame现代产量递减曲线的影响。从图3可以看出，流度比越大，幂率流体径向流动阶段NPI产量递减曲线越高，主要是因为：流度比越大，说明储层稠油黏度越大，流体流动越困难。因此，牛顿流体与幂率流体区域流度比越大，NPI产量递减曲线幂率流体流动区压力积分曲线越高。流度比越大，幂率流体径向流动阶段Blasingame现代产量递减曲线越高。

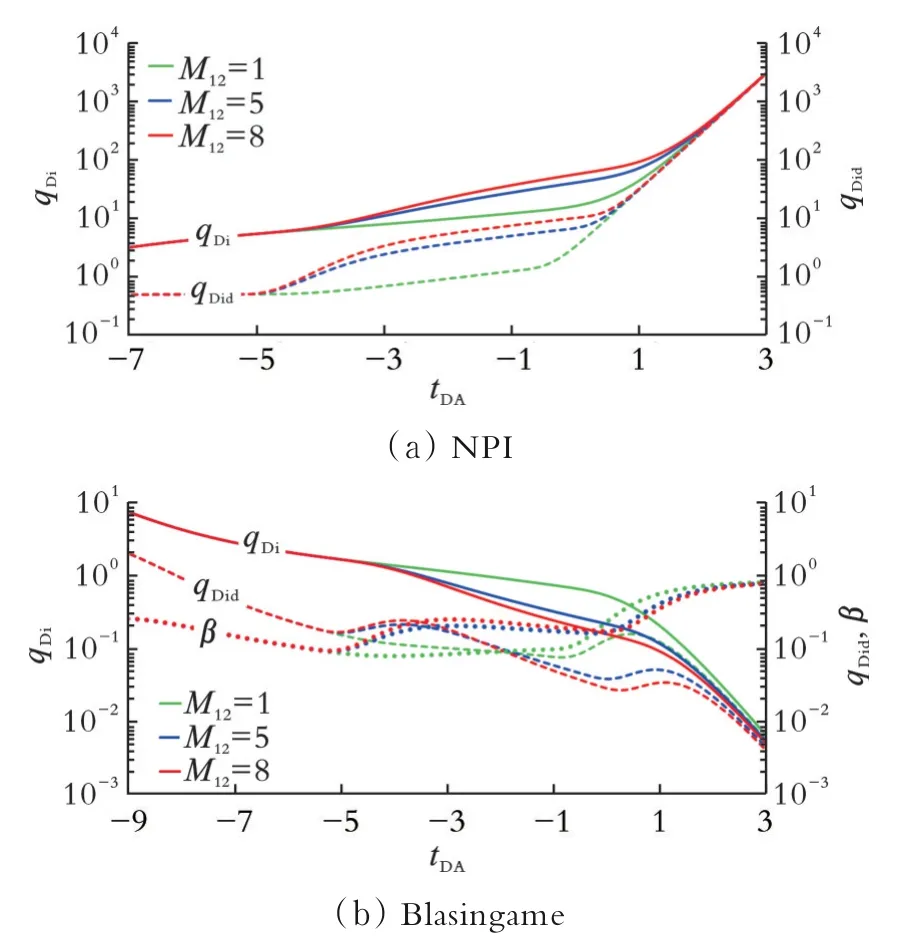
图3 流度比对NPI、Blasingame现代产量递减特征曲线的影响Fig.3 NPI and Blasingame production decline characteristic curves are influenced by mobility ratio

5 实例分析

辽河区块一口蒸汽吞吐采油井X，储层埋藏深度为−1 425～−1 603 m，射开储层厚度为10.4 m，储层孔隙度为32.2%，直井井筒半径为0.070 5 m，原油黏度为332.1 mPa·s，体积系数为0.91，原始压力为18.171 MPa。该井自投产以来，单井以定产量2.45 t/d生产，生产一段时间之后，该井产量开始出现递减。通过注水蒸汽焖井一段时间后，产量上升至3.42 t/d。

根据T.A.Blasingame[3]等的研究，在拟稳态流动阶段，压力重整流量曲线在拟稳态流动阶段双对数坐标中呈一定斜率的直线，且压力重整流量与流量重整压力存在以下关系：

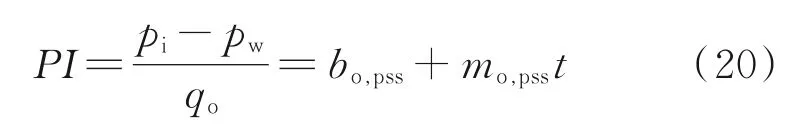
式中，(pi−pw)qo的倒数为式（12）有因次形式，通过无因次变量定义，不断地调节储层及外边界大小等参数，使理论曲线上下左右移动，最终得到拟合效果最好的曲线，在这种拟合曲线下得到的参数值就是解释结果。在同样的拟合参数下，将实测曲线与NPI理论曲线绘制在一张图中，通过微调各参数使最终NPI和Blasingame现代产量递减曲线都达到很好的拟合效果，即两种产量递减曲线起到了相互验证的作用，最终得到最准确的解释结果。曲线拟合之后得到了系数bo,pss和mo,pss的值，基于该值反算动态地址储量、储层渗透率和幂率指数等参数。系数bo,pss和mo,pss的具体表达式如下：

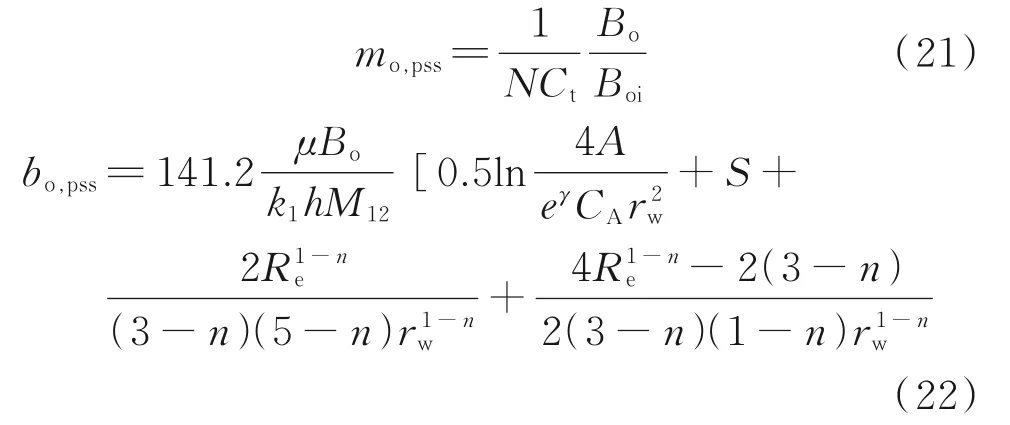
式中，Bo为原油体积系数；S为表皮系数；CA为油藏形状因子；Boi为原始地层压力原油体积系数；N为单井动态控制储量，t。

最终拟合得到的NPI和Blasingame现代产量递减曲线如图4所示。由图4可以看出，实测数据与拟合数据匹配效果很好。通过上述方法，求得X井动态储量为315.95×104t，幂率指数为0.2，流度比M12为8，加热半径为31.2 m，储层渗透率为32.1 D，单井控制半径为500 m。解释结果符合当地油田实际情况。

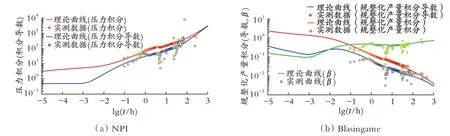
图4 X井NPI、Blasingame拟合曲线Fig.4 NPI and Blasingame fitting curve of well X

6 结 论

本文基于不稳定渗流理论，建立稠油热采不稳定渗流数学模型，分析NPI和Blasingame现代产量递减积分曲线，得到以下结论：

（1）稠油热采NPI和Blasingame现代产量递减过程可分为4个流动阶段：牛顿流体径向流阶段、过渡流阶段、幂率流体径向流阶段和拟稳态流动阶段。拟稳态流动阶段NPI积分导数曲线呈斜率为1的直线，Blasingame现代产量递减积分导数曲线呈斜率为−1.0的直线，曲线呈值为1.0的水平线。

（2）幂率流体径向流阶段NPI积分导数曲线呈斜率为(1−n)/(3−n)的直线，且幂率指数越大，幂率流体径向流阶段NPI积分及积分导数曲线越高；流度比越大，NPI积分导数曲线斜率小于0.5，幂率流体径向流动阶段Blasingame现代产量递减曲线越高。

（3）通过实例检验可知，本文模型和方法可以很好地对稠油热采井进行单井控制储量计算。