促进数学核心素养发展的专题变式教学的建构——以专题课“隐圆”为例

李 娃

（金华市永康中学 浙江 金华 321300）

“专题教学”一般指的是以某一类知识或思想、方法等为内容载体，以梳理数学知识、探索解题策略、掌握思想方法等为目标，而开展的一系列教学。其特点是,数学问题的系列性、数学知识的综合性、思想方法的收敛性。“变式教学”是基于数学知识和数学问题的相似性、联系性与结构性，从已经提出和解决的数学问题出发，通过改变问题的情境、条件、障碍或目标，提出蕴含着新的数学概念、原理、方法或结论的新问题的教学。 《义务教育数学课程标准2022版》指出，初中阶段数学核心素养主要表现为：抽象能力、运算能力、几何直观、空间观念、推理能力、数据观念、模型观念、应用意识、创新意识。 中考前的最后复习阶段是进一步促进数学核心素养发展的关键时期，而专题复习课中恰当的变式教学的建构为核心素养的发展搭建了很好的平台，下面就以专题课“隐圆”为例，谈谈变式教学如何建构。

1.明确变式教学的目标

1.1 分析题目已知和未知条件，经历如何想到构造圆、如何构造圆的过程，从圆的定义着手实现隐圆的构造。

1.2 在隐圆构造的过程中，如旋转构圆、滑动构圆、折叠构圆、对称构圆……它们的本质都是定点定长，体会变中不变的化归思想。

1.3 通过以上的过程，体会到从确定圆的方法着手，变幻出破解圆的隐身术的不同方法。

1.4 体会到模型的获得首先需要对模型本身的特点、功能等掌握的基础上，才能构造出相应的模型，体会模型思想在解决问题中的重要性。

1.5 促进学生的抽象能力、模型观念、创新意识等核心素养的发展

2.选定变式教学的载体

2.1 解决问题与提出问题相结合。如在教师提出变式并解决之后，可以放手让学生自行编拟变式题。

2.2 运用数学知识与建构数学模型相结合。如可以一边利用圆的定义和性质解决问题，一边建构出三种隐圆模型：定点定长型、定边对定角型、四点共圆型。

2.3 掌握数学知识技能与发展数学关键能力相结合。如通过不断的变式使学生掌握隐圆的三种模型，进而发展学生的数学抽象能力、数学建模能力、化归能力。

3.确定变式教学的策略

3.1 变任务驱动为思维导向

如给出引题之后，让学生自主思考，看谁的方法最多、最快。这样学生就不会仅满足于求出∠BDC的度数这个任务驱动，而会更深入地思考，找到一种既简便又全面的方法，做出隐圆，从而把学生的思维导向这节课的主题——隐圆。

3.2 强化变式教学的整体设计

（1）引题——引出模型

例 1.如图 1，在 ΔABC中，AB=AC，∠A=60°，点D在ΔABC的外部，且在BC的上方，如果AD=AB，那么∠BDC=____°.

图1

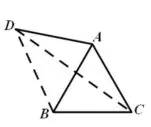
图2

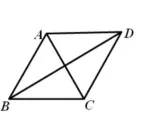
图3

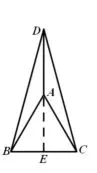
图4

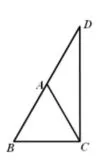
图5

图6

设置此例为引题的目的是因为此题方法众多，但有的方法很繁琐，如生1的方法，而且还得对D点的位置进行分类，生2～生4的方法虽然简便，但取的都是特殊位置，不全面，唯有生5的方法，既简便、全面，又逻辑严密。学生从比较这几种方法中，充分体会到作出隐圆后，可以利用圆的相关知识，如圆心角、圆周角，弦，弧等的关系来使解题过程优化简便，从而深刻认识到学习隐圆的必要性。

变式.如图7，在四边形ABCD中，DC∥AB，BC=1，AB=AC=AD=2，则BD的长为____.

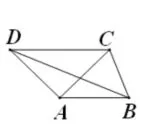
图7

在变式之后由学生及时提炼出第一种隐圆的模型：定点定长型。

（2）源题

例2.如图8，正方形ABCD的边长为2，将长为2的线段EF的两端放在正方形的相邻的两边上同时滑动，如果点E从点A出发，按A→B滑动到B止，同时点F从点B出发，按B→C滑动到C止，则线段EF的中点M经过的路径长是____.

图8

（3）渐变

可以通过改变载体如把正方形变成矩形、菱形等，也可以改变点的位置，或者加入动点，还可以改变运动的方式，如变旋转为滑动、折叠、对称等，或者改变问题的结论等，但不管怎么变，都是要形成定点、定长。在原题的基础上，继续变式：

变式1.如图9，在矩形ABCD中，AB=2，AD=3，点E、F分别是AB、BC边上的两动点，且EF=2，点M为EF的中点.连结DM，则DM的最小值是____.

图9

图10

变式2.在变式1的基础上，取点N为AD边上一动点，连结CN、MN，则CN+MN的最小值是____.

变式3.如图11，在矩形ABCD中，AB=，AD=3，点P是AD边上的一个动点，连结BP，将ΔABP沿BP折叠，A落在A'.

图11

（1）连结A'D，则A'D的最小值是____.

（2）连结A'C，设A'C的中点为Q，当点P从点A出发，沿边AD运动到点D时停止运动，则点Q运动的路径长是____.

（4）递变

除了定点定长型还有什么情况下可以构圆？变式4～变式6设置的目的就是让构圆模型的方法进一步延伸，提炼出定边对定角型、四点共圆型。

变式4.如图12，正方形ABCD中，AB=4，动点E从点A出发向点D运动,同时动点F从点D出发向点C运动，点E，F运动的速度相同，当它们到达各自终点时停止运动，运动过程中线段AF，BE相交于点P，则点P运动的路径长是____.

图12

变式5.如图13,等边三角形ABC的边长为4，E、F分别是AC、BC边上的两个动点，且CE=BF，连结AF、BE，交点为P，则CP的最小值是____.

图13

变式6.如图14,等边三角形ABC的边长为4，P为AB边上一动点，PD⊥BC，PE⊥AC，垂足分别为D、E，则DE的最小值为____.

图14

（5）总结

由学生总结如何构圆，哪些情况可以构圆？圆可以解决哪些问题？怎么解决？

3.3 在变式中促进学生核心素养的发展

有了整体的教学设计后，教学中恰当的课堂提问能起到穿针引线的作用，有助于学生形成良好的知识和认知结构。在引题部分，教师可以追问生5为什么想到画圆？由学生概括出这3条线段的特征：共端点等线段，然后联系圆的定义抽象概括出第一种隐圆模型：定点定长型，培养学生的抽象概括能力。

教师继续追问：哪些运动会出现这种情况？生：旋转、滑动、折叠、对称……

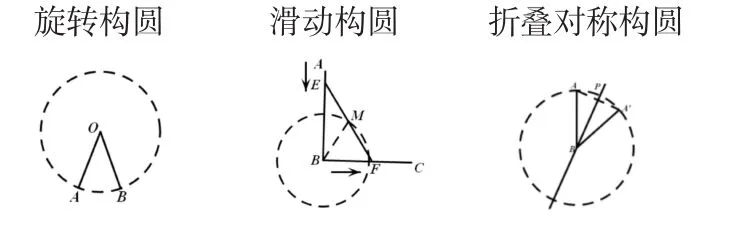
师：为什么这几种运动可以构圆？

生：因为它们的本质都是定点定长。通过这些运动的变式，目的是让学生体会变中不变的思想，进而培养学生的化归能力。

变式4～变式6之后继续让学生抽象概括出隐圆的另两种模型：定边对定角型和四点共圆型，培养学生的模型观念。

3.4 增强学生在变式教学中的自主性

教师在变式时，要揭示变式产生的思维过程，然后可以放手让学生自己提出变式，这样做的目的是加强学生对这类问题的理解，逐渐把知识、方法内化，培养学生的创新意识。如在源题之后、渐变题之后让学生接着变式。

生1：线段EF的中点M经过的路径与正方形边长围成的面积是____.

生2：EF的两个端点始终落在正方形的边上，按逆时针方向滑动一周，线段EF的中点M经过的路径长是____.线段EF的中点M经过的路径与正方形边长围成的面积是____.

生3：如图15，在矩形ABCD中，已知AB=2，AD=3，长为2的木棒EF紧贴着矩形的边逆时针方向滑动一周，木棒的中点M经过的路径长是____.中点M在运动过程中所围成的图形的面积是____.

图15

生4：如图16，矩形ABCD中，AB=2，AD=3，点F、N分别是AB、BC边上的两动点，点E在AD边上且AE=2，将ΔAEF沿EF折叠形成ΔMEF，连结MN，DN，则DN+MN的最小值是____.

图16

生5：如图17，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将ΔAMN沿MN所在直线折叠得到ΔA'MN，连结A'C，则A'C长度的最小值是____.

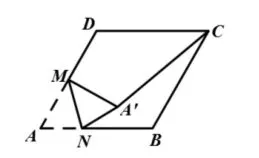
图17

本课中，利用变式教学把隐圆的问题串成串，教师帮助学生在复杂的问题中学会抽丝剥茧，运用数学思想，多题化归，抽象概括出此类问题的三种基本模型，最终达到促进数学核心素养发展的目的。