用锐角三角函数证题

孙利华

有些几何问题的证明，看似繁难，但若能够巧妙地运用三角函数，将能化繁为简，使问题得以巧妙地解决.

1 证线段相等

例1 图1

如图1，△ABC中，AB=AC，P是BC上任意一点，PD⊥AB，垂足为D，PE⊥AC，垂足为E，BF⊥AC，垂足为F.

求证：PD+PE=BF.

证明 设∠C=α，则

∠ABC=α.

因为PD=PBsinα，

PE=PCsinα，

BF=BCsinα，

所以PD+PE=PBsinα+PCsinα

=（PB+PC）sinα

=BCsinα=BF.

2 证角相等

例2 图2

如图2，在△ABC中，∠A=90°，AB=AC，AE=13AC，BD=13AB.

求证：∠ADE=∠EBC.

证明 作AM⊥BC，垂足为M，EF⊥BC，垂足为F.

不妨设AB=AC=3a，则易求得

DE=5a，BE=10a，BF=22a，

根据三角函数定义，得

cos∠ADE=ADDE=2a5a=25，

cos∠EBC=BFBE=22a10a=25，

所以cos∠ADE=cos∠EBC，

所以∠ADE=∠EBC.

3 证不等式

例3 图3

如图3，若CD为△ABC斜边AB上的高，求证：AB+CD>AC+BC.

证明 令AB=c，

∠A=α<90°.

因为AC=ccosα，BC=csinα，

CD=ACsinα=csinαcosα.

所以 （AB+CD）-（AC+BC）

=c（1-sinα）（1-cosα），

又因为α是锐角，

所以1-sinα>0，1-cosα>0，

则（1-sinα）（1-cosα）>0，

从而可知（AB+CD）-（AC+BC）>0，

即AB+CD>AC+BC.

4.证定值问题

例4 图4

如图4，过正方形ABCD的顶点A的直线交BC于点P，交DC的延长线于点Q，求证：1AP2+1AQ2为定值.

证明 设正方形的边长为a，

∠BAP=∠AQD=α，

在△ABP中，∠B=90°，a=AP·cosα，

a2=AP2·cos2α，

所以1AP2=cos2αa2.

同理有1AQ2=sin2αa2，

所以1AP2+1AQ2

=cos2αa2+sin2αa2

=cos2α+sin2αa2=1a2.

因为a为定值，

所以1AP2+1AQ2为定值.

5.證比例式

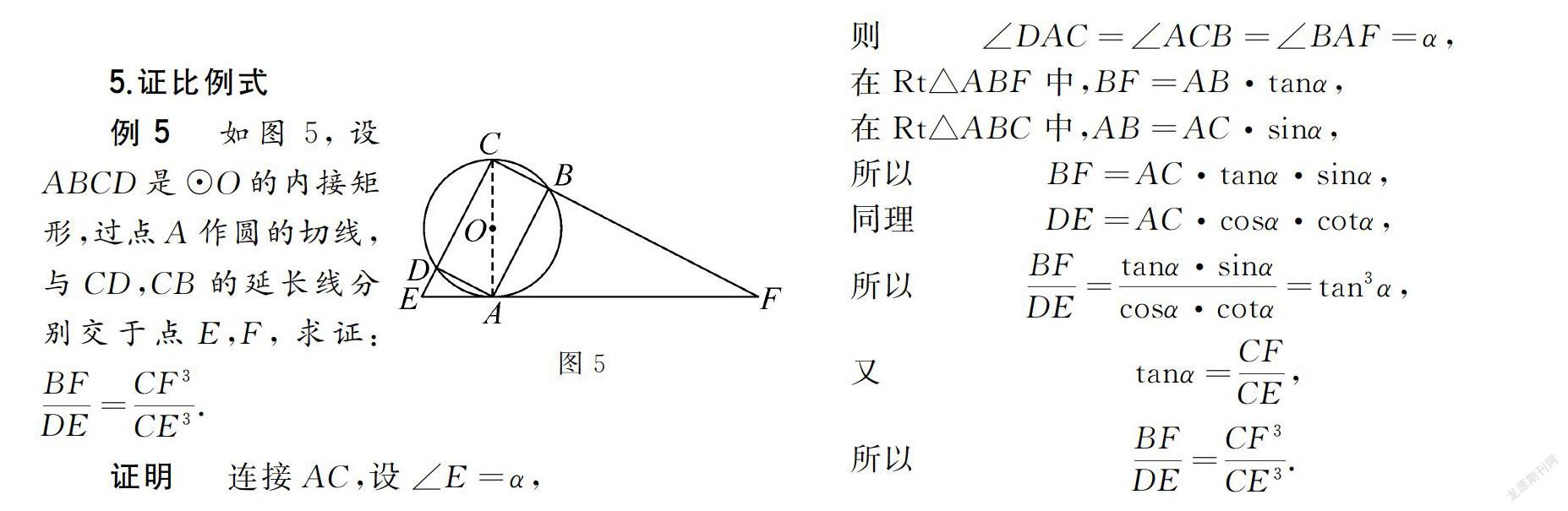
例5 图5

如图5，设ABCD是⊙O的内接矩形，过点A作圆的切线，与CD，CB的延长线分别交于点E，F，

求证：BFDE=CF3CE3.

证明 连接AC，设∠E=α，

则∠DAC=∠ACB=∠BAF=α，

在Rt△ABF中，BF=AB·tanα，

在Rt△ABC中，AB=AC·sinα，

所以BF=AC·tanα·sinα，

同理DE=AC·cosα·cotα，

所以BFDE=tanα·sinαcosα·cotα=tan3α，

又tanα=CFCE，

所以BFDE=CF3CE3.