阅读素养：解密数学非连续性文本的隐性提升

江苏连云港市东海县和平路小学（222300）徐 贺 张 媛

数学中的图表、公式、符号等都是非连续性文本，非连续性的文本特点要求学生会阅读文本，能从图文等素材中找出有价值的信息。生活中，大量的碎片信息如浪潮般涌来，非连续性文本阅读不仅能促使学生的数学审题能力提升，还能促使学生适应社会发展。因此，教师必须重视非连续性文本的阅读教学，培养学生的阅读素养。

一、理解非连续性文本与数学阅读素养的内涵

1.了解：概念解读

所谓非连续性文本，是相对连续性文本而言的。连续性文本是句子或段落组成的文本材料，而非连续性文本是以图文、数据、票据等形式呈现的文本材料，具有直观醒目、概括性强、易于比较等特点。

核心素养包括必备素养和关键能力，笔者认为阅读素养是必备素养的一部分。如果说公式、定义等知识是学习数学的“外在”，那么数学思想、数学价值、数学情感等就是数学学习的“内涵”。

2.探寻：数学价值

重视数学非连续性文本的阅读是提高数学审题能力的新方向。在数学学科中，非连续性文本贯穿各年级、各单元，如“数与代数”“概率与统计”“综合与应用”等。学生阅读非连续性文本的能力体现了学生的数学素养。数学非连续性文本的阅读着重点与语文不同，数学不仅关注阅读审题能力的提升，还要求学生学会把信息转化成数学思考，从而提高综合运用能力。

3.厘清：相互关系

重视数学非连续性文本的阅读是为了提升学生的解题能力。而数学阅读素养是在非连续性文本的阅读过程中慢慢形成的，它引领着数学思维，是影响数学方法的隐性存在。非连续性文本阅读水平与数学阅读素养是相互影响的（如图1）。

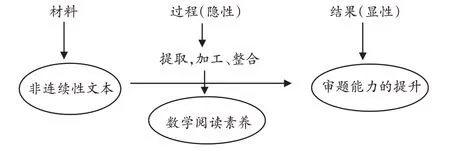
图1

二、利用数学非连续性文本资源，回归阅读素养的教学求解

教师重视非连续性文本资源的利用，不仅是为了提高学生的解题能力，还是为学生数学阅读素养的提升做铺垫。如果说学生掌握的知识是数学素养的“表”，那么学习过程中的数学思想、数学价值等就是数学素养的“里”，是蕴藏在知识和能力背后的隐性提升。

1.图文交织，筛选信息资源，培养专注力

詹姆斯·瓦特还是孩童时，就一边观察上下跳动的壶盖，一边思考：为什么水汽能够使沉重的壶盖跳动？后来他发明了蒸汽式发动机。这告诉我们：成绩的取得离不开认真的观察、严谨的思考、理性的坚持。非连续性文本通常措辞简练、信息量大，以碎片化的形式呈现。利用这种信息资源，可以培养学生在零碎的信息中保持细心、专心的专注力。如针对三年级学生的一道训练题（如图2）。

图2

本题数据杂、信息量大，但其实只要“去其糟粕，取其精华”，就会发现此类非连续性文本资料并没有那么复杂。学生只要厘清头绪，筛选有用信息，就能找到思维起点。由此看出，阅读非连续性文本的核心就是寻找关键信息。

（1）捡豆式筛选信息，指向直观阅读

不论是连续性文本还是非连续性文本，大部分学生阅读时首先都会简单了解文意，明确文本中提供的基本信息，寻找基本信息中的关键词，即零散式信息。根据学生的年龄特点，教师在教学中可以有针对性地指导，使学生静下心来读通文本，圈画关键词，不漏字、添字等。

笔者教学时常发现，一些学生不重视审题，经常一扫而过，有时还没读完就感觉此类题目很熟悉，认为自己已经知道题目大意，急于下笔。事实上，题目考查的内容已经改变，陷阱已经设好。因此，教师不仅要指导学生学会从众多信息中筛选相关内容，还要学会加工提取，更要有耐心。图2中的非连续性文本主要由两部分组成：家庭成员和营养片说明书。解决问题的关键是要从说明书中“捡出”相关信息，这有可能涉及产品规格、建议用量以及产品成分。

（2）剥茧式筛选信息，指向知识连接

阅读文本时，根据题意把有联系的信息抽丝剥茧，用箭头或者图形将筛选好的信息罗列出来，由此分析这道题想考查什么样知识点，逐步找出条件和问题间的数量关系，一层一层、一步一步地解决问题。筛选信息时应避免将注意力集中在一些无关的信息上。

寻找解决问题的相关信息，即有用信息，排除干扰信息，根据信息链找出关键信息，是解决问题的关键。因此，教师要指导学生审题时注意数量间的关系，留心关键词、关键句，不能忽视细节和词语的含义，也不能凭经验揣测题意。许多学生做错题就是因为在分析信息时过于急躁，不关注关键信息间的联系，或者因思维定式导致出错或思维受阻。对于本题，应筛选出所需的信息，包括产品规格、建议用量，排除产品成分。

（3）切入式筛选信息，指向综合能力

直奔重点，根据问题判定用什么样的方法来解决这道题。以问题为脉络直切关键信息，最能体现学生的综合素养。要让学生从多方面、多角度、多途径进行思考：以什么方式来处理问题与条件的关系？画图、列举还是画思维导图？一种方式不行，就几种方式一起试一试。此外，还要避免思维定式的影响，注重数形结合，有时甚至要将之前的思路全部推翻，重新寻找解题方向。层层筛选信息，这样，遇到再复杂的问题我们也能找到解决方法。针对本题综合信息：想到“建议用量”→找到“建议用量”→分析整理重要信息“就读于星星幼儿园大班的明明和爸爸妈妈”→判断人数为3人→总的每日建议用量为5片→根据数量关系解决问题。

2.数字解码，分析信息资源，培养求真精神

学生学习过程中习惯了被动接受、点头认同、保留意见，这样看似学习了新知、提升了能力，却丢失了难能可贵的品质——求真。斯托利亚尔指出：“数学教学也就是数学语言的教学。”数学语言包含文字语言、符号语言、图形语言，数学文字语言通俗易懂，数学符号语言概括性强，数学图形语言直观明了。根据数学语言的特点灵活转化表达，是学生准确阅读文本、提升审题能力的有效方法。

（1）分析数学知识：知其然

阅读数学非连续性文本有利于培养学生的审题能力，为适应当下和未来生活储备必要的知识和技能，同时促进学生数学阅读素养的提升。非连续性文本题目的审题是一种解码性的审题，目的是分析材料，筛选并整合文本中的重要信息。教师教学时要对非连续性文本进行比较分析，找出材料与材料之间的区别，并分析信息之间的逻辑关系，进行分析、比较、梳理，进而学会概括。

例如教学“3的倍数”，学生做图3中的题时，在圈画中观察到3的倍数的特征和2、5的倍数的不同，明白不能只观察个位上的数，还要分析各位上数的和，把图与各位上数的和进行整合，通过数字解码将非连续性文本转化成数学思考，经历分析、比较，抽象出数学模型，在建立模型的基础上确定解决问题的方法，这一系列过程需要一定的数学基础和直觉。

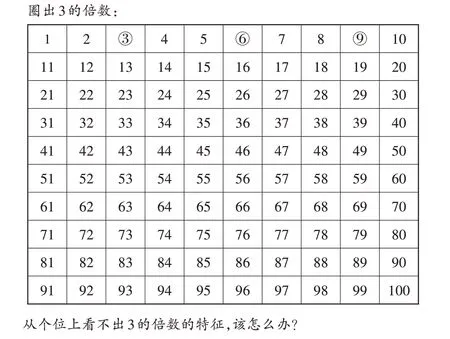
图3

（2）分析数学本质：知其所以然

很多学生学完“3的倍数”后，了解了3的倍数的特点，即将各位上的数相加，如果和是3的倍数，那么这个数就是3的倍数，会产生疑问：为什么2和5的倍数只看个位上的数就可以了呢？把这个问题彻底弄明白，学生就能“知其然”且“知其所以然”了。例如117这个数，百位上的1表示1个百，除以2后没有剩余，十位上的1表示1个十，除以2后也没有剩余，个位上的7表示7个一，除以2后有余数，所以117不是2的倍数。同样的，100÷5没有剩余，10÷5也没有剩余，7÷5有余数，所以117也不是5的倍数。而100÷3余1，10÷3也余1，合起来余2，加上个位上的7就是9，9÷3没有剩余，所以3的倍数要看各位上数的和是否是3的倍数。而因为除个位外，其他数位上的数都能被2、5整除，所以2、5的倍数只要看个位上的数。这样一解释，学生便醍醐灌顶，在较真、寻真、悟真中识得数学知识的本来面貌，提升数学学习水平。

3.联系身边信息资源，培养创新精神

创新不是胡编乱造，它可以在生活中感悟。数学与生活实际紧密相连，应用生活题材深化数学教学，对生活中的非连续性文本资源进行整合探究，能让学生感受数学知识对生活的重要性。

（1）生活中的“数学化”

生活中的非连续性文本资源随处可见，如广告、车票、购物清单等，教师可充分利用这些资源创新问题，灵活教学。这样不仅可以丰富数学课堂教学内容，还可以激发学生的学习兴趣，锻炼学生运用知识解决实际问题的能力。

比如，在一次测试中，笔者以火车票（如图4）为素材，结合出发地、目的地、乘车时间、车次以及车厢编号等信息对学生进行考查，不仅考查了学生提取和整合信息的能力，还让学生深刻地感受到生活中随处可见数学，体会学好数学的必要性。

图4

（2）数学中的“生活味”

数学是一门比较抽象的学科，适当的引导可以让学生发现数学与生活的紧密联系，从而实现教学与生活的有效衔接。减弱数学的抽象性，便于学生学习和接受知识。比如，举办联欢会时教师可以让学生设计活动方案（如图5）。

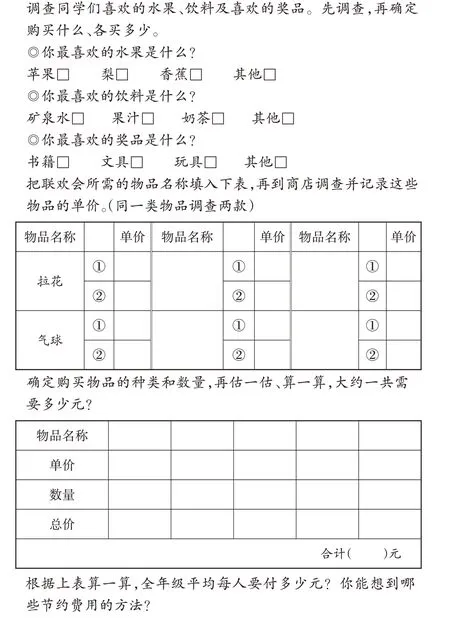
图5

这个方案涉及需要购买的物品、预计的价格、购买的数量、人均消费等信息，均以图表这样的非连续性文本的形式呈现出来。这样的活动体现了以学生为本的理念，有助于培养学生的消费观，同时能帮助学生养成做事周密的好习惯，提高学生做事的效率。

总之，在阅读非连续性文本时，学生能接触到大量、密集的信息，获得许多乐趣，同时能增加知识量和信息储备量，提高信息的利用率。非连续性文本阅读适应当今社会的发展，教学时，教师要指导学生审题，促进学生提高从非连续性文本中提取有效信息的能力。