以安全为导向的地铁过饱和线路跳站停车策略优化模型*

陶乐风 石俊刚▲ 杨 静 杨晓光

（1.华东交通大学交通运输工程学院 南昌 330013；2.同济大学交通运输工程学院 上海 201804）

0 引 言

地铁出行如今已是大多城市出行必不可少的重要通勤方式，随着客流规模的不断增大，很多城市（如北京、上海、广州、深圳等）均出现了客流拥挤现象，特别是高峰出行时段，大规模的客流聚集容易造成乘客踩踏、挤兑和屏蔽门夹人等事件的发生。疫情期间，客流聚集也会增加疫情传染风险，为地铁运营带来了较大的安全隐患。近年来，许多学者采取不同的运输组织方式来缓解地铁系统的客流拥挤问题，主要包括客流控制和行车计划优化2种方式。

客流控制方面，部分学者通过对车站采取协同限流策略来缓解地铁极端拥挤，即通过协同控制多个车站的客流进站速率，以减少站台客流聚集。其中，刘晓华等[1]以2 座相邻车站为例进行分析，得到了客流控制下2 座车站进站客流速率的计算公式。曾璐等[2]建立城市轨道交通网络客流分配模型，提出了限流车站备选集评价方法。赵鹏等[3]以乘客总等待时间最少和旅客周转量最大为目标，建立了考虑所有车站的客流协调控制模型。郇宁等[4]构建网络客流协同控制多目标优化模型，实现对有限运能的充分利用。姚晓平等[5]进一步将客流协同控制模型扩展到线网层面上。传统的客流控制大都以减少乘客等待时间或者客运周转量最大为目标，缺乏对于安全性的考虑，石俊刚等[6-8]则从安全角度，建立以客流聚集预警值最小为目标的地铁过饱和线路协同车站限流模型，提出了精细化的车站协同限流措施，实现在列车运载能力范围内提升运营安全。随后又将该方法扩展到线网层面上。还有部分学者从其他角度研究客流控制问题，如禹丹丹等[9]基于闭环反馈机制构建了车站主动式客流控制策略，融合客流密度短时预测实现客流的主动预防式调控，对车站实施精细化客流控制。Meng等[10]引入面向时刻表的时空网络表示方法，提出基于定制化出行的客流管控策略。温念慈等[11]则将协同矩阵与多目标规划理论运用到突发大客流下多车站协同客流控制应急决策研究中。虽然协同客流控制策略能够较好的缓解车站拥挤，但实际操作中需要多个车站进行协同配合，操作难度较大，目前在实际运营中还没有得到成熟应用。

行车计划优化角度，则是通过寻求更优的行车计划方案来提高地铁系统的服务水平。其中Niu等[12]、Wang 等[13]、Qi 等[14]、Zhao 等[15]、Gong 等[16]及Jiang等[17]根据动态乘客需求制定合理有效的行车计划。王智鹏等[18]、刘意[19]通过研究快慢车策略提高运输效率，缓解车站拥挤。但快慢车策略对线路设备要求较高，需要车站备有越行轨道，策略可移植性较差。还有研究考虑在列车发生延误甚至中断的场景下，通过跳停策略来减少乘客的等待时间、延误等，如Gao等[20]、王婵婵等[21]。此外，孟凡婷等[22]、杨陶源等[23]将客流控制策略与行车计划相结合，提出了2种策略的协同优化模型。可以看出，上述行车组织优化方面的研究主要以提高服务水平为目的（如减少乘客的等待时间、延误等），缺乏对于运营安全的考虑。而车站客流的极端拥挤，除给乘客带来延误外，过多的乘客聚集也会给运营带来风险。如何采用合理的行车调整，在保证乘客服务水平的同时，尽可能避免车站客流的过度聚集，是一项值得研究的问题。

从安全角度出发，通过考虑各车站随时间变化的动态客流需求，采用列车跳站停车策略为下游各拥挤车站合理预留列车容量（特别是高峰时段）以此均衡上下游车站的客流聚集数量，使得每个车站的乘客等待人数都处于较为安全的范围，同时尽可能保证乘客在站台上的平均等待时间。即在提升运营安全的同时，充分保证客运服务水平，并通过算例分析验证模型的有效性与可行性。

1 问题描述

高峰时段，市郊地铁线路出行存在明显的潮汐现象，出行流向较为集中，如早高峰大量客流由郊区流向市中心区域。此时，由于列车容量大部分被上游站乘客占据，在一些下游客流较大车站，列车容量有限，到达乘客无法及时登车，易引发过度拥挤现象，见图1（a）。以市郊地铁线路为研究对象，通过跳站停车策略，合理安排部分列车在上游车站不停站，减少上游车站的上车人数，从而预留部分列车容量以缓解下游车站的过度拥挤，见图1（b）。通过跳站停车策略，上游车站乘车人数减少，此时虽然上游车站增加了一定的等待人数，但下游过度拥挤车站的客流聚集将大大缓解，由此能够从线路整体层面提高安全性。同时，在安排跳站停车方案时，也会充分考虑乘客的服务水平。

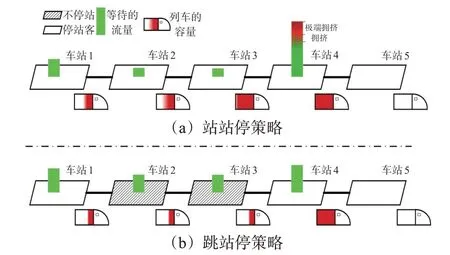
图1 站站停与跳站停策略的说明Fig.1 Illustration of the all-stop and skip-stop strategy

综上，本文所研究的问题是，在每趟服务列车中设置合理的跳站停车方案，使各车站乘客聚集总风险最低和乘客总等待时间最小。为了简化问题研究，制定了一些假设条件。

假设1。本文考虑随着时间变化的起讫点客流需求（dynamic origin-destination），即动态OD客流需求是提前给定的（基于历史数据或预测值），在这种假设下，乘客不会因为跳停策略改变或放弃他们的出行计划。

假设2。在每个车站，不同OD的等待乘客混合均匀。在这种情况下，当列车容量有限时，每个OD行程的上车乘客率等于这个OD 行程的等待乘客率。基于该假设，可以推导出在容量限制情况下的各OD上车人数，及后续列车在各车站的下车人数。

假设3。当列车需要停站时，进入和离开车站需要减速和加速。与不停站的列车相比，会额外损失部分行程时间。为了简单起见，在本研究中不考虑在车站减速和加速造成的时间损失，即假设列车在区间的运行时间均相同。Yang等[24]的研究中也做了相同的假设。

假设4。乘客均选择直达列车，不考虑通过快慢车中途换乘、反向迂回乘车的情形，即当该列车不在目的地车站停车时，乘客将会等待下一趟列车。

2 模型构建

为求得较好的跳站停车策略，本文建立相应的数学模型并设计符合模型特性的高效求解算法。建模过程中涉及的符号与索引见表1，中间变量见表2。

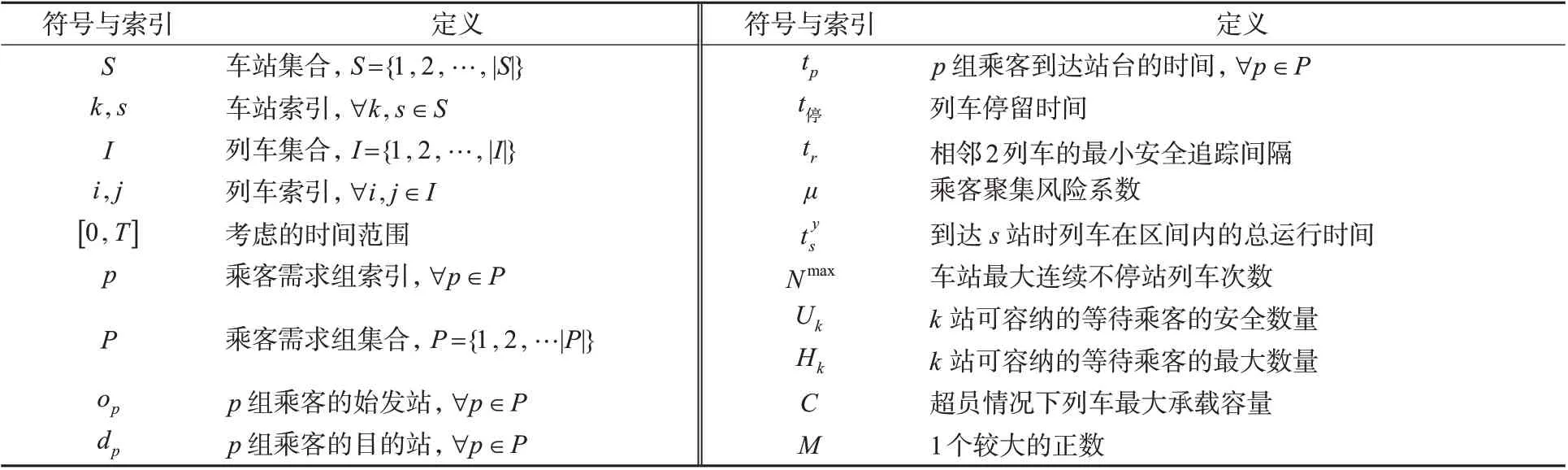
表1 符号与索引Tab.1 Symbols and Indexes

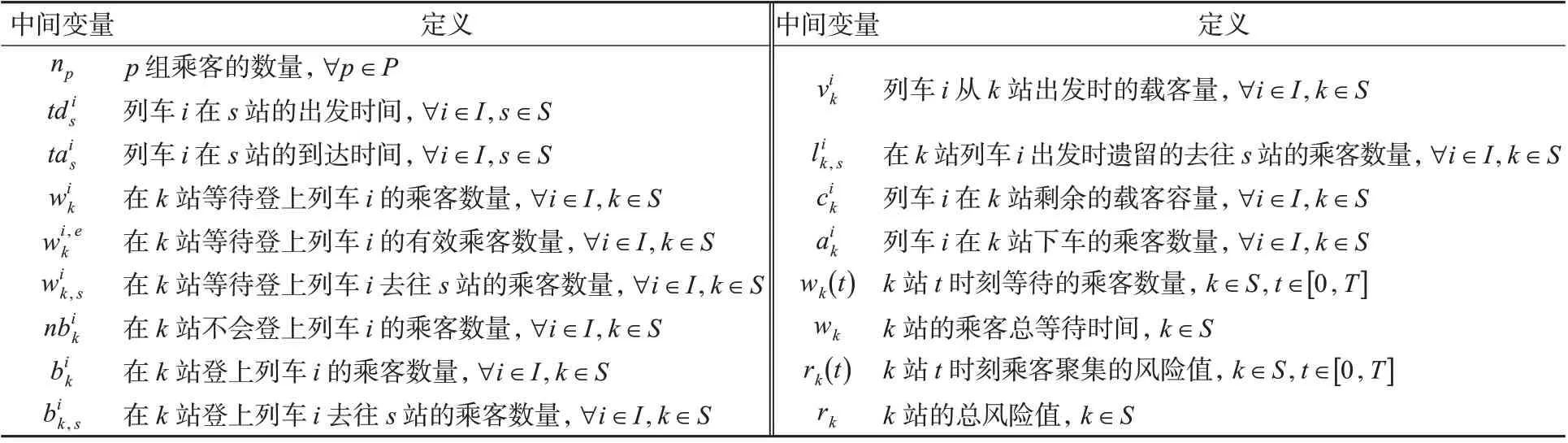
表2 中间变量表Tab.2 Indirect variables

决策变量为列车i在车站k是否停站，采用表示，如果停站=1，否则=0。

2.1 列车停站约束

连续在车站跳停，会造成乘客等待时间过长，降低服务水平。因此，需对车站连续跳停列车数进行限制，计算见式（1）。

2.2 列车时刻表约束

假设列车在区间的运行时间相同，因此可以根据列车在始发站的出发时间以及跳站停车策略推算出列车在各车站的到发时间，计算见式（2）～（3）。

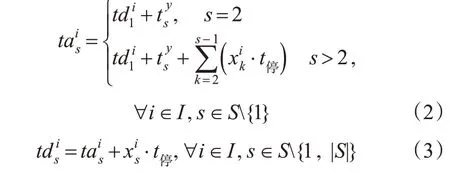
为确保行车安全，需保证相邻2 列车之间满足最小安全追踪间隔，计算见式（4）。

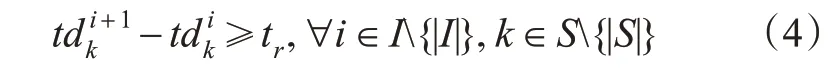
2.3 乘客加载约束

列车在各区间的载客人数是1 个动态变化过程，由列车在各车站的上、下车人数决定，计算见式（5）。

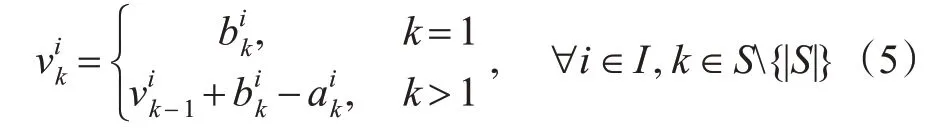
车站等待登车的乘客数决定由2 部分构成：①相邻2列车间隔内抵达车站的乘客数量；②上1列车未能载走的乘客数。计算见式（6）～（7）。

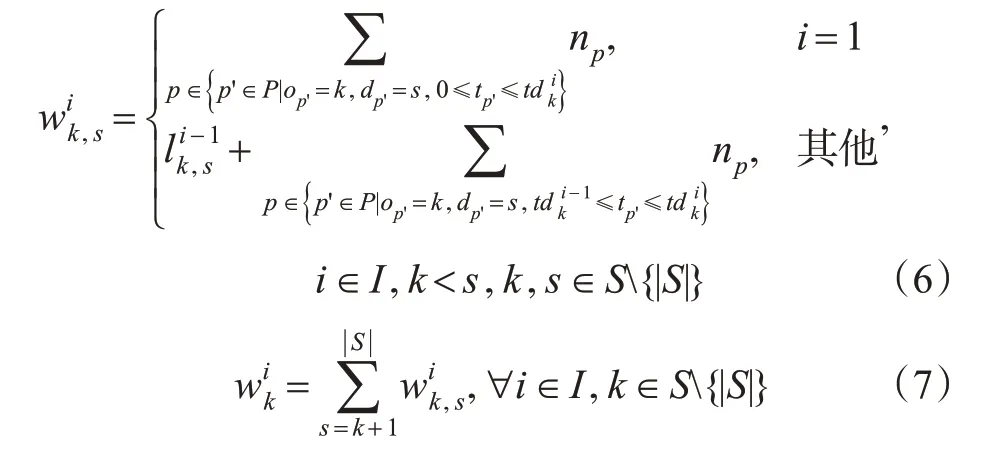
列车的上车乘客数受到列车剩余的容量的限制，与列车在上1 个区间的载客人数以及本站的下车人数直接相关。计算见式（8）。

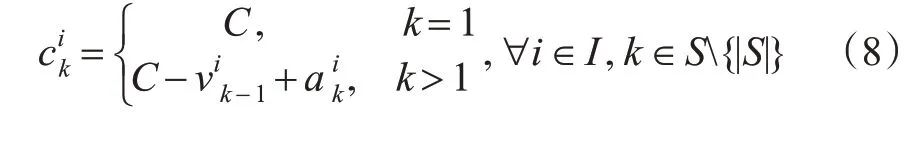
在列车跳站停策略下，只有在目的站停站，乘客才能上车。即如果列车在乘客的目的站不停站，乘客则不会登上该列车。因此，在计算上车人数时，需要考虑乘客的OD 构成。其中，等待的乘客中不能登车的人数，计算见式（9）。

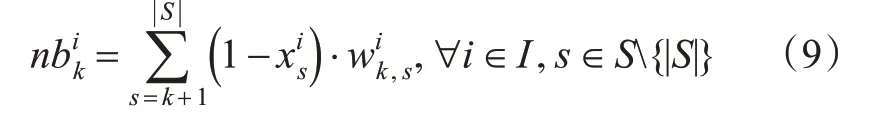
在等待的乘客中剔除掉一部分没有上车意愿的乘客，最终可求得有效的等待乘客数，计算见式（10）。

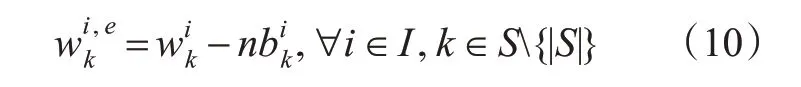
当列车在车站停站时，根据列车的剩余容量，实际上车人数计算见式（11）。

由于本文假设在等待过程中，不同OD 的乘客均匀混合。基于该假设，可以推导出上车人数中不同OD乘客的构成数量，计算见式（12）。

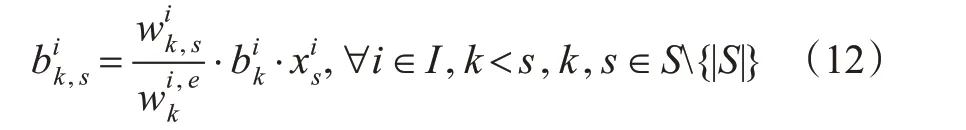
在容量限制因素下，列车遗留下来的乘客数，计算见式（13）。

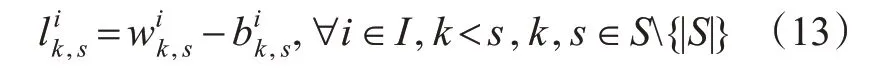
根据上车人数的OD 构成，可计算出各站下车的乘客数量，即以该站为目的站的所有登车人数之和。计算见式（14）。

在跳站停策略下，需保证所有乘客最终均能够被服务，即最后1 趟列车在各车站的遗留人数都为0。计算见式（15）。

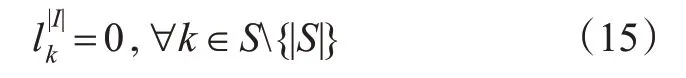
2.4 客流聚集风险函数与乘客等待时间

为推算各车站客流聚集风险，首先需要推算各时刻等待的乘客数，可由累积到达乘客减去累积上车乘客数量来计算，见式（16）。

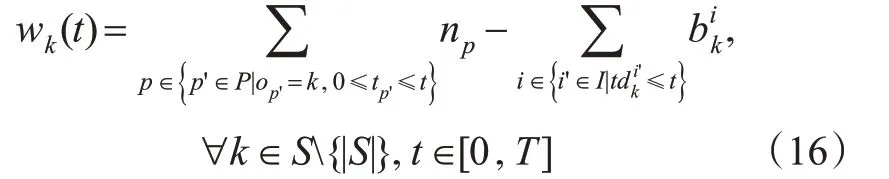
当车站的聚集人数到达一定规模时，会带来运营风险。乘客在k车站等待时间见图2，如果车站k的聚集乘客数超过Uk，则存在一定的潜在运营风险。此外，当累积乘客数量接近k站(即Hk)的最大容纳能力时，运营风险极大。为合理评估客流聚集风险，用rk(t)来度量车站k在时刻t的旅客聚集风险，计算见式（17）。

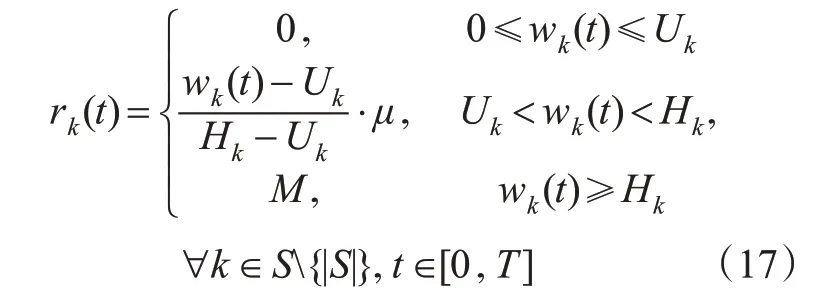
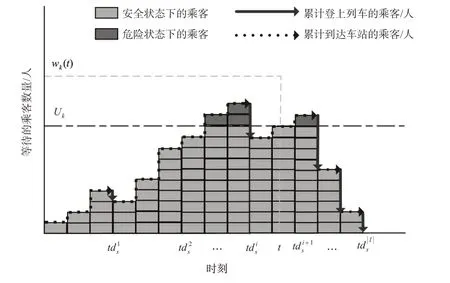
图2 乘客在k 车站等待时间Fig.2 The illustration of passenger waiting time at station k

车站k的乘客聚集总风险值需综合考虑聚集人数和客流的聚集时间。本文将连续的时间进行离散处理，离散的单位时间间隔为Δt，其中Δt为1 min，那么车站k的总客流聚集风险见式（18）。

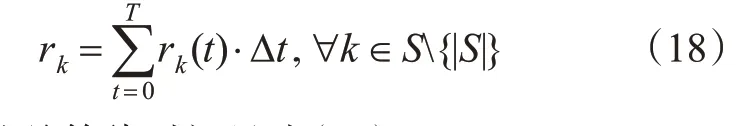
乘客的总等待时间见式（19）。

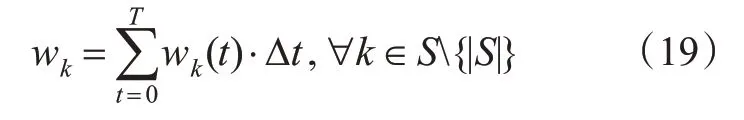
为降低线路客流聚集风险，同时保证客运服务水平，模型以总风险值最低和乘客总等待时间最小为双重目标。由于2 个目标存在不同量纲，故采用权衡系数θ1和θ2进行权衡处理，其中：θ1+θ2=1。综上，本文以安全为导向的列车跳停策略优化模型见式(20)。

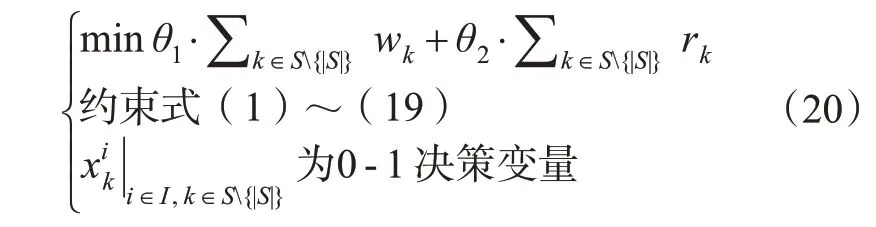
由于Δt为常量，不影响优化效果，因此在目标函数中可忽略该参数。

3 求解算法

模型中存在一定数量的非线性约束，如式（9），（11），（12），（17）。因此，所建立的模型为非线性整数规划模型，难以采用传统精确算法进行求解。为有效求解所构建模型，本文设计采用可变邻域搜索启发式算法（variable neighborhood search，VNS）进行求解。

VNS算法是局部搜索算法的推广，它通过在搜索近似最优解的过程中根据给定的规则系统地改变邻域结构，可避免算法过快陷入局部最优，具体步骤如下。

步骤1。在给定xi1=1（也就是首站必须停车）的前提下，根据车站与列车的数量随机生成1 组0-1初始停站方案c。

步骤2。在初始邻域中对初始解c通过给定的邻域结构进行局部搜索得到新的邻域解c*与对应的目标值f(c*)。

步骤3。通过给定的邻域结构变化求得局部最优值f(c**) ，如果局部最优值f(c**) 优于当前值f(c*)则接着将局部最优解c**更新为c并返回步骤2，否则程序将跳转到下个邻域中继续搜索。

步骤4。如果未满足搜索完所有的邻域R，则返回步骤2并将初始邻域更新为当前邻域。

步骤5。当搜索完所有的邻域R且满足给定的条件时输出最优解c**（较优的跳站策略），否则返回步骤2。

其中邻域结构也就是产生新解的方式有交换算子、变化算子、插入算子3种。

1）交换算子。通过在任意选择的2 列车之间交换跳停策略，获取邻域解。

2）变化算子。选择若干位置，对任意的列车跳站停策略进行改变，当=1 时就改变为=0，当=0时同理。

3）插入算子。通过插入任意选择的1 趟列车的跳站停策略。

值得注意的，当通过这3 种算子产生的新解可能会违反约束式（4），即列车安全行车间隔。为避免不可行解，在求解的过程中定义了1 个惩罚函数来惩罚可能违反约束式（4）的不可行解，见式（21）。

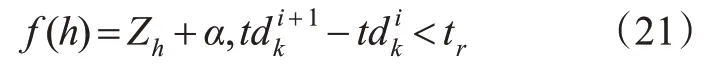
式中：Zh为模型的客观值，α为当获取的解违反行车间隔而设定的1个相对较大的惩罚值。因此在求解过程中一些不可行的求解策略将会尽量避免，提高了算法的效率，通过搜索，算法能在一定时间内获得较优的跳站停策略。

4 算例分析

4.1 基本数据

北京地铁八通线是1条全长18 km的城市轨道交通市郊通勤线路，连接着郊区和中心城区，中间没有换乘站，仅在两端有换乘站。见图3，地铁沿线共有13 座车站，沿市区方向分别编号为1～13（S={1,2,…,13}），考虑的时间范围是上午07：00—10：40，其中包括了早高峰时段和部分非高峰时段，涉及到下行方向的42 趟开行列车。在试验中使用的动态客流需求是由自动售检票系统（automatic fare collection，AFC）收集的2018 年6 月某工作日的乘客刷卡数据。

图3 北京地铁八通线线路Fig.3 Beijing Metro Batong Line Route

考虑到计算时间与迭代规模2 个方面的因素，通过多次试验调整得出结果较优的算法终止条件为：①最大循环次数1 000；②连续20 个循环内未获得改进解。试验相关参数和数据见表3，其中，车站站台的容量需进行实际现场调研来设定，为方便试验计算，将所有车站等待乘客安全数量阈值统一设定为2 000人，最大容纳乘客数为4 000人。

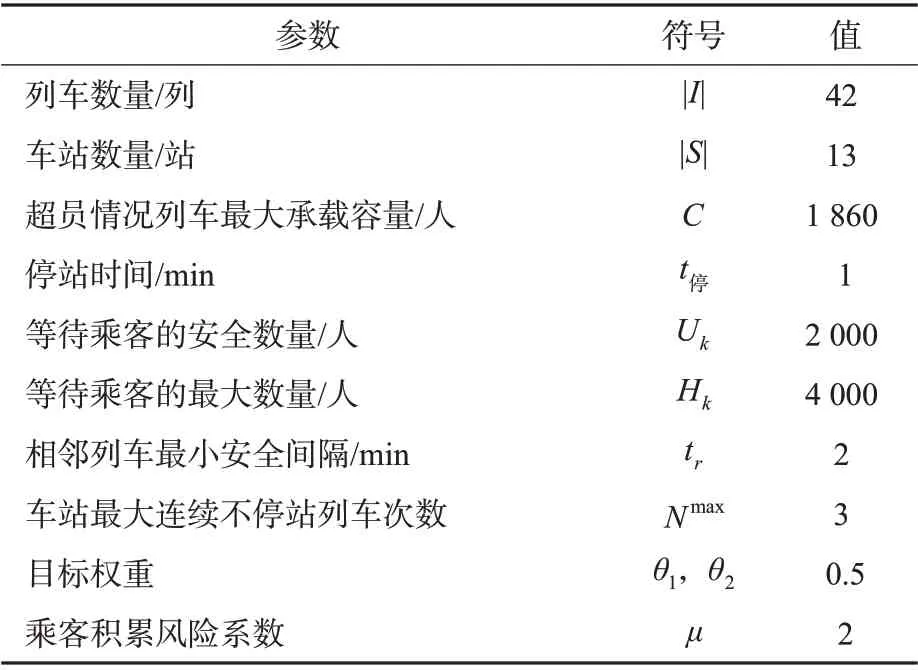
表3 求解参数Tab.3 Solving parameters

4.2 计算结果

4.2.1 跳站停车策略基础案例分析

基于上述数据，经过4.2 min 的计算，求得较优跳站停车策略，其中每个站列车跳站的总次数见表4。由表4 可见：为缓解下游站客流拥挤，大量列车在在上游车站采取了跳站停策略，预留了一定的车厢容量给下游拥堵车站。如在双桥站之前的大部分车站相对于双桥站及之后车站跳站次数要多，通过跳站停车策略预留的列车容量可以有效缓解下游极端拥挤车站的客流聚集。需要说明的是，一般6节编组的列车容量为1 460人/列，但考虑到在高峰情况下，列车会处于超员的状态下运行，最大的承载容量会高出定员容量20%～30%，为方便求解，将列车超员情况下的最大容量设定为1 860人/列。

表4 各车站跳站列车的编号和总次数Tab.4 Number and total number of skip-stop trains at each station

进一步分析跳停策略的效果，分别将采取和不采取跳站停策略的相关数据，见表5。

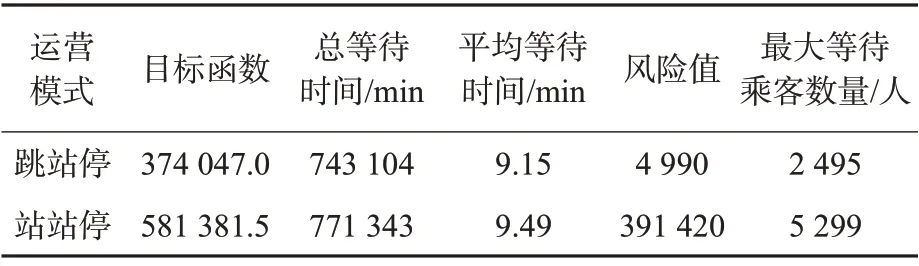
表5 站站停与跳停策略的求解结果Tab.5 Result of all-stop and skip-stop strategies solving

通过对比发现，采用跳站停车策略客流聚集的风险值大幅度降低，最大等待乘客数量也降到了安全阈值附近。同时，由于跳站停策略的影响，列车省去了部分车站的停站时间，相较于不采取跳站停策略来说在部分车站列车将会提前到达（尤其是拥挤的下游车站），乘客的等待时间也得到一定程度降低，即平均等待时间由9.49 min降低到9.15 min。

不同策略下，各车站的列车跳站停策略和客流聚集情况见图4。由图4 可见：常规停站策略下，双桥站和传媒大学站的乘客累积状态较为严重，尤其是传媒大学站。在极端状态下，大客流聚集在车站，给实际运营带来巨大风险，见图4（a）站站停策略。由于在站站停策略下，只要列车容量足够，乘客均可以上车，而上游车站等待的乘客拥有优先乘车权，因而在高峰时段，当列车到达双桥站和传媒大学站时，大部分列车基本处于满载状态。由于列车容量的限制，大量双桥站和传媒大学站的到站乘客无法登上列车，由此导致了极端拥挤情况。

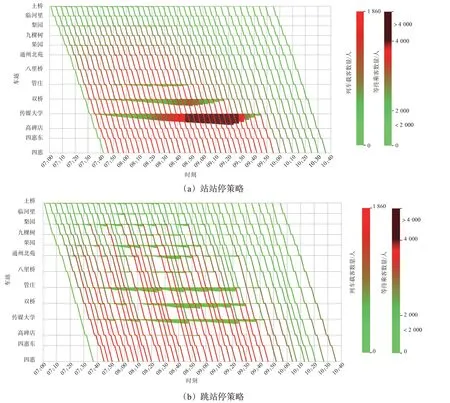
图4 不同情景下的停站策略与乘客等待数量Fig.4 Stopping strategy and waiting passengers volume under different situations

采用优化的跳站停车策略后，可以看到客流聚集的危险时间大幅降低，且各车站的客流聚集均处在较为安全的水平（见图4（b）跳站停策略），没有出现极端危险情况。虽然双桥站、管庄站和传媒大学站仍存在部分危险状态，但最大的乘客等待人数仅2 495 人，相对于常规停站策略已有较大缓解。同时需要指出的是，由于大量列车在上游车站跳站，导致上游车站出现一定的乘客积累，但均处于安全状态。通过对策略实施前后的对比分析可知，实施列车跳站停策略不仅能够缓解车站过度拥挤现象，同时也能够优化总体客运服务水平。

4.2.2 灵敏度分析

1）最大连续跳停列车数。当采取跳站停车策略时会存在某些车站多趟列车连续不停站的情况，这会增加部分车站乘客的等待时间，所以本文对车站最大列车不停次数进行了分析，从而为选择合适参数提供依据，详情见表6。

表6 车站最大列车连续不停策略Tab.6 Maximum continuous train strategy at the station

研究的目的是通过在上游车站尽可能的跳站来预留车厢容量给下游拥挤的车站。当策略1 实施时，列车必然在上游车站跳停次数少于策略2，此时上游乘客可乘车机会较大，列车预留容量的空间较小，无法有效缓解下游站的客流拥挤，虽然上游车站的乘客等待时间能够得到保障，但下游拥挤车站客流聚集风险值却大大增加，依然无法有效提高运营的总体安全性。

相对而言，策略2虽然能够提高运营安全性，但也会造成上游车站乘客过多等待，可能会增加乘客的投诉次数。因此，实际运营时需根据需求合理设置。

2）双目标权重系数。在模型的目标函数中同时考虑了与服务质量相关的乘客总等待时间和与运营安全相关的客流聚集风险值。在目标中，需通过权重系数在2 个目标间进行权衡。本文测试了6 种权衡系数的取值情况，θ1取值分别为0,0.2,0.4,0.6,0.8,1.0，各取值对应的计算结果见表7。

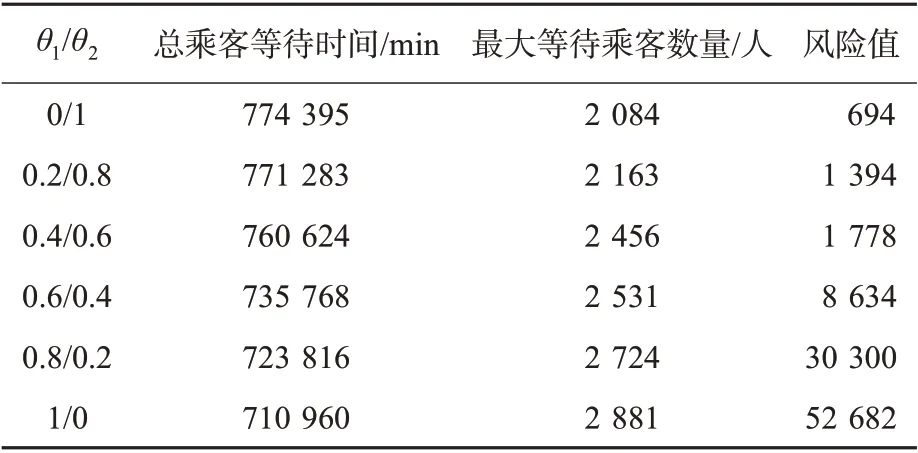
表7 权衡系数的取值Tab.7 The value of the trade-off coefficient

可以看出，当θ1增大时，乘客等待时间呈现出下降的趋势，同时相应的总乘客风险值增大，通过设置不同的权重系数，可以在安全性和服务质量上进行合理取舍，对实际运营更具意义。

5 结束语

针对过饱和地铁线路的客流过度拥挤问题，采取列车跳站停策略，以控制上游车站的上车乘客数，从而为下游拥挤车站合理预留车厢容量，以缓解过度拥挤现象。从系统优化角度出发，构建了列车跳站停优化的非线性整数规划模型，以最大限度地降低各个车站的乘客聚集风险和乘客总等待时间。针对该模型的非线性特性，设计了可变邻域搜索算法（VNS）以快速求解高质量跳站停策略。计算结果表明：采用优化的跳站停策略可以显著缓解客流过度拥挤现象，提高运营安全性。同时线路乘客总等待时间也有一定程度降低。

此外，在现有研究基础上还可以进一步研究的方向包括：①在未来的研究过程中可以考虑将单一的地铁线路扩展到网络之中；②本文客流需求是常量且预先给定，在后续研究中可考虑随机客流需求，进一步探究鲁棒性列车跳站停策略。