城际铁路列车停站方案的遗传算法求解

高明瑶，石红国

（西南交通大学 交通运输与物流学院，四川 成都 611756)

0 引言

城际铁路是服务于相邻城市间旅客的铁路。近年来，我国城市群快速发展，相邻城市间的人员交流增多，城际铁路成为相邻城市间旅客出行的重要交通方式。相比普速铁路，我国的城际铁路在服务质量与服务水平方面提升较大，但仍然面临城际高速公路客运的强有力竞争。优化城际铁路列车停站方案可以提升城际铁路列车的竞争力，提升城际铁路在相邻城市间客运市场的客流分担率。

国内外学者对列车开行方案问题进行了大量研究。史峰等[1]从铁路运输企业和旅客利益出发，研究客运专线旅客列车开行方案的多目标优化模型及求解方法。张旭等[2]以丹大城际铁路为背景，以运营收益最大、旅客候车时间最小和列车空费能力最小为目标函数，采用遗传算法求解。牛丰等[3]分析长途客流输送的直达模式和中转换乘模式，综合分析不同列车种类的直达模式，提出中转换乘模式客流输送方案的优化方法。曹志超等[4]基于越行站滞留旅客数量，提出列车停站方案的双目标非线性混合整数规划模型，采用禁忌搜索算法求解。牛丰等[5]构建不确定客流条件下高速铁路列车停站方案设计的机会约束规划模型，采用Gurobi 求得最优列车停站方案。刘璐等[6]针对高速铁路旅客出行时空敏感性较高的特点，构建三维时空状态网络，建立基于旅客出行需求的停站方案与列车运行图综合优化0-1 整数规划模型，并设计拉格朗日松弛算法求解。闫海峰等[7]考虑高速铁路列车客流需求与技术条件，以列车运行线占用时间最少为目标，建立非线性0-1 规划模型，采用Lingo 求解。唐禄林等[8]针对快慢车的越行特点，分析城市轨道交通乘客出行时间和企业运营成本，构建城市轨道交通快慢车模式下的停站优化模型，采用遗传算法求解。

针对城际铁路列车停站方案问题，以铁路企业运营收益最大和旅客出行成本最小为目标函数，以车站服务频率、设备能力、列车停站次数等作为约束条件，建立城际铁路列车停站方案的多目标混合整数规划模型，设计基于理想点法的城际铁路列车停站方案遗传算法，求解铁路企业收益与旅客出行成本相对符合预期的城际铁路列车停站方案。

1 城际铁路列车停站方案优化模型

1.1 模型假设

常见的城际铁路列车停站模式有“大站停”“择站停”“站站停”3 种。在设计停站方案时，应实现多种停站方式相互配合与协调，形成最优的停站方案。借鉴史峰等[1]的思路，对城际铁路列车停站方案问题作出以下基本假设。

（1）列车运行方向假设。城际铁路列车的停站方案对应某一特定的列车运行方向。为方便阐述，选择下行方向为研究方向，假设不考虑运行方向对不同停站类型列车的影响。

（2）封闭性假设。在制订停站方案时，只考虑本线客流，不考虑跨线和换乘客流。

（3）确定性假设。在编制停站方案时，假设列车的起讫点、运行径路、编组等已经确定。

1.2 符号说明

设Q= {B，Z，A}表示3种列车停站模式的集合，其中B为“大站停”模式，Z为“择站停”模式，A为“站站停”模式。设W为上述3 中停站模式中的1 种，有W∈Ω，该种模式的城际铁路列车1 次停站成本为SW，单位距离运行成本为RW，单位运价率为pW，按该模式停站的列车数量为N W。M为车站集，i，j为车站，i，j∈M。dij为车站i到车站j的距离，D为城际铁路线路起讫车站之间的距离。为在车站i与车站j之间，选择停站模式W列车的客流量。为乘坐W模式的列车k，在车站i上车，去往车站j的旅客数量。表示停站模式为W的列车在车站h的停留时间。决策变量= 1表示停站模式为W的列车k在车站h停站，= 0表示停站模式为W的列车k在车站h不停站。

1.3 目标函数

停站方案优化目标为最大化城际铁路总运营收益和旅客总出行时间最小。

（1）最大化城际铁路总运营收益为

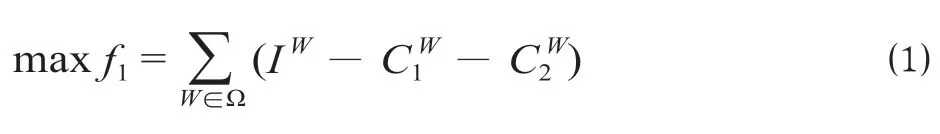
式中：f1为城际铁路总运营收益；IW为停站模式W的列车总客票收入；C1W为总停站成本；C2W为总运行成本。

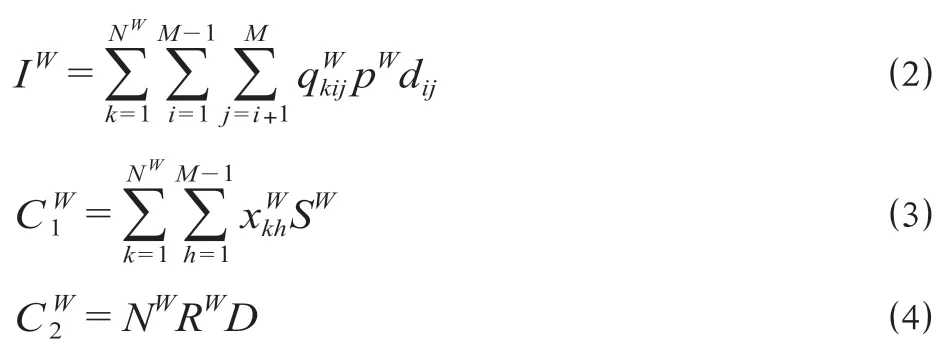
综上，最大化城际铁路总运营收益为

（2）最小化旅客总出行时间。对于城际铁路列车，起讫点固定后，同一OD 间旅客的出行时间只与列车的总停站时间有关，因而将旅客总出行时间最少的目标转化为总停站时间最少的目标，即

式中：f2为总停站时间。

1.4 约束条件

（1）车站的服务频率约束。车站有一定的服务频率要求，在某车站停站的列车数不能低于给定的下限，即

式中：nh为车站h停站的最少列车数。

（2）车站设备能力的约束为

式中：eh为在车站h停站的最大列车数。

（3）列车停站次数的约束为

式中：l W为W模式列车的最少停站次数；gW为W模式列车的最大停站次数。

（4）客流条件约束。从车站i出发的W模式所有列车能够运输的总旅客数不小于车站i到车站j的W模式列车的客流量，即

（5）变量取值范围的约束。考虑到所有列车在起讫点车站必须停车，因而的取值为

2 城际铁路列车停站方案的遗传算法

2.1 多目标转化为单目标的理想点法

采用理想点法将上述多目标混合整数规划模型转化为单目标模型。以多目标fi在上述模型中输出的最优值为分量，生成向量= (f1*，…，fn*)，由于所研究问题是一个多目标问题，考虑采用欧几里得距离评价法将多目标转换为单目标问题。构建以下评价函数

公式 ⒀ 表示各个可行方案到最优方案的欧几里得距离，该距离直观上表现为任一方案较最优方案更劣的程度，方案的该距离越小，则表示该方案更优。原模型转化后的单目标优化模型为

2.2 城际铁路列车停站方案遗传算法

城际铁路列车停站方案优化问题是大规模组合优化问题，鉴于上述混合整数规划模型的计算复杂度，采用遗传算法求解转化后的单目标模型。遗传算法流程如图1 所示。

遗传算法的具体求解步骤如下。

步骤1：编码及初始种群生成。城际铁路列车线路上的每1 列车都用1 个染色体表示，染色体的数量即为城际铁路列车的数量，每个基因位都与线路上每1 车站相对应，染色体长度即为车站数量，基因位i取值为0 表示列车在第i站不停站，取值为1 表示列车在第i站停站。随机生成初始种群。设置迭代次数t= 0。

步骤2：解码及染色体有效性检验与修正。在生成初始种群和遗传进化过程中，可能产生不满足上述约束条件的无效染色体，此时，该无效染色体由步骤1 中生成的染色体种群中1 个新的染色体替换，按初始种群的形成机制重新随机生成。

步骤3：计算适应度函数。选取公式⒁中的单目标函数为适应度函数，适应度函数取值越小，表示方案越好，即个体适应度越好，则该个体被选择复制进下一代的概率越大。

图1 遗传算法流程Fig.1 Process of the genetic algorithm

步骤4：新种群生成。①遗传算子。选择算子采用排序选择策略，将群体中的个体按照个体适应度值升序排列并均分成10 组，最后1 组的个体用第1 组的个体替代，保证每代进化过程中适应度好的个体被复制到新的种群中去，且种群规模不变。②交叉算子。采用两点交叉的方法，将种群中的个体随机两两匹配，再按照均匀分布随机参数交叉位置，以概率pc交换两点之间的基因值并产生新的个体。两点交叉操作如图2 所示。③变异算子。采用单点变异的方法，按均匀分布随机产生变异点位置，以概率pm对基因值进行变异操作产生新的种群。单点变异操作如图3 所示。

图2 两点交叉操作Fig.2 Two-point Crossover

图3 单点变异操作Fig.3 One-point Mutation

步骤5：迭代次数t=t+ 1，判断程序终止条件。如果达到最大迭代次数则终止程序，否则返回步骤2。

3 算例分析

3.1 问题生成

随机生成6 个城际铁路车站，各个站间客流OD 量在[0，500]间随机生成，得到城际铁路站间下行方向客流OD 分布如表1 所示。

表1 城际铁路站间下行方向客流OD 分布 人Tab.1 OD distribution of down direction between stations

假设所有的客流OD 量中，有30%的乘客选择“大站停”列车，30%的乘客选择“择站停”列车，剩余40%的乘客选择“站站停”列车。根据该比例以及表1 所示的客流OD 分布，可得到乘坐各种停站模式列车的OD 间客流量。

各个车站的站间距如表2所示。根据实际情况，设车站服务频率不小于3 列，车站设备能力不大于20 列。

表2 各个车站的站间距 kmTab.2 Distance between stations

3.2 问题求解

设置遗传算法的相关参数。其中，种群规模为20，交叉概率为0.8，变异概率为0.1，最大迭代次数为100，利用遗传算法求解，得到城际铁路列车停站方案如表3 所示。停站方案中，“大站停”列车共停靠5 站，“择站停”列车共停靠3 站，“站站停”列车共停靠14 站，停站方案共6 种。

表3 城际铁路列车停站方案Tab.3 Intercity train stop scheme

4 结束语

由于列车停站方案优化问题的复杂性，需要考虑经济社会等多方面因素，很多问题尚待深入研究。由于城际铁路中部分车站等级较高，应优先考虑大站停列车停站方案。另外，除了以最大化铁路部门运营收益和最小化旅客出行时间为目标函数外，还可以将最大化列车满载率作为目标函数，充分利用列车运能，减少能力虚靡。