考虑冲突规避的自动化集装箱码头AGV 优化调度方法*

丁 一 袁 浩 方怀瑾 田 宇

（1.上海海事大学物流工程与科学研究院 上海 201306；2.上海国际港务（集团）股份有限公司 上海 201306）

0 引 言

自动化导引车（automated guided vehicle,AGV）作为自动化集装箱码头的水平运输机械，对于提高整体码头作业效率有着至关重要的作用，因此AGV调度优化问题一直是港航领域的热点问题。AGV的调度有3个层面：AGV任务分配、AGV路径规划、AGV交通控制，在运筹优化领域一般只考虑任务分配和路径规划[1]。

AGV 调度优化问题一直是学者关注的热点问题。早期对于该问题的研究只考虑任务指派或者路径规划中的1个方面。任务分配的目标在于分配任务给合适的AGV 并决定作业顺序。根据任务信息在调度周期内是否可变分为静态和动态2 种，静态策略是在已知任务序列的前提下进行任务派发，以最小化成本或者最小化最末任务作业时间为目标，考虑AGV作业限制如充电、载重等因素构建混合整数规划模型[2-3]求解出任务分配方案；动态策略是根据当前AGV 的位置信息和新增任务信息进行任务派发，如基于竞价概念的任务分配或是针对不确定环境的任务分配调整[4]。AGV调度除了决定作业序列，还需要规划作业路径，受自身体积、道路容量、码头布局和行驶路径等因素的影响，作业过程中可能会出现冲突、死锁等问题，因此AGV 路径规划的目标在于寻找AGV 执行任务的无碰路径。根据环境信息是否已知可分为局部路径规划和全局路径规划。局部路径规划方法有粒子群算法，人工势场法[5]，多应用于仓库或更开放的环境。自动化码头的AGV多是在已知码头环境下的全局路径规划，主要规划算法有A*、Dijkstra、Floyd等[6]。除了路径搜索，冲突规避问题也是AGV路径规划中的重点和难点，Lyu 等[7]将Dijkstra 算法与遗传算法结合，规划全局最短路径的同时规避冲突，张中伟等[8]提出了不同冲突类型的时间窗模型并结合动态优先级来解决路径冲突问题。

早期的文献中对AGV调度的研究多为AGV任务调度优化，不考虑AGV 执行任务的路径规划问题。因为任务分配和路径规划在AGV 调度的重要性和相关性，有一些学者在任务分配的约束条件中规避AGV 间的冲突，并提出了基于无冲突路径的AGV 任务分配问题（dispatching and conflict-free route problem, DCFRP）。Krishnamurthy 等[9]基于该问题构建了混合整数规划模型，并使用了列生成算法求解。Correa 等[10]将柔性制造车间的调度主问题（即调度问题）建模为约束规划问题，将子问题（即无冲突路由问题）建模为混合整数规划问题，用CPLEX 求解了小规模的算例来验证模型的有效性。余娜娜等[11]以最小化最末工作的完工时间为目标，综合考虑了自动分拣仓库任务分配和路径规划，并提出了1 种在线协同算法实时调度AGV。Keisuke 等[12]考虑了AGV作业特点并基于时空网络对AGV 进行调度，并提出了1 个有效的不等式来减少运算时间的算法，可以看到，目前对于AGV 综合调度的研究多集中于柔性车间或者仓库。

与车间或者仓库比，自动化码头水平运输作业区域广，AGV 数量多且作业量大，因此涉及到的作业顺序安排和随机路径决策问题更为复杂，仅考虑AGV 任务分配而不规划路径会导致AGV 作业路径存在大量冲突。部分学者针对自动化码头的AGV综合调度问题进行了研究。Hu 等[13]结合预规划算法和实时规划算法的优点，提出了1 种三阶段分解算法，将A*算法与时间窗原理相结合，按时间顺序规划每个AGV 的路径并规避冲突。李静等[14]以最小化AGV能耗为目标设计了两阶段算法，第一阶段基于最短路径优化AGV调度，第二阶段基于冲突更新集装箱AGV调度。Ji等[15]先建立集成调度问题的双级编程模型，上层模型是3种设备的集成调度，下层模型是AGV的无冲突路径规划，接着基于冲突解决策略设计了2种双级优化算法。然而目前针对自动化码头AGV调度的研究仍旧较少。

梳理AGV调度相关研究，目前对于自动化码头AGV 调度系统相研究存在如下问题：①多数AGV调度的研究未能综合考虑任务分配和路径规划问题；②未能考虑路径规划和任务分配的相互影响，路径规划冲突规避后未能考虑调整不合理的任务分配；③缺少对于自动化码头等待区域的研究；④缺少对于AGV集中作业的拥堵情况下AGV调度策略和路径规划的研究。

鉴于此，对考虑冲突规避的自动化码头AGV调度问题进行研究，结合AGV作业流程和自动化码头布局特点，综合考虑了AGV任务分配和路径规划的相互影响，保证AGV 资源和路网资源配置的合理性，在追求作业成本最小化的同时确保多AGV间路径无冲突。

1 问题描述

AGV 作业环境有仓库和集装箱码头。自动化码头对比仓库或者车间具有车道数多，AGV 数量多，作业繁忙等特点。自动化码头布局见图1，由堆场作业箱区，陆侧装卸区，AGV等待区，海侧装卸区等组成。AGV作业分为进口箱作业和出口箱作业，出口箱作业由堆场机械抓取指定集装箱到AGV 上由AGV运输到海侧，桥吊将AGV上的集装箱装载到指定贝位，进口箱作业则相反。为了避免AGV和桥吊或堆场机械相互等待的情况，在堆场和岸桥处均设有缓冲区暂时存放集装箱。为了避免作业冲突，若AGV的目标桥吊位置有AGV在进行装卸作业，在从海侧到陆侧或陆侧到海侧时在等待区等待前1辆AGV作业完成。

图1 自动化码头布局Fig.1 The layout of automatic port

任务分配和路径规划均会影响AGV 作业效率。任务分配不合理会增加AGV行驶距离；路径规划不合理会使得AGV 作业时需要频繁的等待以规避冲突，严重时甚至会出现“死锁”问题。因此对AGV 的调度需要合理的任务分配和路径规划减少总作业时间和路径冲突带来的等待时间。

分2 个阶段研究自动化码头AGV 调度问题，第一阶段根据任务位置和作业时间分配任务给AGV并决定作业顺序，第二阶段根据任务分配的结果在规避冲突的基础上规划路径，针对拥堵问题，规避冲突后重新计算任务执行的代价矩阵输入第一阶段模型再次进行任务分配，不断迭代直到生成路径规划无冲突的任务分配方案。

2 模型构建

2.1 基于自动化码头作业特点的AGV 任务分配模型

任务分配模型为AGV 决定任务序列。自动化码头作业中，AGV 1 次可装载1 个40FEU 和2 个20TEU。AGV 作业流程见图2，AGV 在完成上一任务后根据目前的电量和载重情况决定是否执行下一阶段的作业任务。部分文献为了简化模型不考虑AGV的多载和电量等因素，将任务分配看成m：n的指派问题。为了贴合自动化码头AGV的作业特点，将单个运输任务精确到装载和交付的具体操作，同时考虑了AGV多载和电量约束，因此该模型会比一般的任务分配模型复杂，可以看成是带时间窗的装卸货问题（pickup and delivery problem with time window，PDPTW）求解。第一阶段的模型为各个AGV决定任务序列，以最小作业成本为目标完成所有水平运输任务。任务用最早开始时间ai，最晚完成时间ei，生成节点i和目标节点n+i来描述。

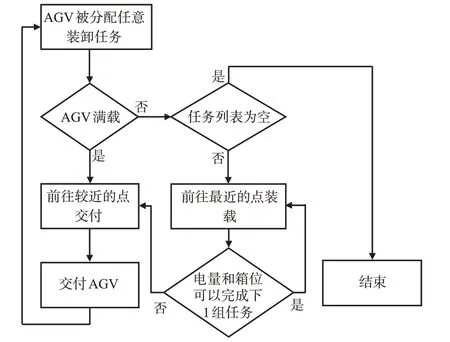
图2 AGV作业流程图Fig.2 AGV operation flowchart

模型假设如下。

1）AGV运行速度恒定。

2）AGV从充电站出发，电量不够完成任意1组取送货任务时返回充电站。

3）AGV在装载交付任务中不消耗电量。

4）AGV 耗电恒定，满电状态下运行总距离、总时间相同。

5）AGV0时刻从充电站o出发。模型参数见表1。

表1 任务分配模型参数表Tab.1 Theparameters ofthe task allocation model

决策变量：xijk表示当AGVk访问任务节点i后是否访问任务节点j，访问时为1，否则为0。

目标函数

约束条件

目标函数式（1）是最小化AGV 总运行时间，本文用作业时间来衡量作业成本；式（2）保证完成装载任务i后必须进行交付任务n+i；式（3）保证所有车辆从初始节点充电站出发；式（4）保证所有车辆最后回到充电站；式（5）是流量守恒约束；式（6）保证每个任务必须被执行且仅执行1次；式（7）为时间平衡约束；式（8）保证装载任务必须在交付任务之前；式（9）为电量平衡约束；式（10）表示只有当AGV的电量至少可以满足装载和交付任务才会被分配任务；且AGV 完成某一项任务后的电量应该大于安全电量即可以返回充电站；式（11）为任务时间窗约束；式（12）为载重量约束。

2.2 基于时空网络的AGV路径规划

上述任务分配模型决定AGV的任务序列，路径规划模型为AGV执行任务规划的路径，并保证路径间无冲突。路径规划需要对车间环境建模，常见的方法有：栅格图和拓扑图。作为高效的电子地图建模方法，拓扑图将AGV 的装卸作业位置，停车位置等抽象成点，路径抽象成边。传统码头或者仓库的路网拓扑图见图3（a），其中黑色区域表示堆场或者货架，AGV 可以深入堆场和货架，在路径上的任意点进行装卸作业。自动化码头构建路网拓扑图见图3（b），自动化码头主要作业区域集中在码头前沿，较少涉及堆场。

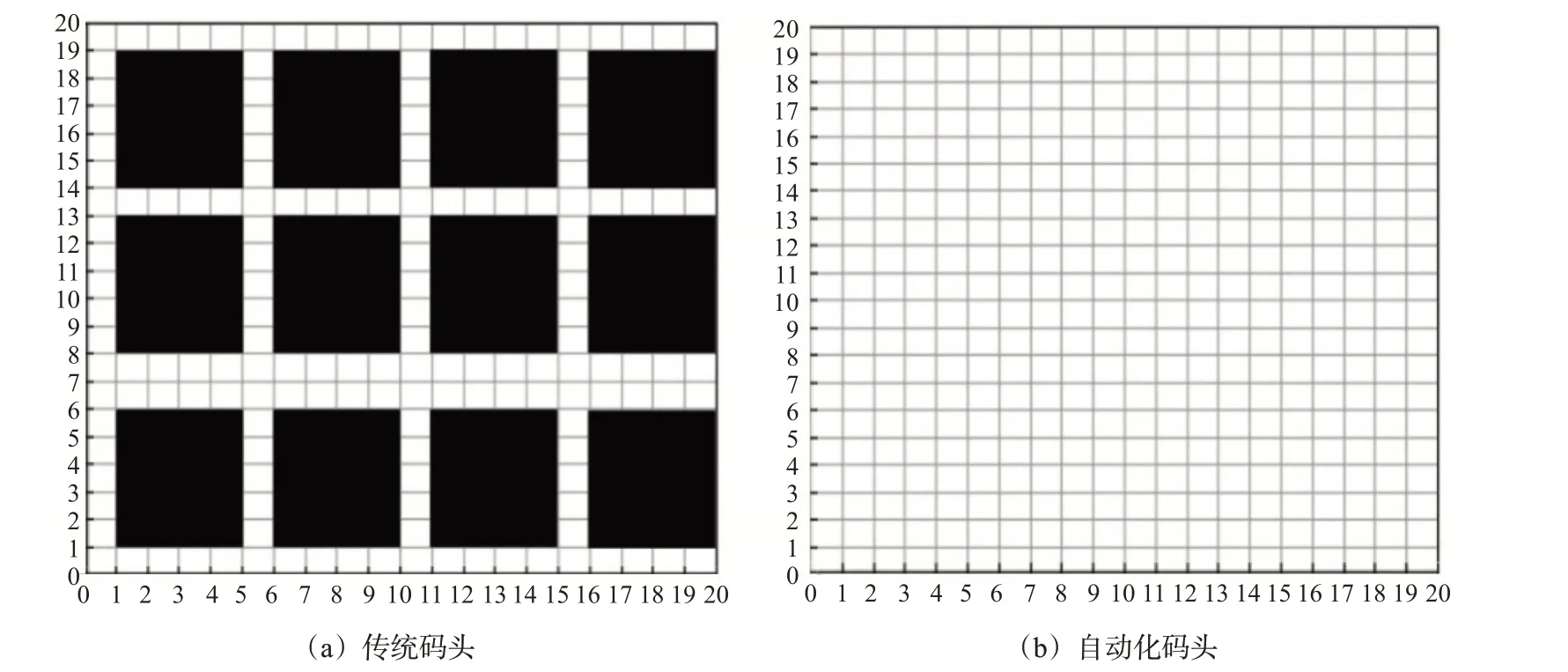
图3 传统码头和自动化码头路网示意图Fig.3 Schematic diagram of traditional wharf and automated wharf road network

现有文献大多将车间环境如码头或仓库抽象成二维路网进行路径规划，在不考虑其他AGV路径的前提下找到A点到B点的最短路径，规划完所有路径后针对不同的冲突类型解决冲突。然而，这种方式不适用于自动化码头。自动化码头AGV 作业位置集中在海侧和陆侧，水平运输区域空旷，路径上的障碍多为来自其他AGV 的动态障碍。因此需要实时检测路径冲突并进行规避。如图4 所示，将自动化码头离散成路网采用普通A*或Dijkstra算法得到的路径在网格图A点到B点中只有1 和2 这2 种路线，C点到D点只有3和4这2种路线。因此传统算法下，AGV 路线会存在同质化，作业时易出现大量路径冲突。同时作业区域集中在两侧，AGV停留作业在此处集中会带来“拥堵”问题。

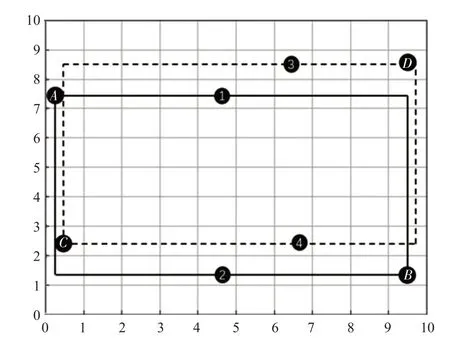
图4 普通A*或Dijkstra路径规划结果Fig.4 Result of Dijkstra orA*path planning

时空网络（TSN），是在空间信息的基础上添加时间信息构建的网络，见图5。TSN由节点及节点之间连接的边组成，每个节点代表特定时间的特定位置，每条边对应时间和可能的空间转换。时空网络记录了AGV 在不同时段能到达的多个位置和多个可行路段。时间线连接不同的节点以表示AGV 整个运行路径，每个时间线都包含开始节点和到达节点，上一时间线的到达节点是下1个时间线的开始节点，通过多个时间线不间断连接来表示AGV运行的时间连续性，由此可以对AGV路径进行时空分析。

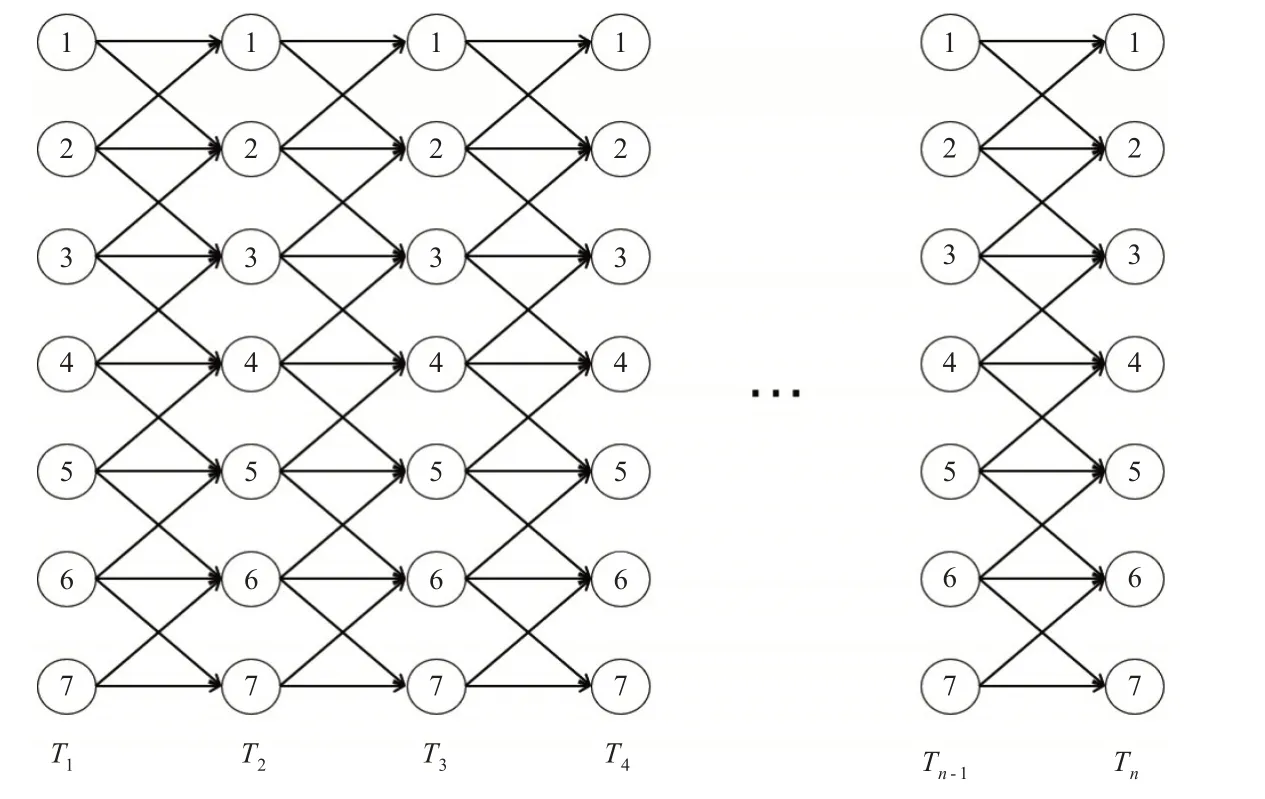
图5 时空网络模型Fig.5 Spatiotemporal network model

时空网络可以实时检测AGV 的状态信息和冲突路段，因此基于时空网络的路径规划可以使AGV在规避冲突的前提下规划路径。因为时空网络每1个节点和边包含时间属性，避免不同AGV遍历相同节点和边达到了规避多AGV 间的路径冲突的目标。模型参数见表2。

表2 路径规划模型参数表Tab.2 The parameters of the path planning model

决策变量：zkmnt表示AGVk在t时刻是否开始经过弧mn，经过为1，否则为0；ykmt表示AGVk在t时刻是否在节点m，在为1，否则为0。

目标函数

约束条件

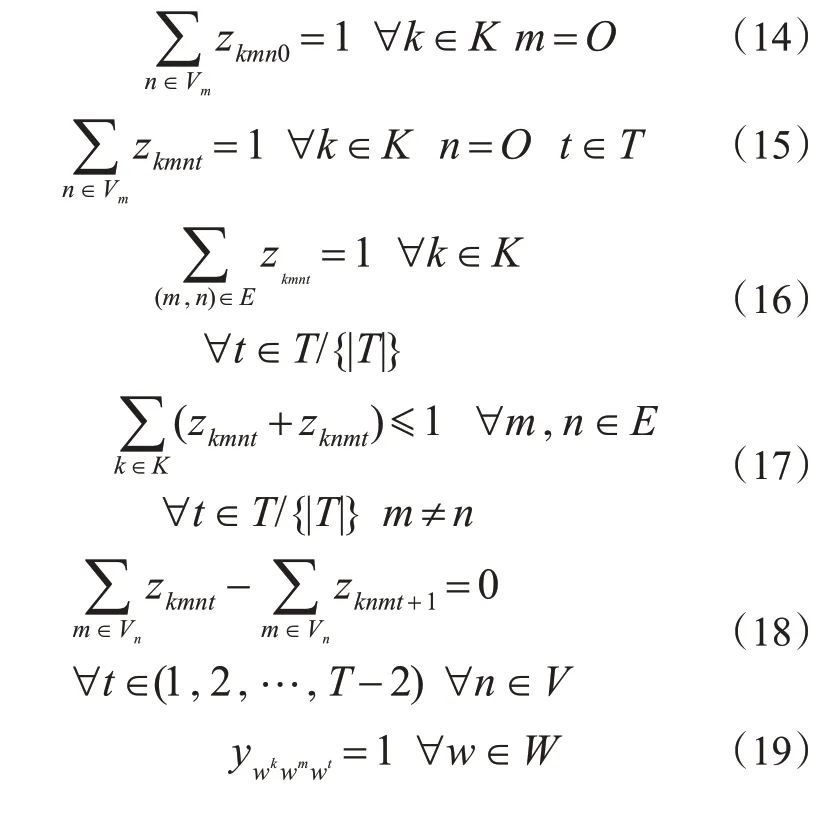
因为模型需要找到可行解，所以目标函数式（13）是常数，旨在寻找无冲突路径规划的可行解；式（14）保证所有的AGV最初均在初始节点；式（15）保证所有AGV最后回到初始节点；式（16）保证每个时刻AGV 只处于1 个位置；式（17）为避免相向碰撞约束;式（18）为流量守恒约束；式（19）为所有的任务都在正确的时间节点被执行；式（20）确保同1个时刻1个位置只有1台AGV。

3 算法设计

3.1 任务分配和路径规划算法设计

3.1.1 任务分配求解算法

任务分配问题类似于PDPTW问题，属于典型的NP-Hard 问题。为了快速求解，根据问题特点提出了2 阶段的快速模拟退火算法，该算法有效避免了无效插入，加速算法收敛[18]。模拟退火算法（SA）被证实有概率收敛到全局最优，其结果不依赖于初始解的好坏，有较好的鲁棒性，缺点在于收敛速度慢。为了保证解的质量和多次迭代的稳定性，这里采用模拟退火算法对初始解进行改进。

1）初始解生成。从未被安排AGV的任务列表中随机选出1 个组任务（装载任务Pi和交付任务Di）插入现有AGV 任务序列中，使得执行该组任务的代价最小且满足载重约束和时间窗约束。若该任务没有可插入的位置，则分配1 台新的AGV 给该任务，L中删除该任务；直到列表L为空时，输出结果，否则继续插入任务。

2）生成新解。新解产生的方式采用的是Remove和Insert过程。

Remove 过程：设置当前解为w，选取当前解w中AGV 任务列表中的任意任务（Pi和Di）移除。优先选取执行该任务对于此台AGV 时间过长的任务(减少总行驶时间)以及任务数较少的AGV中的任务（减少车辆数），抽出的任务组成集合c1和c2。

Insert 过程：将集合c中的任务重新插入形成新解w'。将任务数较少的AGV 序列c1中选出的任务分配给任务数较多的AGV；将c2中执行代价高（行驶时间长）的任务分配给插入代价最小的AGV。

3）计算新解f(w'),若f(w')＜f(w),接受新解，否则以概率e(-ΔT/T)（Metropolis准则）接受w'作为新的当前解w。

4）判断迭代次数是否达到该温度下的最大迭代次数，未达到则继续迭代，达到则降低温度进行新一轮的迭代，直到降低到设定的温度，输出最优解。模拟退火算法参数设置初始温度T0=2 000 ℃，α=0.99，每个温度迭代次数n为1 000，终止迭代温度为0.01 ℃。

3.1.2 路径规划求解算法

时空网络模型可以建成混合整数规划模型求解，但随着任务数量的增加会减慢计算速度。因此我们采用NETWORKX建立时空网络进行路径规划的算法[19]，该算法可以显著加快求解速度。时空网络中，每个节点用坐标x，y和时刻T表示，边的权重属性用该节点到达下1个节点时间表示。路径规划时根据任务的起始节点和目标节点构造t层时空网络，基于该时空网络执行最短路径算法进行路径规划。

对于冲突规避，目前文献中对路径规划的研究是基于二维路网寻找起点到终点的最短路径，完成所有任务的寻路后再处理路径中可能出现的冲突[15-16]。如图6所示，AGV路径冲突的类型有相向冲突，节点冲突，占位冲突，追赶冲突4种，根据不同的冲突类型提出不同的规避方案。

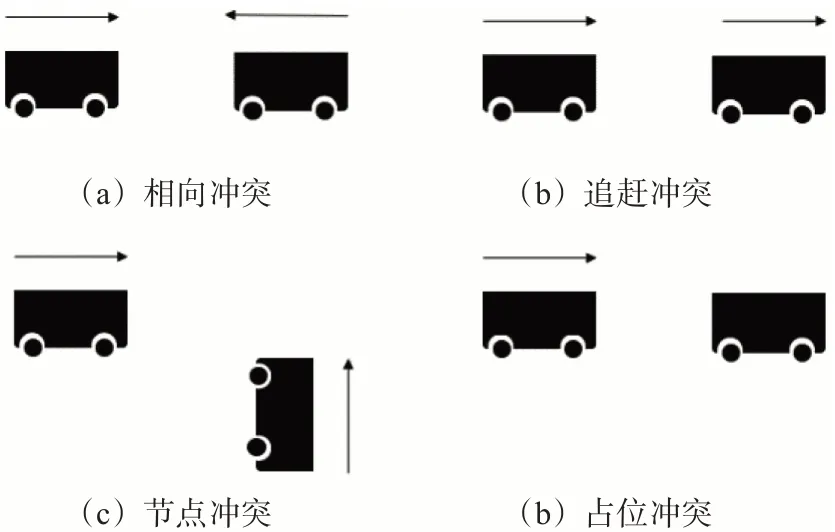
图6 AGV冲突类型Fig.6 AGV conflict type

时空网络可以在实时检测AGV 位置信息和冲突路段的基础上规避冲突。一般情况下本文的度模型迭代求解1次就可以得到多AGV间路径无冲突的调度方案。但是，当任务分配不合理时，会出现路径规划无可行解的情况：在某一时间段路网的某一区域有多台作业AGV，这个可以被称为“拥堵”现象，映射在时空网络上就是不存在起点到终点的无冲突路径。传统冲突处理策略在调整完路径后没有考虑后续影响，在这种“拥堵”情况下，冲突节点的前1个节点等待或重新调整路径可能会使得AGV 发生2 次冲突，更无法解决多辆AGV在同一节点存在冲突的问题。

自动化码头装卸作业集中在海陆两侧，因此该区域易发生拥堵现象。为了解决拥堵问题，提出了基于时空网络和自动化码头布局特点的规避方式。图7为基于时空网络的路径规划示意图，需要规划A在t时刻经过n个时间段到达C的路径。若在时空网络中不存在At到Ct+n的通路（路径中的边和节点被其他AGV遍历），此时AGV需在到达Ct+n前在等待节点进行等待wt避免拥堵，此时AGV 到达的时间网络的节点不再是Ct+n而是Ct+n+wt。

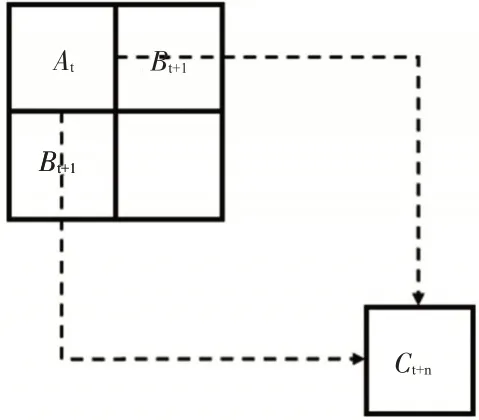
图7 基于时空网络的路径规划Fig.7 Path planning based on spatiotemporal network

针对不同的冲突类型，AGV规避冲突需要等待的时间不同。表3为不同冲突类型的等待时间计算方法。其中优先级与电量相关，电量越低优先级越高。

表3 不同冲突类型解决方法Tab.3 Different conflict types resolution methods

3.2 任务分配和路径规划算法设计

第一阶段的任务分配模型会得到多个AGV 执行任务的序列以及到达任务节点和离开任务节点的时间。将其输入路径规划模型，任务节点的坐标x，y加上时刻T为路径规划模型中构建的时空网络寻路的起点或者终点，路径规划模型基于起点和终点为AGV 作业规划无碰撞的安全路径。如果部分AGV 无法在时空网络上找到起点到目标节点的通路，则需要进行拥堵情况冲突规避和任务分配调整。时空网络的优点可以实时检测冲突并进行规避，若仍旧存在冲突，本质原因在于任务分配不均衡使得AGV 集中作业。因此需要针对冲突规避的结果将AGV 从作业点i到任务点j的等待作业时间wt加上原来执行任务的时间tijk计算出新的任务执行时间tijk+wt。在此基础上形成新的代价矩阵再次输入任务分配模型，不断迭代，直到生成无冲突的路径的AGV任务分配。算法流程见图8。

图8 算法流程图Fig.8 Algorithm flowchart

4 算例分析

4.1 小规模算例

为了说明算法流程，基于码头作业特点随机生成的小规模算例。算例由Python 随机生成，整个算法由Python 3.7 的工具包GUROBI 求解器求解。实验平台在2.20 GHz PC，16 GB RAM，Windows10，64 位操作系统上运行。如表4 所示，最早开始时间和最迟完成时间组成任务时间窗，Pi以及Di分别为该任务相关的装载或者交付任务。根据AGV 作业特点和地图设定AGV 速度为1 m/s，1 次可托运1个40FEU或者2个20TEU，需求中用40和20代表集装箱类型。以上为12个任务的小规模和5×5的小地图，因为地图较小，不另设等待节点，所有节点均可等待。

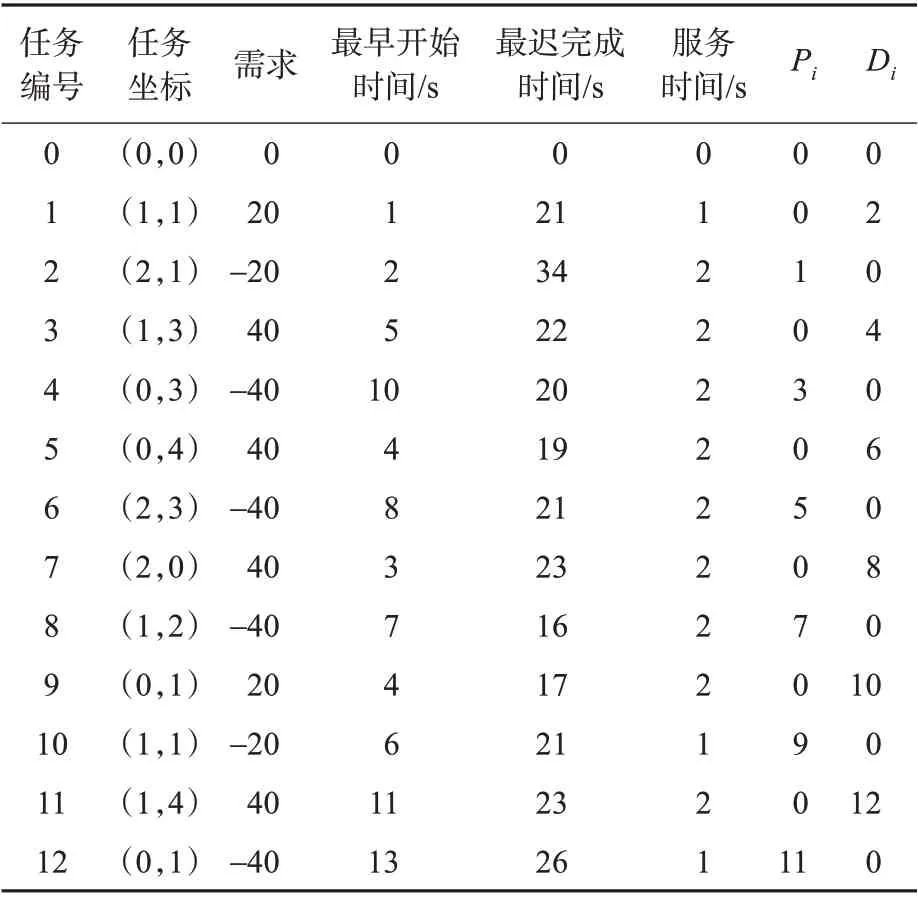
表4 小规模算例Tab.4 Small-scale study

使用GUROBI 求解两阶段的混合整数规划模型，得到AGV的作业顺序和作业路径。路径由x坐标，y坐标和时刻T表示。模型的第1 次迭代结果见表5。

由表5可见：AGV3规划路径时出现了无可行解的情况。冲突见图9，7 s时AGV3在（2，1）节点执行任务后不存在到达下1 个任务节点（1，3）节点的通路。2 个方向的道路（2，3，9）和（1，2，9）均被AGV1和AGV2遍历。

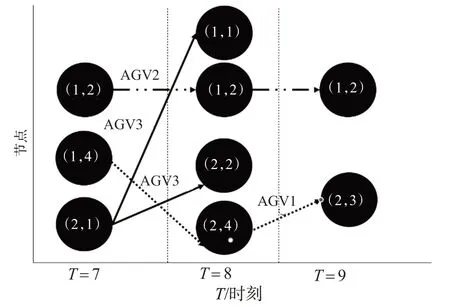
图9 冲突示意图Fig.9 Conflict diagram

表5 第1 次迭代结果Tab.5 Results of the first iteration

此时需要规避冲突，规避流程见图10，AGV在（2，1）节点等待后时空网络的目标节点更改为（3，3，11）。

图10 冲突规避示意图Fig.10 ConflictAvoidance Diagram

调整后执行任务2后执行任务3的代价已变化，再次进行任务分配得到新的任务分配和路径规划方案见表6。

表6 AGV 调度结果Tab.6 AGV scheduling results

4.2 大规模算例

为了验证模型在大规模问题下的求解速度表现和后续实验对比。基于洋山港的布局设计AGV 的实验环境。整个算法由Python 编程求解实现，其中时空网络由Python 的工具包NetworkX 编译构建。路网基于洋山港岸桥，桥吊缓冲区等关键节点建立，设立等待区域供AGV 停留以规避冲突。路网参数设置见表7。

表7 路网参数Tab.7 Road network parameters

将本文提出的求解算法（FSA-TSN）与求解PDPTW常用的遗传算法（GA）及求解器GUROBI的求解时间进行对比。根据上述路网参数随机生成20组10，20，30，40，100个任务的算例，使用上述3种算法求解，不同任务规模下3 种算法平均求解时间见表8。可见小规模任务下，求解速度是相近的。但随着任务规模的提升，求解器的求解速度不断降低，当求解任务规模达到100时，求解时间超过1 h，因此无法适应码头繁忙作业情况。与常见的启发式算法GA相比，笔者提出的两阶段算法避免了无效的插入加速了算法收敛，提高了求解速度。综上，本文的算法在求解速度上优于求解器和传统的启发式算法。

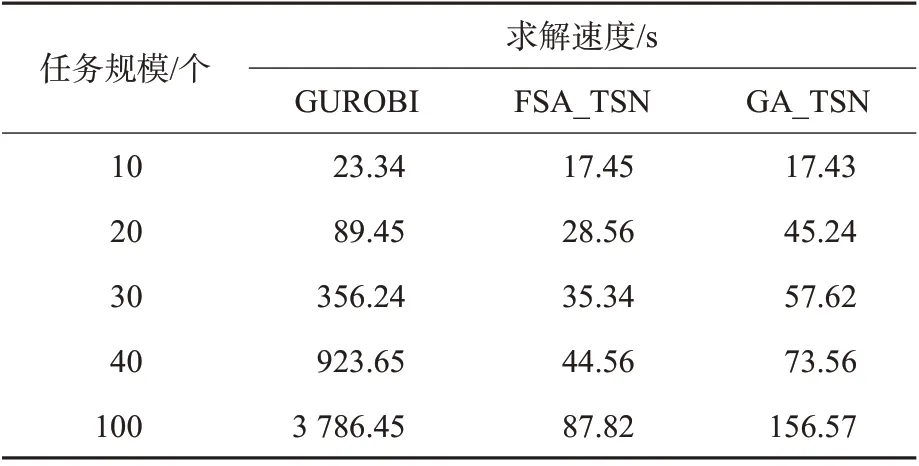
表8 不同算法求解速度对比Tab. 8 The speed comparison of different algorithms

4.3 实验设置

实验1。不考虑多AGV间路径冲突的调度模型默认任务分配后以最短路径执行任务（TAP-SP）。对比不同任务规模下本文的调度模型（TAP-TSN）和TAP-SP的冲突数量和成本。

实验2。针对拥堵情况，本文模型的调整方式是冲突规避后调整AGV 任务分配，追求AGV 路径无冲突的前提下最小化作业成本。对比本文的AGV调度模型与传统的三阶段AGV调度模型，即任务分配后基于二维路网规划路径，并根据路径规划中的冲突类型解决冲突的三阶段调度模型[13]。用任务延期时间和冲突数量及路网拥堵率3个指标来衡量算法的优劣。其中拥堵率的计算方式时总任务延误时间比上总任务完成时间[22]。

4.4 实验结果分析

实验1 结果与分析。分别用TAP-TSN 和TAP-SP求解不同规模的算例，得到冲突数量与作业成本见表9。其中，规避前的TAP-SP 作业成本是不考虑冲突前提下以最小化AGV 作业总时间为目标计算得出的，其结果存在大量冲突，且跟随任务数的增长不断增加。而实际的时间成本在规避冲突后平均增加了9.91%。与之相比，本文的算法在任务数到达600时仍旧不会出现冲突。同时该算法的成本与未考虑冲突规避的成本是相近的，最大成本增加不超过2.6%。综上，对于自动化码头AGV的调度需要完成任务分配和路径规划2方面的调度。

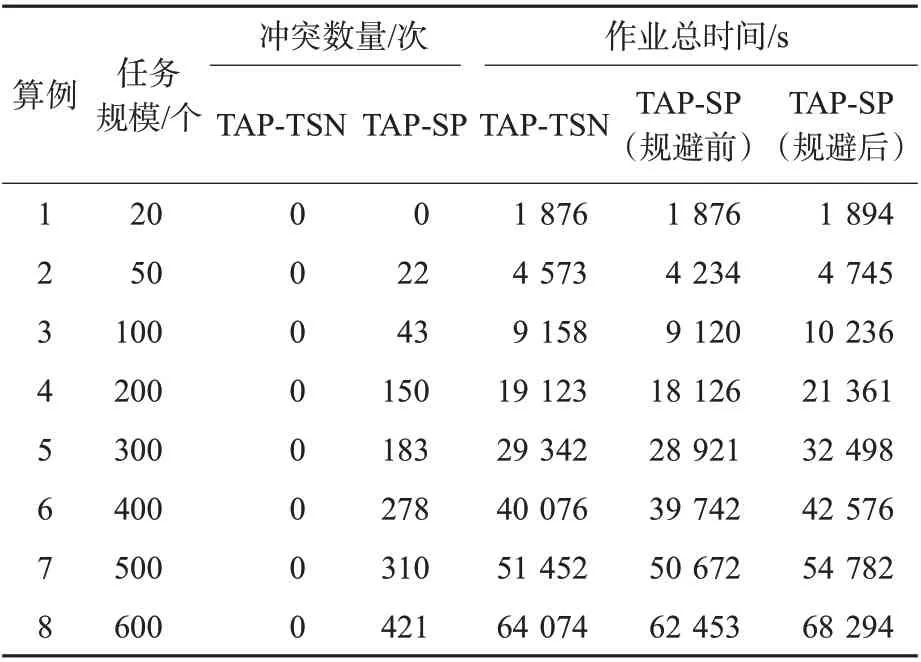
表9 TAP-TSN 和TAP-SP 冲突数量对比Tab.9 Comparison of the number of conflicts between TAP-TSN and TAP-SP

实验2结果与分析。分别用本文调度模型和三阶段调度模型求解不同规模的算例，得到任务延期时间和数量及路网拥堵度见表10。由表10可见：本文的算法可以有效地避免多AGV 间的路径冲突和任务延期。在算例中，不同任务规模下，本文提出的算法AGV路径冲突均为0，而传统避障策略在更改路径或等待后仍存在冲突。任务延期方面，本文的算法最大降低任务延期时间2 895 s。同时该算法相较三阶段的调度模型而言，降低了路网拥堵度，在任务箱数量为100，200，300，400个时分别降低5.73%，5.48%，8.47%，10.79%。因此本文提出的调度模型和冲突处理策略对于解决自动化码头AGV调度更为有效。

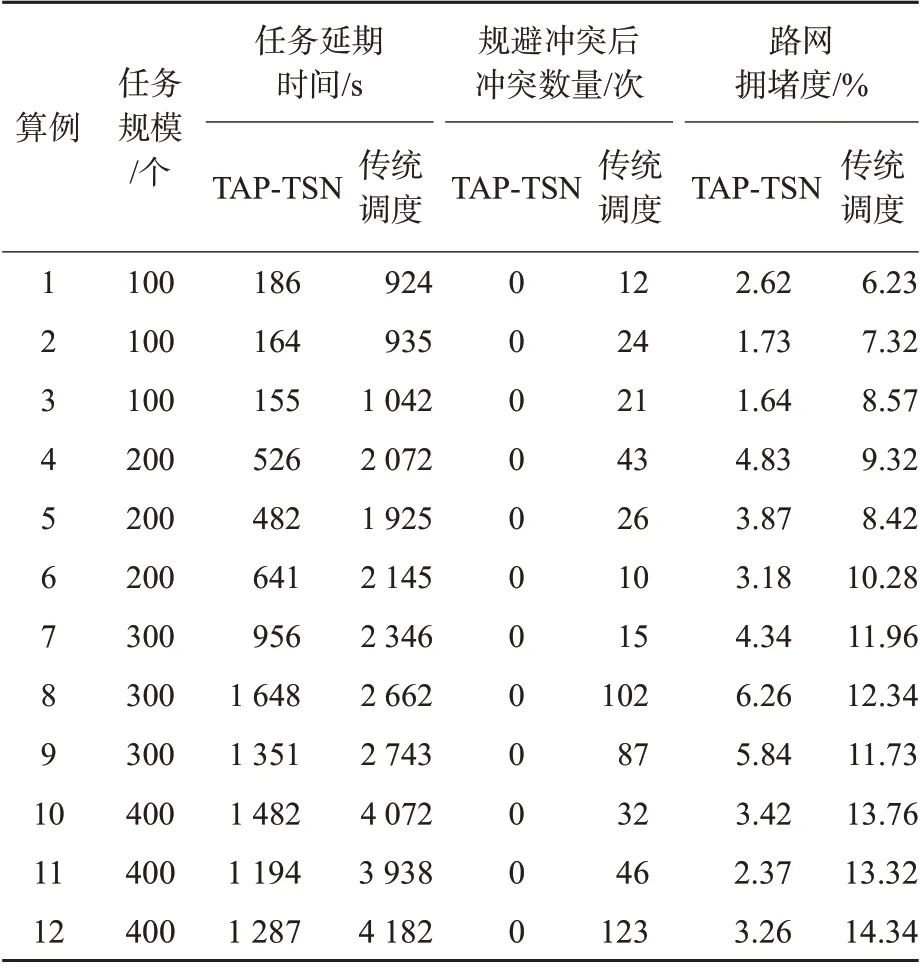
表10 三阶段调度模型与本文模型对比Tab.10 Comparison between three-stage scheduling model and this model

5 结束语

本文针对AGV调度的2个子问题任务序列分配和路径规划提出了1 个两阶段的模型，结合自动化集装箱码头布局和作业特点，构建两阶段模型解决调度中的任务分配和路径规划问题，为AGV决定任务序列分配的同时规划执行任务的无冲突路径。任务分配模型以最小化作业成本为目标，路径规划模型以多AGV间路径无冲突为目标；采用改进的模拟退火算法确定AGV作业序列，在减少任务延期的前提下，利用时空网络在规避冲突基础上规划AGV路径。针对路径规划无可行解的拥堵情况，规避冲突后重新计算代价矩阵再次进行任务分配以调整AGV 任务分配不合理带来的集中作业问题。在此基础上，与其他调度模型对比，可以得出以下结论。

1）本文综合考虑了AGV电量，多载和自动化码头的布局构建模型，符合自动化码头AGV的实际作业过程，具有较强的实用性。

2）与本文的模型对比，在不考虑冲突规避的调度模型的实验结果中冲突数量随任务规模增大不断增大，最大达到310个，因此针对自动化码头AGV调度的研究需要考虑冲突规避问题。

3）本文针对拥堵情况采取冲突规避后调整不合理任务分配的方式，避免了任务分配不均衡带来的路径冲突问题，从结果上看与不调整相比降低了任务延期时间和路网拥堵度。

本文的研究符合自动化码头AGV 实际作业过程，并在传统调度模型的基础上考虑了冲突规避问题，但还存在一些不足，两阶段模型需要多次迭代，利用启发式算法求解会有不稳定的问题，因此采用列生成算法求解本文的模型将作为未来的研究方向。