基于VMD-MD-Clustering方法的航班延误等级分类*

王兴隆 许晏丰 纪君柔

（1.中国民航大学空中交通管理学院 天津 300300；2.中国东方航空股份有限公司 上海 200135）

0 引 言

随着我国民航业的不断发展，航班数量和客货吞吐量逐年递增[1]，可用的空域资源日渐不足，航班延误数量也日益增多。对航班延误做出合理评价是分析航班延误总体水平、降低延误成本，以及制定相关处置预案的重要基础，有着重要的现实运用价值。

近年来，国内外学者对航班延误有关问题进行了深入研究。在国外，Henriques 等[2]提出了空中交通网络延误过程的新变量，并在此基础上对空中交通延误模式进行了预测。Suvojit 等[3]采集6 个维度的延误属性有关数据，通过构建增强决策树模型来分析航班延误。Yi等[4]采用多元线性回归的方法对进场航班的延误情况进行了研究。Bin等[5]通过深度学习有关方法对航班延误产生原因进行分析，并建立了延误预测模型。Miticic 等[6]将混合密度网络和随机森林回归2种概率预测算法应用于欧洲机场的航班延误预测，较好地估计了到达和起飞航班延误的等级，平均绝对误差小15 min。Shi 等[7]在提取飞行操作的关键因素后，采用机器学习的方法，提出了1种新的航班延误预测模型。

国内方面，曹悦琪等[8]考虑到航班数量的实时性，给出了基于Logistic模型的延误航班数量与航班累计延误时间的预测方法，对航班延误的后续发展做出准确的预测，从而减少损失。黄俊生等[9]对航班延误、飞机置换和航班取消3 种类型的航班延误和恢复过程建模分析，得出乘客导向的航班延误预测。王语桐等[10]提出1 种支持向量回归和多元线性回归相结合的方法建立组合预测模型。丁建立等[11]提出1种基于轻量级梯度效应的多目标航班延误预测模型，该模型结合了航班信息和气象信息，提高了对航班延误的预测准确度。姜雨等[12]提出通过时空图卷积神经网络实现对离港航班延误状况的预测。刘继新等[13]采用KNN 算法建模，在结合了以往航班运行数据和气象数据，预测了机场内短期航班延误情况。朱代武等[14]采用深度置信网络支持向量机回归方法来挖掘航班延误的内在模式，使其能在预测延误的同时进行管理措施，从而减少整体延误。

综上所述，对于航班延误问题的研究存在以下不足：①将航班延误视作相同样本，并将样本数据直接作为所构建模型的输入端，仅使用数值属性指标对所有航班延误问题作出评价；②分析航班延误只考虑数值属性指标去评估延误等级，尚未形成科学的延误等级分类规则，无法直观有效的判断航班延误程度。因此，在已有的研究基础上，综合考虑数值属性及类属性数据构建延误指标，提出1 种基于变分模态分解（variational mode decomposition，VMD）、马氏深度（Mahalanobis depth，MD）函数和数据聚类（K-means clustering）的VMC-MD-clustering方法（以下简称为V-M-C方法），研究大样本下的机场终端区航班延误情况，并以某大型枢纽机场的航班延误数据进行实例验证，本文所提方法有较好效果。

1 航班延误等级分类模型

1.1 航班延误指标选择

从时间、空间和效率3个维度，选择航班延误时间、航班飞行时间、延误影响人数和航程4个数值属性以及是否过站经停、执机机型2 个类属性指标对航班延误等级进行评价。共6个航班延误评价指标的具体说明及其影响介绍，见表1。

1.2 航班延误等级分类方法

本文选取包含类属性及数值属性在内的6个指标衡量航班延误情况，但是因为各国对于航班延误的规定并不一致，航班延误也是1 种发展变化的概念，所以航班延误数据具有数据量巨大、特征复杂、具有高维特征等特点[15]。本文提出的V-M-C航班延误等级分类方法的整体流程见图1。

图1中的具体步骤如下。

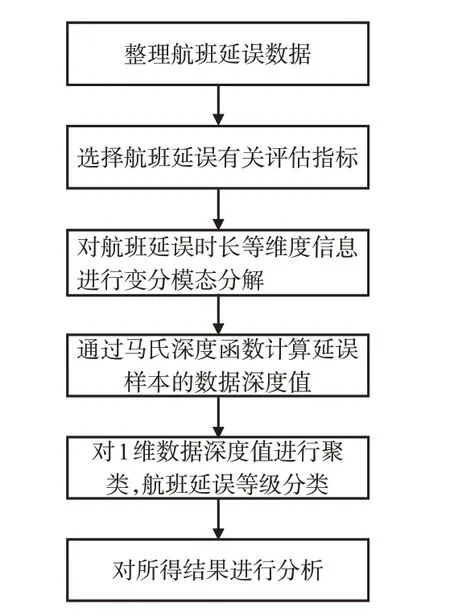
图1 航班延误等级分类流程图Fig.1 Flow chart of flight delay classification

步骤1。收集数据并整理，对某大型机场枢纽的实际运行数据进行分析，提取其中航班延误数据。

步骤2。选择延误有关评估指标，本文综合考虑机场、航空公司、管制等运行需求提出6个航班延误有关指标见表1。

表1 航班延误等级评价指标Tab.1 Evaluation index of flight delay level

步骤3。选取延误航班数据中的航班延误时长，采用变分模态分解方法去除延误时长维度中的噪声因子，减少由于过长延误时间对总体分布带来的影响。

步骤4。对延误数据进行归一化处理，通过深度函数计算样本中每组延误数据对于总体的离心程度，采用马氏深度函数对样本数据进行计算得到数据深度值。

步骤5。对一维数据深度值进行聚类处理，确定聚类系数K，判断航班延误等级。

步骤6。对得到的航班延误等级分类结果进行准确度评估分析。

2 V-M-C算法设计

聚类分析是1种无监督的学习[16]，该方法在大规模的数据集分类时，具有一定的优势。其中由于K-means 有着简单易用，对一维数据有较好的处理效果等特点，因此本文将通过K-means 算法对航班延误等级进行聚类分类。但是该算法存在着如：K值不好选取；最终结果容易陷入局部最优；对方差不同的隐含类别聚类效果不佳；对非平稳数据难收敛等缺点。故选择在K-means算法之前先通过变分模态分解VMD和马氏深度MD来对数据进行处理，从而实现K-means算法更加快速准确的进行聚类。

VMD 是1 种自适应的时频信号分析方法[17]，对非平稳信号有着较好的处理效果。通过对数据使用VMD 方法进行分解，获得相对稳定的数据集，便于后续使用K-means算法进行聚类。

MD 是建立在马氏距离基础上的1 种数据深度函数，其复杂度不随数据维数的增大而增大[18]。故本文选取MD 来处理较为复杂的航班延误数据，在降低数据处理难度的同时进一步提高了数据稳定性，提高了K-means算法的运行效率，有利于探索最优解。

2.1 变分模态分解

利用VMD分解信号，计算分解后所有本征模态函数（intrinsic mode function，IMF）的总和，在IMF重构信号总和等于给定输入信号条件下，分解出m个IMF函数um(t)，并使得到的IMF的估计带宽之和最小。

对于每个um(t)，对其进行希尔伯特变换得到其单边频率谱，见式（1）。

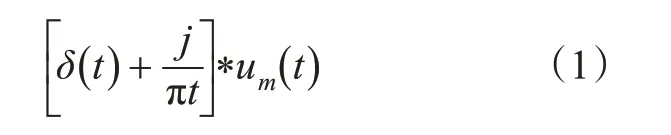
由傅里叶变换性质，将式（1）得到的频谱转移至对应基带，见式（2）。

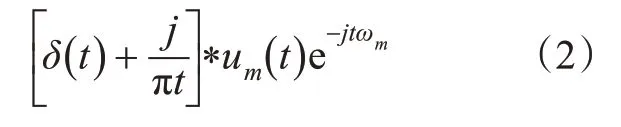
通过高斯平滑解调信号计算带宽，求解式（2）的梯度平方范数[19]，约束变分模型的表达式，见式（3）。

采用拉格朗日乘子法将式（3）中的约束问题转化为非约束的变分问题，见式（4）。

2.2 数据深度

式中：μS为航班延误数据集的均值向量；σS为航班延误数据集的协方差矩阵。

MD(S;q)值越趋近于1 时，航班f距总体S越近；MD(S;q)越趋近于0，航班f距总体S中心越远。

2.3 数据聚类

2.3.1 聚类数K的确定

对聚类的有效性的评价标准分为外部和内部2种。聚类数K就是内部评价的重要指标，通常用来确定数据集的最佳聚类数。本文综合1维数据深度序列的误差平方和与轮廓系数值确定聚类数K值，来解决随机性导致的K值选取稳定性差的情况。

手肘法是1种基于误差平方和簇内误方差（error sum of squares，SSE）的K值选择算法，SSE会随着K的增加，先大幅下降，后小幅下降，形成类似手肘的下降曲线而得名手肘法。SSE的计算见式（7）。

轮廓系数法的核心指标是轮廓系数，而轮廓系数是对聚类效果优劣的1 个重要评判方式，平均轮廓系数越大，聚类效果越好。某个延误航班fdi轮廓系数定义，见式（8）。

式中：a为fdi与同类中其他延误航班的平均距离，km；b为fdi与最近类中所有延误航班的平均距离，km。

最近簇的定义，见式（9）。

式中：fdk为某个类Ck中的1个延误航班。

2.3.2 数据深度值聚类流程

数据深度值K-means聚类算法流程，见图2。

图2 K-means算法流程图Fig.2 Flow chart of K-means algorithm

步骤1。确定最佳聚类数K，随机初始化选取k个点作为聚类中心。

步骤2。将数据深度值序列分配到距离中心样本最近的类，每次分配后更新类的中心样本。

步骤3。把每个样本分类为相应的类之后，然后重新计算中心样本和原始样本间距。若1个样本比原有的核心样本更靠近新的核心样本，则将其分配到包含新中心样本的簇中。将每个中心样本分类为自己的类后，计算样本与新中心样本的间距。如果1个样本比原始中心样本更接近新中心样本，将被重新分配至新中心样本簇。

步骤4。重复步骤3 的过程，直至算法收敛，聚类结束。

2.4 支持向量机

为确定分类结果的精确性，本文在航班延误等级分类的基础上进行了延误等级检测，采用带惩罚权重的支持向量机（SVM）模型对基于V-M-C 方法的航班延误等级分类情况进行预测。

支持向量机是1种分类算法，它在处理小样本、非线性和高维模式分类问题中显示了很多独特的优点，本文选择带惩罚权重的支持向量机可以将问题转化为如下的二次规划模型，见式（10）。

式中：P为惩罚参数，P越大代表SVM对错误分类的惩罚越大；ξi为松弛变量。

采用支持向量机对航班延误等级的分类结果进行分析，不仅可以确认结果的精确性，也在一定程度上提高V-M-C模型的普适性。

3 实例验证

选取某大型枢纽机场1个月共计4 557条航班延误数据作为样本，通过所提V-M-C方法对样本中的航班延误等级分类，并在此基础上，采用带惩罚权重的支持向量机模型对航班延误等级结果分析，实验数据，见表2，其中“是否经停”项，0为未经停，1为经停。

表2 航班延误实验数据（局部）Tab.2 Flight delay experimental data（local）

3.1 航班延误等级分类

由于不同部门对延误时间的记录存在一定差异且少部分长时间延误航班对总体延误分布产生较大影响，因此导致延误时间数据存在一定的噪声，为了增加结果的准确性，将延误时间序列数据通过变分模态分解进行降噪重构。变分模态分解参数中对信号处理结果起到主要作用的参数分别是二次惩罚因子α及IMF 信号分量个数m。本文中，α取常用的默认值α=2 000[20]，m的选取兼顾信号分解的个数与重构后信号的均方误差，取m=10。延误原始信号及重构后信号见图3。由图3可见：通过变分模态分解重构延误时间序列后，较好的维持了总体延误时间分布，减少了长时间延误航班的延误时长，使延误时间数据更贴近实际研究需求。

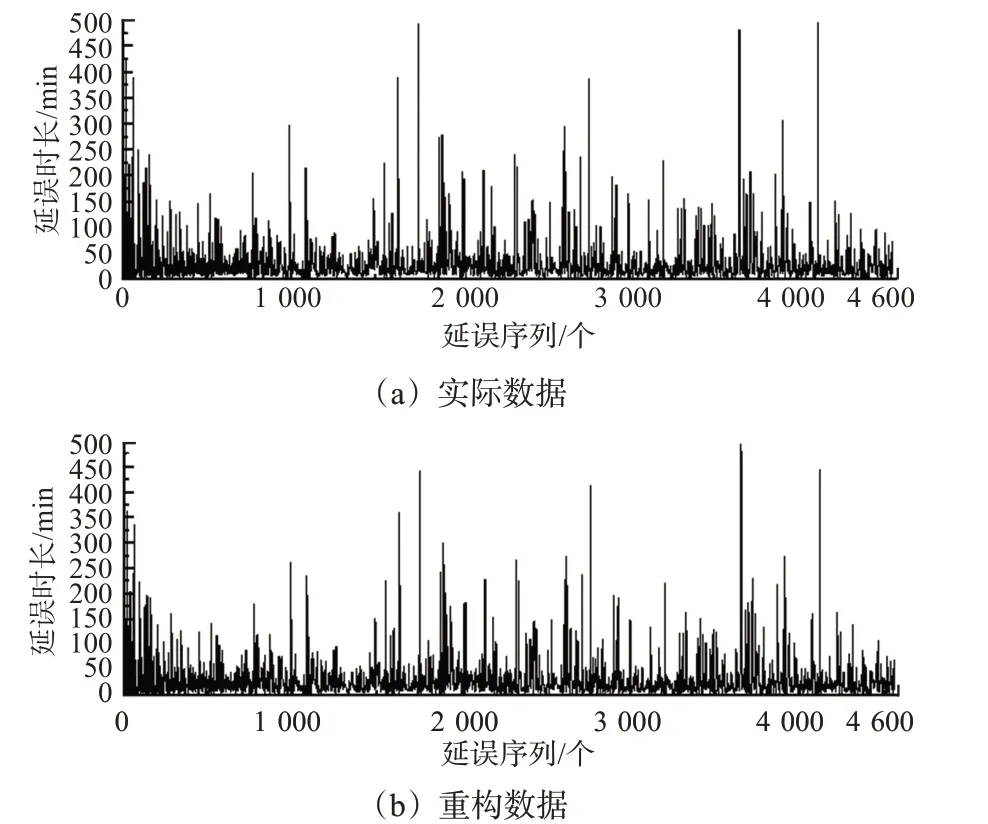
图3 延误时间序列重构对比图Fig.3 Comparison chart of delay time series reconstruction

将重构后的延误时间序列及表1中的其他维度信息作为输入，带入式（6），得到航班延误的数据深度值，航班延误的数据深度分布见图4。

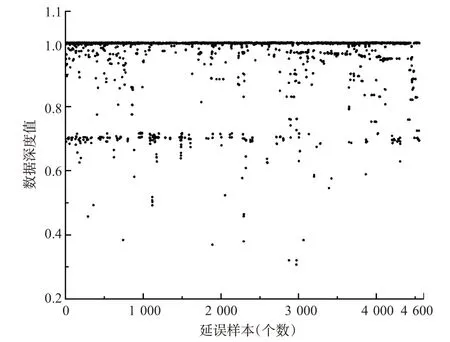
图4 延误航班数据深度值Fig.4 Flight delay data depth value

对得到的数据深度值进行聚类，划分出延误过程中的航班等级。最佳聚类数的决定方法是利用式（7）～（8）中给出的评估指标，从而对不同聚类数下样本的聚类效果加以评价。K=2～8时的误差平方和及轮廓系数变化见图5。

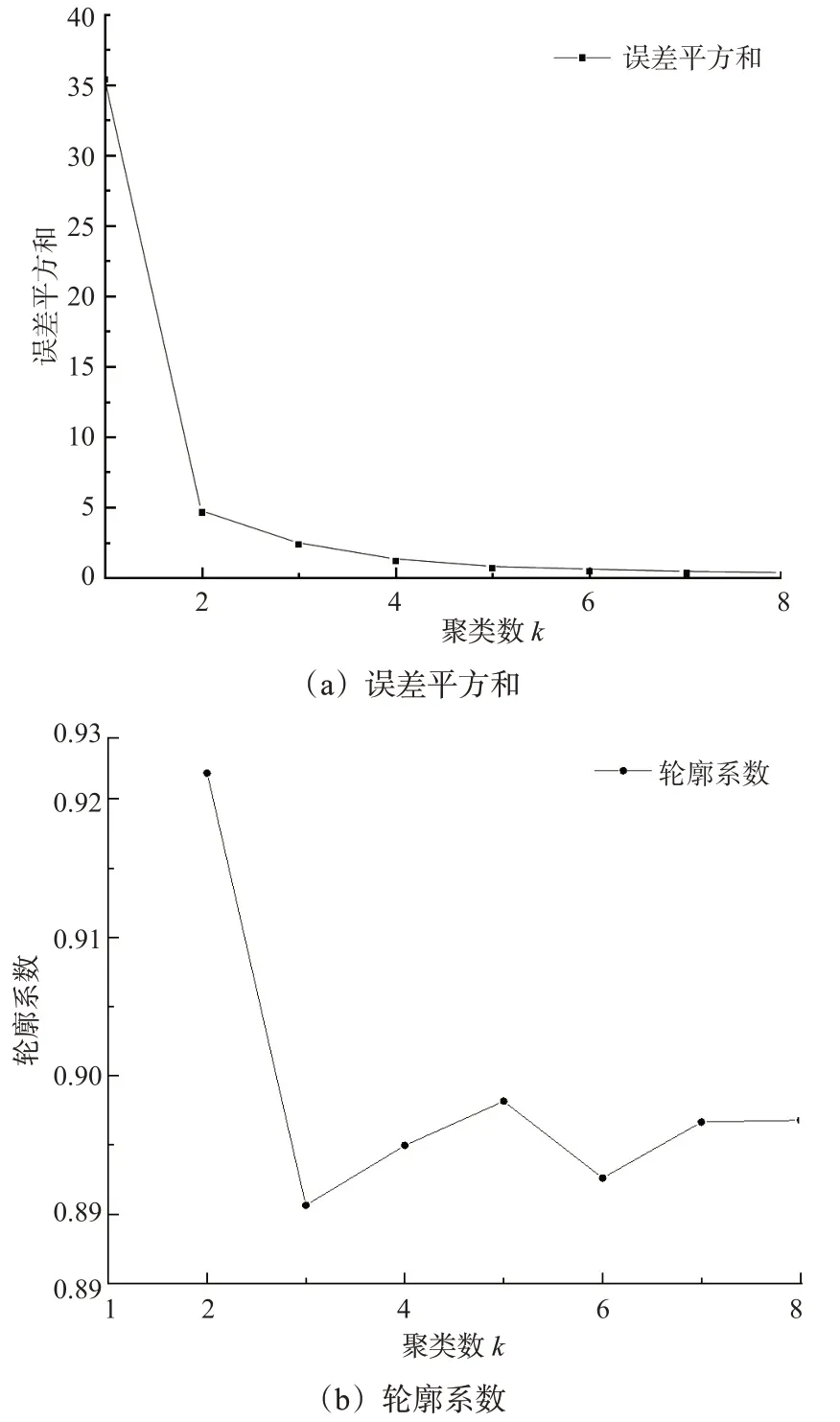
图5 聚类有关指标折线图Fig.5 Line chart of clustering related indicators

综合误差平方和与轮廓系数随聚类数的变化趋势，取k=2时聚类效果最佳。因此对航班延误的数据深度值进行聚类，即可对航班延误中的延误等级分类。

为揭示航班延误运行模式及其产生的原因，对航班延误等级的有关信息进行聚类，仍以式（7）和式（8）作为聚类数据类间分类标准，发现航班延误等级数据在k=2时聚类效果最佳，即航班延误等级可分为2个部分，记为延误等级Ι 类与延误等级Ⅱ类。

将Ι 类、Ⅱ类延误等级及其他航班延误等级信息进行统计对比，根据不同维度绘制延误雷达图，见图6。

图6 延误信息雷达图Fig.6 Radar chart of Delay information

由图6 可见：延误等级Ι 类航班主要为远程航班，该类航班多为大机型执飞，影响顾客较多的国际航线。可以看到，该类延误航班延误时长略高于其他等级的延误航班，在整体数据集中被分为Ι 类等级的主要原因是远距离航程及较高的飞行时长降低了航班延误时间维度的影响。因此在对延误航班制定有关计划时，应对远程航线进行单独考虑。

航班延误等级Ⅱ类的航班主要为有过站经停的航班，该类航班延误平均时长明显高于延误等级Ι类及其他延误等级航班，而在其他延误有关维度与其他延误数据相差不大。造成延误时长较高的原因是由于在经停过站的过程中造成由于后续航段流量控制或过站地服准备措施不完备等造成的，因此对航班延误等级Ⅱ类制定有关计划时，可适当提高延误时间容限，着重对过站保障过程进行关注。

通过对航班延误等级进行分析，发现远程航线与经停过站航班是产生航班延误等级差异的原因，且平均延误时长较长。对于被分为其他延误等级类型的航班，平均延误时间为31.55 min，平均航程为2 165.47 km，平均飞行时长为216 min，主要由为中或大型机执飞航班，平均延误影响人数为213.5人。在对延误航班进行分析时，可将其他延误等级航班各维度指标的平均值作为参考。

3.2 航班延误等级准确度评估

基于带惩罚权重的支持向量机模型对航班延误等级分类情况进行精确性评估，本文采用准确率Acc及召回率R来衡量该等级分类规则对预测精度进行判定，见式（11）～（12）。

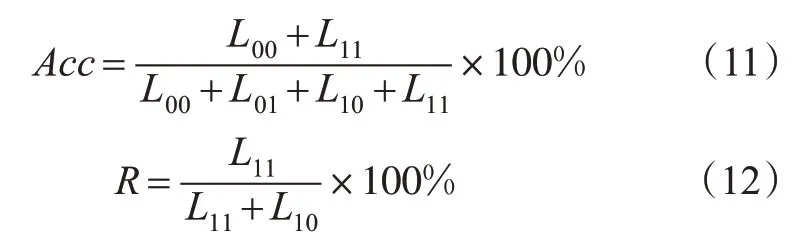
式中：L00为V-M-C 方法分类结果与预测结果均为其他延误等级航班；L01为V-M-C 方法分类结果为其他延误等级而SVM预测结果为Ι、Ⅱ类延误等级航班；L11为通过V-M-C分类方法与svm预测结果均为Ι、Ⅱ类延误等级航班；L10为分类成Ι、Ⅱ类延误等级航班，但预测结果为其他延误等级航班；Acc为从总体预测精度进行评价；R为对航班延误等级预测精度进行评价。

对数据集进行随机分类，选取其中的70%作为训练集，剩余的数据作为测试集，在rbf 核函数下，gamma=0.17，P=0.41 时模型有着较好的训练效果，此时Acc=99.56% ，R=95.41% 。由该结果可知，基于V-M-C 方法对于航班延误的分类精准度达到99.56%，对延误等级的分类精度达到95.41%。

3.3 算法对比

V-M-C方法是基于数据聚类K-means算法融合的，因此本文选择加权K-means 算法作为对比算法。对相应的评价指标设置不同的权重。结合实际情况，不同指标的权重值，见表3。

表3 评价指标权重Tab.3 Evaluation index weight

同样取聚类数K=2 时，采用加权K-means算法得出结果，并采取等级判别率对航班延误等级分类情况进行精确性评估。精确性评估公式，见式（13）。

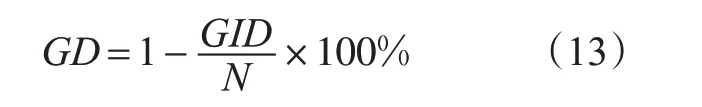
式中：N为总样本航班量；GID为分类航班延误等级与实际延误等级有差异的航班数。

对分类结果进行检验，加权K-means 的航班延误等级分类精准度只有81.9%

由以上对比实验可见，V-M-C 方法对航班延误等级分类精度比单一算法精度有较明显提升，在rbf核函数的支持向量机模型下总体判别结果稳定，能较为准确的分类航班延误等级情况。

4 结束语

针对航班延误分类问题，提出了6个指标，既包含了数值属性，也囊括了类属性。评估指标的选取较为全面，能较好的刻画出航班延误等级；同时提出基于多种方法的V-M-C 算法对航班延误等级进行分类，通过建立带惩罚权重的支持向量机模型对分类结果进行分析，实现了简单准确的航班延误等级判断。

今后可以在以下方面进行深入研究：①本文只研究单一机场的航班延误分类，后续可研究适用全国机场的分类规则；②可以进一步思考航路点、扇区的航班延误，考虑流量等指标的构建。