考虑多模式失效概率的长下坡路段重型卡车事故预测模型*

尹燕娜 温惠英

（华南理工大学土木与交通学院 广州 510641）

0 引 言

道路事故统计分析表明，长下坡路段的事故率远远高于其他常规路段，且该类型路段重型卡车事故较为常见，大多数事故较为严重甚至致命[1-2]。因此，长下坡路段的线形设计质量对重型卡车行车安全尤为重要[3-4]。现行的道路设计规范[5-6]提供了确定性的线形设计方法，规定不同设计速度下道路几何参数的最大值、最小值和一般值。但确定性方法缺乏对不确定因素（例如，车辆的行驶速度、驾驶人感知-反应时间、制动减速度等）[7-8]的定量测量，且设计道路的安全裕度是未知的。可靠性分析是量化设计道路不确定性输入和安全裕度的有效方法，在该方法中，不确定的变量被视为具有概率分布的随机变量，而非常数。

目前，可靠性分析在道路设计和事故预测中的应用研究中取得了一定成果。Sarhan 等[9]基于可靠性分析估计视距不足造成的事故风险概率。Richl等[10]通过视距不足失效概率优化事故路段道路设计参数。You 等[11]基于车辆的侧滑和侧翻失效分别建立轿车和卡车的多模式失效模型，并将其用于道路线形设计。Essa等[12]基于车辆的侧滑、侧翻、视距不足失效建立多模式失效系统，证明了多模式失效概率在平曲线设计中的应用。陈富坚等[3]基于车辆的侧滑、侧翻、制动失效提出了货车弯坡路段的可靠性设计方法。然而，文献总结发现可靠性分析用于道路安全的研究存在以下不足：①多数基于可靠性分析的道路安全研究集中于视距不足1种车辆失效模式，个别研究将可靠性分析引入车辆的侧滑和侧翻两种失效模式，鲜有文献将可靠性分析引入长下坡路段重型卡车的制动失效，将可靠性分析引入长下坡重型卡车的制动失效值得深入研究；②上述文献未见长下坡路段重型卡车的多模式失效的研究；③失效概率与车辆事故之间的关系是通过可靠性分析方法进行道路安全分析的依据，然而，很少有文献研究二者的关系。

将多模式失效概率与车辆事故建立联系，建立事故预测模型是必要的。目前，事故预测模型的研究成果较多。事故的非负性、随机性、偶发性特点使泊松或负二项模型及其衍生模型在事故预测中应用广泛[13]。然而，一些影响事故发生的因素不易被搜集，例如驾驶人生理特征、车辆使用年限、驾驶人对路况的反应等，这些因素构成未观察到的异质性因素。对未观察到异质性问题，随机效应/随机参数模型在最新的成果中常被应用。Moomen 等[14]建立随机参数负二项模型评估道路几何变量对事故频率的影响。Hou 等[15]分别建立了负二项模型、随机效应/随机参数负二项模型研究影响我国高速公路交通事故的因素，且对比发现随机效应模型与随机参数模型拟合优度相差较小。Ma 等[16]建立负二项模型和随机效应负二项模型研究道路因素对事故频率的影响，发现随机效应负二项模型拟合优于负二项模型。

上述文献的研究表明随机效应/随机参数模型优于传统的泊松/负二项模型，但随机效应泊松/负二项模型和随机参数泊松/负二项模型的拟合优度对比仍不统一，因此，将2 个模型从拟合优度、参数估计等方面进行比较分析，仍值得进一步研究。

针对现有研究的不足，笔者将可靠性分析引入长下坡路段重型卡车的制动失效，基于重型卡车在长下坡路段可能的4 种失效模式（侧滑、侧翻、视距不足、制动失效）建立多模式失效系统。以华盛顿州的长下坡路段重型卡车事故为研究对象，建立考虑多模式失效概率的重型卡车事故预测模型，挖掘重型卡车事故与多模式失效概率的关系。

1 失效功能函数的建立

可靠性分析多用于结构中，是通过数学模型将不确定因素（随机因素）与结构或系统的性能之间建立联系[17]。结构或结构的构件达到使用功能允许的某个限值的状态即为极限状态。引入极限状态方程Z（也称失效功能函数）表示极限状态，见式（1）。

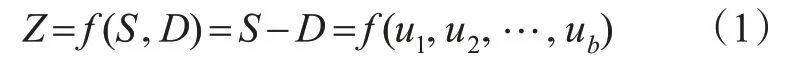
式中：S为供给函数；D为需求函数；ub为失效功能函数中的随机变量。

Z=0 表示失效面，当Z＜0 时，结构发生失效。将可靠性分析用于道路设计中，失效功能函数表示道路的供给和车辆的需求之间的差异。如果需求超过供应（即Z＜0），则认为车辆有事故风险或道路不符合设计要求。

1.1 侧滑失效功能函数

由于大部分长下坡路段包含部分弯道[3]，为更清晰表示车辆在长下坡路段行驶时的受力，本文将车辆的受力分为图1（a）的弯道受力分析和图1（b）的下坡受力分析。坐标轴方向见图1，车辆的行驶方向为x轴方向，平行于路面且与车辆行驶方向垂直的方向为y轴，垂直于路面为z轴。忽略纵向力和空气阻力，车辆受到的离心力为

式中：G为车辆的重力，N；V为车辆行驶速度，km/h；R为平曲线的半径，m；重力加速度g 为常量9.81 m/s2。

车辆在y轴方向的横向力分量为

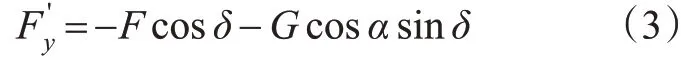
式中：α为纵坡角，（°）；δ为横坡角，（°）。

车辆在z轴方向的垂向力分量为

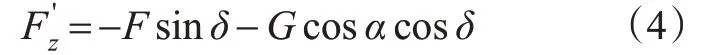
车辆在y轴方向受力平衡为

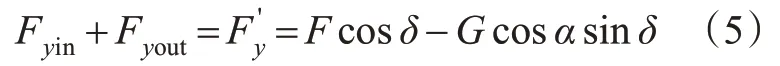
式中：Fyin和Fyout分别为内侧和外侧车轮受到的横向力，N。

车辆在z轴方向上的受力平衡为

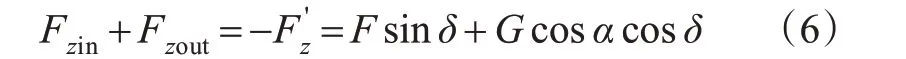
式中：Fzin和Fzout分别为内侧和外侧车轮受到的垂向力，N。

则车辆行驶所需的侧向摩擦系数μ1为

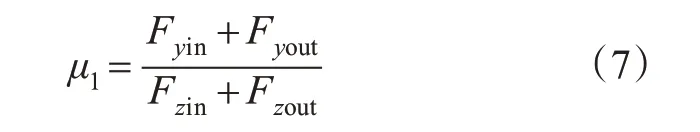
将式（5）～（6）代入式（7）。由于纵坡角α和横坡角δ通常较小，因此，sinα≈tanα≈H,cosα≈1,sinδ≈tanδ≈e,cosδ≈1。H为纵坡坡度，%；e为超高，%。则μ1简化为

与良好路面相比湿滑路面车辆更易于发生侧滑事故，因此，路面提供的附着系数μ2选择湿滑路面附着系数[18]。当μ1≥μ2时，车辆将发生侧滑，则车辆的侧滑失效功能函数Z1为

1.2 侧翻失效功能函数

由于重型卡车重心较高，在有弯道的长下坡路段行驶时，弯道内侧车轮受到的垂向载荷由于离心力的作用转移到外侧车轮，离心力越大，内侧车轮垂向载荷减小越多。当内侧车轮的垂向载荷减小为0时，车轮将离开地面，车辆即将侧翻。车辆的受力分析见图1，以弯道外侧车轮与地面的接触点为参考点的力矩平衡为

图1 车辆在弯坡路段的受力分析Fig.1 Force analysis of vehicles on combination sections of vertical and horizontal curve

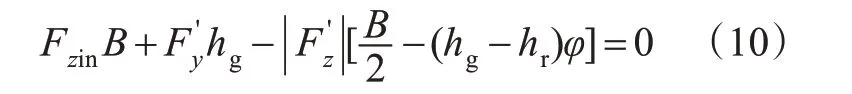
式中：φ为车辆侧倾角，φ=rφ(V2/R)；rφ为侧倾率；hg为车辆的重心高度，m；hr为侧倾中心高度，m；B为轮距，m。

将式（2）～（4）代入式（10）得

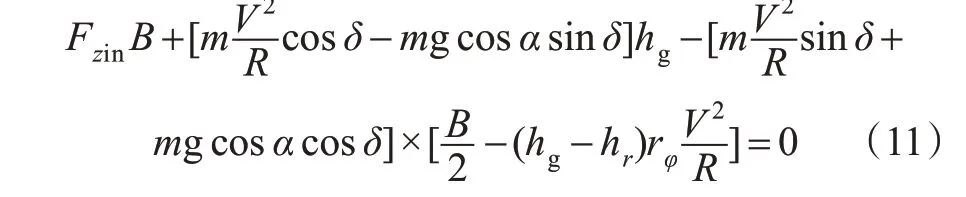
式中：m为重型卡车的质量，kg。

当弯道内侧车轮即将抬起时，则有Fzi=0，可得式（12）。

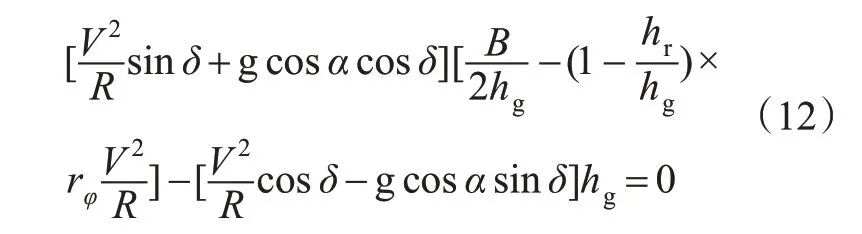
求解式（12）得到车辆不发生翻车所需要的最小半径为

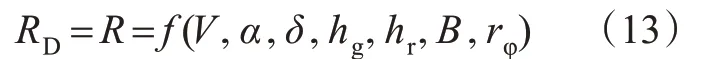
假设RS为道路所能提供的平曲线半径，则侧翻失效的功能函数Z2为

1.3 视距不足失效功能函数

停车视距是道路线形设计的主要依据，视距不足是造成交通事故的重要致因[19]。停车视距是指车辆行驶过程中，自驾驶人看到前方障碍物起，至车辆到达障碍物前安全停车所需要的最短距离[19]。当车辆在有弯道的长下坡路段上行驶时，弯道内侧的建筑物、树木、护栏等会阻碍驾驶人视线，从而导致视距不足。根据文献[6]有弯道的长下坡路段驾驶人的可用视距为

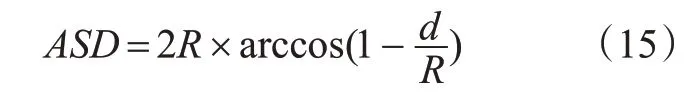
驾驶人停车所需视距为

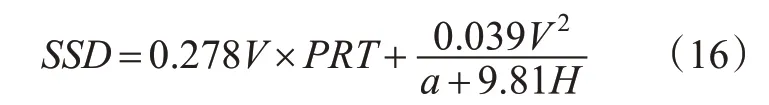
式中：ASD为可用视距，m；SSD为所需视距，m；d为横向净空，为内侧车道中心线至路边障碍物（如路边护栏）的距离，m；PRT是驾驶人感知和制动反应时间，s；a为制动减速度，m/s2。

则视距不足失效的功能函数Z3为

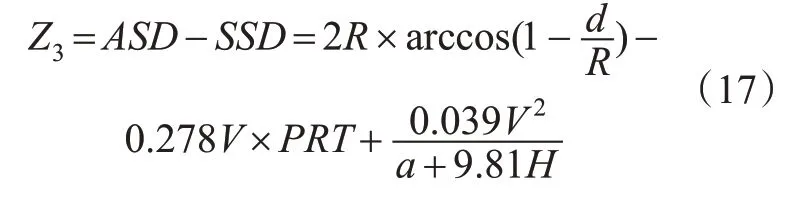
1.4 制动失效功能函数

制动器的温度是影响重型卡车连续制动性能的最重要因素。重型车辆在长下坡路段行驶时，驾驶人通常保持制动以控制车速，该操纵将导致制动器温度升高，当制动器温度超过所能承受的临界温度时，制动效能下降，从而影响行车安全[20]。因此，长下坡路段的安全设计有必要考虑重型车辆的制动失效，以提高该类型路段的行车安全性。目前，尚未有国内外普遍认可的重型车辆制动温度预测模型。本文基于文献[21]的研究成果，采用的重型卡车制动温度预测模型见式（18）～（19）。

1）当H≤0.000 215V+0.011 645。

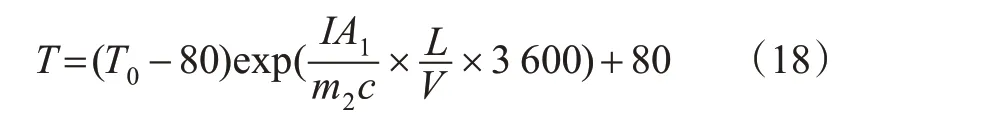
2）当H＞0.000 215V+0.011 645。

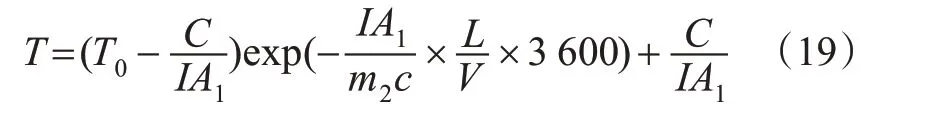
式中：C=P+80IA1；I=5.224+1.552 5Vexp(-0.0028V)；

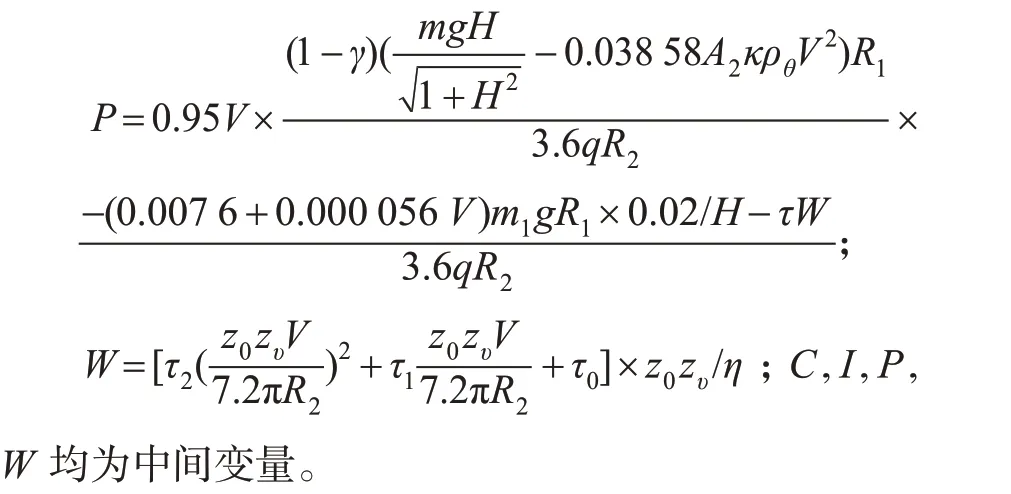
模型中变量的解释和取值见表1。

表1 固定变量及取值Tab.1 Fixed variables and values

现有的研究对重型卡车制动器的临界温度的取值不尽相同[22-23]，但基本在200～300 ℃之间。为使车辆更安全，选择相对保守的200 ℃作为制动失效的临界温度，则制动失效的功能函数Z4有以下情况。

1）当H≤0.000 215V+0.011 645。

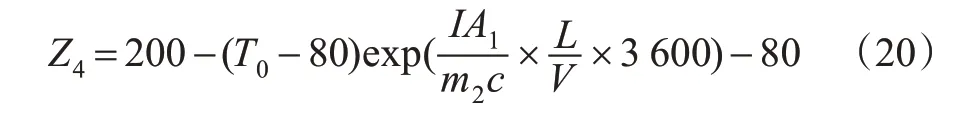
2）当H＞0.000 215V+0.011 645。

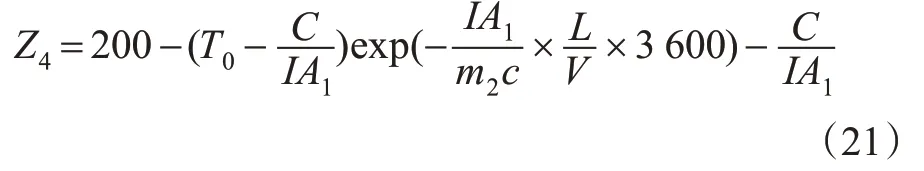
1.5 功能函数中的变量

本文将车辆运行车速、驾驶人感知-反应时间，以及制动减速度3 个变量视为随机变量，车辆设计参数、路面提供的附着系数视为固定变量，选取6×4重型卡车作为研究车型，参考文献[21]中该类型重型卡车的取值，固定变量的解释及取值见表1[19-21]。

驾驶人感知-反应时间是驾驶人发现道路前方障碍物及执行制动行为至停车所用的时间。该时间由于受道路环境的复杂程度、驾驶人的性别、年龄等的影响，并非定值。本文将该变量视为服从对数正态分布的随机变量，基于文献[7]和文献[12]的研究成果，驾驶人的感知-反应时间均值为1.5 s，标准差为0.4 s。

车辆的运行速度指在行车环境下，驾驶人基于自身条件、车辆的状况、道路情况和心理预期等而采用的安全行车速度。运行车速不仅表征道路上实际交通流的运行状况，而且受地形、公路线性、路侧景观、驾驶人的自身条件、交通组成等多重因素影响。根据文献[10]正态分布适合描述车辆在长下坡路段的运行速度分布。本文中采用的平均运行速度V85[24]和标准差模型SD[3]为

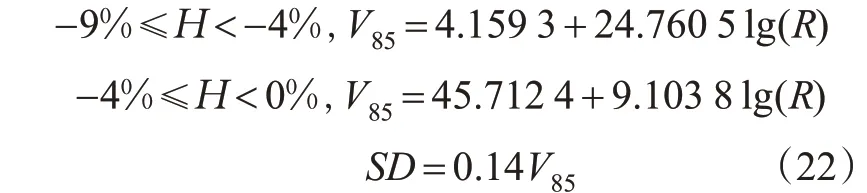
制动减速度是车辆在行使过程中迅速降低车速直至停车的能力。制动减速度是反映车辆制动效能的重要指标，受车型、车辆性能、道路的附着系数等因素的影响。基于之前的研究[12]将制动减速度视为服从均值为4.2 m/s2，标准差为0.6 m/s2的正态分布。

2 多模式失效系统的建立及概率求解

重型卡车在长下坡路段行驶过程中，上述任一失效模式出现，车辆均可能发生事故，因此，失效模式之间被视为串联系统[11，19]。根据式（1），第k个失效模式的功能函数Zk记为

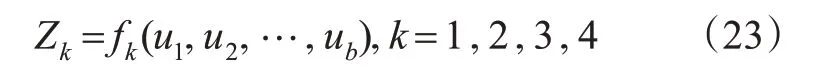
式中：k为功能函数的数量。

则第k个失效模式的失效概率为

由于失效功能函数的非线性度较高，不易求解，因此，采用蒙特卡罗方法求解单模式失效概率，蒙特卡罗方法可解决非线性程度高的问题，且比其他的模拟方法更精确和可靠[17]。

蒙特卡洛法求解失效概率须对失效功能函数Z=fk(U)的随机变量U进行随机抽样，如果Z＜0，则在模拟中道路失效1 次。若执行了N次模拟，Z＜0 出现了nf次。由大数定律中的伯努利定理可知，随机事件Z＜0 在N次独立模拟中的频率nf/N依概率收敛于该事件的概率pfk，失效概率pfk的估计值为

假设第k个失效模式发生的事件Ok表示为

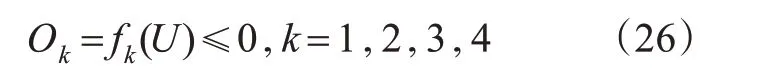
则多模式失效系统的失效事件O表示为

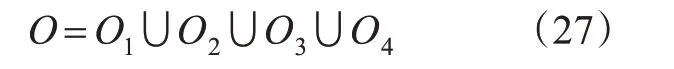
失效系统的失效概率为

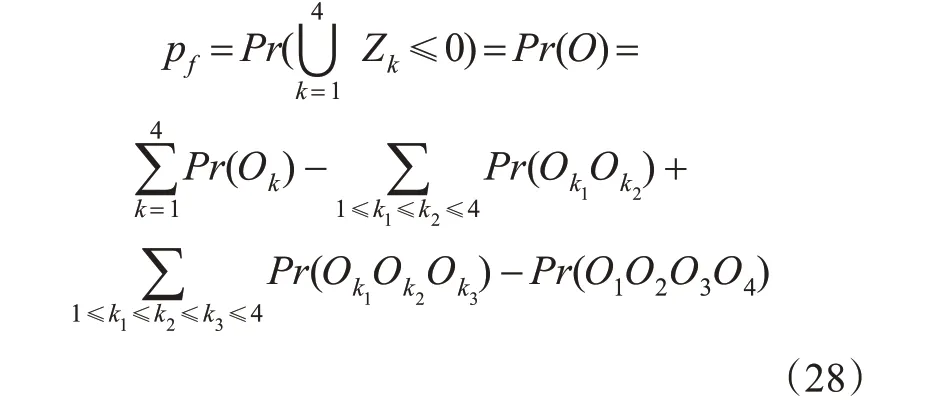
式（28）所得为多模式失效系统的精确解。但由于失效模式之间存在相关性，难以有效获得精确解，基于文献[17]本文将用宽界限法估计多模式失效系统的近似解，可有效获得系统的失效概率的估计值。

假设系统的各失效模式是正相关的，即失效事件Ok1和Ok2的相关系数相关系数＞0。意味着Pr(Ok1|Ok2)≥Pr(Ok1)，第k个失效模式的失效概率为prf=Pr(Ok)。可通过宽界限法得出系统的失效概率为

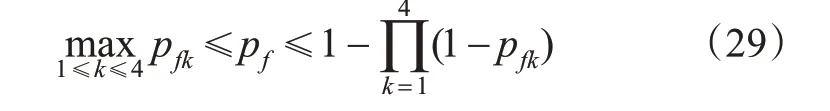
2个临界平均值作为多模式系统的失效概率，即pf为

3 事故模型构建及预测方法

将多模式失效概率作为1个解释变量与其他道路因素一并建立考虑多模失效概率的事故预测模型，挖掘多模失效概率与重型卡车事故的关系。

受长下坡路段样本量的限制，本文采用泊松模型作为基础模型而非负二项模型[25]，并建立随机效应/随机参数泊松模型用于解释不方便提供或不易被搜集的异质性因素（例如驾驶人生理特征、车辆使用年限、驾驶人对路况的反应等）。为评估所建事故预测模型的性能，采用赤池信息准则（Akaike information criterion，AIC）和麦克费登ρ2这2 个指标评估事故预测模型的拟合优度，采用平均绝对偏差（mean absolute deviation，MAD）和均方根误差（root mean square error，RMSE）估计模型的拟合精度。

3.1 模型构建

假设给定路段的事故数为Yi，泊松模型概率密度函数为

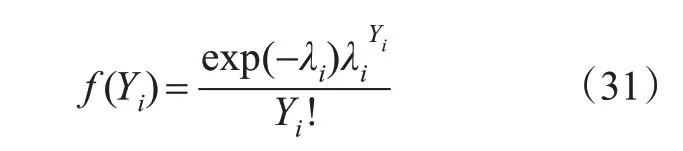
式中：λi为统计时间段内路段i事故数的数学期望，即E(Yi)=λi。泊松模型的λi可表示为

式中：β为预估参数向量；li为路段i的解释变量的向量。

为解释未观察到的异质性因素，随机参数泊松模型被采用。在该模型中解释变量的估计参数服从一定分布（如正态分布、对数正态分布、均匀分布、三角分布）[15]，随机参数泊松模型的参数为

式中：ωi为参数向量中的随机向量。

如果参数的估计标准差显著不为零，则该参数被估计为随机参数，否则估计为固定参数。随机参数泊松模型及相应的对数似然函数为

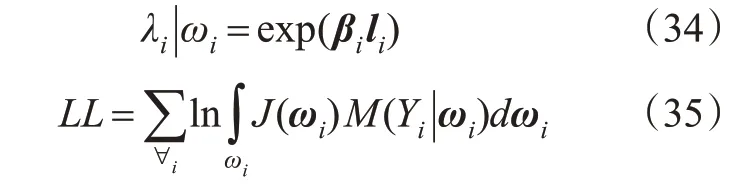
式中：J（·）为ωi的概率密度函数。

如果只有模型的截距项是随机的，则随机参数泊松模型即简化为随机效应泊松模型。由于随机参数/随机效应泊松模型的最大似然估计需要对随机变量的分布进行数值积分，计算过程相当复杂。本文使用嵌套于NLOGIT（计量经济学软件）中的最大似然估计程序[15]，基于Halton 序列对随机变量进行随机抽样，这是随机参数估计中最流行的估计技术。

3.2 模型检验

1）赤池信息准则（AIC）。赤池信息准则是估计模型拟合优度最常使用的指标，AIC越小模型拟合越好，其表达式为

式中：t为包括截距项在内的估计参数数量；LL(β)为模型收敛时的对数似然值。

2）麦克费登ρ2。麦克费登ρ2适用于随机和离散数据模型的拟合优度度量[15]，ρ2越大模型的拟合越好，ρ2统计公式为

式中：LL(0)为模型中仅含有截距项时的对数似然值。

3）平均绝对偏差。平均绝对偏差的表达式为

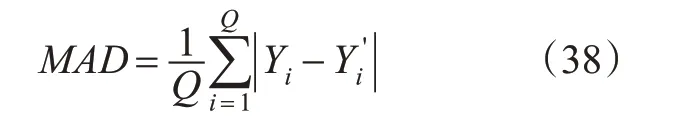
4）均方根误差。均方根误差的表达式为

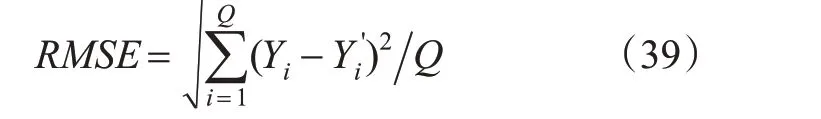
3.3 弹性分析

为研究事故预测模型中解释变量对车辆事故的影响程度，估计了模型中各解释变量的弹性[26]。弹性分析公式为

对于连续变量，解释变量的平均弹性为

式中：βj为第j个解释变量的预估参数为第j个解释变量的平均值。

4 长下坡路段事故数据描述

现有标准[5-6]和研究[27-28]尚未对长下坡路段统一定义，本文将平均坡度大于或等于3%，坡长大于或等于1 km的下坡视为长下坡路段。本研究中的事故数据和道路数据来自美国公路安全信息系统。从现有的数据库中筛选出华盛顿州71段长下坡路段，并搜集路段2006—2015 年这10 年间发生的重型卡车事故数。卡车类型基于原数据集的分类选取平板卡车、厢式货车、载重卡车和半挂车这4种卡车类型，在本文中统称为重型卡车。删除明显由于驾驶人因素（酒精、毒品、麻醉品、驾驶疲劳、疾病等）引发的车辆事故。所研究时间间隔内，筛选路段共发生645起涉及重型卡车的事故（文中称为“重型卡车事故”），包括132起单个重型卡车事故和513起涉及重型卡车的多车事故。表2为长下坡路段的重型卡车事故、道路设计参数、交通情况、路面情况和多模式事故概率的统计特征，包括最大值、最小值、平均值和标准差。

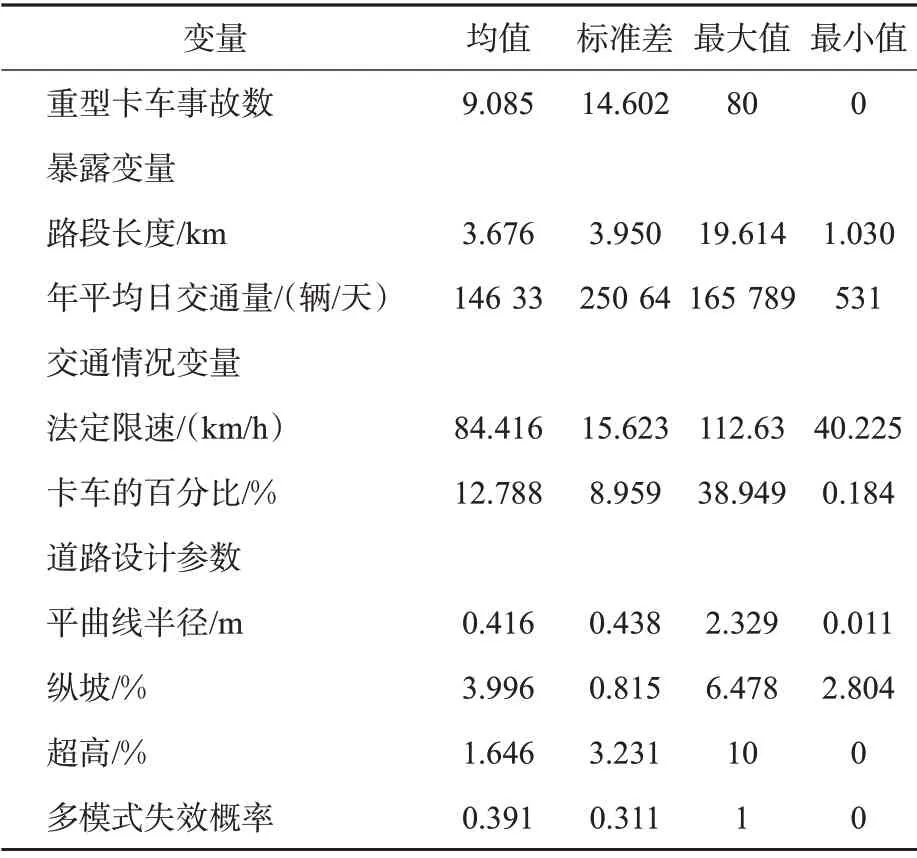
表2 变量的统计特征Tab.2 Statistical characteristics of variables

5 事故预测模型结果分析

随机效应/随机参数泊松模型中随机项测试了4种参数分布：正态分布、对数正态分布、均匀分布和三角形分布。所考虑的分布中，均匀分布提供了最佳的统计拟合。

表3为事故预测模型的估计结果。模型拟合优度指标AIC表明随机效应模型和随机参数泊松模型拟合优度相同，且二者均优于泊松模型。同理，拟合优度指标麦克费登ρ2也得到一致的结果。模型准确性指标（MAD和RSME）显示随机参数泊松模型略小于随机效应泊松模型，随机效应泊松模型小于泊松模型。综上，随机参数泊松模型略优于随机效应泊松模型，且二者的拟合均优于泊松模型。图2 为3 个模型的预测事故数与实际事故数对比图，该图表明随机效应泊松模型和随机参数泊松模型的预测事故数曲线几近重合，同时与实际事故数重合度较高，泊松模型预测值与前二者相比更离散。该结果与之前文献中对负二项模型和随机效应和随机参数负二项模型的研究结论一致[14]。因此，仅对随机参数泊松模型进行分析。

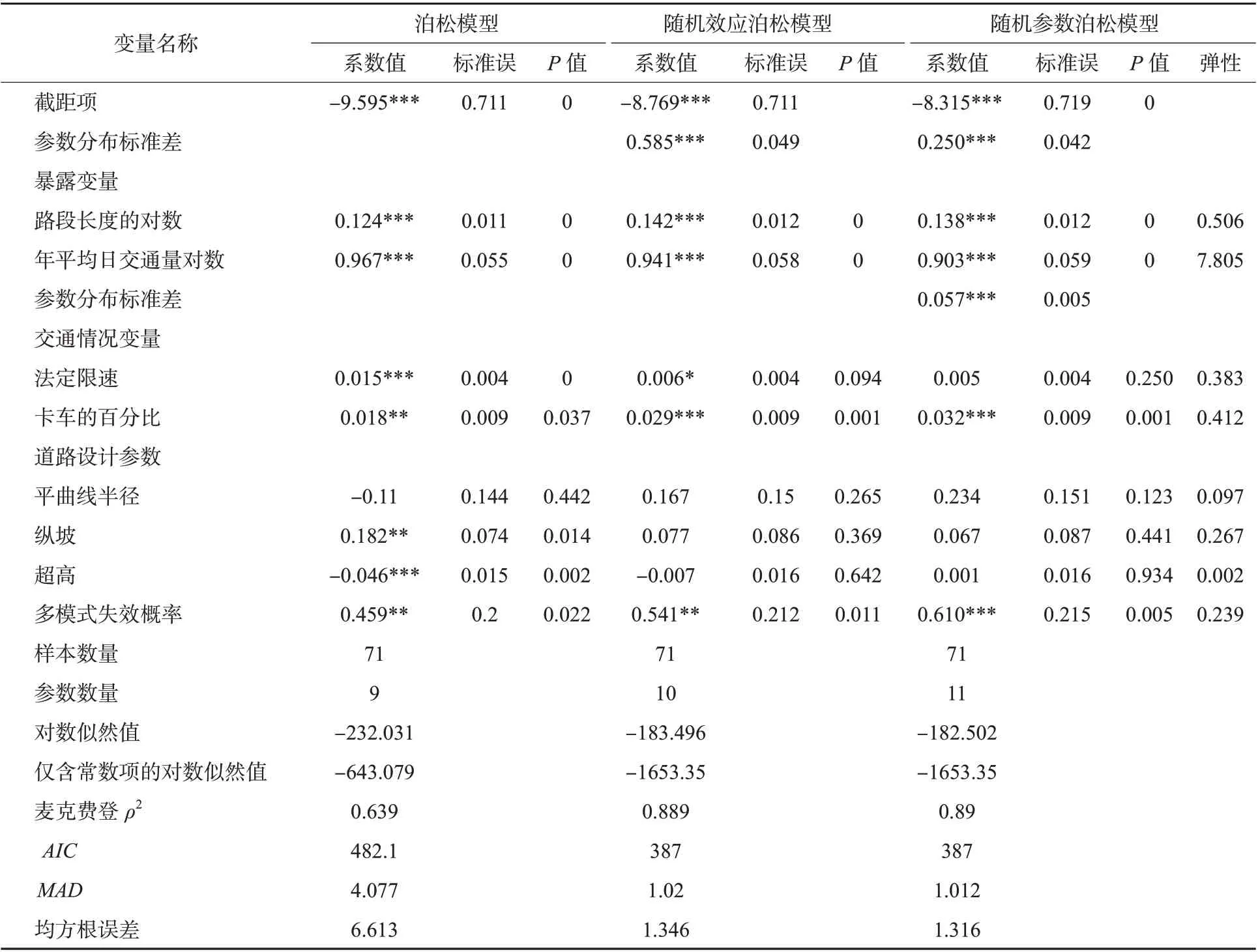
表3 考虑多模式失效概率的随机效应泊松模型估计结果Tab.3 estimation results of crash prediction model considering multi-mode failure probability

图2 预测事故数与实际事故数比较Fig.2 Comparison between predicted and actual crashes value

随机参数泊松模型仅识别出年平均日交通1个随机参数，该结果可能的原因是多模式失效系统中将部分变量视为随机变量，即部分异质性因素已被考虑。

为研究各解释变量对重型卡车事故的影响程度，随机参数泊松模型中解释变量的弹性被计算，见表3 中最后一列。弹性结果（显著变量）显示：年平均日交通（7.805）＞路段长度（0.506）＞卡车百分比（0.412）＞多模式失效概率（0.239）。与预期一致，2个暴露变量对重型卡车事故影响显著，其次是卡车百分比。在随机参数泊松模型中，解释变量的显著性表明：3个道路设计参数均不显著，尤其平曲线半径和超高，弹性分别仅为0.097和0.002，远小于多模式失效概率的弹性（0.239）。纵坡的弹性虽然较大，但显著性表明该解释变量对结果影响不显著，也不做考虑。该现象可能的解释是多模式失效系统中的功能函数包括道路设计参数，因此多模式失效概率削弱了道路设计参数对重型车辆事故的影响。

多模式失效概率的弹性为0.239，即多模式失效概率每增加10%，重型卡车事故增加2.39%。为更深入挖掘重型卡车事故与多模式失效概率的关系。令随机参数泊松模型中变量取值为表2中各解释变量的平均值，此取值下重型卡车事故数随多模式失效概率的变化如图3 中黑色虚线所示，可看出拟合曲线为Y=5.385 exp(0.391×pf)，图3 中实线为线形拟合结果，拟合的决定系数为0.997，即重型卡车事故数随多模式失效概率近似线性增加。另外，发现拟合曲线的截距不为0（5.385），即当失效概率为0 时，卡车的事故数不为0。该截距为长下坡路段的道路情况（年平均日交通、路段长度、道路限速等因素及因素之间的交互作用的影响）的影响。

图3 重型卡车事故数与多模式失效概率的关系Fig.3 Relationship between heavy truck crash values and multi-mode failure probability

6 结束语

1）本文建立了长下坡路段重型卡车多模式失效系统；提取华盛顿州71段长下坡路段重型卡车事故，建立了考虑多模式失效概率的事故预测模型，并挖掘重型卡车事故与多模式失效概率的关系。

2）模型的比较表明随机效应/随机参数泊松模型优于泊松模型，随机效应泊松模型和随机参数泊松模型拟合效果相差较小。

3）本文中研究的多模式失效概率削弱了道路平纵横对重型卡车事故的影响。

4）重型卡车事故数与多模式失效概率拟合近似直线，且截距不为0。

本文中长下坡路段重型卡车事故数与多模式失效概率之间的关系可用于辅助道路设计。若将其将其用于事故预测，还需更多的道路事故数据支撑深入研究多模式失效概率与事故数关系，可作为进一步的研究方向。该结论为可靠性分析在道路设计中进一步应用提供了依据。