山区高速公路隧道路段与开放路段的事故影响因素分析*

张 璇 唐进君 黄合来 常方蓉 王 杰 袁双林

（1.中南大学交通运输工程学院 长沙 410075；2.中南大学资源与安全学院 长沙 410083；3.长沙理工大学交通运输工程学院 长沙 410014；4.衡阳市高速交通警察支队 湖南衡阳 421001）

0 引 言

高速公路隧道具有改善道路线形、缩短通行时间、保护生态环境等众多优势。但隧道因其特殊的工程构造和复杂的通行环境，往往是事故多发段[1]。一方面，与开放路段相比，隧道路段因其内部空间半封闭、缺少自然光及行车环境单调的特性，导致隧道区域的行车驾驶难度大，容易给驾驶人带来心理上的焦虑与恐慌[2]，另一方面，隧道内外限速差别与光线明暗变化差异大，易诱发驾驶人视觉障碍[3]。此外，由于隧道内部空间受限，事故发生时灾害扩大速度快、联络与逃生困难、救援可达性差、发生二次事故几率高[4]。

近年来我国隧道交通事故尤其是重大事故频发，且多发生于高速公路，据公安部交通管理局统计资料[5]，2012—2016 年，我国高速公路隧道交通伤害事故数量增加了25%，从2012 年的244 起事故增加到2016 年的305 起，但相关事故死亡人数增加了76%，从106人增至187人。国内外学者对隧道交通事故特征及影响因素进行了研究，Ma 等[6]采用神经网络、Logit 回归模型，建立了高速公路隧道事故的伤害严重程度模型以明晰公路隧道交通事故严重程度影响因素；Caliendo等[7]构建了考虑不同伤害严重程度的隧道事故频次预测模型，分析隧道长度、年平均日交通流量、卡车比例、数等对隧道事故发生频次的影响；杨理波等[8]利用3Ds Max 软件搭建仿真模型定量分析隧道内不同照度条件下，不同组合信息对汽车驾驶人视错觉的影响；Meng 等[9]采用负二项回归模型建立了隧道追尾事故预车道测模型；Huang等[10]以道路线形、天气、时间等为解释变量，采用决策树方法构建了山区高速公路隧道群路段事故伤害严重模型来识别导致严重事故的高危情境；Hou等[11]采用随机参数模型，建立了隧道事故频次与隧道年平均交通量、隧道设计参数、路面条件的关系模型；考虑到隧道不同区段驾驶环境存在差异，部分学者对比分析隧道不同区段的事故发生频次、事故伤害严重性、事故碰撞类型等，主要结论见表1。

表1 涉及隧道分段及事故特征的文献Tab.1 Studies on zone division and crash characteristics of tunnels

国内外学者主要围绕“人-车-路-环境”4个维度对高速公路事故进行探究。基于国内3条高速公路事故，王磊等[16]采用有序Logit模型和多项式Logit模型探究事故严重程度的关键影响因素，结果表明道路线形、路面通行条件、事故时间和能见度与交通事故严重程度均显著相关；孟云伟等[17]利用二项Logistic 回归模型分析双向4 车道高速公路的事故数据，结果表明车辆类型、事故时间、路段类型、事故类型对交通事故的严重程度有显著性影响；Zeng 等[18]构建贝叶斯空间广义有序Logit 模型对中国开阳高速公路的事故数据进行分析，研究发现驾驶人类型、季节、交通量及构成、应急医疗响应时间、事故类型对事故严重程度的影响显著；AI-Ghamdi[19]采用二项Logistic回归模型对事故进行抽样分析，结果表明事故发生地点和事故形态对事故严重程度影响显著；Milton 等[20]对美国华盛顿高速公路事故采用混合Logit 模型进行分析，结果表明道路情况、环境因素以及驾驶人行为对事故发生有显著影响。

上述研究分别对隧道路段和开放路段事故发生频次及事故严重程度进行研究，但并未深入探讨隧道路段与开放路段在道路平纵线形、环境条件、车辆与驾驶人特征等因素方面的事故特征差异。基于典型山区隧道群高速公路的交通事故及道路线形数据，笔者构建了隧道路段与开放路段的事故发生倾向性模型与伤害严重程度模型，分别量化分析道路平纵线形、环境条件、车辆特征、事故原因与驾驶人特征等因素在隧道路段与开放路段的影响差异性，为山区隧道密集高速公路的安全管理对策制定提供参考依据。

1 数据准备

研究路段为沪昆高速公路邵怀段（K1341+000—K1402+000），途径区域地形险要，集中了12座隧道，属于隧道密集山区高速公路路段。从公安交通管理部门获取了该路段2011 年10 月—2016 年9 月间发生的1 537 起事故，每起交通事故包括的信息有：①事故伤害严重程度：仅财产损失（造成财产损失、未造成人员伤亡）、伤害事故（造成人员受伤、未造成人员死亡）与死亡事故（当场死亡、事故发生7 d内造成的死亡）；②事故发生环境特征：事故发生日期、时段及天气；③驾驶人与车辆特征：驾驶人年龄、过错方驾驶行为及车辆类型；④事故地点：事故发生里程桩号、方向特性。考虑到道路横纵线形是影响高速公路事故发生的重要因素[6-7]，本研究从湖南省高速公路管理局收集了详细的道路线形数据，其中上坡段的纵向最高坡度为4%，下坡段的坡度介于0.3%～4.85%之间，曲线半径范围为640～4 000 m，通过事故发生位置点的里程桩号，将道路平纵线形指标（坡度、曲线半径）与事故相关信息进行匹配。考虑到伤害事故（隧道路段占比2.86%，开放路段占比5.44%）和死亡事故（隧道路段占比1.02%，开放路段占比1.81%）占比相对较低，因此本研究中将伤害事故与死亡事故合并为伤亡事故。Huang 等[10]研究结果显示坡度大于2%的下坡更易造成严重伤害事故，因此将2%作为阈值将坡度划分为4 个分类变量，包括上下坡2%以上及2%以下。曲线半径作为连续数值变量保留其原始格式。车辆类型划分中，将驾驶小型客车、微型客车及摩托车归类为小型机动车，驾驶中型客车与大型客车归类为中大型客车，驾驶轻型货车、微型货车以及重型货车归类为货车。

考虑到隧道内外的设计速度分别为80，100 km/h，且驾驶人紧急状态下的反应时间为0.4～4 s，计算求得反应距离分别为88.9～111.1 m，因此隧道外部距洞口100 m 范围内的区域被认定为隧道影响区路段[6]，本研究将隧道内部与隧道影响区均归为隧道路段，见图1。隧道路段与开放路段的道路事故描述性统计见表2。

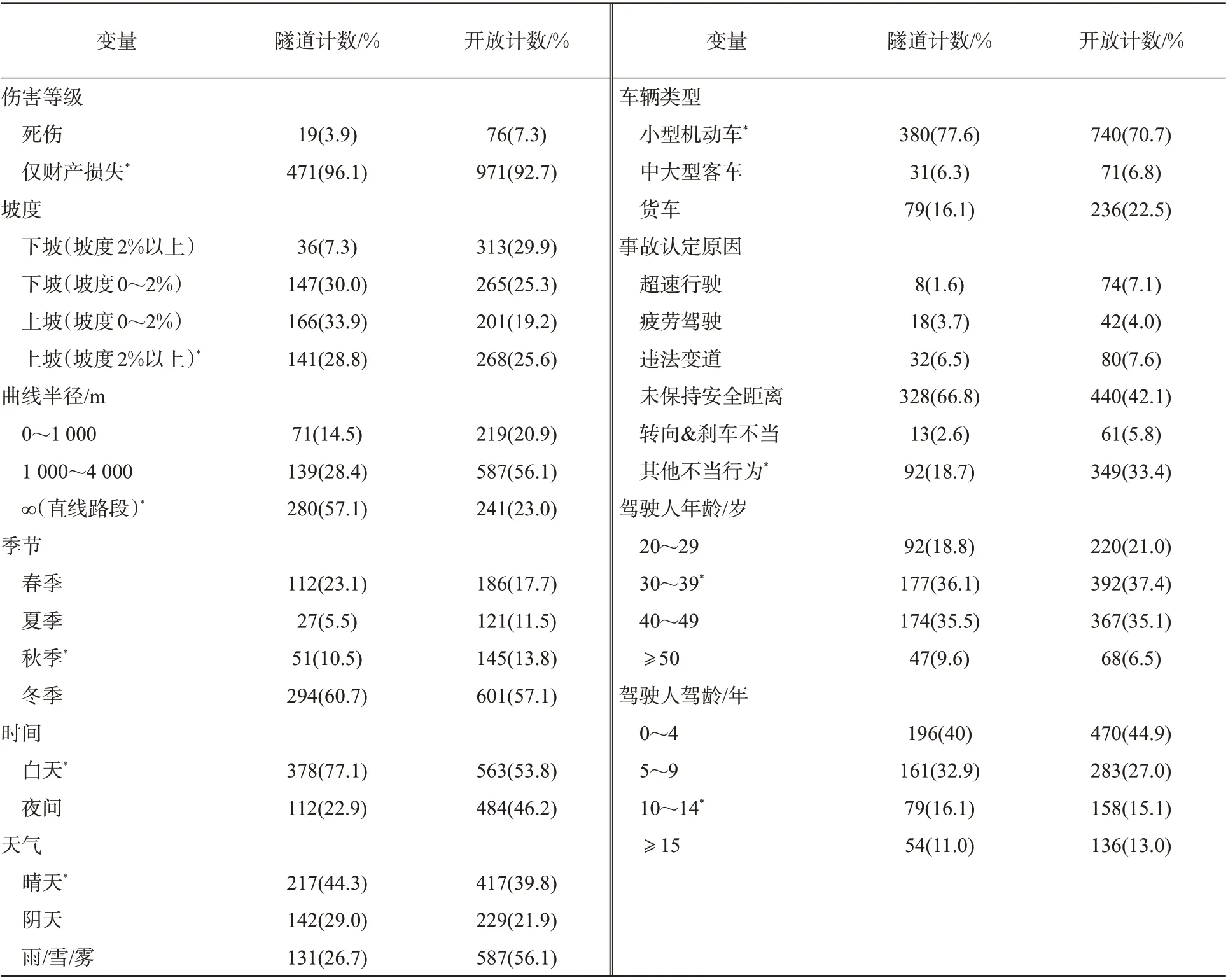
表2 变量描述性统计（若事故发生时该因素存在，赋值为1，否则赋值为0）Tab.2 Descriptive statistics of variables included in the models(1 if the variable statement is true;0 otherwise)

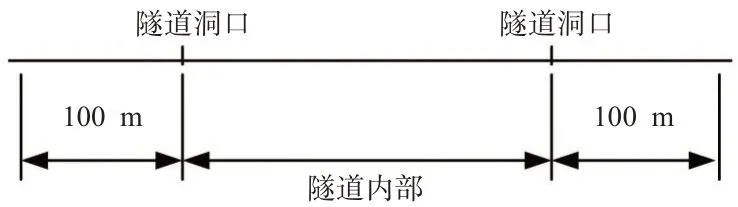
图1 隧道路段分类示意图Fig.1 Diagram of tunnel section

为判断路段类型与事故严重程度的关系，采用卡方假设检验方法。假设H0：路段类型与事故严重程度互相独立；备选假设H1：路段类型与事故严重程度相关。P值表示从总体中抽取的样本行变量与列变量时互相独立的概率，当P值小于0.05时，拒绝路段类型与事故严重程度相互独立的原假设。卡方检验的结果见表3，皮尔逊χ2值为6.581，单双侧的显著性值均小于0.05，因此拒绝原假设H0，采用备选假设H1，即认为在不同的路段，事故严重程度存在显著差异。此检验结果验证了将隧道内外路段分开进行事故严重程度分析的必有性。

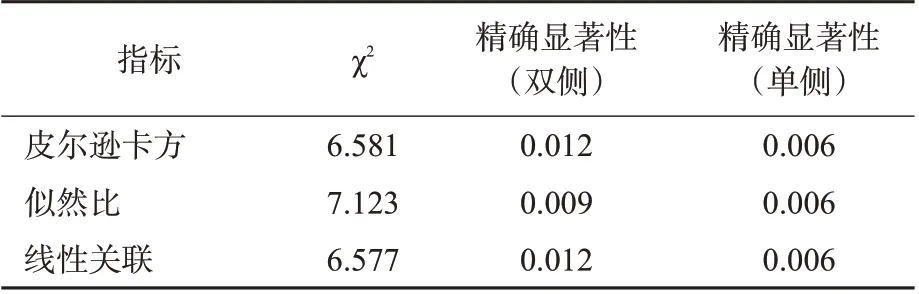
表3 路段类型*事故严重程度卡方检验结果Tab.3 Chi-square test of road section*crash severity

2 建模方法

事故倾向性的因变量为事故是否发生在隧道路段或开放路段，事故伤害严重程度的结果是否为伤亡事故，均为二分类问题。因此，采用二元回归模型用以后续分析。

2.1 二元Logit模型

建立二元Logit 回归模型分析事故的发生倾向性和2类路段的事故严重程度的影响因素。在事故倾向性分析中，y=1 代表事故发生在隧道路段，y=0 代表事故发生在开放路段；事故严重程度分析中，y=1 代表事故结果为伤亡事故，y=0 代表事故结果为仅财产损失。为得出研究问题的可估计统计学模型，隧道路段与开放路段事故发生倾向性及2类路段事故结果严重程度的效用函数为

式中：Xn为第n起事故中的解释变量向量（道路平纵线形、环境条件、车辆特征、事故特征与驾驶人特征）；β为待估计参数向量；εn为误差项。假设误差项服从极值分布，则二元Logit模型[21]的概率函数为

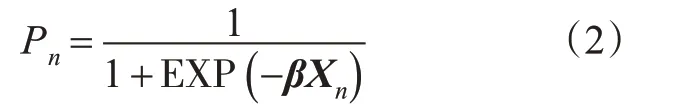
式中：Pn为事故倾向性分析模型中第n起事故发生在隧道的概率与事故伤害分析模型中事故结果为伤亡事故的概率。

2.2 随机参数Logit模型

上述模型假定各因素对事故严重程度的影响在全样本中固定不变，此假定通常与事实相违背，即β中参数估计可能因未观察到的异质性而在每起事故中的有不同的可能性。

此现象导致有偏估计和错误推断，为解决此问题，专家提出允许变量的估计参数在全样本中可变的随机参数模型[22]，其概率函数为

式中：Hn为第n起事故中的解释变量向量（道路平纵线形、环境条件、车辆特征、事故特征与驾驶人特征）；αn为解释变量的随机系数向量；γn为效用函数的误差项。

随机参数的表达式见式（4）。

式中：α为待估计参数的常数向量；ξn为误差项，该函数可反映出异质性条件对参数的影响。

事故发生在隧道路段或事故为伤亡事故的概率为

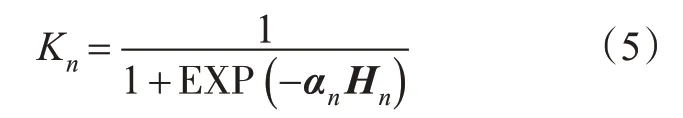
2.3 均值异质性模型

对随机参数模型并不能解释造成随机系数的可能影响因素，近期应用广泛的考虑均值（方差）异质性的随机参数模型[23]可以很好地解释数据分析中存在的异质性问题。因此，构建均值异质性的二项随机参数Logit模型用以相关分析，其效用函数为

式中：Qn为第n起事故中的解释变量向量（道路平纵线形、环境条件、车辆特征、事故特征与驾驶人特征）；λn为解释变量的随机系数向量，其函数表达式为

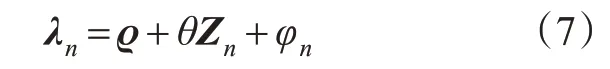
式中：ϱ为待估计参数向量；θ为解释变量的随机系数；Zn为与道路平纵线形、环境条件、车辆特征、事故与驾驶人特征等影响均值异质性的变量向量；φn为随机项，解释数据中可能存在的异质性。

事故发生在隧道路段或事故为伤亡事故的概率函数[23-25]为

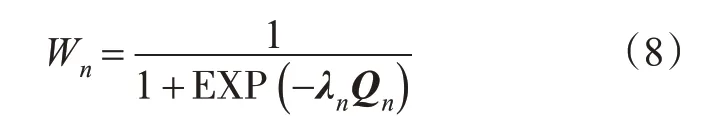
2.4 模型选择

为选择稳定性较好与预测误差较小的最佳预测模型，采用最大似然值估计法作为模型选择的依据，抽样次数取值为200次[26]。将AIC作为评价模型复杂度和衡量统计模型拟合优良性的标准，其函数表达式见式（9）。

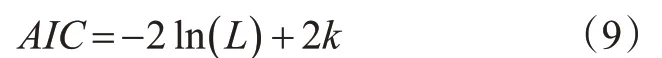
式中：L为该模型的似然函数最大值；k为所拟合模型中变量的个数。k越小表明模型越简洁，L越大表明模型越精确，因此选取AIC作为模型选择依据可兼顾简洁性与精确性。AIC值越小或者模型收敛的对数似然值越高，估计概率分布越接近真实分布。

3 结果分析

3.1 拟合优度检验

拟合优度检验结果见表4，AIC值越小或者模型收敛的对数似然值越高，估计概率分布越接近真实分布。在事故倾向性模型中，估计结果显示本文中所包含的变量均未对随机参数模型中的随机参数均值有显著影响，因此该部分无均值异质性随机参数的相关拟合优度结果。而随机参数Logit模型的AIC值为1 510.9 小于二元Logit 模型的AIC值1 534.7，故而选择随机参数Logit 模型作为事故倾向性模型。

表4 拟合优度检验表Tab.4 Goodness-of-fit measures for models

在事故严重程度模型中，2类路段均采用均值异质性模型探究与事故严重程度相关的因素。然在隧道路段模型中随机参数未表现出均值异质性，随机参数Logit 模型与二元Logit 模型的AIC 值显示2个模型的拟合优度无明显的差距（＜5），考虑到随机参数模型可揭示更多的异质性信息，因此选取随机参数模型结果分析隧道路段事故严重程度。在开放路段事故严重程度模型中，均值异质性的随机参数模型AIC值与二元Logit模型及随机参数Logit模型AIC值无显著差异（＜5）。但是，鉴于均值异质性随机参数模型可以更好地解释异质性，因此开放路段选择均值异质性模型作为事故严重程度分析依据。

3.2 事故发生倾向性

2 类路段事故发生倾向性的研究模型结果见表5，结果中显著变量包括下坡（坡度2%以上）、曲线半径（1～1 000 m）、曲线半径（＞1 000～4 000 m）、夏季、夜间、雨/雪/雾、超速行驶、疲劳驾驶、未保持安全距离。

表5 2 种路段事故发生倾向性影响因素研究模型结果Tab.5 Estimate results for crash tendency models

道路平纵线形因素中的下坡（坡度2%以上）、上坡（0～2%）、曲线半径（0～1 000 m）、曲线半径（＞1 000～4 000 m）参数估计值分别为-1.330，-1.329，-1.430，-1.341，表明与此类因素相关的事故发生在开放路段的概率更高，优势比（odds ratio，OR）用于比较2组事件发生概率的比值，根据表5中OR值可判断出该变量引发的交通事故发生隧道路段的概率分别是开放路段概率的0.264，0.265，0.239，0.262 倍。其中，上坡（坡度0～2%）、曲线半径（＞1 000～4 000 m）为随机参数，标准差分别为0.163，0.155。我国《公路隧道设计规范》[27]对洞口内外的平面线形做了相关规定，故而隧道路段在设计阶段已考虑驾驶人行车安全，这可能是与道路平纵线形因素相关的事故发生在开放路段概率更高的原因。

环境因素中，夏季、夜间、雨/雪/雾在模型中的参数估计值分别为-0.779，-0.953，-0.484，表明与此类因素相关的事故发生在开放路段的概率更高，根据优势比值判断出该变量引发的交通事故发生在隧道路段的概率分别是开放路段的0.459，0.386，0.616倍。湖南省属亚热带气候，夏季阳光强烈、气候炎热，驾驶人行驶于开放路段时更易受阳光曝晒与炎热气温影响，易产生烦躁情绪，失去耐性，这可能是增加开放路段夏季事故发生的概率的原因[10]。

事故认定原因中，超速行驶、疲劳驾驶、未保持安全距离为显著变量，其系数估计分别为-1.038，0.864，0.909，表明与超速行驶相关的交通事故发生在开放路段的概率更高，该变量OR值为0.354，表明与该因素相关的事故发生在隧道路段的概率是开放路段的0.354 倍，且超速行驶为随机参数，标准差为1.825。考虑隧道内外的设计速度分别为80，100 km/h，因此隧道路段低限速设置及洞口设警示牌的措施[28]可能是与超速行驶相关的事故在隧道路段发生概率较低的原因。与疲劳驾驶、未保持安全距离相关的事故更发生在隧道路段的概率更高，根据其OR 值可判断出与该变量相关的交通事故发生在隧道路段的概率分别是开放路段的2.375，2.482倍。与开放路段相比，隧道路段行车环境单调的特性[2]可能是导致与疲劳驾驶相关的事故发生在隧道路段概率更高的原因。

3.3 事故严重程度

表6为隧道路段与开放路段事故严重程度影响因素模型结果。表中隧道路段事故严重程度模型表明下坡（坡度2%以上）、夏季、超速行驶、未保持安全距离对隧道路段事故严重程度影响显著，其中下坡（坡度2%以上）、夏季、超速行驶参数估计值分别为1.223，1.347 4，1.445，表明这3个变量会加重事故的严重程度，且下坡（坡度2%以上）、超速行驶这2 个变量具有随机参数特性，标准差分别为0.501，0.791。OR 值表明该因素的出现相对于参照项伤害事故发生的概率增加的倍数，下坡（坡度2%以上）、夏季、超速行驶优势比分别为3.397，3.951，4.242，表明该变量影响下事故严重程度分别增加3.397，3.951，4.242 倍。陈昭明等[29]研究表明事故频次与道路纵向坡度呈正相关关系，驾驶人在陡下坡路段行驶时对车辆的控制能力降低，发生事故时不能及时采取躲避措施，会造成相对严重的交通事故[8]，本研究进一步发现与陡下坡相关的事故发生在开放路段的概率更高，但对隧道的事故严重程度影响更为显著。

表6结果表明对开放路段事故严重程度影响显著的因素包括与固定物碰撞、超速行驶、疲劳驾驶、未保持安全距离，与隧道路段事故严重程度影响因素存在显著差异。与固定物碰撞在隧道事故严重程度模型中不显著，但在开放路段模型中显著且其估计结果显著，其参数均值为-1.218，表明该因素有潜在降低开放路段事故严重程度的可能性，这一结果与赵新勇[30]的对沪蓉高速的研究中与固定物碰撞在一定程度上抑制了事故向更严重的程度发展的结论一致；超速行驶在2 类路段参数估计值均为正数且具有随机参数特性，在开放路段参数估计值为0.998，标准差为0.453，OR值为2.713，在隧道路段严重程度模型中OR 值为4.242。马壮林等[4]与Zeng等[18]的研究结果均表明，超速行驶与隧道路段及开放路段事故严重程度均显著相关，对2 类路段事故严重程度结果对比，进一步表明与超速行驶相关的事故在隧道路段严重程度更高。此外，开放路段事故严重程度模型中超速行驶的均值异质性受到“货车”这一车辆类型的影响表明与超速行驶相关的事故中，若发生事故的车辆为货车会对驾驶人起保护作用。疲劳驾驶这个变量仅在开放路段事故严重模型中显著，其参数均值为1.569，OR 值为4.802，表明该因素导致伤害事故发生的概率增加4.802 倍，其可能原因为疲劳驾驶导致驾驶人对周围行车环境认知和反应迟钝从而导致严重事故[31]。未保持安全距离在2 类路段的模型中的参数估计均为负值，在开放路段中，其参数估计值为-2.117，表明该行为相对于其他不当行为造成伤害事故的概率较低。

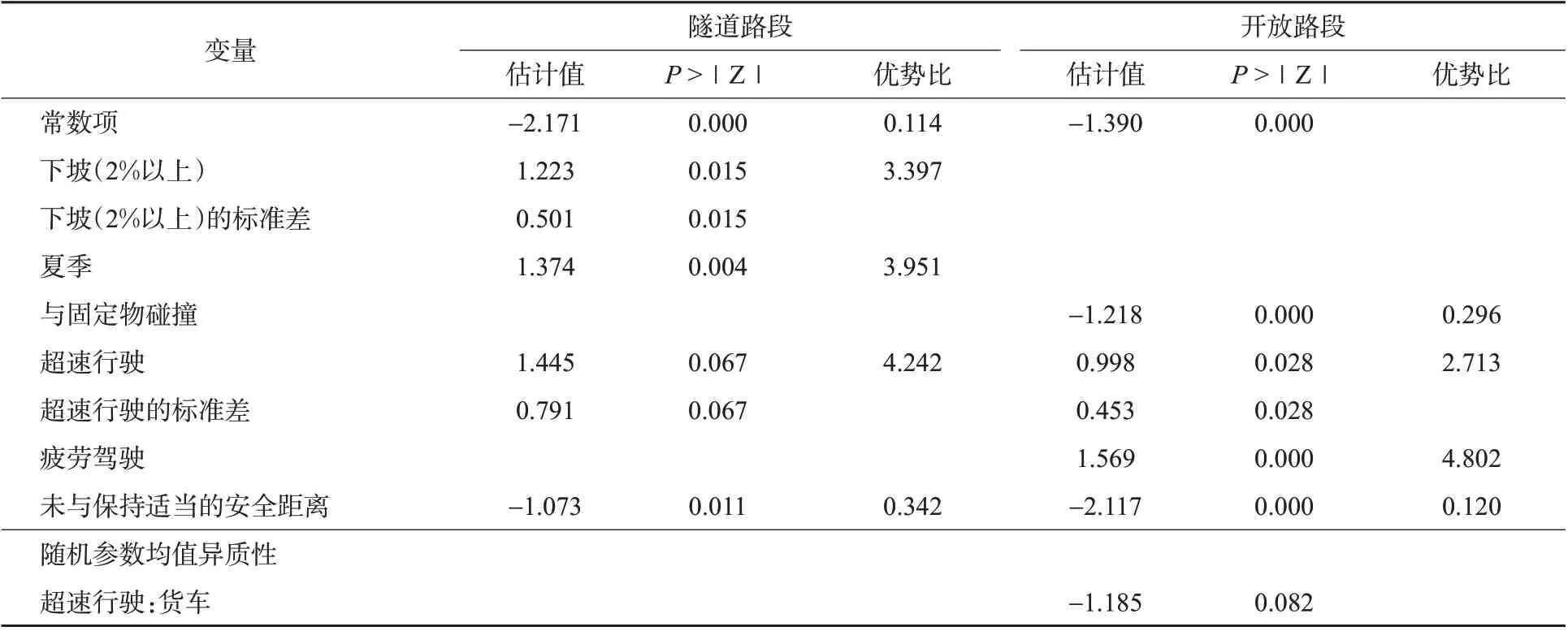
表6 隧道路段事故严重程度影响因素模型结果Tab.6 Estimate results in tunnel for crash severity models

4 讨 论

依据本文山区高速公路隧道路段与开放路段事故严重程度对比的结果，结合我国高速公路交通安全现状，从道路设计、完善隧道安全设施、加强驾驶人安全教育与管理3个方面提出战略性对策建议为我国山区高速公路交通安全问题提供可行科学决策依据。

1）道路设计。模型结果显示在陡下坡（坡度2%以上）的隧道路段交通事故严重程度增加。在陡下坡区域，如果车辆制动不及时或不当，车辆很可能失控，导致翻车事故。尤其在隧道路段环境相对封闭的条件下，驾驶人较难注意到道路线形的突然变化，在陡下坡路段行驶时难以做出及时的反应或制动措施。因此隧道路段道路设计阶段应增加对道路设计的安全风险评估，尽量避免道路环境的突变，考虑其容错、纠错能力，让驾驶人有修正错误的时间与空间。

2）完善道路安全设施。结果表明由夏季、夜间、雨/雪/雾等不利天气引发的事故倾向于发生在开放路段，因此在不利环境条件下可以采取路侧安装遮光板减少太阳直射、调节夜间照明、安装路侧警示标志提醒司机小心驾驶等措施减少交通事故的发生；而发生于夏季的事故在隧道路段造成事故严重的可能性更高，建议对高速公路隧道各区段照明安全进行科学评估[32]，通过调节隧道接近段和出口路段的灯光亮度，做好隧道内的增光和减光措施，为驾驶人提供较易适应的光线变化环境，进而减少隧道内交通事故的发生[33]。

3）驾驶人安全教育与管理。研究结果表明超速行驶会显著增加隧道与开放路段发生严重事故的概率，疲劳驾驶会增加开放路段发生严重事故的概率，该结果与Chu[31]的研究中疲劳驾驶导致驾驶人反应时间变慢、判断能力减弱、警觉性降低以及安全意识降低，最有可能与发生致命事故的结论一致。隧道作为1 种特殊的道路交通设施，对于隧道安全改善一方面需要技术设施手段的支撑，另一方面也需要驾驶人正确的驾驶行为，尤其是驾驶人对于隧道内可能存在驾驶风险的理解，因此有必要针对超速、疲劳驾驶等不当驾驶行为加强安全教育，并加大对超速和疲劳驾驶等违规行为的执法力度。

《中华人民共和国道路交通安全法实施条例》（以下简称为《道路安全法》）对全国所有高速公路道路使用者强制实行限速，小型车最高时速为120 km/h，其他机动车最高时速为100 km/h，尽管如此，超速行驶仍然是高速公路驾驶人最常见的违章行为之一，因此有必要针对超速行为加大监管力度；在疲劳驾驶方面，《道路安全法》强制性规定：“驾驶员连续驾驶4 h 后最少休息20 min”，此外2021 年1 月《道路旅客运输企业安全管理规范》规定：“驾驶员累计驾驶时间不得超过8 h，在高速公路上行驶超过600 km的车辆应配备2名以上驾驶员”。然而，疲劳驾驶行为仍是屡见不鲜。相比于中国的人均可支配收入从2004 年的6 226 元上升至2014 年的20 167元，对超速、疲劳驾驶行为的罚款却一直保持在20～200元，罚款成本较低可能是驾驶人未能遵守这些法规的原因之一[10]，因此，针对这2 种违法行为可考虑增加罚款金额与执法力度。

5 结束语

本文基于湖南省高速公路沪昆高速邵怀段2011年10月—2016年9月间发生的1 537起事故，分析了隧道路段与开放路段事故发生倾向及事故严重程度的差异性。

1）不同影响因素对隧道路段与开放路段事故发生概率的影响存在差异。与疲劳驾驶、未保持安全距离相关的事故发生在隧道路段的概率更高；与下坡（坡度2%以上）、上坡（坡度0～2%）、曲线半径（0～1 000 m）、曲线半径（＞1 000～4 000 m）、夏季、夜间、雨/雪/雾、超速行驶相关的事故发生在开放路段的概率更高。

2）影响隧道路段与开放路段事故严重程度的因素存在差异。隧道路段严重程度模型中下坡(坡度2%以上)、夏季、超速行驶与事故严重程度成正相关，未保持安全距离与事故严重程度呈负相关。开放路段事故严重程度模型中超速行驶、疲劳驾驶与事故严重程度呈正相关，与固定物碰撞、未保持安全距离与事故严重程度呈负相关。研究结果表明影响隧道路段与开放路段事故严重程度的因素存在显著差异，且同一因素对2 类路段的事故伤害结果影响存在差异。

3）研究表明2 类路段的事故伤害严重程度影响因素差异较大，建议针对山区高速公路的管理应考虑路段差异制定改善隧道路段严重事故多发的现状的相关方案。