网联环境下考虑非优先车辆延误的公交优先信号控制方法*

谭百宏 邱志军 张 祎 何书贤

（1.武汉理工大学智能交通系统研究中心 武汉 430063；2.武汉理工大学交通与物流工程学院 武汉 430063）

0 引 言

公共交通运量大、运行成本低，能有效缓解道路交通资源不足引起的出行效率问题，但其舒适度低、行程时间长，降低了乘客的乘坐意愿[1]。公交优先策略（transit bus signal priority，TSP）以城市公共交通为主导优化交通管控手段，可以减少公交出行时间，提升公交系统服务水平。

公交优先策略分为被动优先、主动优先和自适应优先[2]。被动优先和主动优先无法适应不断变化的交通环境[3]，难以协调公交车和非优先车辆的交通需求，而且存在优先请求相互冲突的矛盾[4]。自适应优先以某一指标为目标函数对交叉口信控资源进行优化，不仅为公交车提供优先权，还考虑了其他非优先车辆的通行需求，对交通系统的负面影响较小。

窦慧丽等[5]研究了单交叉口情况下基于车道的公交优先自适应控制模型。马万经等[6]研究了优先感应控制的信号切换方式。李振龙等[7]研究了通过补偿非优先相位时长以平衡交叉口需求的公交优先策略。Xu等[8]提出了以冲击波模型预估公交延误从而进行信号控制使交叉口人均延误最小化的策略。汪林[9]研究了利用预测各种配时下的公交延误的方法优化信号灯配时，更好地兼顾了非优先车辆的通行。

当道路交通流量逐渐变大，容易出现多辆公交同时发出优先请求的情况。He等[10-11]曾分别提出过1 种启发式优先算法模型和1 种混合整数线性规划模型处理这类冲突；Ye 等[12]也提出过1 个处理冲突请求的决策模型，而且还考虑了乘客在站台等候公交车时产生的延误。张鹏等[13]也针对多优先请求问题提出了1 种算法，算法以公交车车速调整量和相位时长调整量作为优化变量，建立了公交车车速引导和交叉口信号配时集成优化的线性规划模型，为减少“先到先服务”策略的不利影响提供了新的思路。

另外，部分学者还对延误预判和信控方式进行过创新，可以为策略的改进提供参考。Truong 等[14]研究了公交专用道上公交车的运行特点并建立了公交优先控制模型，综合考虑了公交车所在位置和排队对到达时间的影响建立状态方程预判延误。蔡雅苹等[15]提出过1 种基于信控和车速引导的针对连续交叉口的双层优化方法，并以福州市金山大道为背景进行了算法仿真，结果表明其策略可以大幅度缩短多条公交线路的行程时间；强添纲等[16]基于公交车运行速度和驻站时间，提出过1 种仅利用绿灯延长策略的主动优先控制方式。Jia等[17]提出过1种通过对比每1次优化前后的效益函数值决定是否更改绿灯时长的方法实施公交优先，而且专门梳理了信号机与算法之间的控制逻辑，可以作为仿真系统控灯流程的参考。

当前，智能网联技术日趋成熟，较多学者将研究方向转向了此领域。周莉等[18]曾评估过网联环境下公交优先策略的效果。柏海舰等[19]和乔文鑫等[20]曾研究过网联环境下以公交车准点性、可靠性为目标的公交优先信控策略。可见，环境感知、智能决策等新技术逐渐开始与公交优先策略相结合[21]，使得公交优先信号控制逐渐变得更加智能、精细化[22]。

当前关于网联环境公交优先策略的研究主要针对网联车渗透率较高的场景开展，而当前的网联环境并不能很好满足其对数据质量的要求。当前，社会车辆网联渗透率较低，难以利用所有车辆的轨迹数据去预判延误，而且社会车辆权重较低，利用轨迹延误预测方法会增加运算压力却不会对总体的预测精度有很好的提升作用。

笔者参考当前网联环境下的公交优先信号控制方法，根据公交车和社会车辆的权重与延误分布特点，简化了延误预测方法。通过车辆轨迹数据计算到达率，利用时距图和相结合的方法改进延误预测模型，构建兼顾公交车和社会车辆通行需求的单交叉口公交优先模型。

1 场景描述

以智能网联交叉口为对象，研究公交优先信号控制方法，其设备部署方案见图1。路口安装了智能路侧单元（roadside unit，RSU）及多接入边缘计算单元（multi-access edge computing，MEC）。当装载有智能车载单元（on-board unit，OBU）的智能网联公交车进入有效车路通信范围时，便通过V2I通信（vehicle to infrastructure）与RSU进行实时数据交互，将公交车实时位置、速度和载客数等信息转化为结构化数据传输至MEC。

图1 智能网联交叉口示意图Fig.1 Intelligent connected intersection diagram

信号机可以将当前相位配时信息（signal phase and timing data，SPaT）传输至RSU，路侧摄像头和雷达可以获取当前交叉口交通状态并转化为结构化数据传入至RSU。RSU将上述信息传输至MEC，利用以总加权延误最小为目标函数的混合整数线性规划模型计算最佳配时，并将优化后的配时信息反馈到信号机，以此实现公交优先信号控制。

传统的公交优先策略未根据公交车的特点将其与非优先车辆单独讨论，使得大量的算力投入到了权重较小的社会车辆延误计算却并未显著提升延误预测精度。

本文以车辆轨迹数据计算到达率以及交通流冲击波波速，分别利用时空轨迹图与定数延误理论推导公交车与非优先车辆延误表达式，并以加权总延误最小为目标计算出最佳的相位切换时刻，在不过多影响延误预测精度的情况下预估交通需求，减少算力浪费，更好地为交通管控手段提供参考。

2 优化过程建模

本研究选取公交车延误和非优先车辆延误构建加权延误，并将其设定为优化目标函数。

2.1 车辆到达率与冲击波波速估计

为了推导网联公交车和非优先车辆延误表达式，需要基于交叉口车辆轨迹数据求解车辆到达率及交通流冲击波波速。当前，轨迹数据的质量较差，难以直接介入延误计算，因此选用轨迹数据估计到达率间接计算延误值。

2.1.1 车辆到达率

定义相位p车辆i的到达率为，见式（1）。

本研究暂只考虑交叉口饱和度不高的情况，因此车辆出现多次停车的概率较小，且延误预测过程对到达率的预估精度要求并不高，因此参照车辆到达泊松分布特征，可得车辆到达率泊松分布概率函数，见式（2）。

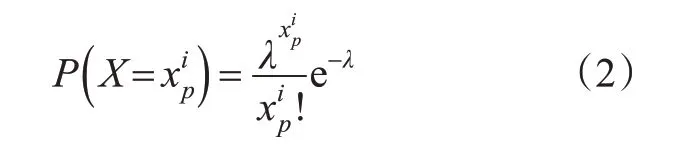
式中：λ为极大似然估计参数。

到达率极大似然估计函数见式（3）。

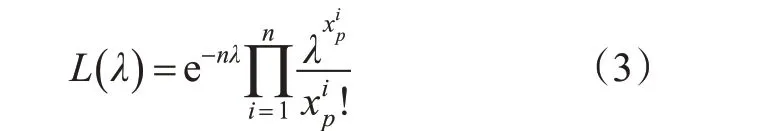
2.1.2 冲击波波速

交通流冲击波包括车辆排队形成的排队波、绿灯启亮时车辆离开交叉口形成的驶离波和绿灯启亮后排队车辆离开交叉口形成的消散波。其波速根据交通流流体力学理论[24]计算，其值为2种交通流状态流量差和密度差的比值，i和j这2种交通状态形成的冲击波波速值见式（5）。

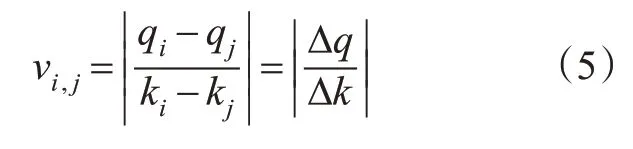
式中：qi为状态i的流量，veh/s；ki为状态i的密度，veh/m。

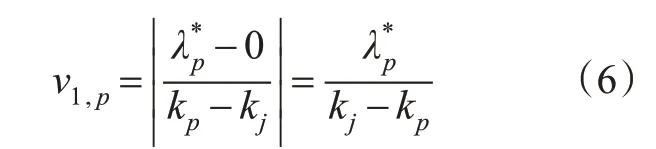
式中：kj为饱和密度，veh/m；kp为相位p对应通行方向车流的平均密度，veh/m。

当处于排队区的车辆离开路口进入驶离区时，车辆间相互作用较小，可视为以最大流量驶离，则驶离波波速v2,p见式（7）。

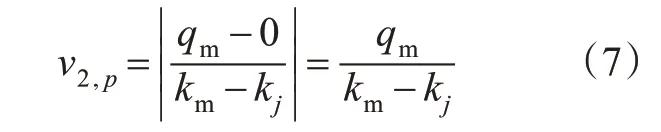
式中：qm为最大流率，veh/s；km为流率最大时的车流密度，veh/m。

当车辆逐渐驶离，排队长度减少，交通流逐渐变回自由流状态，因此消散波波速v3,p见式（8）。

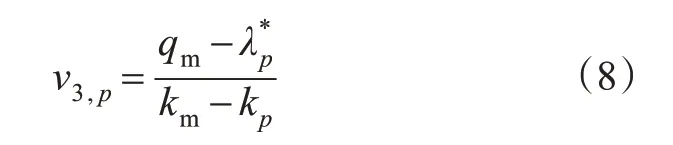
2.2 公交车延误估计

公交车作为优先车辆，其乘客数多，权重系数相对较高，因此其延误计算模型基于延误产生过程而建立。

公交车时空轨迹图见图2，黑色粗实线表示排队长度，排队增长和减少的速度分别为排队波波速v1,p和消散波波速v3,p；黑色细实线是驶离波曲线，其斜率为驶离波波速v2,p；灰色粗虚线是公交预计轨迹曲线；灰色细虚线是公交期望轨迹曲线，用于辅助推导各类延误的值；横轴为时间，纵轴表示车辆到交叉口停车线的距离。vb为公交车在自由流条件下行驶的车速；Q(p,k)为第k周期相位p的初始排队长度，tp,k、Gp,k分别表示第k周期相位p绿灯开始时刻和绿灯时长；tQ,p(p,k)是排队波与驶离波相交时刻，表示位于LQ(p,k)处的排队车辆开始消散；tQ,b(i,p)是公交车与排队波相交时刻，表示此时公交车加入排队，且到路口停车线的距离为dQ(i,p)；tv2Q(i,p)为公交车轨迹与驶离波相交时刻，表示处于排队中的公交车i此时开始启动准备离开路口。

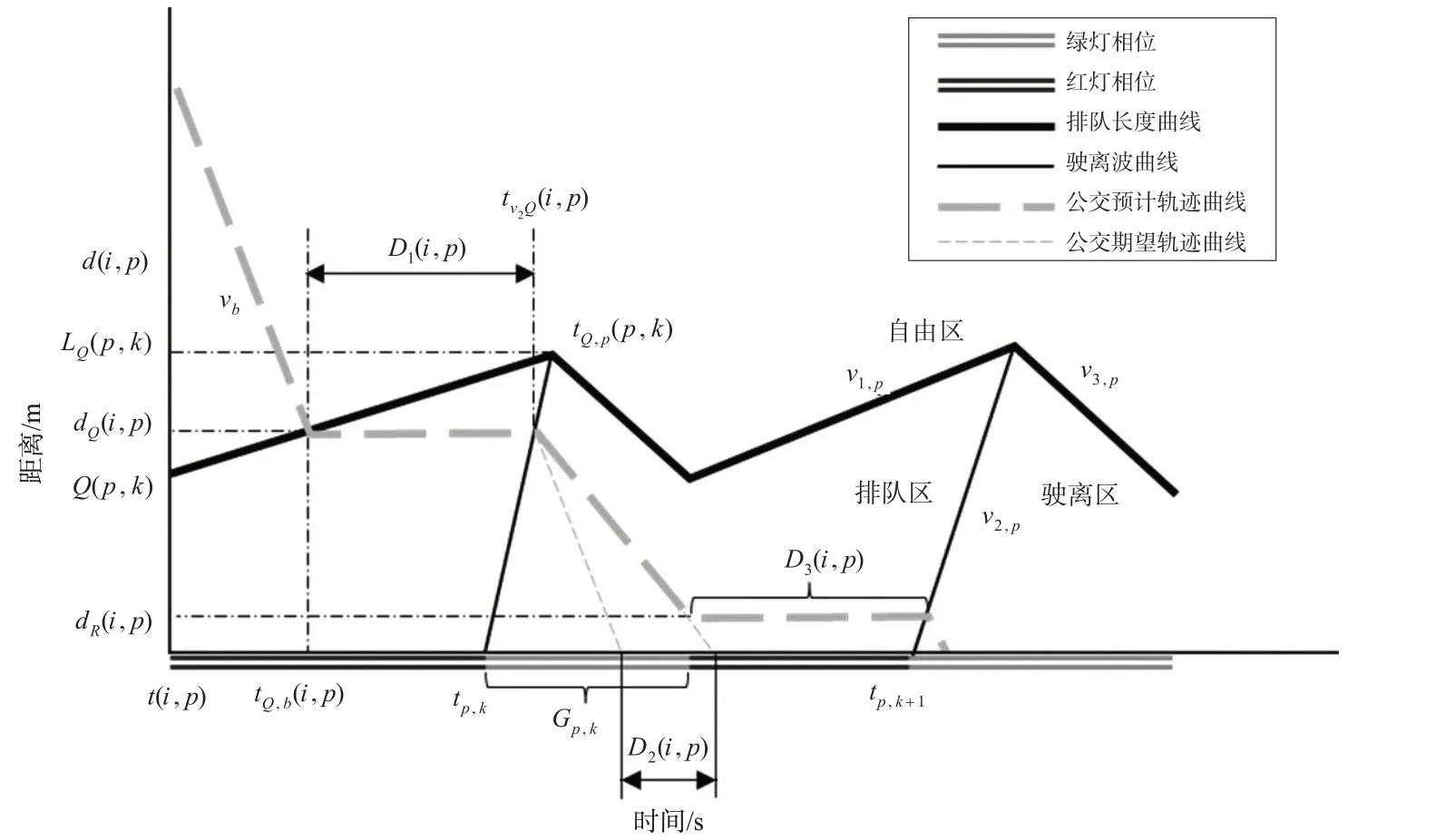
图2 公交车时空轨迹图Fig.2 Illustration of bus trajectory

公交车延误主要由停车排队等待延误D1(i,p)、驶离延误D2(i,p)和二次排队延误D3(i,p)这3个部分组成。定义θ1(i,p)，θ2(i,p)和θ3(i,p)为延误判定因子，用于判定延误计算时是否需要考虑上述类型的延误。

2.2.1 停车排队等待延误

停车排队等待延误D1(i,p)表示公交车i排队的停车等待时间（单位：s），表达式见式（9）。

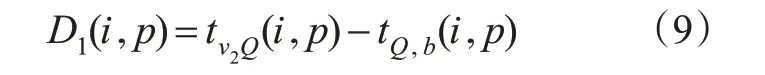
当tQ,d(p,k)＜tQ,b(i,p)时，排队消散结束早于公交车加入排队，公交车不会停车等待，θ1(i,p)=0；否则θ1(i,p)=1。

2.2.2 驶离延误

驶离延误D2(i,p)为公交车i分别以自由流车速和排队驶离车速通过停车线的时间差（单位：s），表达式见式（10）。

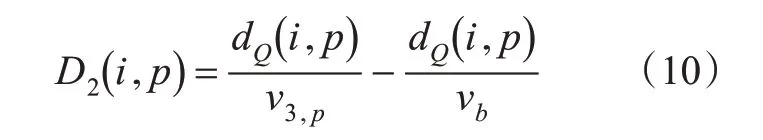
当vb＜v3,p时，公交车离开路口的速度小于消散波速，在离开路口的过程中不会受消散波影响，因此不产生消散波延误，此时，θ2(i,p)=0 。否则，θ2(i,p)=1。

2.2.3 二次排队延误

二次排队延误D3(i,p)表示公交车在下1 个周期离开路口与加入排队的时间差（单位：s），表达式见式（11）。

式中：dR(i,p)为公交车开始二次排队时到达路口停车线的距离，m。其表达式见式（12）。

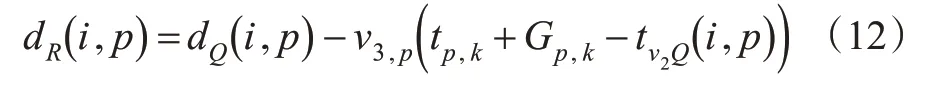
当tv2Q(i,p)+dQ(i,p)v3,p≤tp,k+Gp,k时，公交车在绿灯结束前通过交叉口停车线，不会产生二次排队延误，此时θ3(i,p)=0，否则θ3(i,p)=1。

公交车一般较少出现二次延误，但为了避免自适应控制过多改变相位绿灯时间进而导致某些相位通行权益受损的情况，延误估计过程依然考虑了二次延误的计算。

2.2.4 公交车延误表达式

将不同延误类型累加，得到单个公交车延误Dbus(i,p)，表达式见式（13）。

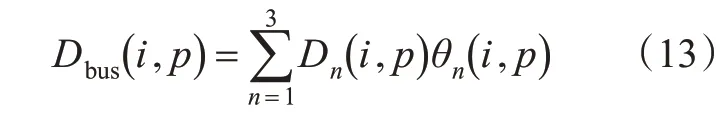
相位p的所有公交车延误见式（14）。

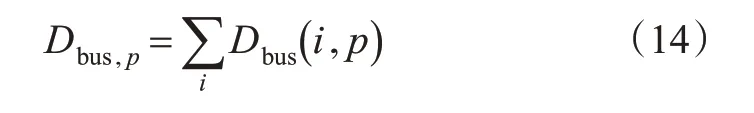
实际环境中，公交站台一般设置在交叉口下游，距离下1 个交叉口较远，而且驻站时间不可控因素较多，不易预测。因此，延误预估方法并没有考虑公交车驻站时间。

为了验证公交车延误预判方法的精度，分别选取低中高流量情况下的部分公交车进行测试，其预计延误与实测延误之差的均值、最大值和标准差的对比结果见表1。

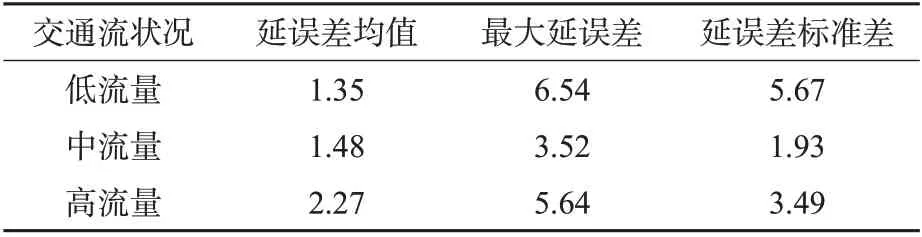
表1 公交延误预测精度表Tab.1 Bus delay estimation accuracy chart 单位：s

2.3 社会车辆延误计算

社会车辆数量较多，但单车的权重较低，且轨迹数据质量较差。为了降低边缘计算节点的运算压力，利用宏观交通流定数延误理论估计社会车辆的总延误[25]。

相位的时间-车辆数曲线见图3，横轴表示时间，纵轴表示车辆数，虚线为按极大似然估计值λ*p预估的累计到达车辆数曲线，点划线为累计驶离车辆数曲线。阴影部分为考虑车辆存在二次排队的情况下周期内到达的社会车辆延误计算区域。t1和t2分别是第k周期和第k+1 周期的红灯相位起始时间，t3是该部分车辆全部通过交叉口的时刻。

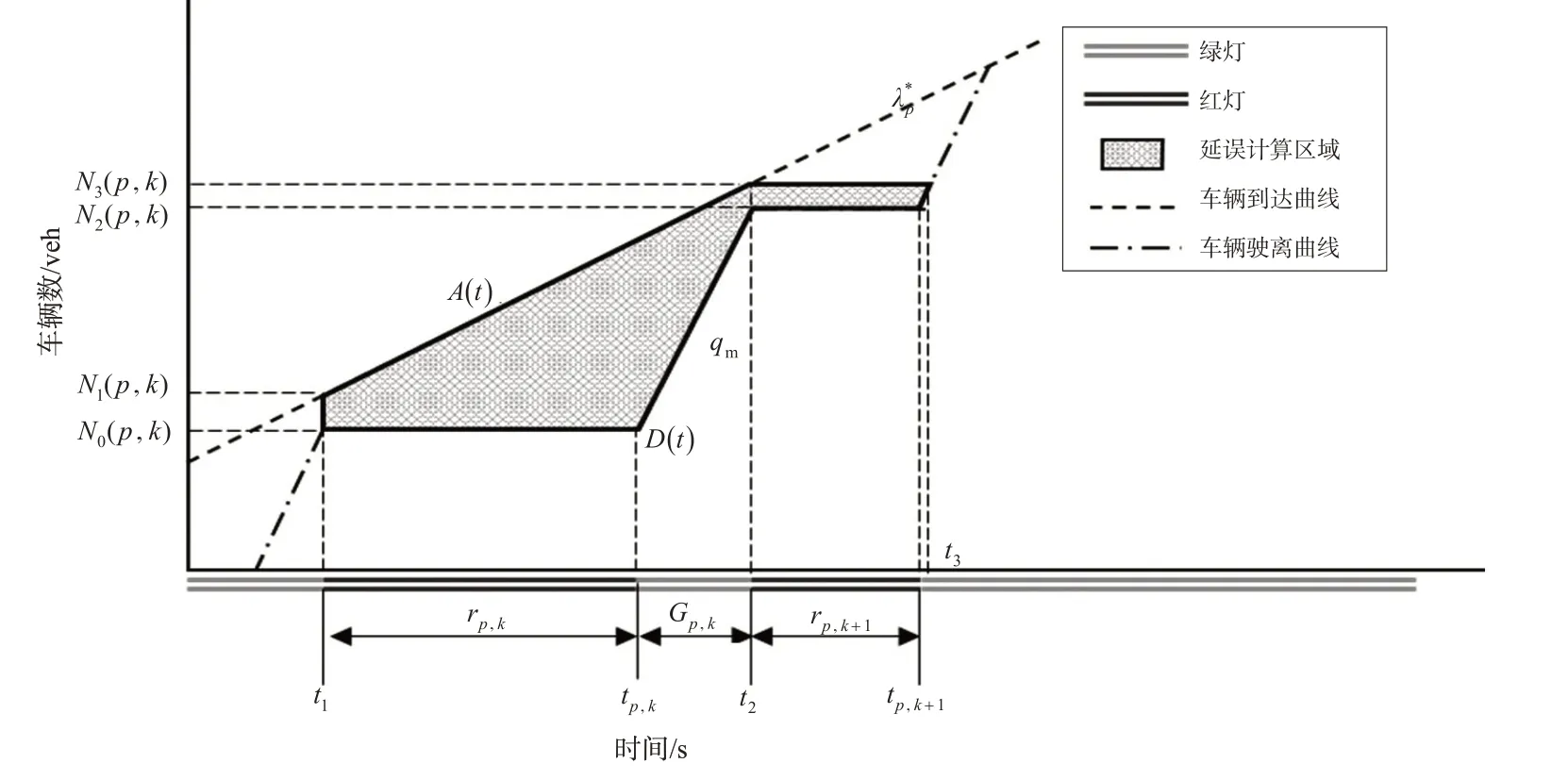
图3 时间-车辆数曲线图Fig.3 Time-vehicle number diagram

设A( )t为累计到达车辆数函数，其在第k周期附近的解析式见式（15）。

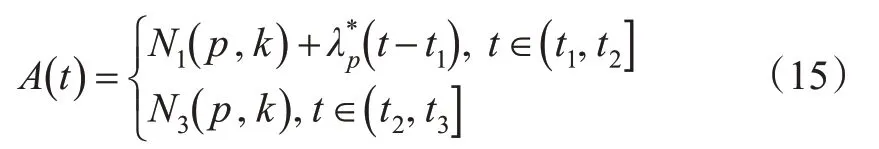
式中：N1(p,k)为第k周期相位p绿灯结束时累计到达车辆数，veh；N3(p,k)为下1个周期绿灯结束时累计到达车辆数，veh。

设D(t)为路口累计通行车辆数函数，解析式见式（16）。

f(t)为时间变量函数，解析式见式（17）。

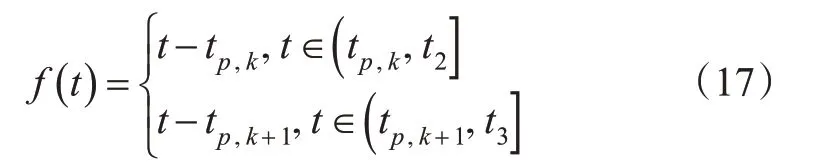
式中：N0(p,k)为第k周期相位p的红灯相位开始时累计驶离车辆数，veh；N2(p,k)为第k+1 周期相位p的红灯相位开始时累计驶离车辆数，veh。

计算阴影部分面积，则相位p的社会车辆总延误表达式见式（18）。

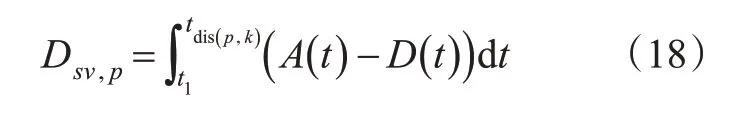
对于社会车辆来说，二次延误的情况出现得较少。但为了避免自适应控制过多改变相位绿灯时间进而导致非优先相位通行权益受损，延误估计过程依然考虑了二次延误的计算。

本研究中的公交车和社会车辆延误模型均未考虑全红相位对行驶轨迹的影响。虽然交叉口不设置全红相位可能会导致相位首车的行驶轨迹受到上1 个相位末车的影响而出现细微的变化，但在车流量较小、交叉口范围不大的情况下，此现象出现的概率较低，而且其轨迹变化较小，对延误预测的影响较小。

2.4 目标函数

选取公交车和社会车辆平均载客人数为加权因子构建交叉口加权总延误并将其最小化作为目标函数建立混合整数线性规划模型，其目标函数见式（19）。

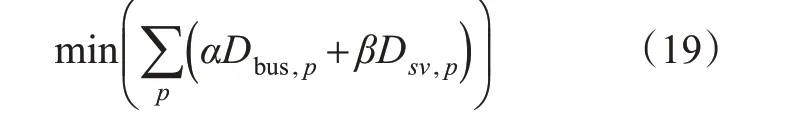
式中：α为公交车平均载客人数；β为社会车辆平均载客人数。

加权延误预测精度情况见表2，选取第5组实验第5 周期至第10 周期，分别记录第1 次计算时刻相邻相位的预计延误和实测延误并计算他们的比值。可见，预计延误比与实际延误比的值比较接近，策略的预计延误可以表征交通需求。

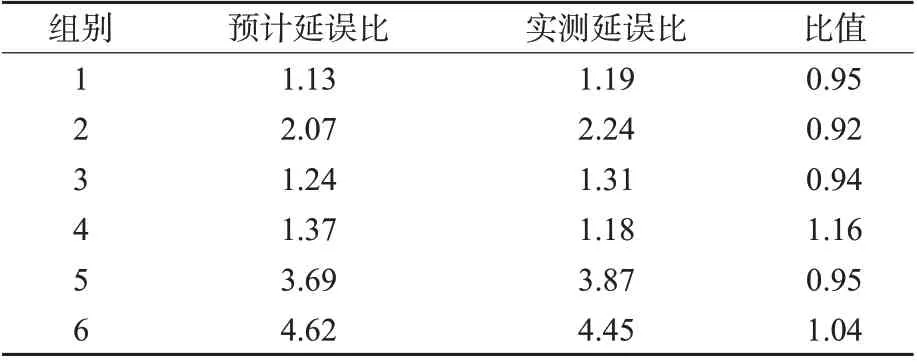
表2 加权延误预测精度表Tab.2 Weighted delay estimation accuracy chart

目标函数关于相位绿灯时长的分布并不规则，而且优化可行域为一维整数域，不便代入梯度计算，因此选用遗传算法geatpy求解器寻优。为保证寻得最优值，将其种群数量设置为10，最大迭代次数设置为20。由于单次延误计算耗时较长，而且迭代次数较多，因此整体寻优时间也较长，效率较低。

2.5 信控约束条件

验证算法所选的交叉口为4相位对称式十字交叉口，有以下约束条件。

1）周期时长和相位相序均不变，任意相位黄灯时间Yp,k为3 s，未设置全红相位。

2）任意相位绿灯时长Gp,k必须大于最小绿灯时长Gmin。

3）任意相位绿灯时长Gp,k最多只能与原配时绿灯时长Gp,o相差ΔGmax，以免非优先相位绿灯时长缩短过多影响其通行效益。

约束条件见式（20）～（25）。

3 算法验证

3.1 实验方案

选取武汉市车城北路与东风大道交叉口作为实验场地开展数据采集工作。该交叉口主干道东风大道为西南-东北向双向6 车道公路，次干道车城北路为西北-东南向双向4 车道公路，道路限速均为60 km/h。

采集不同时段（低流量、中流量、高流量状态）公交车及社会车辆流量数据作为输入，结合SUMO 仿真软件分别对不同级别交通拥堵状态条件下的算法性能进行验证[26]。交叉口实验场景见图4，其范围较小，满足延误模型的适用条件。本研究的自适应信号灯配时主要关注相位绿灯时长改变对排队车辆的疏解，因此采用SUMO 默认的Krauss 车辆跟驰模型约束车辆纵向运动[27]，相关参数见表3。

表3 仿真参数设置Tab.3 Simulation parameters

图4 实验场景图Fig.4 Experimental scenario

根据路口实际情况初始化信号灯配时及相序状态，权重系数设置参考交叉口附近的公交车和社会车辆的乘客数统计结果，其中，公交车延误权重系数α设为30，社会车辆延误权重系数β设为1.5。

实地采集的公交车和社会车辆流量数据共分为9组。基于采集时的交通流状态按照低流量、中流量和高流量进行划分，分别对应1～3组、4～6组和7～9组，其交通流量参数见表4。

表4 交通流量参数表Tab.4 Traffic flow parameters chart

3.2 数据分析

优化前后延误对比见图5。图5（a）为公交车单车平均延误，图5（b）为公交车周期平均延误，图5（c）为社会车辆周期平均延误，图5（d）为加权周期平均延误。

由图5 可见：不同拥堵状态下优化后的公交车单车平均延误均有所降低，低中高流量情况下其延误分别减少25.63%，25.25%，18.32%，平均降幅为23.07%。

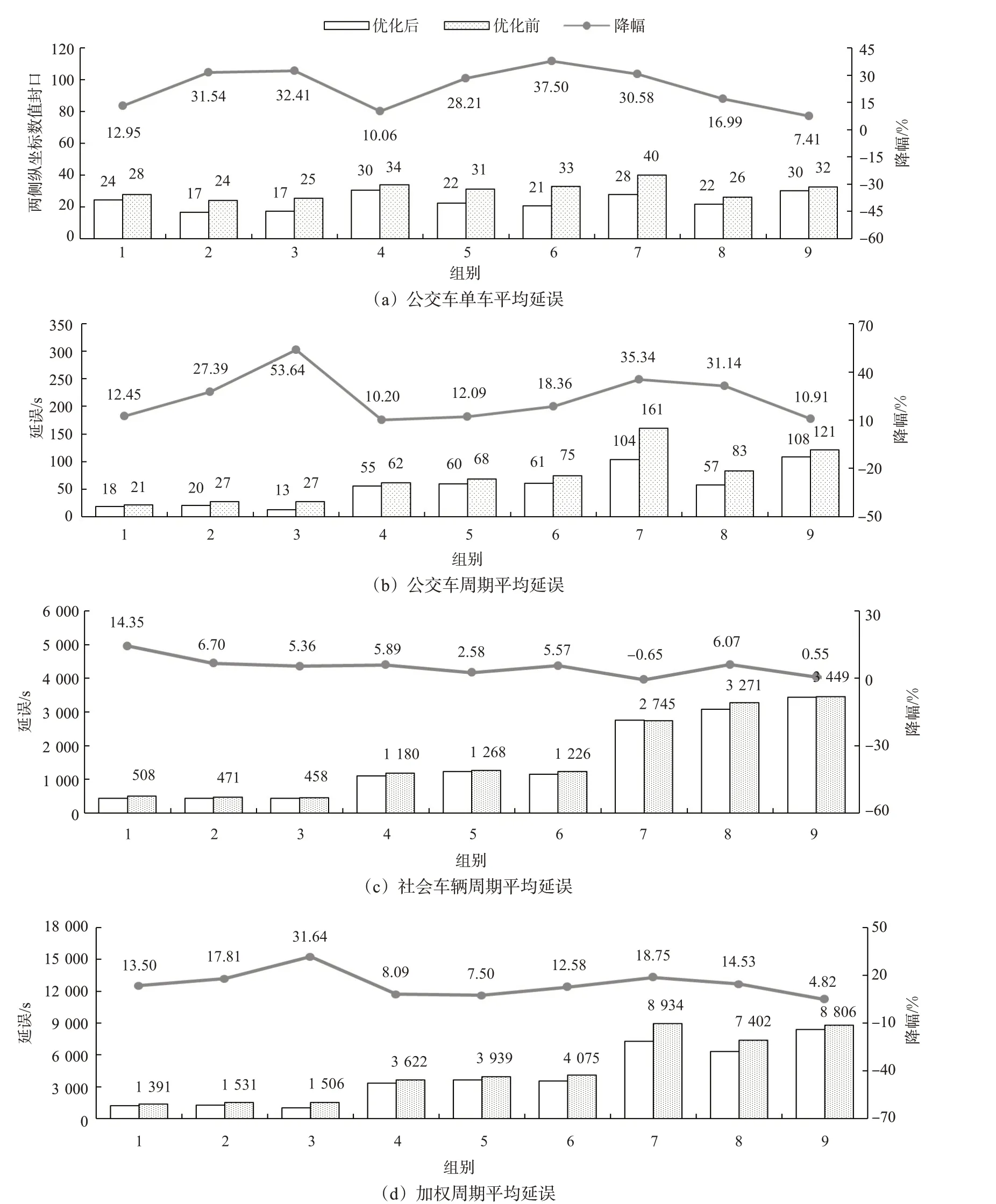
图5 优化前后延误对比Fig.5 Delay comparison of before and after optimization

公交车周期平均延误为每周期的公交延误之和的均值，所有组别均降低。其中，第3 组降幅最大，达到53.64%；第4 组降幅最小，为10.20%；平均降幅为23.50%；低中高流量情况下其延误分别减少31.16%，13.55%，25.80%。

社会车辆周期平均延误为每周期的社会车辆延误之和的均值，除第7 组增加0.65%外，其他组均下降。低中高流量情况下分别减少8.80%，4.68%，1.99%。

加权周期平均延误可近似视为每个周期乘客总延误的均值。所有组别均下降，低中高流量情况下其延误分别减少20.98%，9.39%，12.70%。

导致上述现象的主要原因是：低流量情况下，各相位的绿灯时长相对充裕，算法能为公交车所在相位分配更多的绿灯时长；中高流量情况下，各相位可供调整的有效绿灯时长较短，公交车延误的下降空间有限，非优先车辆的延误和加权延误的下降幅度也因此变小。

本策略的效益函数为加权延误，若流量没有超出策略工况，该值均会出现下降。公交车权重系数较大，因此每组的公交延误都有所下降。一般而言，公交车较多的相位也是车流量较大的相位，因此公交车延误明显下降的同时，非优先车辆通行效率也可以得到一定程度提高。但非优先车辆的权重相对较小，所以其通行效益有时不能很好被保证，如第7组的社会车辆延误就有少量增加。

综上分析，本策略在不同交通状态下具备广泛的适用性，可有效提升公交车运行效率，尤其在中低流量情况下，可有效帮助公交车和非优先车辆提升路口通行效率。由于策略考虑了非优先车辆通行权，本算法在中高流量情况下也具备较强的优越性，在优化公交车通行效率的同时，非优先车辆延误并没有大幅增加。

5 结束语

本研究以智能网联交叉口环境下的公交优先通行为场景，分别利用公交时空轨迹图和稳态延误模型预测公交车和非优先车辆延误，以此提出了一种基于混合整数线性规划的公交优先信号控制算法。

实验结果表明：本算法具备广泛的适用性，在中低流量情况下效果较好，即使在中高流量情况下，也能有效减少公交延误，提升公交系统的运行效率。同时，算法不会过多影响非优先车辆的正常通行，在大多数情况下甚至还可以辅助提升非优先车辆通行效率。

由于实验条件限制，本研究仅通过仿真软件进行了验证，而且延误预测模型并未考虑公交车驻站时间，方法还有待改进。