基于元胞自动机模型的路侧停车行为对交通流的影响研究*

张 月 孙立山 孔德文 张 鑫

（1.广州市城市规划勘测设计研究院 广州 510060；2.北京工业大学北京市交通工程重点实验室 北京 100124；3.北京市交通委员会政务服务中心（北京市船舶检验所） 北京 100124）

0 引 言

路侧停车是1 个由动态交通与静态交通共同组成的系统，二者相互影响，如果忽视了路侧停车的规划与管理，不仅难以有效缓解停车供需矛盾，反而会降低道路服务水平。统计发现，在城市中心区的高峰期，约有8%～74%的机动车驾驶员存在寻找路侧停车位行为，找到空闲车位的时间通常在3.5～14 min之间[1-2]。Chiara等[3]发现商用车辆（上下客，装卸货）停车频率更高，平均巡游时长约占总出行时间的28%，容易产生交通拥堵。因此有必要构建1个能有效反映实际路侧停车场景的仿真模型，从而为探究路侧停车行为的交通影响奠定理论基础。

国内外学者已经从不同方面开展了路侧停车影响研究，根据研究方法和研究范围的差异大致可分为3 类：①以单个路段为研究对象构建微观仿真模型；②以单个路段为研究对象构建微观数值模型；③以局部片区为研究对象构建数值模型。针对单个路段的微观仿真模型，高利平等[4]应用VISSIM仿真发现机动车流量是决定路侧停车交通影响程度的主要因素。郭宏伟[5]基于元胞自动机模型观测驶入车位数目和驶出车位数目对道路交通的影响，发现停车频率和停车耗时是主要影响要素。刘小明等[6]针对1 幅路可借用对向车道超车的场景，构建了停车频率、换道概率与交通流特性的关系。张月等[7]应用VISSIM 仿真分析了不同道路车位设置对路段延误时间的影响。Chen等[8]仿真分析了在不同非机动车道宽度下，路侧停车对非机动车的摩擦频率、阻滞频率和延误时间的差异。魏家蓉[9]、帅文磊[10]基于元胞自动模型分析了单向双车道下停车比例、停车耗时、停车位总长度对道路交通的影响。Krzysztof[11]构建了考虑驾驶员的耐心、感知能力、指示灯反应等特性的路侧停车元胞自动机仿真模型。关于单个路段的微观数值模型，裴玉龙等[12]以1幅路双向2车道路段为例，构建了路侧停车影响下的路段阻滞延误模型。邵长桥等[13]从车道宽度、侧向净空及车辆进出频率3 方面分别量化了路侧停车对通行能力的影响。战宇轩[14]针对停车位与交叉口的上下游关系，建立交叉口进口道的通行能力模型。对于局部片区的数值模型，Boyles 等[15]基于停车时长对泊位占用率的影响和停车巡游对交通流速度的影响，量化了停车时长与停车巡游之间的关系。Cao等[16]动态仿真了增加路侧停车位数目或限制最长停车时间对道路交通运行效率的影响。Geroliminis[17]应用宏观基本图方法，研究了在早高峰期间，路侧停车巡游行为对研究区域内所有车辆行程时间的影响。Arnott等[18]、Leclercq 等[19]建立了巡游距离与泊位占用率的关系。Millard 等[20]基于SFpark 项目，提出控制泊位占用率在60%～80%之间可减少50%的巡航交通量。

虽然众多学者已开展了路侧停车路段仿真建模，但在停车车辆对内外侧机动车车道的选择偏好，步行距离和前后空位数对车位选择的影响，停车车辆与通行车辆停驶特性的异同点等方面考虑尚有不足。笔者拟通过实际调研提取停车车辆行驶轨迹，并充分考虑停车车辆与通行车辆的交互作用，构建单侧双车道路段的停车仿真模型，模拟车辆巡游及驶入车位行驶轨迹，分析路侧停车行为对道路通行能力和行程时间的影响。

1 数据调查与分析

1.1 数据调查

停车路段的驾驶行为采集是建立仿真模型的前提，以城市中常见的2 幅路作为调查对象，包括2 条机动车道和1 条非机动车道，路段长400 m，车位数目20 个，其中机动车道宽度为3.5 m，非机动车道宽度为4 m，调查实景见图1。通过处理视频数据获取单个车辆的微观驾驶行为特性。

图1 道路示例Fig.1 The road sample of one-way two lane road

在轨迹处理中，以车辆运行方向为横轴的正向，由内侧机动车道至外侧停车位为纵轴的正向。因此不同车辆的原点坐标是相对的，距离目标停车位越近，横纵坐标越大。

在此主要描述车辆驶入车位行驶轨迹，因为驶离车位时通常会寻找合适的间隙以迅速换道汇入交通流，交通影响较小。

1.2 驶入车位特征分析

根据车辆驶入车位方式和占用机动车道时长的差异可分为：驶入连续空位和驶入单一空位。在此主要针对驾驶行为较为复杂的驶入单一空位过程开展分析。图2（a）～（c）依次表示不同时刻横纵坐标、车辆行驶轨迹和速度特征。表1为驶入单一空位时的关键坐标位置及各阶段耗时。

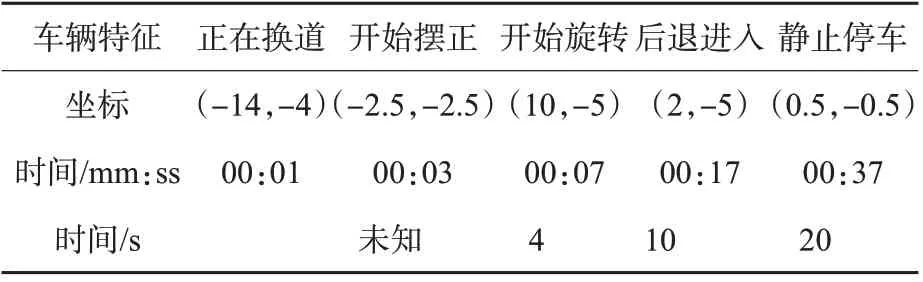
表1 车辆驶入单一空位时的关键点与时长Tab.1 Parking entry key points and usage time of only one space

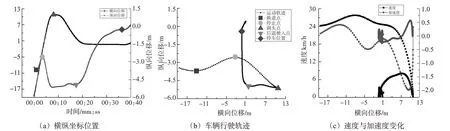
图2 车辆驶入单一空位时驾驶状态解析Fig.2 Parking status analysis of vehicles entering the parking space of only one space

2 路侧停车元胞自动机模型构建

由图2（a）～（b）可见：车辆在00：03时减速为0，坐标为（-2.5，-2.5），随后开始摆正车头位置，坐标为（10，-5），耗时10 s 后在00：17 找到后退进入车位的最佳角度，坐标为（2，-5），此时纵向位移最小值为-5 m，该过程外侧的机动车道，随后静止停放于（0.5，-0.5）。在图2（c）中，车辆寻找车位速度为24～26 km/h，在距离停车位20 m 处开始减速，直至最终达到停车位。

通过提取众多停车车辆行驶轨迹，发现车辆在驶入泊位前均会换至外侧机动车道；巡游速度与交通量和泊位占用率相关；在找到目标车位后，其驶入耗时受车位前后空间影响，当仅有1个空位时，驶入车位过程中旋转的角度更大，车辆会长时间占用机动车道，当有连续多个空位时，车辆能精准、迅速驶入停车，且几乎不占用机动车道。

在仿真系统中主要考虑通行机动车和停车车辆，二者运行状态和行驶轨迹存在差异，因此分别建立驾驶规则。非机动车灵活性较高，受停车车辆影响微弱，不作为研究对象。实际道路中驾驶过程复杂多样，难以完整复现。为此，通过实际观测、停车者访谈和经验借鉴做出一些必要性假设。

1）车辆在驶入车位状态时静止占用机动车道，占用时长为驶入车位耗时。

2）车辆在选择车位时，会综合权衡驶入车位耗时和步行距离。

3）停车车辆一旦处于驶入车位状态，最后必会进入车位内停放，不存在由于技术问题未进入车位内而离开的情况。

4）只有当停车车辆到达目标车位时，机动车才会驶入非机动车道。

5）车辆驶离车位时会打开转向灯，直行车辆根据转向灯持续时长决定是否减速或停车让行。

2.1 停车车辆驾驶行为特征分析

通过观测停车车辆在不同位置下驾驶行为的差异，将其分为以下8 种状态，即停车车辆状态ns=[1，2，3，4，5，6，7，8]，含义分别为进入路段、寻找车位、找到车位、驶入车位、静止停放、驶离车位、汇入车流和错失车位，各状态下具体驾驶行为特征见表2。

表2 路侧停车车辆状态划分Tab.2 Curb parking vehicle status division

停车车辆刚进入路段时，未观测到停车位，此时驾驶行为与通行车辆无显著差异，速度为正常速度。当目标车辆n能够看到路侧停车位时开始寻找车位，在该过程中，确定目标车位的具体规则如下。

1）明确可用车位集合。首先判断车位是否空闲，对于空闲车位，观测车位旁边有无车辆正在驶入该车位，若无，该车位可用，否则不可用；对于非空闲车位，判断车位内车辆是否正在驶离，若是，该车位可用，否则不可用。

2）计算空闲车位的驶入耗时。检测可用车位的障碍物边界，并将其折算为停车位数目，见式（1）；目标车位前后总可用长度决定了驶入车位耗时，根据实际调研情况将驶入耗时划分为3 个等级，具体关系见式（2）。

3）从空闲车位中界定可选择车位范围。主要包括2 个限定条件，即车位在前方观测距离范围内且没有其他车辆正在驶入车位。

4）从可选择车位中确立目标车位。计算驶入车位耗时与步行至目的地时间的总和，由于驶入车位过程的心理时间更长，因此对步行时间折减，见式（3）。总耗时最短的车位即为目标车位，见式（4）。

在车辆确定目标车位后，进入找到车位状态，车辆开始减速。由于元胞自动机模型的离散特性，车辆减速停止位置可能超越目标车位位置，因此要提前减速为0，随后转为驶入车位状态，即ns=4。

当车辆处于驶入车位状态时，在机动车道上的停止时间超过驶入车位所需时间tie，则车辆完成停车，即ns=5。

当车辆完成停放后，驶离车位并汇入车流，最终离开路段；但存在部分车辆行驶至停车位末端还没有找到车位，则错失车位，即ns=8。

2.2 通行车辆驾驶规则构建

1）跟驰规则。跟驰规则适用于车辆在同一车道且行驶方向一致，目标车辆前方有车辆行驶，在此采用姜锐等[21]提出的MCD 模型，主要包括加速、减速和随机慢化3个过程。车辆加速的条件为前车速度大于0，且前车未制动或与前车的车头时距大于安全时间间距。当目标车辆与前车间距较近，则根据有效间距采取减速措施。车辆随机慢化概率取值与前车是否刹车、车头时距和已经停止时间相关。

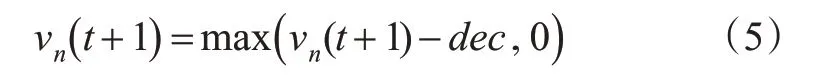
式中：vn为车辆n的速度，m/s；dec为车辆减速度，m/s2。

减速让行概率的计算见式（6），其中转向灯闪烁时长决定了基础让行概率，见式（7）。车辆汇入的影响距离阈值见式（8）。

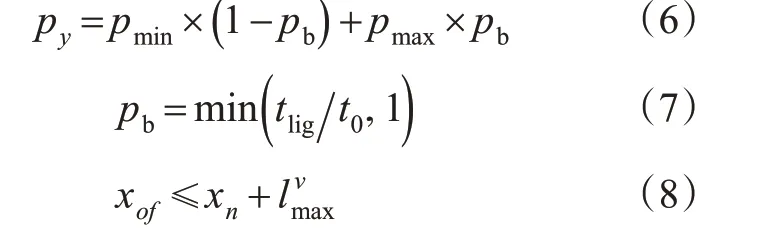
式中：py为车辆让行概率；pmin为最小让行概率；pmax为最大让行概率；pb为基础让行概率；tlig为汇入车辆转向灯闪烁时长，s；t0为受转向灯影响的时间阈值，s；xof为欲汇入车辆所在位置，m；为车辆汇入对后车影响距离的阈值，m。

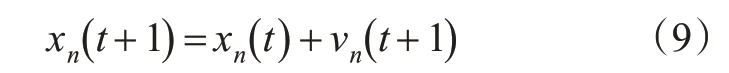
3）车辆位置更新。若车辆在内侧机动车道，则直接执行位置更新规则，见式（9）。式中：xn为车辆n的位置，m；xn(t+1) 为t+1时刻车辆位置，m。

在满足换道动机和安全条件时，相比外侧车道，通行车辆倾向于换至内侧车道，因此内外侧车道换道概率不同。

5）换道矫正。针对当前行驶于内侧车道，准备换至外侧车道的车辆修正。具体规则为：在换道影响距离内，检测是否有停车车辆正在向外侧车道换道。若有，判断随机数是否小于换道影响概率，若是，则取消换道。

2.3 停车车辆驾驶规则构建

1）跟驰规则：①加速规则。停车车辆加速规则与通行车辆一致，在寻找车位和找到车位状态时，加速度与最大速度的取值与其他状态不一致，具体参数在下文标定。②减速规则。与通行车辆的规则和参数取值一致。③随机慢化规则。与通行车辆的规则和参数取值一致。

2）驶入车位前速度修正。车辆在找到目标车位后，则会减速停车，按照元胞自动机模型离散的减速规则，其停止位置可能越过车位位置。因此与目标车位距离小于距离阈值时对速度修正，见式（11）。

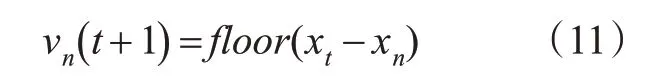
式中：floor为向下取整函数。

3）车辆汇入时速度修正。目标车辆行驶于外侧车道，内侧车道停车车辆或非机动车道上完成停车的车辆强制汇入当前车道时，根据其转向灯的持续时间和汇入车辆的速度，目标车辆决定是否让行，具体规则和参数取值与通行车辆一致。

4）车辆位置更新。车辆位置更新规则和通行车辆一致。

5）换道规则包括：①进入路段。车辆换道动机和安全条件均与通行车辆一致，仅换道概率不同，相比通行车辆，其更倾向行驶于外侧机动车道。②寻找车位。针对行驶于外侧车道的车道，换道动机为目标车道行驶条件能满足期望速度，即＞min(vn(t)+acc,vmax)，安全条件为于目标车道后车距离大于安全距离，即＞。③找到车位和驶入车位状态：此时不再向内侧换道，在机动车道上停止时间超过规定的驶入车位耗时则进入停车位内。④驶离车位状态。换道规则与通行车辆一致，但换道概率为1。即当停放时长超过指定停车时长，且满足换道条件，车辆必会驶出车位。在饱和条件下，目标车道后方车辆会根据其转向灯持续时长决定是否减速或停车让行。⑤汇入车流和错失车位状态。其驾驶行为和通行车辆完全一致，因此换道规则和换道概率与通行车辆完全一致。

6）换道行为修正。具体规则和参数取值与通行车辆一致。

3 仿真验证

3.1 仿真场景描述

数值模拟中，将系统长度设定为500个元胞，对应实际500 m 长的道路，路段包括2 条机动车道和1 条非机动车道，其中机动车道宽为3.5 m，非机动车道宽为4 m，路侧停车位设在非机动车道上，车位尺寸为6 m×2 m。为了实现机动车驾驶行为的精准建模，设置元胞尺寸为1 m×0.5 m，每条机动车道由7行元胞组成，非机动车道由8 行元胞组成，机动车占用5×4 个元胞，每个停车位占用6×4 个元胞。图3为仿真场景。在仿真系统中，采用开口边界条件。内、外侧机动车道每秒进车概率α分别取1 和0.6。路侧停车位起点在150 m处，终点在330 m，共计30个车位。

图3 路侧停车仿真场景示意图Fig.3 The schematic of curb parking simulation

3.2 仿真参数标定与验证

为验证仿真模型的有效性，根据实际调查和参考相关文献，将模型中用到的参数依次设置如下：在城市中心路段限速为40 km/h（约11.1 m/s）；停车车辆在寻找车位时的最高速度和加速度均小于正常车速，其他状态与通行车辆一致，见式（12）～（13）；车辆启动时加速度取运动中加速度的50%。驶入车位耗时与空位数目关系见式（14）。

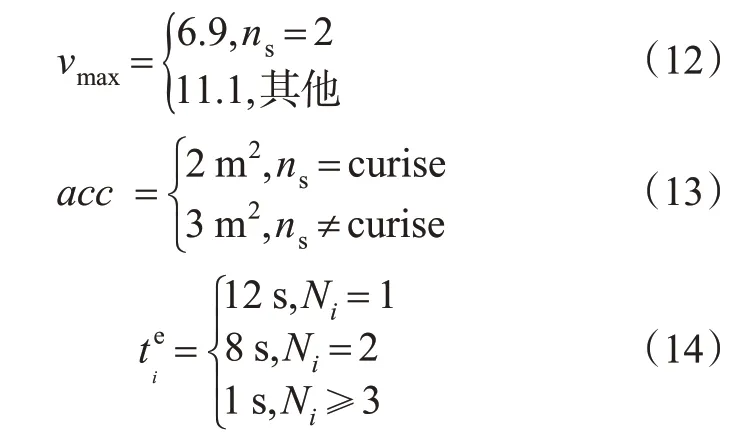
通过速度平均相对误差最小值标定得到通行车辆在内、外侧机动车道的换道概率分别为0.2和0.7，停车车辆在内、外侧机动车道的换道概率分别为0.8和0.3 时。而慢化概率、最小安全距离、停止时间阈值的取值参考《基于元胞自动机的交通系统建模与模拟》[22]，主要参数设置见表3。

表3 仿真模型中的参数取值Tab.3 Model parameters of rules used in simulation

应用12组调查数据对模型进行验证，得到速度平均相对误差见表4，统计速度平均相对误差值为5.8%，拟合度为77.6%，能较好的表征实际路侧停车路段车辆的运行规律，符合数据精度要求。

3.3 车辆巡游行为分析

时空图反应了单车道路段交通流的运行状况，水平轴是时间轴，纵轴是车辆的位置信息，有车地方为黑色点，无车地方为空白。设置停车需求强度为（0.15，15），即停车比例为0.15，停车时长服从均值为15 min 的指数分布，巡游速度为25 km/h，观测内侧车道和外侧车道车辆运行轨迹，分别见图4（a）～（b）。

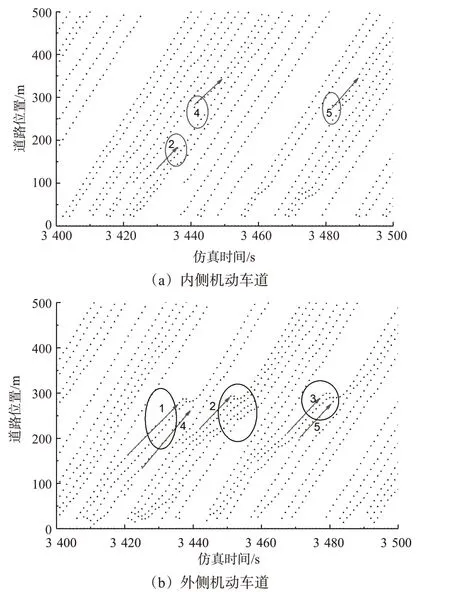
图4 车辆巡游轨迹图Fig.4 Trajectories of cruising vehicles

在图4（b）中，车辆1、车辆2 和车辆3 为待停车辆，分别在150，206，150 m进入巡游状态，巡游速度低于正常车速，后续车辆被迫减速。当内侧车道满足换道条件时，后续车辆会以一定概率换道，如在巡游车辆1后的车辆4和巡游车辆3后的车辆5分别在3 441 s和3 482 s换至内侧车道的277列和281列，见图4（a）。待停车辆2在3 436 s从内侧车道的183 m位置换至外侧车道，此时外侧车道后续车流辆被迫减速避让，从而产生排队延误，影响距离从189～292 m，约为100 m，影响时长达80 s，影响车辆数目共计4辆车。可见车辆强制换道和巡游过程是产生交通拥堵的重要原因，尤其在交通量饱和时，影响距离长，消散时间久。

3.4 车辆驶入车位行为分析

图5 为车辆驶入车位的轨迹图，图5（a）～（c）依次为内侧机动车道、外侧机动车道和非机动车道上运行时空图。

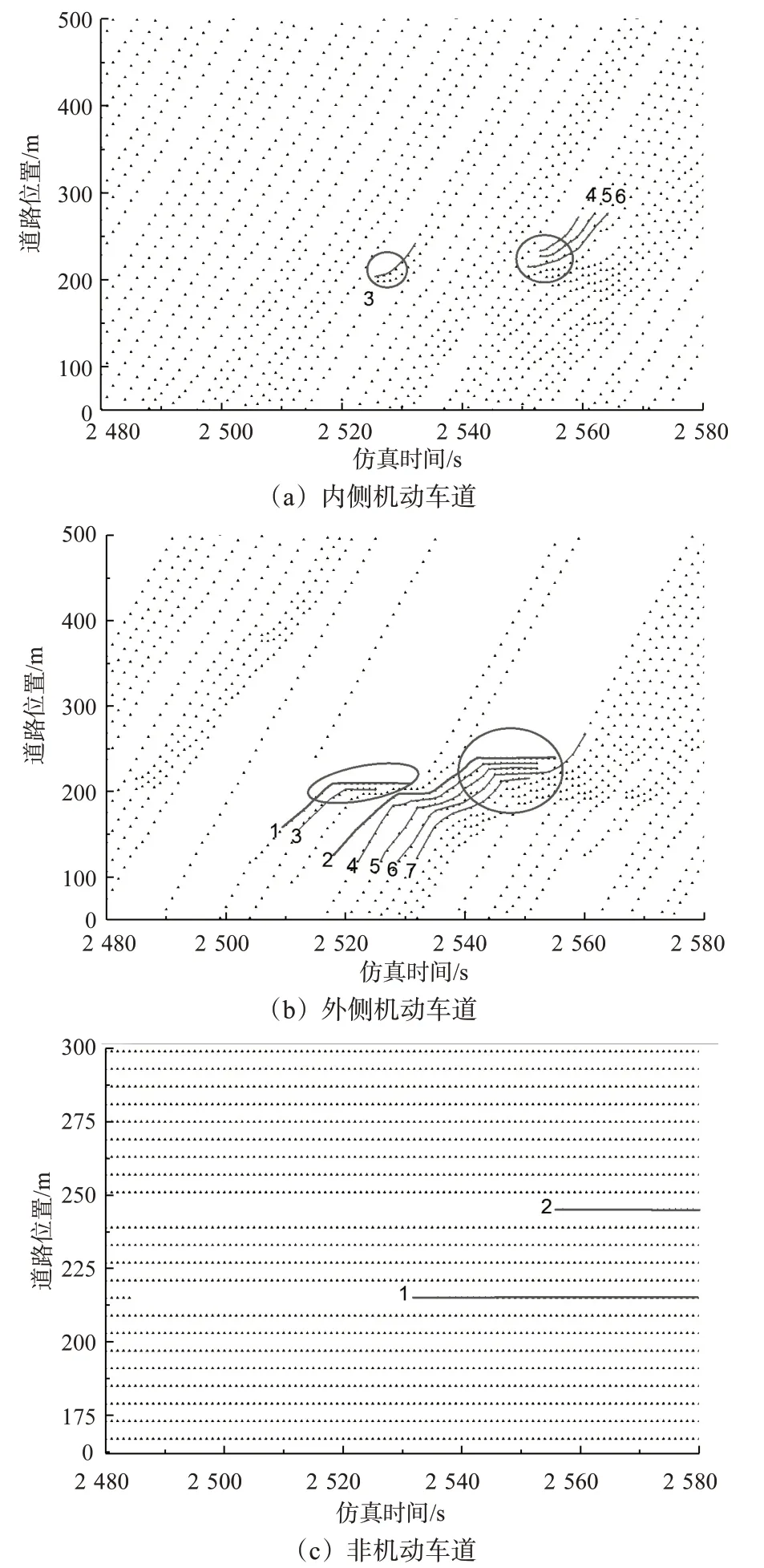
图5 车辆驶入车位轨迹图Fig.5 Trajectories of entering space vehicles

在图5（b）中，车辆1 和车辆2 为驶入车位车辆，分别在2 518 s和2 542 s到达目标车位，目标车位前后均无多余空位，驶入车位耗时为12 s，在2 530 s和2 554 s静止停放在215 m和251 m处，见图5（c）。在驶入车位过程中占用外侧机动车道，因此通行车辆换至内侧车道，如车辆1后的3号车，车辆2后的4号车、5号车和7号车，见图5（a），此时换道后造成内侧车流压缩，影响距离为190～230 m，影响时长为10 s。在图5（b）中，车辆2后的排队车辆数目较多，难以全部完成换道，则产生了道路交通拥挤，其影响范围在185～209 m，从2 542 s 开始排队，直至2 565 s 时完全消散。驶入车位过程对内外侧机动车道运行均会产生影响，影响程度与路段交通流量相关，在饱和流量下，停车车辆的换道行为更易导致交通拥堵。

3.5 路侧停车交通影响评估

1）车辆巡游对道路通行能力的影响。停车比例和停车时长共同决定了停车需求强度，将停车需求强度表示为（X，Y），其中停车比例为X，停车时长服从均值为Ymin 的指数分布，将停车需求强度划分为低、中、高3个等级，分别对应（0.05，5）、（0.1，10）和（0.15，15）。场景1、场景2、场景3的巡游速度分别为30，25，20 km/h，旨在实现不同停车需求强度下各要素的对照。不同停车需求强度下，巡游速度对交通流量的影响见图6。

当停车需求强度固定时，巡游速度对外侧车道的影响大于内侧车道，主要由于停车车辆多在外侧车道寻找车位；停车需求强度越高，巡游速度对流量的影响越显著。在图6（c）中，场景1和场景3的外侧机动车道分别在进车概率为0.8和0.6时达到饱和流量1 105 veh/h和513 veh/h。固定的巡游车辆数，巡游速度越高，道路通行能力越高。当巡游速度为20 km/h时，急剧降低了道路通行能力。

观测图6（a）和图6（b），停车需求强度为（0.05，5）和（0.15，15）时，从场景1 到场景3 外侧车道饱和流量分别减少96 veh/h 和245 veh/h；因为在需求强度低时，泊位能满足停车需求，巡游车辆数目少，提高巡游速度对道路通行能力无显著改善。

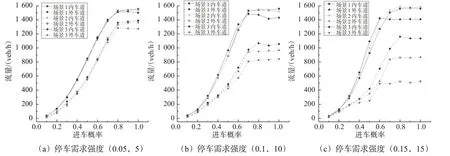
图6 巡游速度对道路交通流量的影响Fig.6 Traffic flow under different input flow and cruise speed

2）车辆巡游对行程延误时间的影响。差异的停车需求强度下，巡游速度对延误时间的影响见图7。在图7（a）～（c）中，场景2 的最高延误时间分别为28，69，94 s；固定的泊位供给下停车需求强度越大，巡游车辆数目增多，巡游速度对延误时间影响越大。在图7（c）中，场景1、场景2 和场景3 分别在进车概率为0.8，0.7，0.7 时达到最高延误时间为64，94，133 s。固定的停车需求强度，巡游速度越低，延误时间越长。在场景1 中，停车需求强度（0.05，5）与（0.15，15）的最高延误时间差值为25 s；在场景3中，停车需求强度（0.05，5）与（0.15，15）的最高延误时间差值为105 s。巡游速度越高，停车需求强度的增加对延误时间影响越小。在低、中、高停车需求强度下，场景1 与场景3 的最高延误时间差分别为10，15，105 s。因此在停车高峰期时，要限制巡游速度下限。

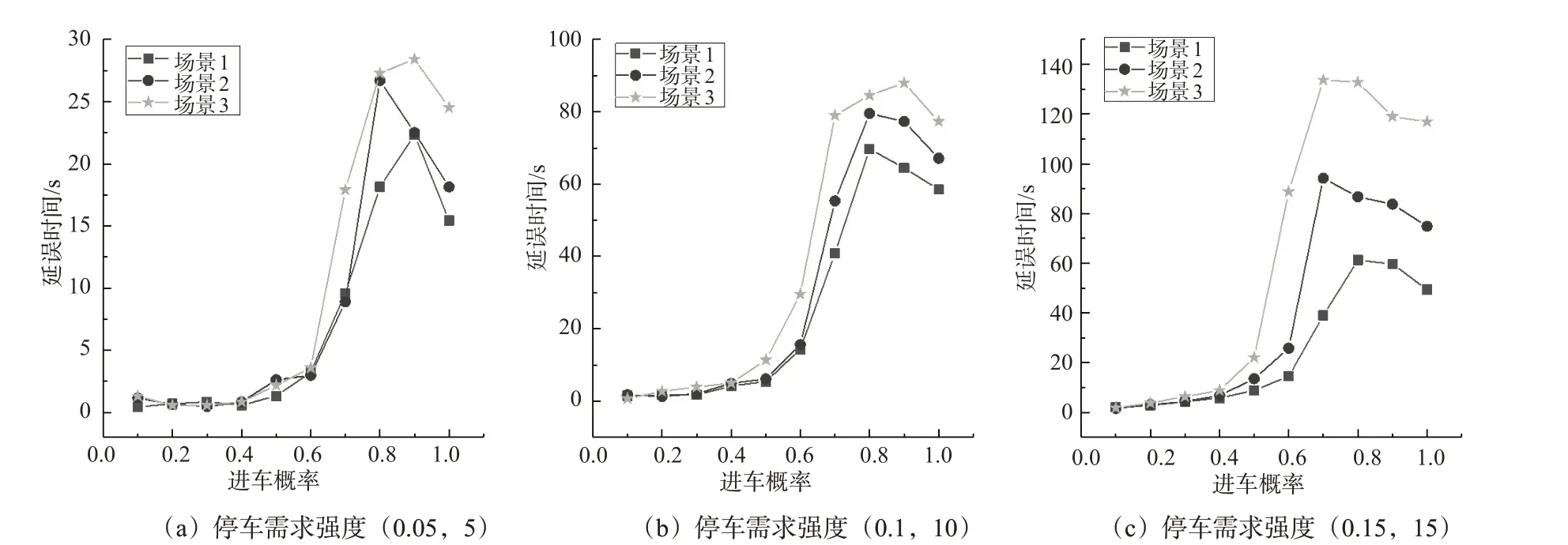
图7 巡游速度对延误时间的影响Fig.7 Average travel delay under different input flow and cruise speed

4 结束语

针对路侧停车场景，应用元胞自动机模型构建了单侧双车道仿真模型，模型中包含停车车辆和通行车辆，具体结论如下。

1）基于路侧停车车辆行驶轨迹，将停车过程细分为寻找车位、驶入车位、驶离车位等8类状态，并根据停车车辆和通行车辆的驾驶行为差异，从跟驰特征、速度矫正、换道规则等方面改进了路侧停车仿真模型。

2）通过实际道路数据对模型标定，经验证，拟合度为77.6%，说明能较好的模拟实际路侧停车行为。

3）通过仿真直观呈现了车辆巡游和驶入车位时的车流轨迹，发现停车车辆强制换道和低速巡游是产生交通拥堵的重要原因；停车巡游速度的提升能有效改善高停车需求强度下的道路通行能力，减少行程延误时间，因此在高峰期可以考虑限制最低巡游速度。

后续可继续分析停车位设置数目、停车需求量和停车时长等要素对路侧停车影响机理，提出路侧停车精细化管理策略，指导实际路侧停车规划与管理工作。