竖直降膜蒸发冷凝管内液膜流动特性研究

谢迎春，刘 军，徐 畅，蒋执俊，王宗满，李 玲，孙国强，黄达伟，马洪亭

（1.中核坤华能源发展有限公司，杭州 310000；2.天津大学 环境科学与工程学院，天津 300350）

0 引言

竖直管内壁面上的液膜流动现象，在化工、能源、医疗等领域十分常见，尤其是在强化换热器传热传质性能方面应用较为广泛。降膜流动具有传热传质系数大、温差小、热流密度高的优势［1］，且在较低流率与较低蒸发温度下即可拥有较高的传热系数［2］。NUSSELT 最早于1916 年就对仅考虑重力的层流降膜过程进行了理论分析，提出了液膜流动及传热机理［3］，之后又有很多学者通过理论计算、实验、仿真等不同途径对各种载体下的降膜流动过程进行了研究［4-15］，获得了如液膜流型、液膜稳定性、传热准则关联式等结果并对产生原因进行了讨论。但研究载体主要集中于降膜蒸发器这一形式，对降膜蒸发冷凝器研究较少。部分关于降膜蒸发冷凝器的研究，如陈良才等［16］对降膜蒸发冷凝器进行了仿真计算，主要研究了管束排列方式对降膜蒸发冷凝器的性能影响，但其形式为横管外布膜蒸发使管内流体降温。蒋翔等［17］对立式蒸发式冷凝器单管进行了CFD 模拟，研究了影响气相和液相间热质交换的因素，但气流组织形式为气液同向且研究工况单一。吴治将等［18］实验研究了气液逆向的蒸发式冷凝器，认为管中的弹簧插入物有利于提高设备传热性能，但缺乏相关模拟研究无法捕捉流动细节。张鹏其等［19］研究了管长、环隙宽度、空气入口宽度等对液膜流动特性的影响，但缺少空气入口速度对液膜稳定性影响的研究。

综上，目前关于管内降膜蒸发冷凝器方面的仿真研究还较少。根据蒋翔等［17］的研究，进入系统壁面的热流中，约80%被液膜吸收，而仅有20%的热量是通过气-液相界面使水分蒸发和空气温度上升，因此减少“干壁”［2］区域、保持液膜完整是十分必要的。本文在假定管壁为绝热的条件下，利用FLUENT 软件对气液逆向流动工况下竖直降膜蒸发冷凝管内液膜流动特性进行模拟仿真，计算了不同条件下管内壁成膜厚度、液膜稳定性等特性，主要研究了入口空气流速对不同喷淋密度时液膜覆盖程度的影响，确定合适的气、液入口参数，以避免“干壁”现象的发生。研究结果可以为降膜蒸发式冷凝器的设计和过程控制提供理论指导和科学依据。

1 计算模型建立

1.1 物理模型

管内降膜蒸发冷凝器结构如图1 所示，循环水泵将下部储水箱中的冷却水抽出，经冷却水管道流入竖管中，经过布液器后在竖直换热管内壁形成均匀水膜，并从换热管下部流出，汇集在储水箱中，形成冷却水循环。当水膜自上而下流过时与换热管内表面进行对流换热，对管外的气态工质进行冷却。与此同时，在冷凝器上部抽风机的抽吸作用下，来自周围环境的空气自下而上流过换热管中，一方面与水膜表面发生对流换热，同时由于空气为不饱和状态，在水蒸汽分压差的作用下，水膜表面的部分水分汽化后汇入空气流中，也会带走部分潜热并从上部排出。在管内对流换热和相变传热的共同作用下，实现对管外工作介质的快速冷却。

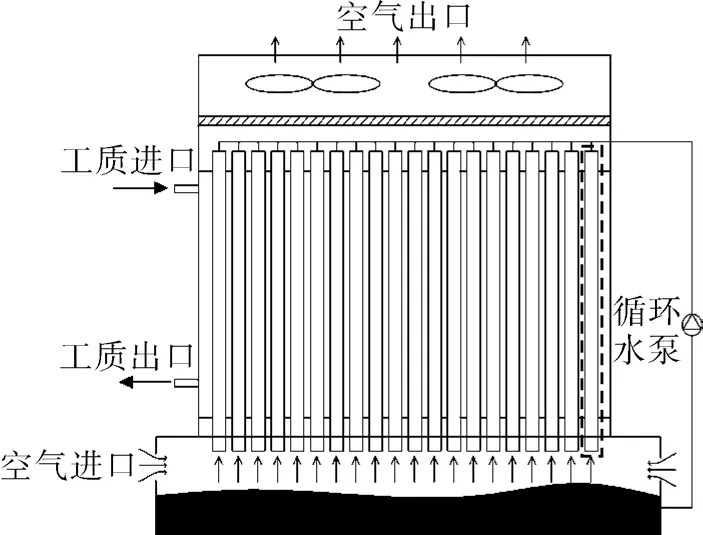
图1 降膜蒸发冷凝器结构示意Fig.1 Schematic diagram of falling film evaporative condenser

本文将对降膜蒸发冷凝器中单个竖直换热管内液膜流型、液膜稳定性等进行仿真模拟研究，如图1 中虚线框内部分，其放大后的结构如图2所示。

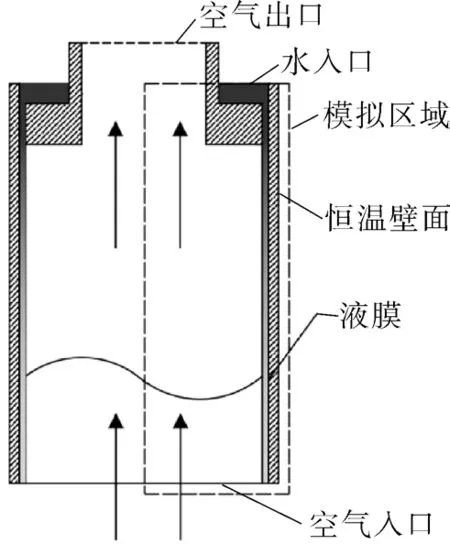
图2 冷凝器单管物理模型Fig.2 The physical model of single tube in the condenser

由于单管为规则的轴对称圆管且主要研究内容为液膜流动特性，因此可将其简化为2D 轴对称模型，模拟区域为图2 中矩形虚线框部分。为使液膜能够沿管内壁流动，本次模拟借助圆环型插件布膜器实现液膜的形成。水从单管上部进口流入，经分布器与壁面间狭缝的节流作用形成沿重力方向的贴壁液膜流动，空气从下部入口流入并从上部出口排出，形成逆向强制对流。

本模拟采用非稳态计算，对模型进行如下简化：

（1）圆管壁厚相较管径而言较小且对管内流动影响很小，因此忽略管壁厚度；

（2）假设壁面速度无滑移；

（3）假设流体均为不可压缩流体；

（4）假设管壁为绝热条件，不考虑与管外发生换热过程。

1.2 数学模型

本文采用计算流体力学软件FLUENT 对竖直单管进行数值模拟，研究竖直单管内气液两相逆流的液膜分布情况。针对本模拟中的多相流问题，采用VOF 模型，计算的控制方程涉及质量守恒方程、动量守恒方程。在降膜流动过程中，根据液膜流动特征选择湍流模型为RNG k-ε 模型，控制方程形式具体如下。

1.2.1 质量守恒方程质量守恒方程又称为连续性方程，表示单位时间内流体微元体中质量的增加等于同一时间间隔内流入该微元体的净质量。

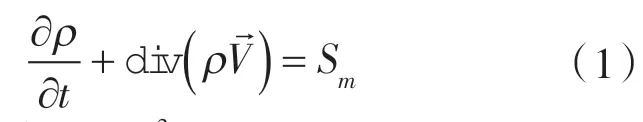
式中 ρ ——密度，kg/m3；

t ——时间，s；

div ——散度，m/s；

Sm——质量源相。

1.2.2 动量守恒方程

由于建立的是二维模型，只涉及到X，Y 2 个方向的动量，因此动量守恒方程如下：

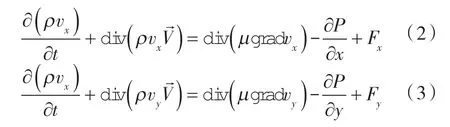
式中 vx——X 方向上的速度分量，m/s；

vy——Y 方向上的速度分量，m/s；

P ——流体微元体上的压力，Pa；

Fx——X 方向上的体积力，Pa；

Fy——Y 方向上的体积力，Pa。

1.2.3 湍流控制方程

RNG k-ε模型的湍动能k 和湍动能耗散率ε方程如下所示：

1.2.4 喷淋密度

喷淋密度用于衡量液体在管中的流量大小，其计算方法为液体质量流量˙m与管内径周长的比值，计算式如下：

对于圆管，液膜流动的雷诺数计算式为：

式中 Γ ——喷淋密度，kg/（s·m）；

μ ——液体的动力黏度，kg/（s·m）。

该模型下水入口流速对应的质量流量、喷淋密度及液体雷诺数见表1。

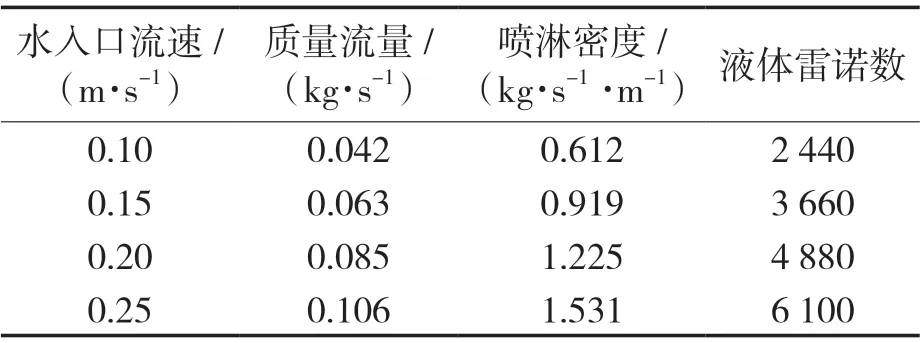
表1 水入口速度与对应的质量流量、喷淋密度及液体雷诺数Tab.1 The water inlet velocity and corresponding mass flow，spray density and liquid Reynolds number

1.3 边界条件与网格无关性验证

本模拟中管长1 000 mm，管径32 mm，以管段中间对称边界进行建模，建模区域为单管径向截面的一半，其中X 轴为管轴向方向，Y 轴为径向方向。如图3 所示，管道顶部入水口宽度为5 mm，设置为速度入口；液体通过宽为1.2 mm 狭缝后沿管壁流下形成液膜，管中央空气出口宽度为8 mm，设置为速度入口，速度方向与重力方向相反；下部管出口宽度为16 mm，设置为常压出口。管壁面设为无滑移壁面，厚度为0，接触角为90°。

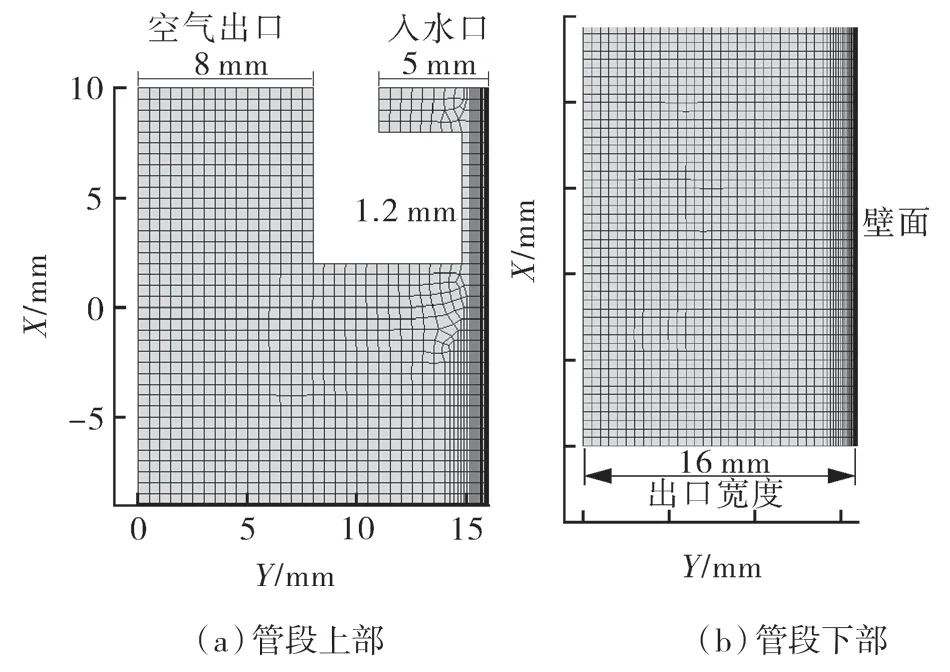
图3 网格划分与边界条件示意Fig.3 Schematic diagram of meshing and boundary conditions

网格划分采用非结构化网格，在近壁面区域设置膨胀层进行网格加密，通过计算入水速度为0.1 m/s 时不同网格数目下液膜厚度来进行网格无关性验证，结果如图4 所示。

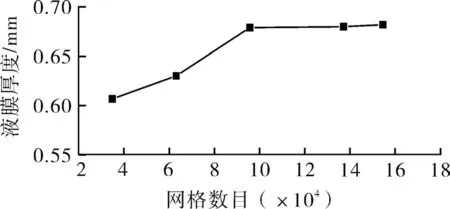
图4 网格数目与液膜厚度的关系Fig.4 The relationship between the number of grids and the thickness of the liquid film

综合考量计算精度与计算量，确定网格数目为95 730，此时设置采用近壁面2 mm 区域20 层膨胀层，生长率为1.1，能较好地捕捉液膜流动特性。

2 结果分析

2.1 管内自然通风条件下的液膜流动特性

图5 示出管内自然通风时不同入水速度下流动稳定时的液膜界面变化情况，气液交界面处为液相体积分数从100%至0 的薄层，其中以液相体积分数最接近50%的位置作为液膜边界来获取厚度。

图5 液膜界面位置分布Fig.5 Location distribution of liquid film interface

由图5 可以看出，在管内自然通风条件下，根据液膜厚度的变化可以将流动状态分为4 个阶段：起始段，稳定段，起伏段和波动段。以液体雷诺数2 440 为例，轴向坐标-52～10 mm 范围对应起始段，这一阶段液体离开狭缝后其厚度迅速由1.2 mm 降至0.68 mm，继而因重力贴壁下流，随后在轴向坐标-439～-52 mm 阶段形成如图6（a）所示的稳定段，此时由于液体流速较小空气剪切作用弱，液膜流动较为稳定，厚度维持在0.68 mm。轴向坐标-520～-439 mm 阶段对应图6（b）中的起伏段，该阶段空气扰动加剧，液膜厚度开始略有起伏，变化范围约为0.59～0.89 mm。流动进行至管段下部时形成图6（c）所示的波动段，对应轴向坐标-990～-520 mm，空气剪切力随着气液相速度差增大而增加，在重力、空气剪切力、表面张力等的共同作用下，液膜形成了峰前陡峭、峰后平缓的波浪状凸起。在无强制通风情况下，起始段，稳定段，起伏段和波动段平均占比6.1%，39.7%，8.3%，45.9%。

图6 降膜过程不同阶段的液膜形态Fig.6 Different stages of the falling film process

2.2 管内有强制通风条件下风速对液膜稳定性的影响

为了研究在风机抽吸作用下空气从管内自下而上流过时空气流速对液膜稳定性的影响，本文模拟计算了不同液体雷诺数与不同空气雷诺数下管内液膜的流动特性。结果表明，随着管内空气流速的变化，液膜稳定性会发生改变，但流动状态依旧可分为起始段，稳定段，起伏段和波动段4 个阶段。不同液体雷诺数在自然通风时与开始出现干壁现象时对应计算结果见表2。由于各工况下起始段变化很小，没有在表中列出，为了更简洁地表示各阶段的位置关系，仅列出了起伏段坐标，起伏段前部为稳定段，起伏段之后为波动段。

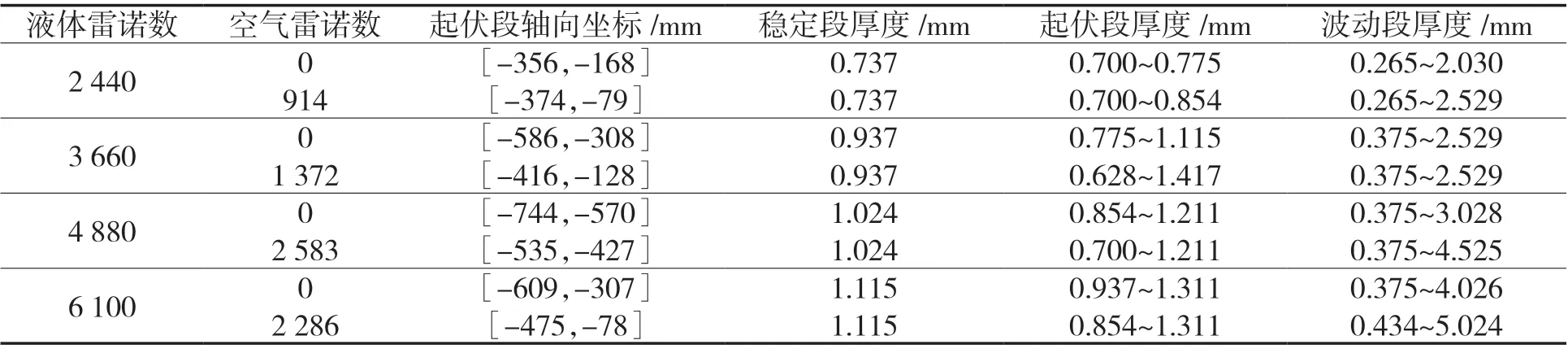
表2 不同工况下液膜流动状态汇总Tab.2 Summary of liquid film flow status under different working conditions

从表2 可以看出，不同液体雷诺数对应不同的稳定段厚度，该厚度随着液体雷诺数的上升而增加，在达到临界空气雷诺数之前，稳定段液膜厚度仅取决于液膜雷诺数而与空气雷诺数无关。在强制通风后，起伏段厚度与波动段厚度有不同程度的增加，这表明逆向气流使液膜波动程度增强。从波动段长度来看，无强制通风时，当Re液=2 440，3 660，4 880，6 100 时对应的波动段长度占管长比例分别为64%，41%，25%，38%，此时Re液=4 880 时液膜稳定程度相对较高；当以临界空气雷诺数强制通风时，对应的波动段占比变为了62%，58%，46%，52%，Re液=4 880 时的液膜依然相对稳定。以临界空气雷诺数通风时相比无强制通风时波动段平均延长了约11%，表明逆向强制通风强化了液膜的波动幅度，延展了非稳定段的长度，对于液膜稳定性影响较大。

此外，临界空气雷诺数并非为管内通风强度的上限，只说明当空气雷诺数高于此值时，在本模拟条件下竖管下部开始出现“干壁”现象，但大部分管壁依然能够覆盖液膜，临界空气雷诺数是体现最优液膜覆盖率的一种参考值。计算结果中Re液=6 100 的临界空气雷诺数相比Re液=4 880 有所下降的主要原因是：当液膜流量较大时，逆向气流与液膜交互时会使吹散量增加，散落在管中的液体加剧了气流的紊乱程度，使液膜整体变得不稳定，从而加剧了液膜飞溅程度，这种交互作用使得液体雷诺数较大的降膜过程难以承受较大空气流速。

2.3 液膜非稳定段形成原因

根据模拟结果，当空气流速超过临界值时，在管子下部出口就开始出现干壁现象。现以Re液=2 440，Re空气=1 142 工况下不同时刻的模拟结果来简要分析下部液膜稳定性变差的主要原因。图7（a）～（c）分别为2.1，2.3，2.5 s 时液膜的液相体积分数云图与X 方向分速度云图。

图7 Re液=2 440，Re空气=1 142 工况下不同时刻液膜流动状态与X 方向分速度Fig.7 The diagram of liquid film flow state and X-direction velocity under working conditions of Reliquid =2 440，Reair = 1 142 at different times

无强制通风时降膜过程稳定，管壁液膜覆盖率较高，而当强制通风达到一定强度后就会出现干壁情况。图7（a）反映了2.1 s 时管子下部液体前锋断裂的情况，此时管中已有部分散落液团，当逆向气流遭遇某些较大液团阻碍时，流道会变狭窄，此时从速度云图可看出液膜断裂处附近区域空气流速变大，这是由于节流效应使空气动能增大，压力能减小，这就容易破坏液膜前锋的受力平衡，使得下部液膜变形、破碎并散落至管中部，造成下部管壁处于无液膜覆盖状态。随着时间推进，2.3 s 时管中部散落液体量增多，如图7（b）所示。当降膜至2.5 s 时，从图7（c）可以看出，干壁的区域逐渐向管子上部扩展，在空气流速较大的区域伴随着新的液膜前锋的破裂，越接近干壁处的液膜由于逆向气流的冲击造成前锋面逐渐陡峭，波动幅度增强。

2.4 液膜流动速度

液膜流动速度是衡量液膜流动状态的重要参数，图8 体现了无强制通风与临界空气雷诺数2 种工况下Re液=4 880 时的液膜重力方向分速度（轴向速度）情况。降膜过程开始时由于重力、空气剪切力等作用在0～0.1 m 会呈加速度减小的加速运动。至0.15 m 后由于流速增大导致空气剪切力增大，液膜受力平衡接近匀速，但随着降膜过程的发展，在表面张力作用下液膜径向分速度大小与方向会发生周期性的变化，且变化幅度随着流动发展而变大［13］，这就导致液膜下部出现波动且波动幅度会随降膜长度逐渐增加，在重力方向分速度出现正负波动。当空气雷诺数为2 583 时，重力方向分速度的波动起点从降膜长度约0.65 m处提前至0.5 m 处，且波动幅度加大，表明强制通风对液膜稳定性具有显著影响。

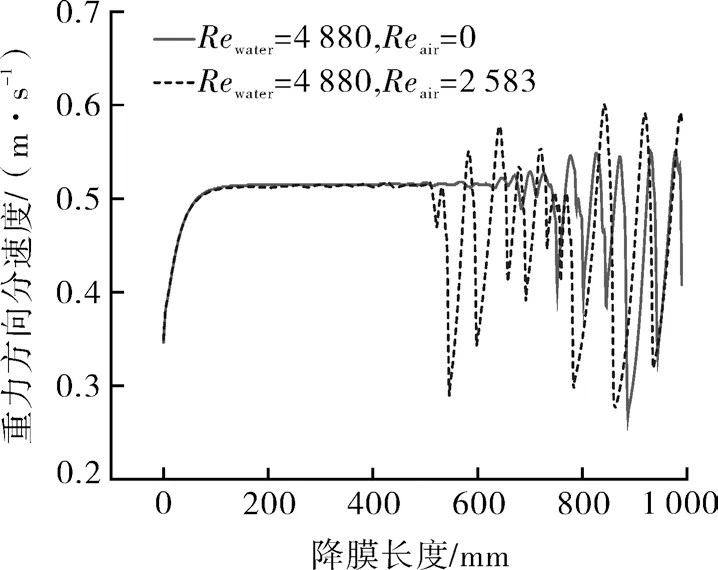
图8 轴向速度随降膜长度的变化情况Fig.8 The variation of axial velocity with the length of falling film

图9 示出了Re液=2 440，Re空气=914 工况下液膜流动状态与重力方向分速度间的关系。从图中可以看出，两者具有极强的关联性，在液膜厚度较大的位置即波峰处，对应的液膜分速度也较大，反之在波谷处分速度较小，重力方向分速度的变化情况与液膜流型密切相关。此外，随着降膜过程的发展，重力方向分速度波动会增强，波峰与波峰之间的间隔逐渐增加，重力方向分速度梯度则会逐渐减小。

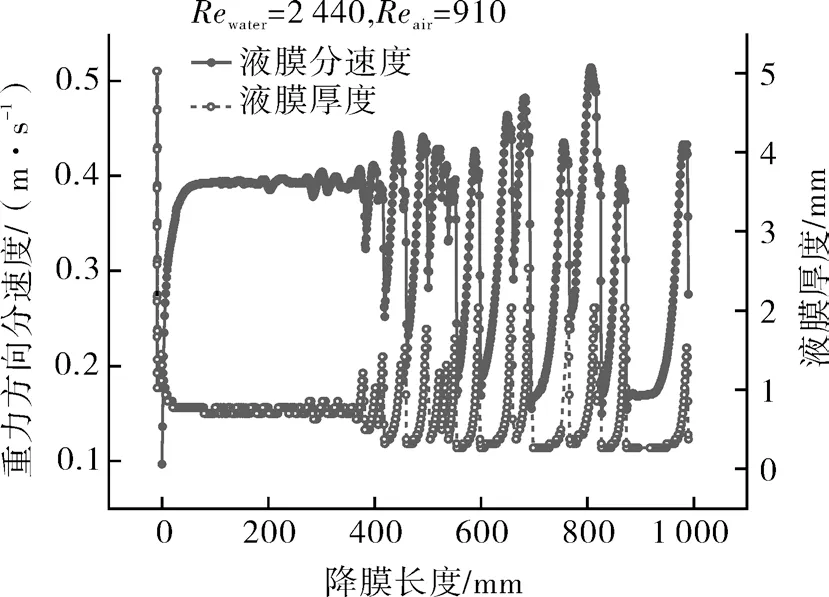
图9 轴向速度与液膜厚度随降膜长度变化情况Fig.9 The variation of axial velocity and liquid film thickness with the length of the falling film

2.5 理论计算与模拟结果验证

为了验证模拟结果的可靠性，本文还利用Wilke 推荐的关联式计算了不同入水速度下的液膜厚度，计算结果见图10 所示。根据文献［20-22］，液膜厚度可由如下方程进行计算：

图10 示出了不同入水速度下液膜厚度的理论值与模拟值。从中可以看出，模拟值高于Wilke理论值，这与上官闪闪、陈鑫等的研究结果一致［13，22］。本文计算范围内两者偏差为8.7%～17.2%，平均偏差为12.6%。偏差的出现可能来源于网格的细密程度、湍流模型的计算误差等，整体偏差处于合理范围内，表明模拟结果较为可靠。

图10 液膜厚度的模拟值与理论值对比Fig.10 Comparison of simulated and theoretical values of liquid film thickness

3 结论

（1）根据液膜流动状态，可以将竖管内降膜过程分为起始段、稳定段、起伏段和波动段4 个部分，无强制通风时4 阶段长度占比分别为6.1%，39.7%，8.3%，45.9%，而逆向气流扰动会改变四部分在管内的分布位置与范围大小。

（2）稳定段液膜厚度取决于液体的雷诺数，而与空气流动速度关系不大，但空气流动速度的增加会造成起伏段与波动段变化范围的改变，临界气体雷诺数下强制通风相比自然通风下的液膜波动段平均延长了11%。

（3）不同液体雷诺数对应各自的临界空气雷诺数，本文工况下临界空气雷诺数为914～2 583，当逆向空气雷诺数超过临界值后，液膜下部稳定性会遭到破坏，出现干壁现象。

（4）较高的液体雷诺数可能导致管道中部散落较多的液体，从而加剧逆向上升气流的湍流程度，造成干壁区域范围扩大；而较小的雷诺数则导致液膜较薄并使液膜的抗干扰能力减弱。根据仿真计算结果，液体雷诺数为4 880 时液膜稳定性较强。