空化效应下端面液膜机械密封性能分析

梁彦兵，丁雪兴，王世鹏，严如奇

（兰州理工大学 石油化工学院，兰州 730050）

0 引言

随着我国工业的不断发展，对工况条件的要求也愈加苛刻，高参数机械密封液膜空化现象对密封性能的影响愈发显著［1-2］，研究人员为设计合理的密封结构以提高密封性能，对螺旋槽液膜密封做了大量的研究工作［3-4］。

1980 年，NAU［5］对机械密封中的空化问题做了较为详细的研究，并通过试验的方法对这一现象进行了观测，预测结果与已知的试验结果一致，并指出气穴区域在航空航天、石油化工密封的应用中具有潜在用途。LEBECK［6］采用Elrod 算法研究了波度对密封环端面的影响规律，并对液膜的压力分布区域和空化位置进行了计算，发现该种结构的密封形式动静环端面温升变化微小、散热效果较好，有利于机械密封的长周期安全稳定运行。QIU等［7］通过对多孔端面机械密封的研究，将Reyonld 边界条件和JFO 边界条件的计算结果进行对比，发现二者存在较大的差距；并通过试验的方法对机械密封端面微孔的空化现象进行了观察，同时指出JFO 理论结合适当的算法可以预测织构中的空化现象，并给出了比其他边界条件更真实的性能参数。BRAUN 等［8］针对不同的空化形式进行了扩展，指出了3 种被广泛认可的液膜空化形式，提出了被广泛认可的空化形式。XUE等［9］针对螺旋槽机械密封油膜的空化问题，通过试验的方法在螺旋槽背风侧观测到空化现象，较大的空化区域会降低油膜的承载能力，同时指出气蚀效应对颗粒过滤器的分离特性影响很大。MA 等［10］对正、反向螺旋槽进行了研究，提出新槽型下空化抽吸槽的控漏机理并通过试验对这一机理进行了验证。

随着超高速流体机械的广泛应用，国内对空化问题也越来越重视。顾永泉［11］介绍了液膜中的空化效应，确定了机械密封性能的液膜空化边界条件和空穴区面积与位置的算法，并做了计算示例，但对流体膜的空化机理和空化冲蚀没有做深入的研究。随着空化效应研究的不断深入。潘晓梅等［12］建立了激光加工多孔端面机械密封的动压分析理论模型，应用有限元法求解了3 种不同空化边界条件下的雷诺方程，对空化算法和精度进行了比较，得出Reynolds 边界条件的预测速度优于JFO 边界条件的结论。钮建良等［13］针对LaserFace 液体润滑端面密封，采用混合接触理论，分析了LF-MS 的工作机理以及4 种不同端面结构的机械密封性能，提出LF-MS 具有动压效应好、摩擦系数低以及液膜刚度高等优点。赵一民等［14］对螺旋槽液膜密封的密封性能和端面润滑状态进行了研究，给出了优化结构参数并分析了润滑状态转变的规律。马学忠等［15-16］提出了液膜空化抽吸效应的概念，揭示了空化抽吸控漏机理，研究了高速螺旋槽端面液膜密封空化效应、流体惯性效应对密封性能的影响规律。WANG等［17-19］研究了微观表面以及密封动态特性对液膜密封空化效应的影响规律，得到了表面粗糙度、锥度以及动态特性参数对液膜中空穴促生和抑制影响的有限规律。冯瑞鹏等［20］通过研究不同参数对液膜汽化相变程度的影响，对液膜汽化相变后密封性能的变化规律进行了探索，最后得出液膜的汽化相变会对密封性能产生一定影响。到目前为止，对空化的研究主要集中在空化边界、空化对密封性能的影响及其演化特征等方面。然而，在高速泵的实际应用过程中工况参数和结构参数对空化效应的影响讨论较少，研究还不够深入。

本文基于典型的螺旋槽密封结构对液膜密封空化效应的诱发因素进行研究，通过流场模拟不同转速、入口压力、槽深、膜厚和螺旋角以探究液膜密封在变工况参数和变结构参数下对空化效应的影响规律，为今后空化效应的理论分析及结构优化提供依据。

1 端面液膜仿真模拟

1.1 端面螺旋槽几何模型

端面螺旋槽液膜密封二维平面结构示意如图1 所示。其中ro为外半径，rg为槽根半径，ri为内半径，α为螺旋角，h 为液膜厚度，hg为螺旋槽槽深，ω为旋转轴转速。

图1 螺旋槽液膜密封端面结构Fig.1 Structural diagram of spiral groove liquid film seal

动环密封面槽型采用经典螺旋槽槽型，其几何参数满足柱坐标系下的对数螺旋线方程：

式中 r ——端面气膜任意一点的半径，mm；

rg——螺旋槽槽根半径，mm；

θ ——展开角度，rad；

α ——螺旋角，rad。

1.2 端面液膜流场的基本假设

基于流体力学基本理论，考虑端面螺旋槽液膜密封的结构及工况参数，对端面液膜流场分析时，做出如下假设［21］：

（1）密封面间的流体为牛顿流体且其流动为层流、稳定流动；

（2）不考虑体积力对流场的影响；

（3）流体膜与密封机构的两端面间无相对滑移，忽略两端面间粗糙度的影响；

（4）忽略因工作过程中系统振动和动静环的变形对流场产生的影响。

2 计算模型

2.1 计算流体力学中的控制方程

基于空化效应的流体控制方程主要有：连续性方程、动量方程和气相传输方程［22］。

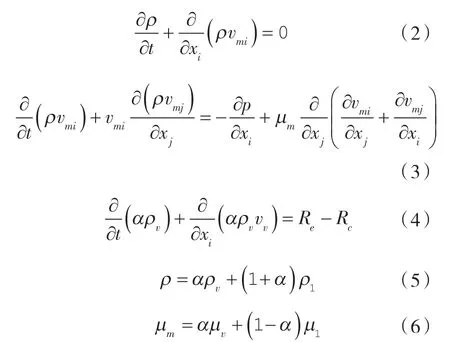
式中 ρ ——混合相的密度，kg/m3；

vm——介质平均速度，m/s；

Re——空化蒸发相；

Rc——空化冷凝相；

n ——相数；

v ——下标，气相；

l ——下标，液相；

α ——气相体积分数。

2.2 密封特性参数计算

（1）开启力为：

（2）泄漏率为：

2.3 网格划分

端面非接触式机械密封在运行过程中动、静环之间会形成一层较薄且开启力较大的流体薄膜，这层薄膜具有润滑、减震等作用，使密封系统稳定性提高。

计算域模型有如下3 个网格划分难点：

（1）液膜整体呈现似镰刀形，纵横跨尺度较大；

（2）当螺旋角较小时，螺旋线扭曲程度较大，网格质量难以达到要求，有时会出现负体积网格；

（3）由于对块进行了切分，所以需要通过辅助线对Block 进行映射。图2 所示为单周期液膜模型的建立、网格划分以及模拟计算的流程。

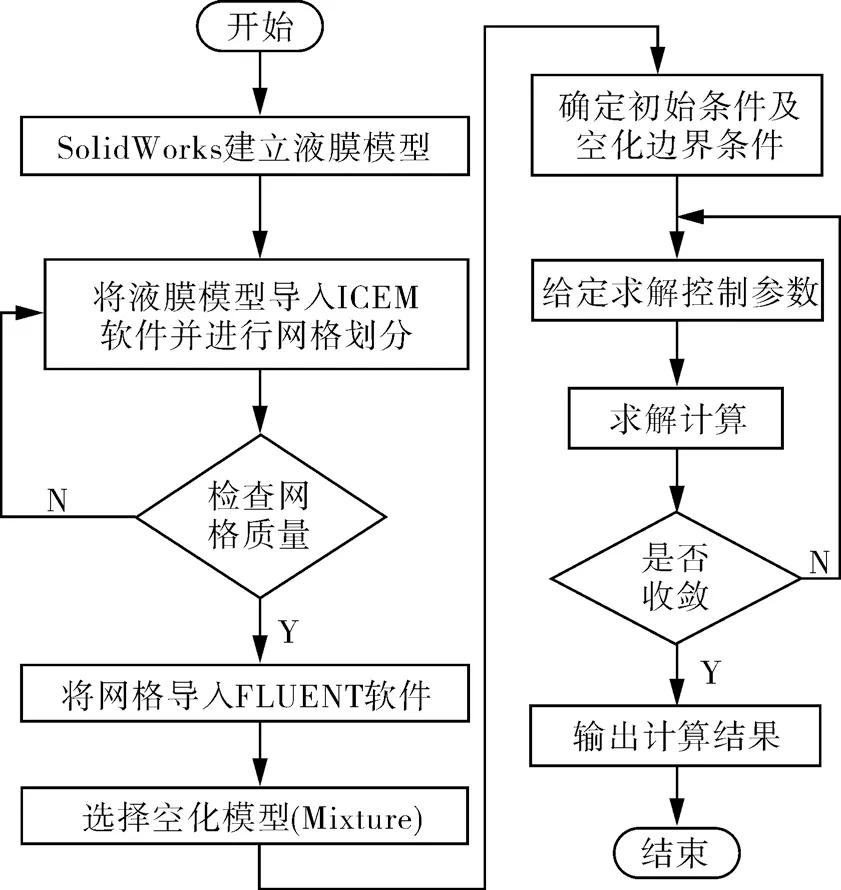
图2 液膜计算域模型网格与计算步骤Fig.2 Grid and calculation steps of liquid film calculation domain model

2.4 边界条件与求解器设定

用SolidWorks 软件建立端面螺旋槽液膜模型，密封液膜计算参数见表1。采用ICEM 软件对单周期模型进行网格划分，划分网格时分别进行周期性边界条件和各Part 的定义。图3 示出单周期液膜模型和液膜的周期性边界条件设定，将端面螺旋槽模型放大1 000 倍，以便于观察空化效应的形成机理。密封介质为水。将网格导入FLUENT 软件中，选择混合计算模型（Mixture），空化模型选择Schnerr-Sauer 模型，采用SIMPLEC算法并用有限体积法对扩散项进行离散，迭代精度设为1×10-6。

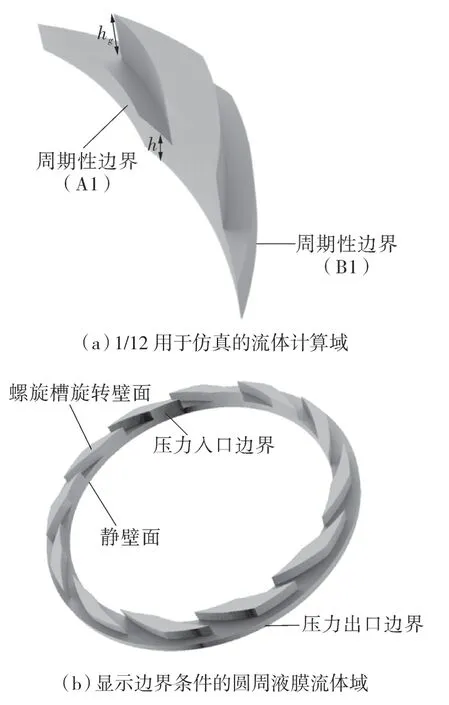
图3 轴向放大1 000 倍的液膜周期性边界Fig.3 Periodic boundary of liquid film with axial magnification of 1 000 times

表1 螺旋槽液膜密封几何参数Tab.1 Geometric parameters of spiral groove liquid film seal

2.5 网格无关性验证

网格数量分别选取了135 000，156 000，165 000 和185 000。计算域网格加密的区域为压力入口、压力出口和槽根附近。研究表明：网格数量从156 000 变化到185 000 时液膜的最大压力和流体的流速均未发生明显的改变，见表2。为了更加准确地获取空化细节、提高计算精度和加快收敛速度，文中选取的网格数量为165 000。

表2 不同网格数下液膜的最大压力Tab.2 Maximum pressure of liquid film under different mesh numbers

3 计算结果及分析

为研究敏感参数对空化效应和密封性能的影响，本文以经典螺旋槽为研究对象，对空化效应及密封性能进行模拟。以探究转速、压力、槽深、液膜厚度以及螺旋角对空化效应形成的影响规律。

3.1 转速的影响

选取转速为5 000～17 000 r/min，密封压力为0.8 MPa，其他参数不变，对密封端面间的液膜进行模拟计算。图4 示出转速为10 000 和17 000 r/min时的压力分布和密度比分布。螺旋槽由于其具有良好的流体动压效应在槽根部附近会产生系列高压区。由图可知，在螺旋槽外径侧产生周期性分布的低压区，低压区对应的区域为空化区，且随着转速的增加空化区域面积逐渐增加。

图4 不同转速下的空化压力及密度比分布Fig.4 Cavitation pressure and density ratio distribution at different rotational speeds

图5 示出考虑空化效应和不考虑空化效应下单个周期开启力和泄漏率的对比分析。由图可知，在转速从5 000 r/min 增加至17 000 r/min 时，考虑空化效应和不考虑空化效应的泄漏率存在一定的差异。在17 000 r/min 时，考虑空化效应的泄漏率比不考虑空化效应的泄漏率减小了6.7%；在5 000 r/min 时，泄漏率减小了4.4%。且随着转速的增大泄漏率呈现增大的趋势。这是因为当考虑空化效应的影响时，密封系统在运行过程中会在密封端面的液膜中形成一团空化气泡，气泡内部的压力低于外部压力，随着运行过程的进行空化气泡发生溃灭，密封间隙的高压流体会立刻补充到低压空化气泡的位置，从而减少密封介质的泄漏。而此时的开启力也会因为高压区域向低压区域的补充而下降，所以同时导致开启力低于不考虑空化效应下的开启力，且开启力最大差值为148.9 N，开启力减小了7.3%。

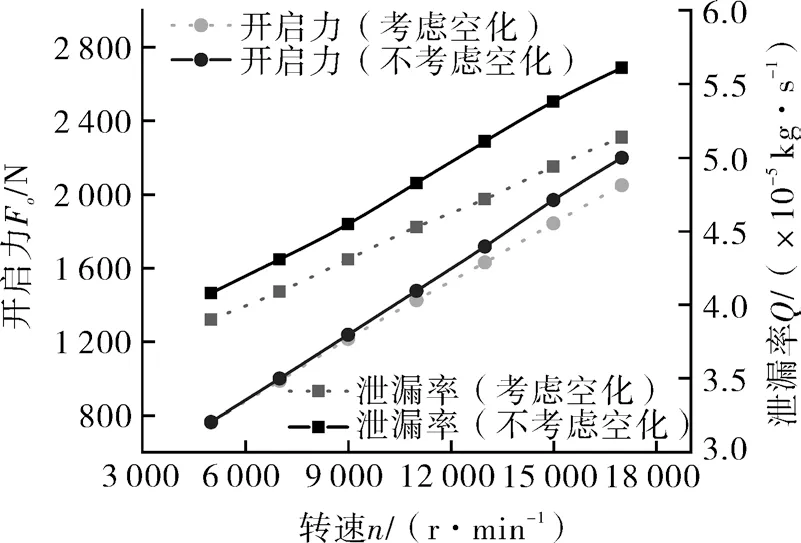
图5 转速对密封性能参数的影响Fig.5 Effect of speed on sealing performance parameters

3.2 压力的影响

本文中选取密封压力为0.2～1.8 MPa，转速为15 000 r/min，其它参数不变，对密封端面间的液膜进行模拟计算。图6 示出密封压力为0.2，0.6 MPa 时流体膜压力及密度比分布，在螺旋槽外径侧产生周期性分布的低压区，低压区对应的区域为空化区，且随着密封压力的增加空化区域面积逐渐减小。

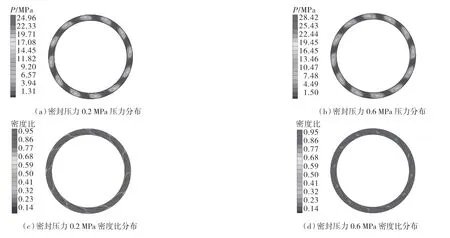
图6 不同密封压力下空化压力及密度比分布Fig.6 Cavitation pressure and density ratio distribution under different sealing pressures

图7 示出考虑空化效应和不考虑空化效应下单个周期开启力和泄漏率的对比分析。

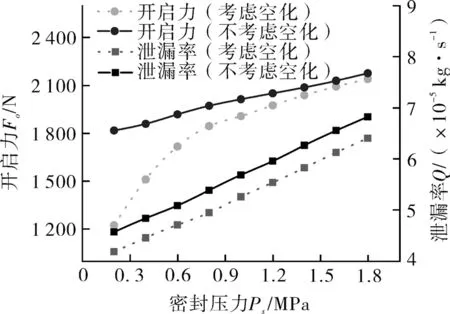
图7 密封压力对密封性能参数的影响Fig.7 Effect of sealing pressure on sealing performance parameters

由图可知，随着密封压力的增加开启力和泄漏率都呈递增趋势。但是考虑空化效应下的开启力和泄漏率均低于不考虑空化效应下的值。泄漏率随着压力增加其变化趋势基本一致，最大差值为4.4×10-6kg/s，变化率在7.6%左右浮动；当压力为0.2 MPa 时，开启力的变化最大，最大差值为594.7 N。开启力随着密封压力的增加考虑空化效应下的增长趋势开始较快后来逐渐减慢，这是因为随着密封压力的增加空化气泡形成变得越来越难，即空化区域越来越小，空化气泡溃灭后高压区域向低压区域补充的部分减少，所以开启力的变化也就不那么明显了。泄漏率也和开启力一样，具有相同的原理和规律。

3.3 螺旋角的影响

选取螺旋角为12°～50°，转速为15 000 r/min、密封压力为0.8 MPa，其他参数不变，对密封端面的液膜进行模拟计算。图8 示出螺旋角为18°和20°时流体膜压力及密度比分布，在螺旋槽外径侧产生周期性分布的低压区，低压区对应的区域为空化区，且随着螺旋角的增加空化区域面积逐渐增大。

图8 不同螺旋角下的空化压力及密度比分布Fig.8 Cavitation pressure and density ratio distribution under different helix angles

图9 示出考虑空化效应和不考虑空化效应下单个周期开启力和泄漏率的对比分析。

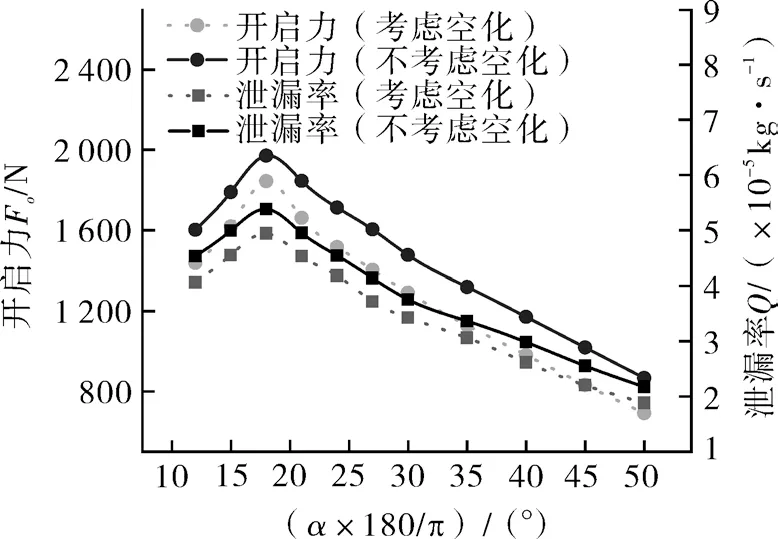
图9 螺旋角对各密封性能参数的影响Fig.9 Effect of the helix angle on each sealing performance parameter

由图可知，随着螺旋角的增大，开启力和泄漏率呈先增大后逐渐减小的趋势。且考虑空化效应的开启力和泄漏率均低于不考虑空化效应的值。随着螺旋角的增大，考虑空化和不考虑空化的变化趋势相同，且泄漏率最大差值为4.3×10-6kg/s，开启力的变化趋势与泄漏率一致，都控制在14.3%之内。随着螺旋角的增大，“细长型”的螺旋槽逐渐变成“扇形”槽，使得动静环端面的剪切速度和螺旋槽侧壁法线方向的夹角减小，所以沿周向膜厚的发散程度加大，导致空化现象更显著。但是增大的液膜空化区也导致了螺旋槽的泵送能力和流体动压效应减弱，进一步改变了液膜的承载力和密封泄漏率，在螺旋角为15°～20°时，整体密封性能最好。

3.4 槽深的影响

选取螺旋槽槽深为2～18 µm，其他参数不变，对密封端面的液膜进行模拟计算。图10 示出槽深为6，12µm 时流体膜压力及密度比分布，在螺旋槽外径侧产生周期性分布的低压区，低压区对应的区域为空化区，且随着槽深的增加空化区域面积逐渐减小。

图10 不同槽深下的空化压力及密度比分布Fig.10 Cavitation pressure and density ratio distribution under different groove depths

图11 示出考虑空化效应和不考虑空化效应下单个周期开启力和泄漏率的对比分析。由图可知，随着槽深的增大，流体动压效应先增强后减弱，开启力和泄漏率先增大后缓慢减小。当槽深等于12 µm 时，开启力和泄漏率达到最大值。但是在考虑空化效应时的开启力和泄漏率均小于不考虑空化效应时的值。泄漏率在18 µm 时出现最大差值，其值为5.4×10-6kg/s；考虑空化和不考虑空化时开启力的变化趋势基本一致，最大差值为132.9 N。且随着槽深的增大，密封间隙中的阶梯效应越来越明显，在螺旋槽的根部密封介质对槽的撞击作用加强，所以导致了最大压力的出现。但是随着槽深的不断增加，槽深不会再对密封压力产生明显的影响，所以开始出现了缓慢下降的趋势，从这一结果可以反映出过大的螺旋槽槽深反而会对密封性能产生不利的影响，在槽深为10～14 µm 时，整体密封性能最好。

图11 槽深对密封性能参数的影响Fig.11 Effect of groove depth on each sealing performance parameter

3.5 膜厚的影响

选取液膜厚度为2～6 µm，其他参数不变，对密封端面的液膜进行模拟计算。图12 示出膜厚为3 和6 µm 时流体膜压力及密度比分布，随着膜厚的增加槽区流体的剪切作用减小，空化区域面积也开始减小。

图12 不同膜厚下的空化压力及密度比分布Fig.12 Cavitation pressure and density ratio distribution under different film thickness

图13 示出考虑空化效应和不考虑空化效应下单个周期开启力和泄漏率的对比分析。由图可知，随着膜厚的增大，流体动压效应减弱，开启力逐渐减小，泄漏率出现了相反的趋势，即随着膜厚增大泄漏率也逐渐增大。且考虑空化效应时的开启力和泄漏率均小于不考虑空化效应时的值。开启力和泄漏率的变化趋势相似，随着膜厚的增加考虑空化和不考虑空化的泄漏率及开启力出现了明显变化，泄漏率的最大减小率为29.4%；2 种工况下开启力的差异变化范围为5.9%～12.5%。随着膜厚的增大，端面间隙增大，泄漏通道变大，所以导致泄漏率持续增大。与此同时流体的动压效应减弱，密封端面的开启力开始出现了持续减小的趋势，在膜厚为3～4 µm 时，整体密封性能最好。

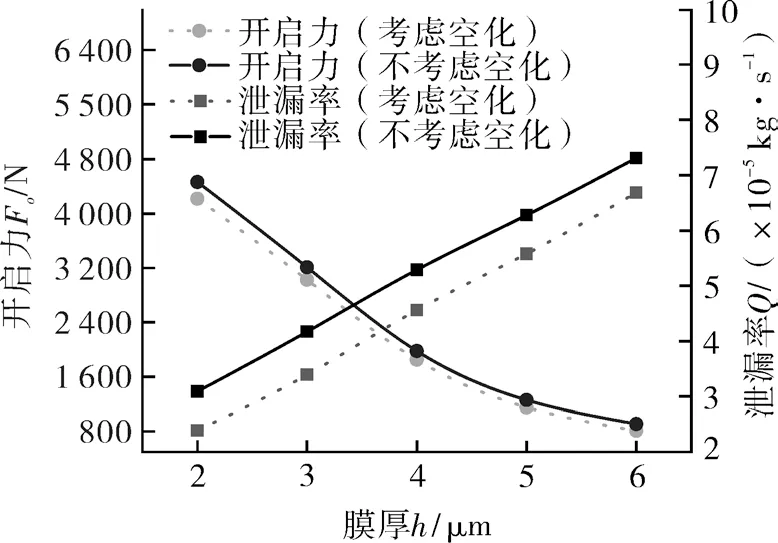
图13 膜厚对各密封性能参数的影响Fig.13 Effect of film thickness on each sealing performance parameter

4 结论

（1）考虑空化效应的开启力和泄漏率均小于不考虑空化效应的值，且较高转速、较低密封压力更易促进液膜的空化。

（2）螺旋槽的泵送能力和流体动压效应均随着槽深、膜厚和螺旋角的增大先增强后持续减弱。考虑空化效应时槽根部的最大压力大于不考虑空化效应时的值，密封稳定性较差。综合考虑其密封性能，当槽深10～14 µm、膜厚3～4 µm、螺旋角15°～20°时整体密封性能最好。

（3）虽然空化效应使密封开启力减小，但却大大降低了泄漏率，因此在今后的工程设计和应用中应该充分考虑空化效应对密封性能的影响。