轻量化搅拌摩擦连接设备横梁的多目标优化设计

曹可可，汪洪峰.，朱增宝，宋娓娓

（1.安徽理工大学 机械工程学院，安徽 淮南 232001；2.黄山学院 机电工程学院，安徽 黄山 245041）

搅拌摩擦连接（Friction Stir Joining,FSJ）具有无烟尘、变形小、接头力学性能好等优点，广泛应用于航空航天、轻轨、汽车和列车等领域，该技术1991年由英国焊接研究所（The Welding Institute,TWI）发明[1-3]。在搅拌摩擦连接过程中由于需要很大的下压力，为保证设备的动刚度和稳定性，现有的搅拌摩擦连接设备多为大型机械，这些设备不仅结构复杂、质量重、体积大，而且价格非常昂贵[4,5]。随着现代工业技术的迅速发展，无人机、高铁、轻轨、火箭的制造数量不断增加，为了节能和降低成本，设计制造中结构的轻量化越来越重要。在保证结构性能安全的前提下减少材料的厚度[6]，如无人机、轻轨、火箭等内部装置及外壳，对于这些厚度小于1mm 的薄板铝合金的加工，使用大型搅拌摩擦连接设备很不方便，而且大部分设备可加工厚度为1mm以上的板材[7]，因此本文针对1mm以下薄板的连接，设计了一台轻量化搅拌摩擦连接设备。

搅拌摩擦连接设备的横梁作为主轴的支撑结构，其静动态特性对设备的性能影响非常大，而设备的性能又直接影响加工产品的质量[8]。因此横梁具有良好的性能是满足高精、高速加工的技术的要求，目前已有很多学者对横梁的结构优化设计进行研究。朱金波等[9]通过模态分析及拓扑优化方法，将质量、总变形量和1阶频率作为优化目标，横梁筋板厚度与位置作为设计变量，优化设计分析后使横梁整体结构性能得到提高；任工昌等[10]以横梁固有频率和质量为优化目标，通过灵敏度分析选出3个尺寸为设计变量，通过中心组合设计试验方法进行优化设计，提高了铣床的加工精度；胡世军等[11]利用拓扑优化方法和筋板类型比对分析对横梁进行轻量化设计，得到最优的横梁优化结构，从而提高了整机的动态性能。

本文以设计的轻量化搅拌摩擦连接设备横梁为研究对象，对横梁设计的合理性与正确性进行分析验证，并采用灵敏度分析和最佳填充空间设计相结合的方法，将横梁的重量、整体变形、模态分析的1 阶频率为目标对其进行优化，优化结果使横梁在满足安全性能的条件下将质量减少最大，以符合轻量化设计要求。

1 横梁静动态分析与优化目标确定

1.1 横梁模型建立

搅拌摩擦连接设备主要由横梁、立柱、底座、主轴、工作台等部分组成。如图1(a)所示为设计的轻量化搅拌摩擦连接设备的三维模型。横梁结构两端固定在立柱上，主轴的重力及工作时的负载直接作用于横梁上，因此在搅拌摩擦连接时，横梁更容易发生较大变形和与主轴电机共振情况。横梁结构三维模型如图1(b)所示，横梁的相关参数如表1所示。

图1 微型高速搅拌摩擦连接设备与横梁结构模型

表1 横梁相关参数

1.2 横梁有限元模型建立

设计的横梁内部是纵横交错的筋结构，因此利用Ansys Workbench软件的壳体单元对横梁结构进行网格划分。为了便于有限元分析，忽略螺纹孔、倒角等微小特征将模型简化。

横梁的自重利用软件加载载荷Standard Earth Gravity 模块设置。工作时最大负载为1000N，作用在主轴与横梁中间位置（变形最大）的连接面上[8]，主轴的自重通过施加竖直向下570N 的远端力来模拟，远端距离为150mm，如图2所示。

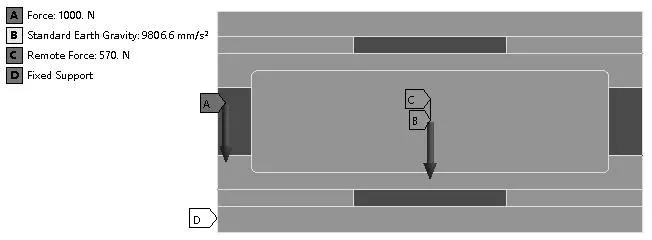
图2 力加载简化模型

1.3 静力学特性结果分析

横梁结构的静力学分析结果如图3 所示，由图可知，在接近现实工况下，整体变形发生在横梁中间位置，大小为1.428μm。受到最大应力为1.132Mpa，而材料的屈服强度为355Mpa，所以横梁的结构设计比较保守，可以进一步优化。

图3 横梁结构变形云图和应力云图

1.4 横梁结构模态分析

根据振动理论原理可知，影响设备结构振动特性较大的是设备的低阶固有频率，因此基于静力学分析模型，对横梁1-6阶模态进行分析，振型云图如图4所示，频率及振动特点如表2所示。

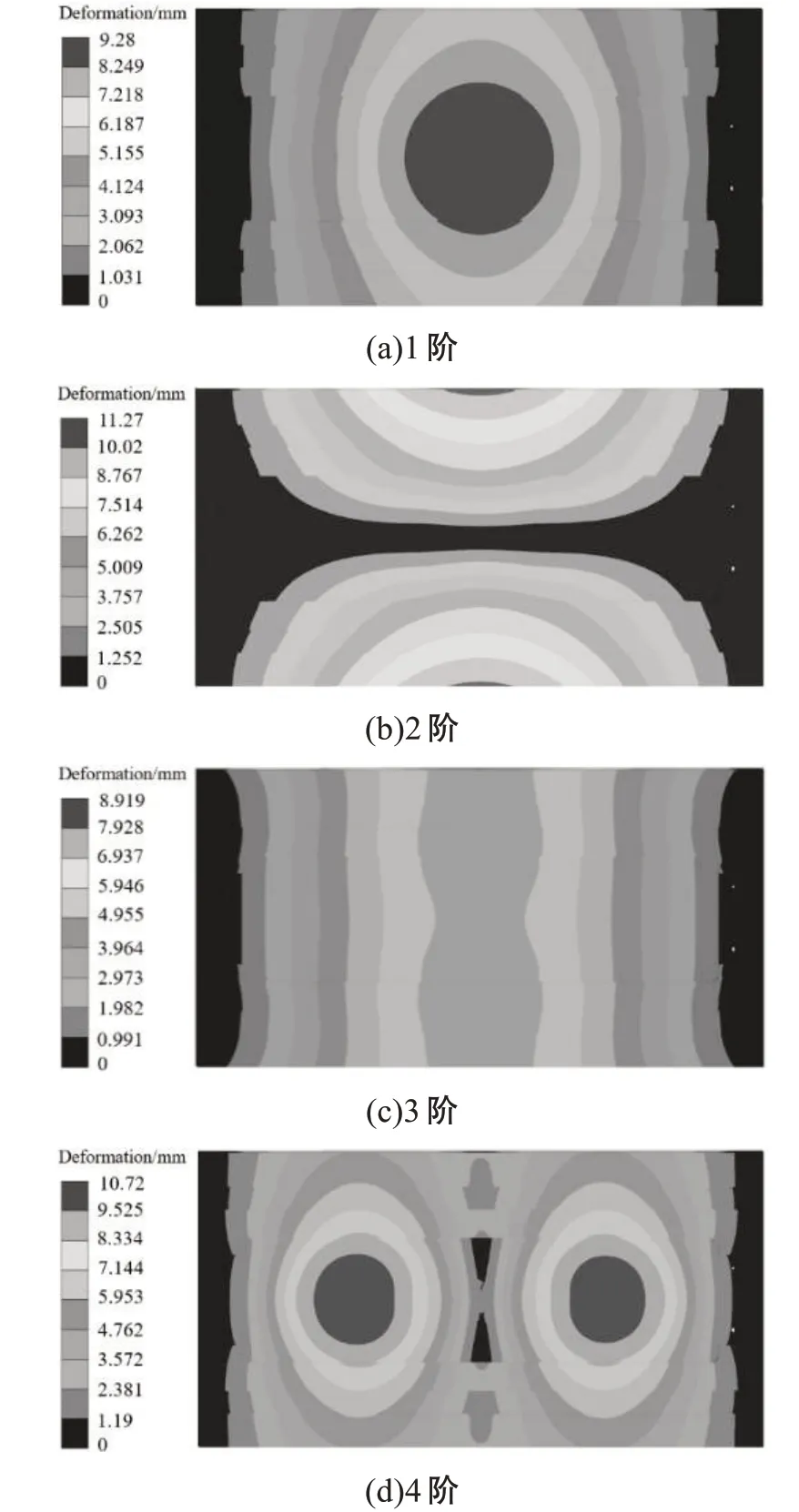
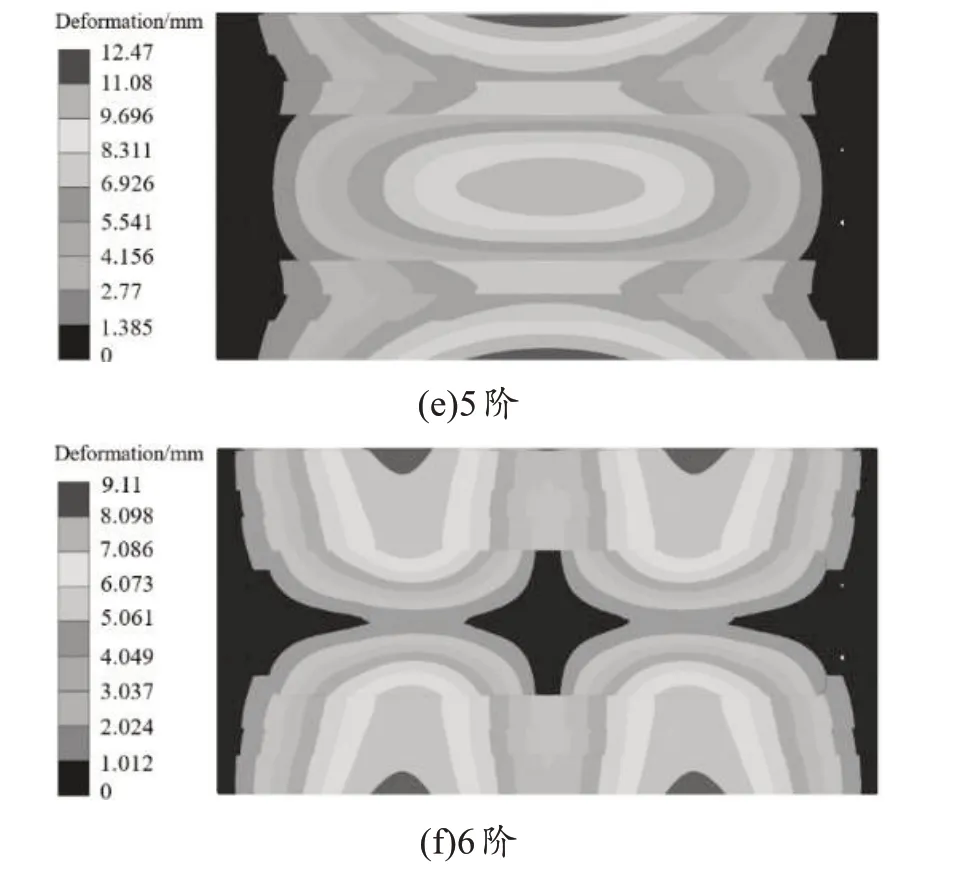
图4 横梁结构前6阶模态振型云图

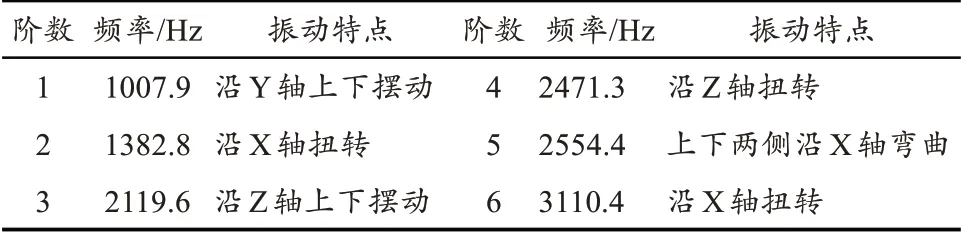
表2 横梁结构前6阶模态固有频率及振型特点

当电主轴高速运转时会对横梁产生激振作用，电主轴对横梁激振频率的计算公式[8]为：

其中：n 为电机工作时最高转速，f 为电主轴对横梁的激振频率，δ为常数，一般取50。

电机运转时最大速度可达24000r/min，代入（1）式得f 为801.67Hz，小于横梁1 阶固有频率，因此横梁与电机不会产生共振。

2 横梁结构的多目标优化设计

2.1 灵敏度分析

由于横梁结构比较复杂，尺寸参数较多，为了选取对横梁性能影响较大的有效参数，选择7 个参数尺寸对其进行灵敏度分析，初始参数及变化范围如表3所示，分析结果如图5所示。

表3 横梁结果设计参数尺寸变化范围

由图5 可知，P1、P2、P4、P6 对质量影响较明显；P2、P4、P6 对整体变形影响较明显；P2、P4 对频率的影响较明显，因此取P1、P2、P4、P6 作为设计变量对横梁进行优化。

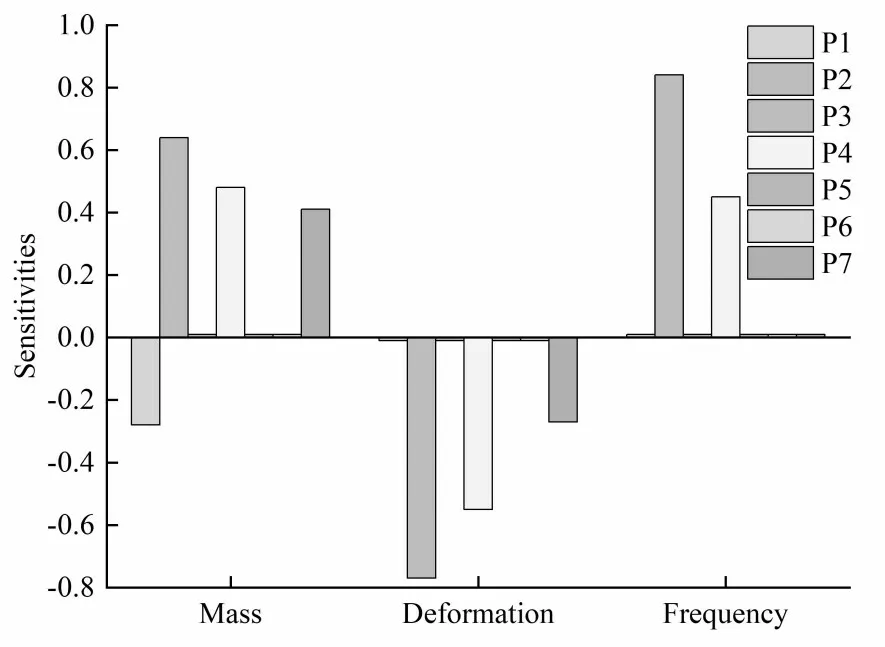
图5 横梁各尺寸灵敏度分析结果

2.2 试验设计及响应面模型构建

为了创建准确的响应面，利用最佳填充空间（Optimal Space Filling，OSF）设计方法在设计变量可行域内取得一定数量的样本点。以P1、P2、P4、P6为设计变量，重量、整体变形和1 阶频率为目标函数，设置100 个样本点，基于响应面全2 阶多项式算法建立响应面模型，响应面拟合曲线如图6所示，由图可知设计点与响应面匹配度较好。

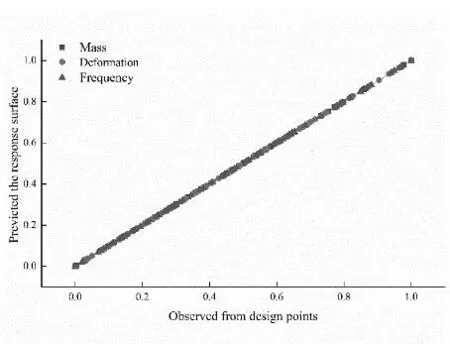
图6 响应面拟合优度曲线

如图7所示为设计变量对目标函数影响关系的响应面。通过响应面分析可知，各设计变量与质量呈线性关系，与整体变形及频率呈非线性关系。

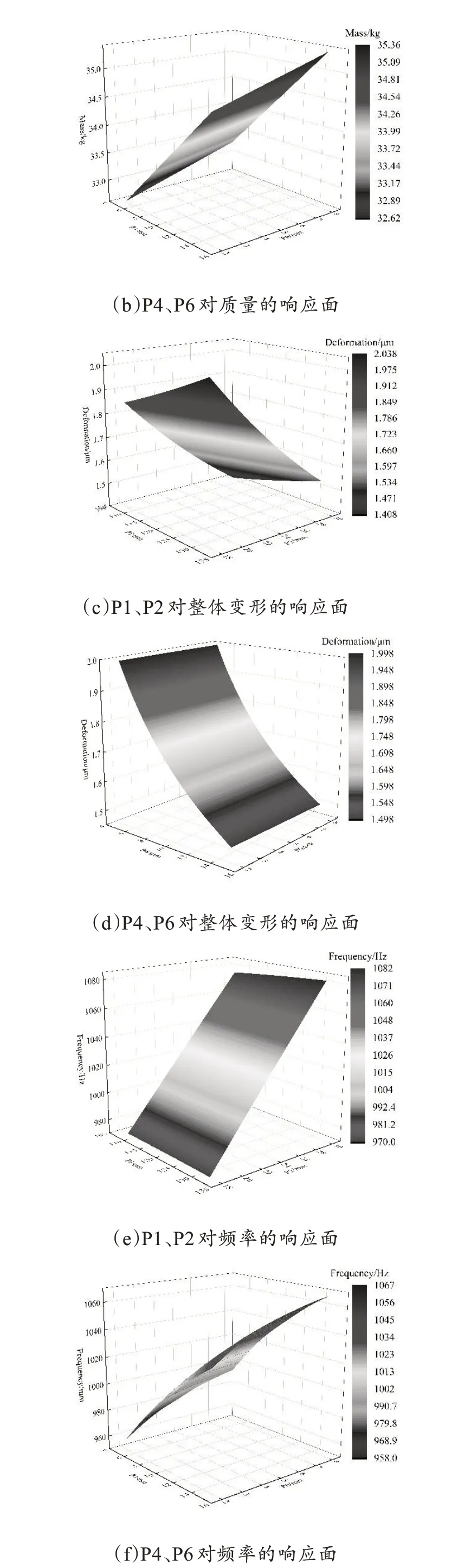
图7 设计变量对横梁性能的响应面

2.3 多目标优化

由静动态特性分析可知，横梁的设计比较保守，所以对结构进行优化时，在保证等效应力、变形量及1阶固有频率在安全范围内同时实现结构的轻量化，建立结构优化数学模型如下：

利用Response Surface Optimization 模块以横梁重量最小，频率最大以及整体变形最小为目标函数进行优化，得到3组最优解，如表4所示。

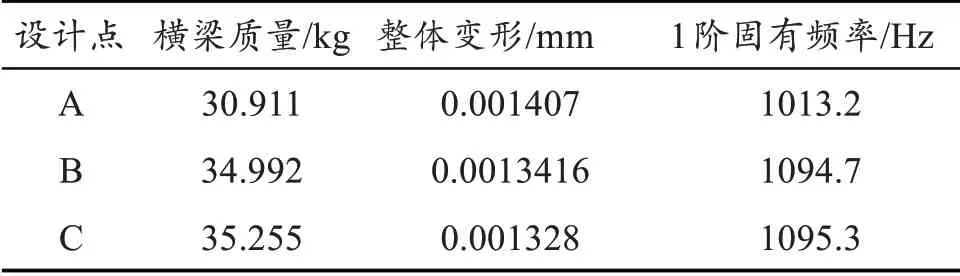
表4 横梁优化结果

3 优化结果分析验证

对表4 横梁的优化结果分析可知，C 设计点整体变形最小、频率最大，但在不影响设备性能的情况下，为体现绿色制造理念，应优先考虑横梁的轻量化设计。所以综合考虑，选取A点进行设计。

对优化结果重新进行静动态分析，结果如图8所示，表5为优化前后结果对比。

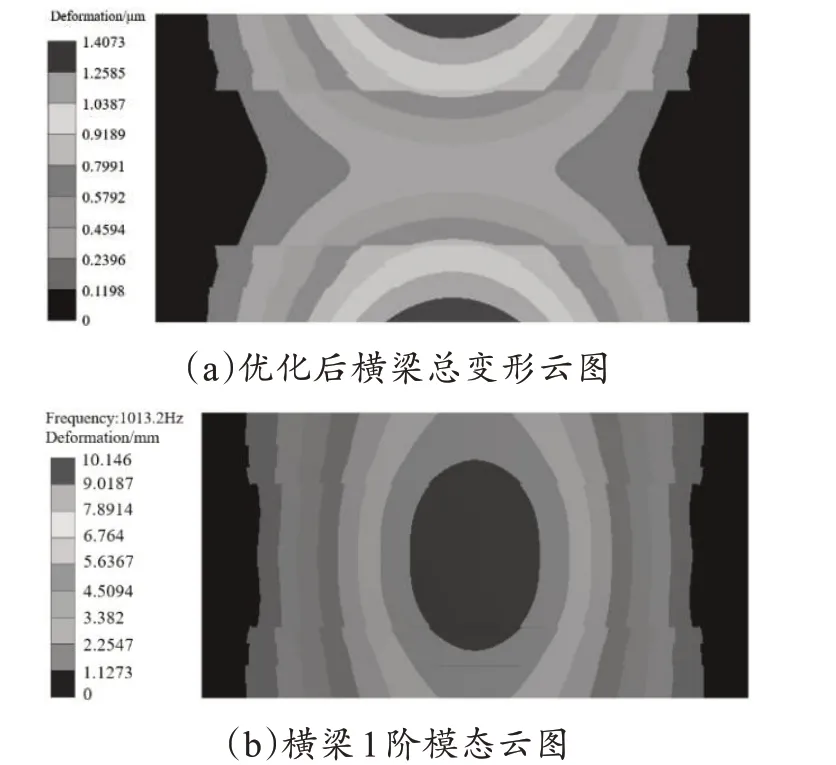
图8 变形云图与1阶模态云图

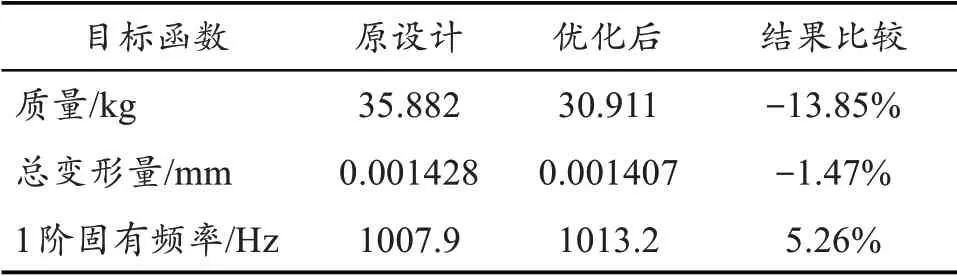
表5 横梁优化前后结果对比

4 结 论

根据对横梁结构静动态特性分析结果，验证了横梁设计的正确性，同时提出基于灵敏度分析和OSF 设计的方法对横梁进行优化设计，结果表明：横梁优化后整体变形减少了1.47%，1阶频率增加了5.26%，提高了横梁的静动态性能，在此基础上横梁的质量减少到30.911kg，满足在保证安全性能的情况下，有效地减少了横梁的质量，符合现代机械设备绿色制造和设备轻量化设计的要求。