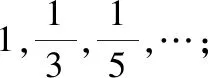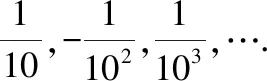数列通项公式的唯一性之规范探究

◎刘子辉

(盐城幼儿师范高等专科学校，江苏 盐城 224000)

课堂教学是师生之间、生生之间交往互动和共同发展的过程课堂教学中，我们经常碰到各种各样的问题，这些问题往往可以作为教研资源一名教师，特别是青年教师，必须牢固树立问题意识，善于用审慎的目光观察各种教学现象，养成收集、整理、分析、钻研这些教学现象的习惯，不断提高自己发现问题、提出问题、分析问题、解决问题的能力，从而提升自己的专业知识水平下面，笔者以数列教学为例，针对教材、教辅和学生作业中经常出现的一些似是而非的表述，阐述一下笔者分析、思考的过程，以求教于读者

一、发现问题

(一)背景材料

在一些教材、教辅及学生的作业中，我们经常可以看到下面的表述：

写出数列的一个通项公式，使它的前4项分别是2，4，6，8

此数列的前4项2，4，6，8都是项数的2倍，所以它的通项公式是=2

一些练习册和校内考试的试卷中，经常出现下面的说法：

数列1，3，5，7，…的通项公式是

(二)发现问题

对于教材、教辅和学生作业中的这些常见表述，许多教师已司空见惯其实，作为教师，特别是数学教师，其思维应该是严密的、合乎逻辑的仔细分析材料就会发现，从逻辑上讲，上面的表述并不是完全一致的

材料一的题目中，要求写出的是已知数列的“一个”通项公式，而材料一的解题过程中，通项公式的前面没有写出定语“一个”“一个”没有写出来，这重要吗？有没有影响呢？如果无关紧要，当然可以不写；如果不能不写，当然应该写出来强调一下！材料二的题目中没有出现“一个”二字，这样表述可以吗？到底对不对呢？显而易见，上面两种情况，说的是一回事，道理是一样的

数学是思维的体操教师应该充分利用上面这些教学资源深入思考，同时有效引导学生深入研究，培养他们的思维能力反之，在数学教学中，如果我们习惯了或认可了上面的说法，时间长了，部分教师和学生便会形成这样的认识：不管是什么样的数列，只要给出了它的前几项，它的通项公式都是唯一的因此，我们有必要对上面的问题做进一步探讨

二、提出问题

深入思考可以发现，上面的问题与下面两个问题本质上是一致的我们先来看日常生活中的例子：

滨江市第一高中只有一位正职校长，叫秦达；有三位副校长，分别是张三、李四和王五那么，我们既可以说秦达是滨江市第一高中校长，也可以说滨江市第一高中校长是秦达我们可以说张三是滨江市第一高中副校长，但不能说滨江市第一高中副校长是张三所以，不考虑逻辑，随便说话，就容易犯错

数学中类似的例子很多，比如“自然数的单位”这个问题以下面两道判断题为例，很多人在做这两道题时，往往会掉入陷阱

(1)自然数的单位是1

( )

(2)1是自然数的单位

( )

第(1)题，“自然数的单位是1”这道判断题是错的，因为，自然数的单位不是唯一的，有个(一)，十，百，千，万，十万，百万，千万，亿，…，所以我们可以说：

个(一)是自然数的单位，

十是自然数的单位，

一百是自然数的单位，

一千是自然数的单位

……

但是不能说：

自然数的单位是个(一)，

自然数的单位是十，

自然数的单位是一百，

自然数的单位是一千

于是，上面的第(2)题“1是自然数的单位”是正确的

从数学的角度看，虽然自然数的单位有很多，但是自然数的基本单位只有一个，那就是“1”所以，我们既可以说自然数的基本单位是1，也可以说1是自然数的基本单位

由此看来，给定数列的前几项，如果根据这个数列前几项的排列规律，只能唯一地写出这个数列的以后各项，那么背景材料一的解题过程和背景材料二的题目中的“一个”就显得不重要了，“一个”既可以写，也可以不写如果根据一个数列的前几项，写出的数列的以后各项不是唯一的，那么，前文所述的背景材料一的解题过程和背景材料二的题目中，“一个”就不能不写了

于是，我们要研究的问题就变成：给定数列的前几项，根据这个数列前几项的排列规律写出的这个数列的以后各项是否唯一

三、分析问题

因为数列的项形形色色，数列的个数有无穷多个，所以要直接回答“给定数列的前几项，根据这个数列前几项的排列规律写出的这个数列的以后各项是否唯一”这个问题，就显得十分困难需要从具体例子入手展开研究

看到这里，读者心里肯定会想：那么结论到底是什么？下面，我们就以数列2，4，8，…的通项公式为例进行研究

对于数列2，4，8，…，绝大多数同学会很快求得它的通项公式为=2

理由：因为=2,=4,=8，

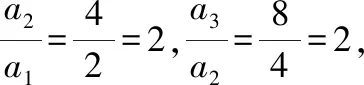
所以这个数列是等比数列，且公比=2由等比数列的通项公式得

=·-1=2×2-1=2

从而得出数列2，4，8，…的通项公式是=2的结论

我们的结论是数列2，4，8,…的通项公式不是唯一的，=2只是它的一个通项公式，而它的通项公式还可以有其他形式

由此可见，背景材料一中，例题的说法没有问题，问题在于，它的解题过程中漏掉了“一个”二字正确的解题过程如下：

此数列的前4项2，4，6，8都是项数的2倍，所以它的一个通项公式是=2

同样，背景材料二的题目中，问题也是漏掉了“一个”二字题目应该改为数列1，3，5，7，…的一个通项公式是

四、解决问题

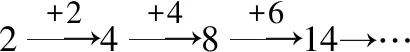
数列,,,,…,…从第二项起，每一项与它的前一项的差按前后次序，排成了一个新数列-,-,-…,+1-,…

前面那个新数列2，4，6，…可以看成一个公差为2的等差数列显然，数列,,,,…,…与等差数列有一定的“血缘关系”，数列理论中把这样的数列称为二阶等差数列为区别于二阶等差数列，我们把通常定义的等差数列称为一阶等差数列那么二阶等差数列的通项公式如何求呢？我们可以采用求等差数列通项公式的思路解决此问题

设数列,,，…,,…是一个二阶等差数列，为了书写的方便，我们把数列-,-,-，…,+1-,…简记为

,,,…,,…

(1)

则数列(1)为等差数列，且有=+1-(≥1,∈)

设数列(1)的公差为，则

=-=-=…=+1-(≥1,∈)，

因此，=-=(-)-(-)=-2+

由于=+(-1)，

∴+1-=+(-1)，

即+1=++(-1)

依此规律，则有

=+，

=++，

=++2，

……

=-1++(-2)

把上面各式左右分别相加，得

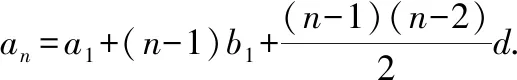
这就是二阶等差数列的通项公式，其中，=-，

=-2+

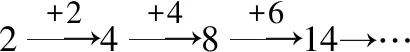
我们来检验一下其正确性：

当=1时，=1-1+2=2；

当=2时，=2-2+2=4；

当=3时，=3-3+2=8；

当=4时，=4-4+2=14

完全正确！

这样，上面得到的结论又进一步验证数列2，4，8，…的通项公式不唯一=2是它的一个通项公式，此时，=2=16=-+2也是它的一个通项公式，此时=14那么以2，4，8为前3项的数列，通项公式到底有几个呢？2个，3个，……，还是无数个？

要回答这个问题，我们还是用事实加以证明有人说，=-5+10-4也是它的一个通项公式，对不对呢？

我们来代入检验：

当=1时，=1-5×1+10×1-4=2；

当=2时，=2-5×2+10×2-4=4；

当=3时，=3-5×3+10×3-4=8；

所以，=-5+10-4确实是数列2，4，8，…的一个通项公式，只不过这时=4-5×4+10×4-4=20(注意，这时通项公式是的3次方的形式，原数列已经变成三阶等差数列了)

综上所述，我们不难得出结论：以2，4，8为前3项的数列通项公式不唯一如果把=2当作一个通项公式，第4项就是16；如果把=-+2当作一个通项公式，第4项就是14；如果把=-5+10-4当作一个通项公式，第4项就是20通项公式不同，第4项也不同如果我们大胆假设第4项为任意给定的一个实数，是否能得到这个数列的一个通项公式呢？因为2，4，8，是4个已知数，我们不妨把通项公式设成4个参数的形式

已知数列为2，4，8，，…

设它的一个通项公式为=+++

其中，,,,为待定系数把=1,2,3,4代入，得方程组如下：

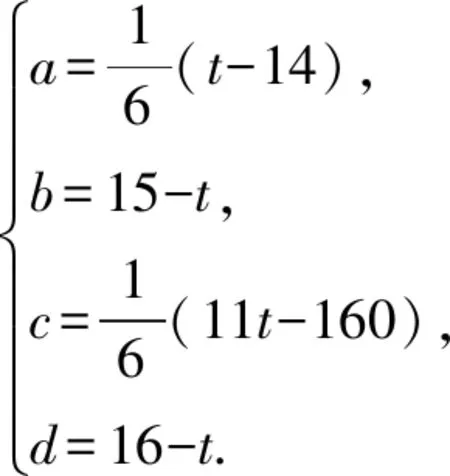
这样，每给出一个值，就可以求得相应的,,,，从而得到所给数列的一个通项公式

事实上，=14时，=0,=1,=-1,=2，这正是前面的通项公式=-+2；当=20时，=1,=-5,=10,=-4，这正是前面的通项公式=-5+10-4

由于可以取任意实数，这样就有无穷多组,,,的值满足条件，所以，以2，4，8为前3项的数列的通项公式有无穷多个每给定第4项的一个值，就可以得到一个通项公式不过，这里得到的无穷多个通项公式，都是用项数的三次多项式表示的，并不包括用其他形式(如用指数形式2)表示的通项公式因此，要写全所有的通项公式是办不到的可见，无论是出题还是解题，“一个”二字千万不能漏写

五、总结反思

一般而言，使用省略号时应明确所省略的各项是按照什么规律排列的这里只给出数列的前三项，而没有明确其后面省略的各项，即没有说明从第四项起以后的各项所遵循的规律，由于第四项的不同，可以得到无穷多个满足前三项要求的通项公式同样，第四项相同而没有明确用什么规律来确定第五项，还是可以得到无穷多个通项公式以此类推，我们可以得出一个共同的结论：只给出前若干项的数列，总可以得到无穷多个通项公式

在教学实践中，我们应该形成这样一种共识：如果出题者的意图是求等比数列的通项公式，那么应当在题目中加上“等比数列”这一条件，即题目应改为“已知等比数列2，4，8，…，求这个数列的通项公式”这时省略号所省略的各项，可按等比数列的规律逐一写出，它的通项公式就是=2

同样道理，求数列1，3，5，…的通项公式，省略掉的规律也不具体，因此也有无穷多个满足前三个条件的通项公式，如=-6+13-7就是其中之一如果题目是考查求等差数列的通项公式，那么应加上“等差数列”这一条件

对于自然数列，应写成自然数列1，2，3，…

有些数列没有特殊的名称，那么应写出它的通项(也就是一般项)以表示所省略的各项的规律例如：

1·2,2·4,3·8,…,·2,…;

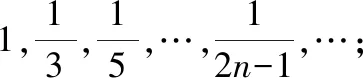
1·2·3，2·3·9，3·4·27，…，·(+1)·3,…

当然，一些教科书考查的是学生通过观察来发现由所给数列的前几项找出熟知的规律，从而能依次写出以后的各项，进而写出它的通项公式的能力，如：

2,4,8,…;