数学史融入数学教学的教学案例探究——基本不等式的证明教学案例

◎张 薇

(江苏省奔牛高级中学，江苏 常州 213131)

一、背景描述

《普通高中数学课程标准(2017年版)》指出：新课程的目标之一为通过高中数学课程的学习，学生能提高学习数学的兴趣，增强学好数学的信心，养成良好的数学学习习惯，发展自主学习的能力；树立敢于质疑、善于思考、严谨求实的科学精神；不断提高实践能力，提升创新意识；认识数学的科学价值、应用价值、文化价值和审美价值课程的设计依据数学学科特点，关注数学逻辑体系、内容主线、知识之间的关联，重视数学实践和数学文化数学文化是指数学的思想、精神、语言、方法、观点，以及它们的形成和发展，还包括数学在人类生活、科学技术、社会发展中的贡献和意义，以及与数学相关的人文活动，而数学的价值与数学文化密切相关

英国数学史学家福韦尔认为数学史让学生认识数学文化的多元性，提供了社会和文化因素决定数学发展的例子，他总结了数学教学中运用数学史的15条理由：(1)增加学生的学习动机；(2)改变学生的数学观；(3)因为知道并非只有他们自己有困难，因而得到安慰；(4)使数学不那么可怕；(5)有助于保持对数学的兴趣；(6)给予数学人文的一面；(7)有助于解释数学在社会中的作用；(8)有助于发展多元文化进路；(9)历史发展有助于安排课程内容顺序；(10)告诉学生概念如何发展，有助于他们对概念的理解；(11)通过古今方法的对比，确立现代方法的价值；(12)提供探究的机会；(13)过去的发展障碍有助于解释今天学生的学习困难；(14)培养优秀生的远见卓识；(15)提供跨学科合作的机会由此可见，数学史在数学教育中有重要作用

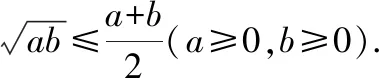
以下给出“基本不等式”一节在四版教科书中的位置、呈现方式以及前后知识顺序

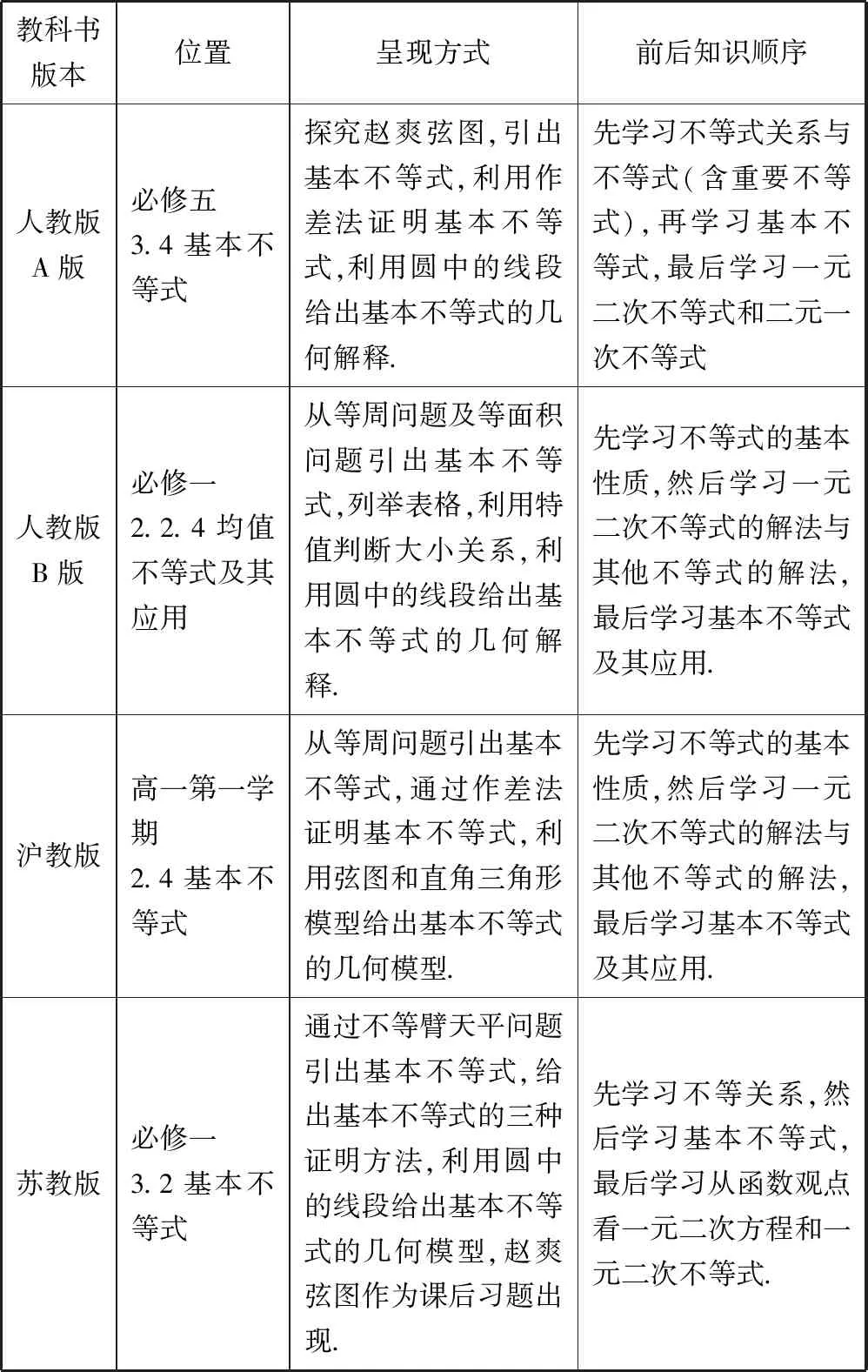
教科书版本位置呈现方式前后知识顺序人教版A版必修五3.4基本不等式探究赵爽弦图,引出基本不等式,利用作差法证明基本不等式,利用圆中的线段给出基本不等式的几何解释.先学习不等式关系与不等式(含重要不等式),再学习基本不等式,最后学习一元二次不等式和二元一次不等式人教版B版必修一2.2.4均值不等式及其应用从等周问题及等面积问题引出基本不等式,列举表格,利用特值判断大小关系,利用圆中的线段给出基本不等式的几何解释.先学习不等式的基本性质,然后学习一元二次不等式的解法与其他不等式的解法,最后学习基本不等式及其应用.沪教版高一第一学期2.4基本不等式从等周问题引出基本不等式,通过作差法证明基本不等式,利用弦图和直角三角形模型给出基本不等式的几何模型.先学习不等式的基本性质,然后学习一元二次不等式的解法与其他不等式的解法,最后学习基本不等式及其应用.苏教版必修一3.2基本不等式通过不等臂天平问题引出基本不等式,给出基本不等式的三种证明方法,利用圆中的线段给出基本不等式的几何模型,赵爽弦图作为课后习题出现.先学习不等关系,然后学习基本不等式,最后学习从函数观点看一元二次方程和一元二次不等式.

在呈现方式上，四版教科书分别从赵爽弦图、等周问题、等周问题、不等臂天平问题引出基本不等式，在顺序上都是先学习不等关系再学习基本不等式

二、案例展示

以下就“基本不等式的证明”的几种不同教学设计略谈一孔之见

设计一：从不等臂天平引入

1片段1——设置问题情境

【设计意图】给不等臂天平赋予趣味性的背景，激发学生的兴趣，调动学生的积极性，激发学生解决问题的强烈愿望

2片段2——组织探究活动

问题1：用这个不等臂的天平，你能不能求出珠宝的实际质量？

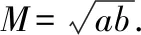
问题2：你是否赞同珠宝商的方案？

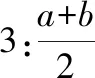
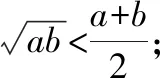
师：非常好！同学们已经走出了得到数学真理的第一步：实验—猜想—归纳数学是一门严谨的科学，我们不能满足于直观获得的结论，而要用严谨的推理来证明这个结论你能给出它的证明吗？

【设计意图】学生从案例出发，有了解决问题的迫切需要

3片段3——展开科学论证

学生独立证明并板书，教师总结

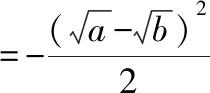
≤0

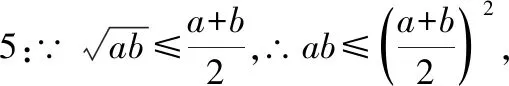
∴4≤+2+，

∴-2+≥0，

即(-)≥0,显然成立

师：观察两位同学的证明过程，说说你的看法

生6：第一种方法是作差比较法，也可以平方以后作差；第二种方法把要证明的结论当条件用了，需要把顺序颠倒一下

∵(-)≥0，∴-2+≥0，

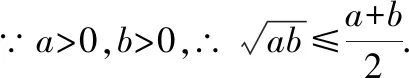
生7：老师，你看这样改可以吗？

因为(-)≥0成立，所以等式成立

师：非常好！虽然第二种方法有点小问题，但是我们稍微改动一下就得到两种不同的方法，其中学生7的方法我们称之为分析法，学生6的方法我们称之为综合法我们发现学生6的方法并不是一眼就能看出来的，而是建立在先对题目进行分析，也就是分析法的基础上书写的所以，一般我们可以先用分析法进行分析，再用综合法证明看来珠宝商还是多赚钱的，只有=时他才是一个守法的商人啊!

【设计意图】本环节请同学板演，选一位从结论开始证明的同学，在同学们的分析中发现问题，经过自己的思考得到正确的结果学生经历了猜想—尝试—修正—得到结论的过程，收获了成功的喜悦，对问题有了更深层次的理解

这是学生进行的一次深度学习，经历了一次从旧知到新知的过程学生对自己猜想的结果进行证明，获得了新的知识，激发了学习数学的兴趣，完成了一次科学探究的过程：“提出问题”—“猜想与假设”—“实验和论证”

问题4：对于基本不等式，你有哪些认识？

生8：不等式左边是积的形式，右边是和的形式

生9：要注意不等式成立的前提条件是非负数，等号成立的条件是两式相等

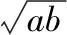
几何直观能启迪思路、帮助理解，因此，借助几何直观学习和理解数学是数学学习中的重要方面，只有做到了直观上的理解才是真正的理解

【设计意图】通过对基本不等式结构的再分析，使学生对基本不等式有更深层次的理解

设计二：从赵爽弦图引入，设置问题情境

师：同学们，请欣赏一下赵爽弦图赵爽，又名婴，字君卿，东汉末至三国时代吴国人,是我国历史上著名的数学家与天文学家，代表作品《勾股圆方图注》

问题1：你能在这个图中找到一些相等关系和不等关系吗？

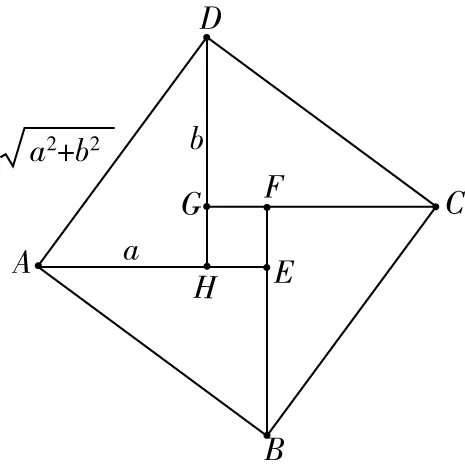
图1

生1：四个直角三角形全等，对应的边角都是相等的

生2：直角三角形的直角边小于斜边，小正方形的边长小于直角三角形的边长

师：研究一个图形，除了研究边角关系外，还研究它的周长与面积从这个方面看，你还能得到哪些不等关系？

生3：每个三角形的面积小于大正方形的面积

生4：四个三角形的面积之和小于大正方形的面积

问题2：正方形中有4个全等的直角三角形，设直角三角形的直角边分别为,，你能用数学符号来表示这个结论吗？

生5：2<+(>0,>0)

师：该不等式能否成为等式？,的范围能否扩大？

生6：当直角三角形变为等腰直角三角形即=时，2=+(∈,∈)

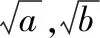
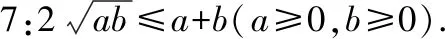
师：这就是我们今天要学习的基本不等式

下同设计一

【设计意图】通过赵爽弦图研究面积关系，引入重要不等式与基本不等式学生通过赵爽弦图了解数学家赵爽，燃起了强烈的民族自豪感

设计三：从等周问题引入，设置问题情境

师：海岛很大，古人既没有航拍图，也无法测算精确的岛屿面积，他们是怎么确定面积的呢？公元前5世纪，雅典人修昔底德测量西西里岛大小的时候，乘船绕海岸线一周，记录航行时间在修昔底德看来，绕岛一周所花费的时间越长，海岸线越长，也就说明该岛的面积越大同学们，你们觉得这个方法有数学依据吗？

生1：有数学依据绕岛时间越长，说明海岸线越长，意味着岛越大

师：公元前2世纪，历史学家波利比乌斯曾说，有人对于等诸城的两个营地可以容纳不同数量的人感到困惑不解.公元1世纪，博物学家老普林尼根据周长来估算不同地区的面积.公元5世纪，古希腊哲学家普罗克拉斯提到，在他所生活的时代，在某些公有制社会里，有人将周长更大但面积更小的土地分配给别人，而把周长更小面积更大的土地分给自己，还被视为大公无私那么，海岸线越长，就意味着岛越大吗？

生2：不一定一个图形周长确定的时候，面积不能确定

师：测量的时候还遇到一个问题：有两座岛周长相等，那么哪个面积大呢？聪明的你怎么解决这个问题呢？

生3：我们将海岛想象成矩形就可以做了

师：非常好的思路，为了让这个问题更利于我们现在解读，可以简化，假设两个图形都是矩形

问题1：你能证明“在周长为定值的所有矩形中，面积最大的是正方形吗”？

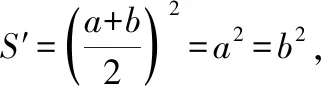
下同设计一

【设计意图】从数学史上的等周问题入手引入基本不等式，学生经历了一次生活—数学—生活的学习过程，把握了问题的本质，化繁为简，通过联想已有的学习经验，运用现有知识解决问题，并由此建构了新知识，成为教学活动的主体在这样的深度教学下，学生发现高级知识都可以由低级知识而来，激发学生学好数学的自信

三、稚化点评

课堂是教师、学生、教材三要素相互碰撞的场所，最大限度地调动学生的学习积极性、充分发挥学生的主体地位、让学生深度学习是数学课堂教学的重要任务因此，创设一个好的课堂情境是数学教学中的一个重要环节“基本不等式”是一节典型的新授课，有很多的情境引入方式

设计一从学生感兴趣的实际问题出发，对书中的情境进行改编，使之更有趣味性，从学生原有的知识和经验中寻找新知识的生长点，与物理知识的结合更是拓展了学生的思维

设计二从赵爽弦图入手，问题的设置引发学生积极思考，在追寻先人的脚步中获得成功的喜悦

设计三从等周问题入手，对书中比较简单的情境引入进行史料的丰富，激发学生的学习动机和解决问题的愿望

笔者所在的教研组对“基本不等式的证明”进行了同题异构，三位教师分别采用了设计一、二、三进行课堂教学从三节不同的课例实践来看，设计三的学生上课反映及接受程度更好除了外在的一些原因，如学生本身的水平及执教教师问题的设置，更多在于情境的设置非常生动有趣，直接将学生代入情境，使学生有了迫切解决问题的愿望在数学教学中融入数学史并不是为历史而历史，而是要使数学史发挥其独特的作用，否则就毫无意义，只会挤占课堂时间任何一个主题的背后都有丰富的史料，但并非所有史料都适合课堂教学，这就需要执教教师大量阅读，有丰富的知识积累，化繁为简，设计适合学情的情境，让学生在数学知识学习中提高数学素养，在深度学习中发展兴趣、培养自信、获得成功

将数学史融入数学教学过程，教师会遇到很多困难，如资料欠缺、学生无基础等，但要明白在教学中融入数学史的价值与重要性，只有提高自己的数学史积累才能做到融会贯通、引入自然、润物细无声