新高考背景下的一个高中数学教学案例——抛物线的简单几何性质(第一课时)

◎丛文娟

(新安中学集团高中部,广东 深圳 518101)

一、引 言

新高考背景下，知识的传授不应当局限于知识本身，应当在教学过程中，始终以提高学生能力和素养为目标本节教学设计中，数形结合的思想贯穿始终，让学生从“形”的角度直观感受，从“数”的角度进行验证，有助于提高学生的逻辑推理能力、直观想象能力、数学运算能力等核心素养

二、教学目标

1掌握抛物线的简单几何性质：范围、对称性、顶点、离心率

2能根据抛物线的几何性质对抛物线方程进行讨论

3对通径、焦半径公式进行初步探索

4进一步理解数形结合思想在解析几何中的应用

三、教学重难点

1教学重点：抛物线的简单几何性质、利用抛物线的几何性质求方程、对通径与焦半径公式的初步探究

2教学难点：利用数形结合思想对通径、焦半径公式进行探究

四、教学过程

1利用数形结合思想探究抛物线的简单几何性质

11 知识回顾，温故知新

【学生活动】学生完成学案内容，对抛物线的四种方程、图形、焦点坐标、准线方程等进行复习

图形方程y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)焦点p2,0()-p2,0()0,p2()0,-p2()准线x=-p2x=p2y=-p2y=p2

【设计意图】之前学过椭圆、双曲线的几何性质，都是通过图形和方程两方面进行研究的，因此引导学生对抛物线的四种方程、图形、焦点坐标、准线方程进行复习，有利于进一步探索抛物线的性质

12 数形结合，类比探究

1类比用标准方程研究椭圆、双曲线几何性质的过程与方法，思考：我们要研究抛物线的哪些几何性质？如何研究这些性质？

前面学习了椭圆、双曲线的范围、对称性、顶点和离心率，在双曲线中还学习了渐近线，我们是通过“数”和“形”两方面对椭圆、双曲线的几何性质进行探究的

【设计意图】类比椭圆、双曲线几何性质的研究思路，为接下来用数形结合法研究抛物线的几何性质做铺垫

2观察图1，你能发现抛物线横、纵坐标的取值范围吗？

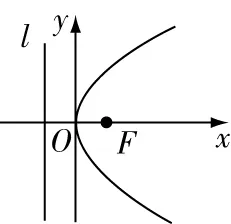
图1

通过观察图形，学生很容易得到开口向右的抛物线的横、纵坐标的取值范围，即为≥0,∈

3从数的角度，也就是从抛物线方程的角度，怎样得到抛物线的横、纵坐标的取值范围呢？

在方程=2,>0中，并无限制，因此∈因为2=≥0，且>0，所以≥0

【设计意图】让学生从“数”和“形”两个角度探索抛物线的取值范围

4观察图2，抛物线有几条对称轴？是否有对称中心？

图2

观察图形，容易发现开口向右的抛物线关于轴对称，没有对称中心

5从“数”的角度，怎样说明抛物线=2,>0的图像关于轴对称？

要说明抛物线的图像关于轴对称，只需要在抛物线上任取一点(,)，说明(,)关于轴的对称点′(,-)也在抛物线上即可

【设计意图】引导学生从“数”和“形”两个角度探索抛物线的对称性

6根据图3，你能写出抛物线的顶点坐标吗？

图3

(0,0)

7从“数”的角度，如何从方程中得到抛物线的顶点？

在抛物线方程中，=2,>0，令=0，得到=0

【设计意图】引导学生从“数”和“形”两个角度探索抛物线的顶点

给出抛物线离心率的定义，并根据抛物线的定义得出离心率为1

此时，继续引导学生复习椭圆和双曲线的定义和取值范围

13 适时归纳，总结提升

①(范围)抛物线只位于半个坐标平面内

②(对称性)抛物线只有1条对称轴,没有对称中心

③(顶点)抛物线只有1个顶点、1个焦点、1条准线

④(离心率)抛物线的离心率是确定值1

2一题多变，一题多解，学以致用

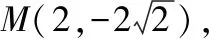
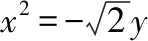
【设计意图】例题1和变式训练都是对抛物线性质的初步应用，进一步强化待定系数法求抛物线方程的训练

2斜率为1的直线经过抛物线=4的焦点，且与抛物线交于,两点，求线段的长

方法1：联立直线和抛物线方程，求出,两点的坐标，利用两点间距离公式求出的长

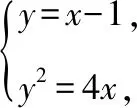
方法2：利用抛物线的定义，将焦点弦的长度转化为两个焦半径的长度,可以利用方法1求出,，也可使用韦达定理

||=||+||=(+1)+(+1)=++2

【设计意图】引导学生多角度思考，培养学生的逻辑思维能力，为接下来探索焦半径和通径公式做铺垫

8连接抛物线上一点与焦点的线段叫作抛物线的焦点弦根据例题2的方法2，你能否得到抛物线的焦点弦公式？

9你能否总结出另外三种抛物线的焦半径公式？

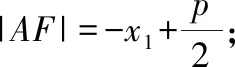
10有一种特殊的焦点弦，它垂直于抛物线的对称轴，这种焦点弦叫作通径你能根据焦半径公式求出通径的长度吗？

通径||=2

【设计意图】引导学生对焦半径公式、通径进行提炼与总结

3深入思考，思维升华

1双曲线的开口大小由离心率来衡量，那么抛物线的开口大小怎样确定呢？

通径越长，开口越大

【设计意图】类比双曲线，引导学生利用通径对抛物线的形状进一步探索

2通径是一类特殊的焦点弦，那么通径是抛物线最短的焦点弦吗？

【设计意图】思考2由特殊抽象到一般，为下一节课进一步探索抛物线的焦点弦问题埋下伏笔在下节课中，将采用更为多样的方法求证“通径就是抛物线最短的焦点弦”

4小组活动，总结提升

【小组活动】小组合作，探究另外三种抛物线的几何性质

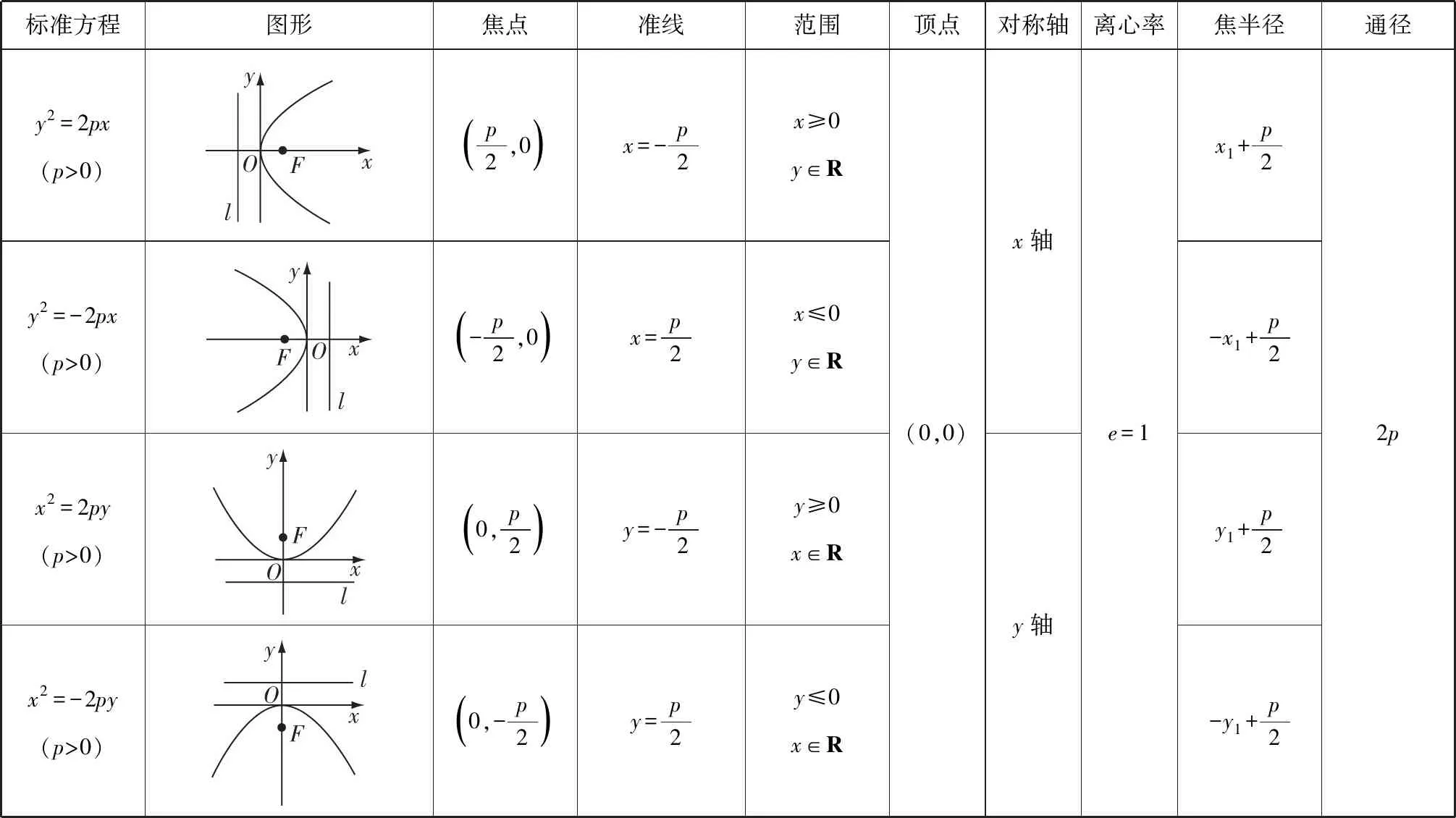
标准方程图形焦点准线范围顶点对称轴离心率焦半径通径y2=2px(p>0)p2,0()x=-p2x≥0y∈Ry2=-2px(p>0)-p2,0()x=p2x≤0y∈Rx2=2py(p>0)0,p2()y=-p2y≥0x∈Rx2=-2py(p>0)0,-p2()y=p2y≤0x∈R(0,0)x轴y轴e=1x1+p2-x1+p2y1+p2-y1+p22p

【设计意图】引导学生利用数形结合思想对其他三种抛物线进行探究

总结课堂内容并提出思考：你还有几种方法说明“通径就是抛物线最短的焦点弦”？

【设计意图】(1)梳理本节内容，提炼方法

(2)为下节课继续探究焦点弦问题埋下伏笔

四、课后作业

(1)《数学选修2-1》第136页课后习题

(2)思考：你还有几种方法说明“通径就是抛物线最短的焦点弦”？

本节课作为一节真实课例(40分钟)，将数形结合思想贯穿始终，采用小组合作探究、问题串等形式，让课堂充满活力，从而提高学生的核心素养课堂最后，“通径是否为抛物线最短的焦点弦”这个问题抛砖引玉，为下节课继续研究抛物线的焦点弦问题埋下伏笔