莫来石纤维增强SiO2气凝胶复合材料压缩回弹性能实验与建模研究
吕双祺,黄 佳,孙燕涛,付尧明,杨晓光,石多奇*
(1 中国民用航空飞行学院 航空工程学院,四川 广汉 618307;2 中南大学 航空航天学院,长沙 410083;3 北京航空工程技术研究中心,北京 100076;4 北京航空航天大学能源与动力工程学院,北京 102206)
气凝胶(aerogel)是一种新型纳米多孔非晶固体材料,具有低密度(0.003 g/cm3)、高孔隙率(99.8%)、大比表面积(1000 m2/g)等特点。由纳米颗粒骨架构成的多孔网络结构(颗粒直径约1~5 nm,孔洞直径约为1~100 nm)十分独特,降低固态热传导并限制内部热对流,使得气凝胶材料拥有优异的隔热性能,是目前公认的热导率最低的固体材料[1-2]。但是,多孔结构使其强度低、脆性大,限制了气凝胶在承载结构或组件中的广泛应用。研究表明,采用添加纤维、颗粒、碳纳米管等增强相的方法来制备气凝胶隔热复合材料,能够在尽可能不影响隔热性能的前提下提高力学性能[3-4]。陶瓷纤维增强气凝胶复合材料不仅具有优异的耐温能力和隔热性能,而且具备相对较高的强度和韧性,因此被推广应用于航空航天、军事装备、工业建筑等领域。在高超声速飞行器热防护领域,将其选用为大面积热防护系统中的承载隔热材料,以提高热防护效率,减轻飞行器质量[5-6]。当飞行器以高超声速再入飞行时,外表面热防护系统不仅需要承受严酷的气动加热以使内部设备维持在允许温度范围内,而且需要承受一定的机械载荷以维持飞行器的气动外形与结构完整。一旦热防护材料及结构因过载、冲击等原因发生破坏或缺失,将会引起防隔热功能的丧失。此外,不可恢复的密实化也会破坏飞行器的气动外形,进而影响飞行效率和气动加热[7-8]。因此,有必要研究热防护材料及结构的力学性能,以促进材料改进、结构设计与强度评估等。国内外研究人员针对此类气凝胶复合材料的力学性能已开展了一系列研究工作。高庆福[9]系统地开展了SiO2,Al2O3等体系陶瓷纤维增强气凝胶复合材料的工艺优化与分析工作,研究溶胶配比、纤维种类和纤维体积分数等对力学性能的影响规律。Hou等[10]采用快速凝胶工艺制备ZrO2纤维增强ZrO2-SiO2气凝胶复合材料,研究纤维体积分数对压缩行为的影响。余煜玺等[11]制备了SiC微/纳纤维毡增强SiO2气凝胶复合材料,测试并分析纵向和横向拉伸性能及导致差异的原因。Shi等[12-13]揭示了陶瓷纤维增强SiO2气凝胶复合材料在不同载荷形式下的力学特性,如各向异性、拉压不对称等。Yang等[14]研究了陶瓷纤维增强碳气凝胶复合材料在准静态和动态压缩载荷下的力学行为及断裂机理,讨论了应变速率带来的影响。为了使飞行器能够维持好一定的气动外形,需保证材料及结构在长时间受载及预期的重复使用条件[15]下仍能维持在一定变形量限制以内,这对于热防护系统的正常工作同样重要。Yang等[16-17]开展了不同温度条件、载荷水平下陶瓷纤维增强气凝胶复合材料的压缩蠕变实验,阐释室温长时/高温短时蠕变行为和形成机制。在目前的研究工作中,较少关注此类承载隔热材料受压卸载后的变形恢复能力[18],甚至是在交变载荷下的变形行为,这又与重复使用密切相关。许多有机体系、有机增强或交联的气凝胶复合材料可以在产生较大宏观变形的情况下表现出很好的弹性恢复能力[19-20],通过合理的多层级微观结构设计及制备得到的陶瓷纳米纤维气凝胶材料可以在1000周次以上循环压缩载荷后仍然保持较好的弹性[21-22]。但是,上述具有较好回弹性能的气凝胶及其复合材料或耐温不足,或模量极低,无法满足热防护领域的实际工程需求。在气凝胶及其复合材料力学建模方面,国内外学者也采用了多种方法开展研究。针对气凝胶基体内的颗粒骨架网络,采用分子动力学模拟的方法建立微观结构与力学性能之间的联系[23]。在稍大尺度上,针对有机交联气凝胶,Roy等[24]采用粗粒度模拟方法模拟压缩、拉伸和弯曲过程。Fu等[25]采用无网格的物质点方法模拟分析材料的动态压缩力学行为。对于纤维增强气凝胶复合材料,Lu等[26]建立基于细观力学分析和有限元方法的多尺度建模方法,并分析纤维特征参数等对性能的影响规律。在宏观尺度上,已初步建立起描述陶瓷纤维增强气凝胶复合材料双模量特性[27]、蠕变行为[16]的本构模型,但对于压缩回弹、循环变形行为的描述尚缺乏相应建模研究工作。
本工作针对陶瓷纤维增强气凝胶复合材料在压缩回弹过程中表现出的变形恢复能力进行实验与建模研究。首先,开展不同极限应变下陶瓷纤维增强气凝胶复合材料的压缩回弹实验,阐释非线性力学行为的成因,对变形恢复能力进行定量评估;其次,研究不同热暴露温度对于压缩回弹行为与变形恢复能力的影响,分析高温热暴露下微观结构发生的变化;最后,建立描述加载和卸载阶段变形行为的唯像力学模型。
1 实验材料与方法
1.1 实验材料
实验原材料为莫来石纤维增强SiO2气凝胶复合材料,由国防科学技术大学新型陶瓷纤维及其复合材料国防科技重点实验室制备并提供。它以SiO2气凝胶为基体,莫来石纤维为增强体,采用溶胶-凝胶工艺经超临界干燥技术制备而得,具体制备方法及工艺参数详见文献[28]。
制得的复合材料密度约为0.29 g/cm3。其中,莫来石纤维的主要成分为SiO2和Al2O3,平均直径为4~5 μm,纤维长度为20~40 mm,体积分数约为7%。为了在增强力学性能的同时尽可能降低沿厚度方向隔热性能的损失,大部分增强纤维在气凝胶基体中以铺层形式分布,主要以随机取向分布于面内方向(如图1所示),较少纤维沿厚度方向即面外方向布置。为便于分析受载、受热后显微结构发生的变化,图2给出了高倍率下莫来石纤维增强SiO2气凝胶复合材料原始状态的显微结构,其中SiO2气凝胶基体则由颗粒-团簇结构构成。

图1 增强纤维在气凝胶基体中面内方向上的随机分布特征Fig.1 Random distribution in the in-plane direction of reinforcing fibers in aerogel matrix

图2 莫来石纤维增强SiO2气凝胶复合材料的显微结构(a)面内方向上的莫来石纤维和气凝胶基体;(b)SiO2气凝胶基体中的颗粒-团簇结构Fig.2 Microstructures of mullite fiber reinforced silica aerogel composites(a)mullite fibers and aerogel matrix in the in-plane direction;(b)particles and clusters in silica aerogel matrix
1.2 实验方法
参考室温条件下耐火材料耐压强度实验方法(GB/T 5072—2008)和陶瓷基复合材料压缩强度测试标准(ASTM C 1358-13)开展压缩回弹实验,采用微机控制电子万能试验机(WDW3020)实施。试验机的最大载荷为20 kN,精度等级为0.5。实验中采用上下表面平行的压盘进行加载,加载和卸载速率均为0.01 mm/s。考虑到热防护结构在服役时主要承受的是沿厚度方向的气动压力和舱段内压载荷,因此实验加载方向沿着材料的面外方向。面外压缩试样示意图如图3所示,尺寸为40 mm×40 mm×30 mm。

图3 莫来石纤维增强SiO2气凝胶复合材料面外压缩试样示意图Fig.3 Diagram of out-of-plane compression sample for mullite fiber reinforced silica aerogel composites
面外压缩应力σ为:
(1)
式中:F为实验力;A为标距段原始截面积;L和W分别为标距段长度和宽度。
面外压缩应变ε通过横梁位移的变化进行测量。
(2)
式中:ΔH为试样厚度的变化;H0为试样原始厚度。
为了研究载荷对材料变形恢复能力的影响,开展不同极限应变下的压缩回弹实验,极限应变分别为5%,10%,20%和30%。考虑到热防护材料的高温服役环境,还研究了热暴露温度对变形恢复能力的影响。压缩实验前,将材料预先放入马弗炉(SRJX-5-13A)中进行热暴露,然后在室温条件下开展面外压缩实验,热暴露温度分别为300,600 ℃和900 ℃,保温时间为1 h。使用扫描电子显微镜(JEOL JSM-6010,JEOL JSM-7500)对力学实验前后、热暴露预处理前后试样的组织形貌进行观察分析。
1.3 变形恢复能力评价
为了评估纤维增强气凝胶复合材料在不同实验条件下的变形恢复能力,针对典型的面外压缩加载-卸载应力-应变曲线(图4),定义如下指标:
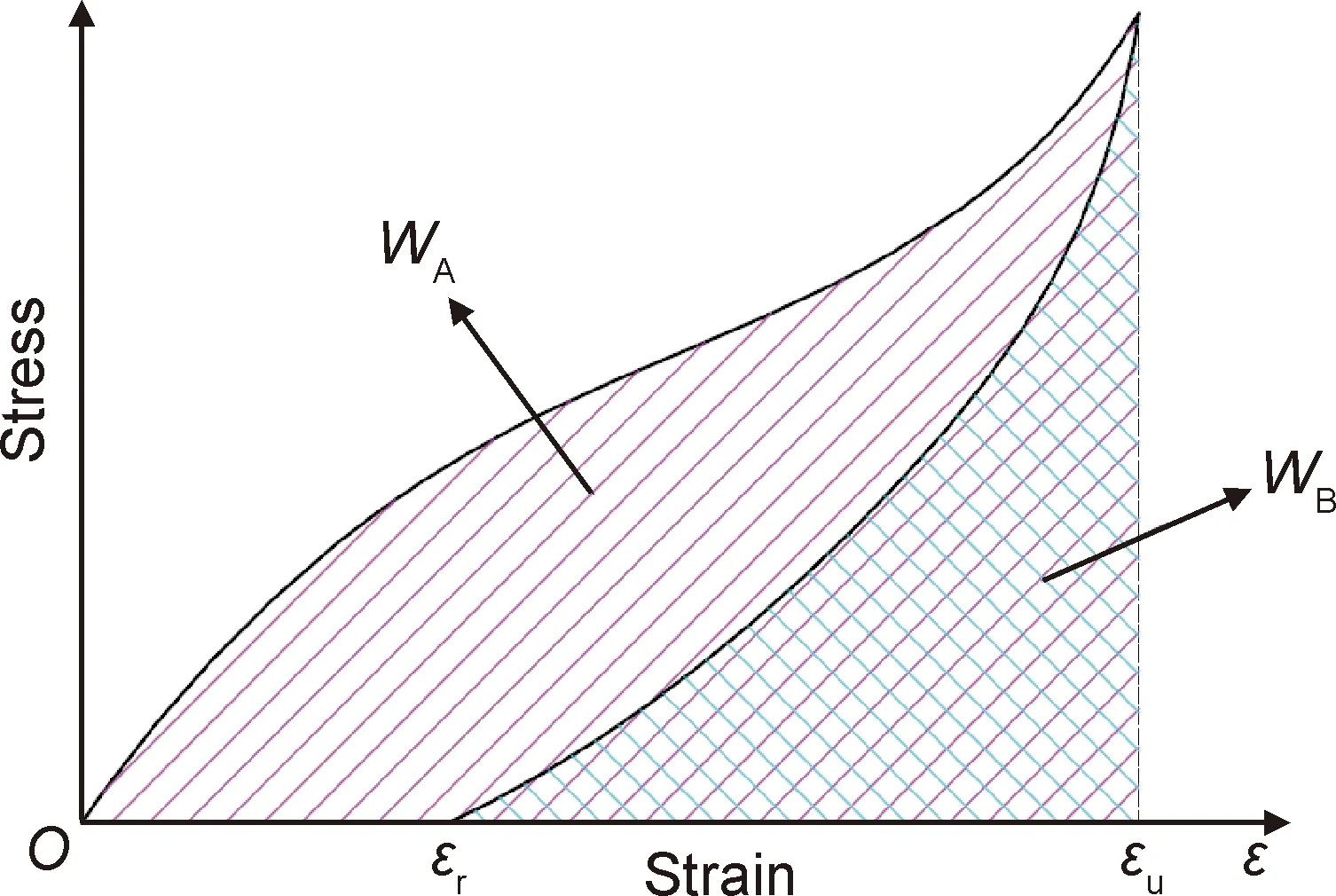
图4 纤维增强气凝胶复合材料典型面外压缩应力-应变曲线Fig.4 Typical out-of-plane compression stress-strain curves of fiber reinforced aerogel composites
(1)不可恢复比例(unrecoverable proportion, UP):
(3)
式中:εr为残余应变(压缩应力下降为0时的应变);εu为极限应变(压缩应力达到峰值时的应变)。
(2)回弹率(resilience ratio, RR):
(4)
式中:WA为压缩加载阶段的压缩功;WB为压缩卸载阶段的压缩功。压缩过程中的压缩功等于应力-应变曲线下的面积,因此WA和WB可以由此获得:
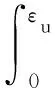
(5)

(6)
式中:σA(ε)是加载阶段的应力;σB(ε)是卸载阶段的应力。
2 变形行为力学建模
通过实验可以获得莫来石纤维增强SiO2气凝胶复合材料在压缩加载-卸载过程中的力学行为表现,其在面外压缩载荷下呈现的特殊非线性特征主要是由于孔洞的塌陷、裂纹的萌生与扩展以及基体组织的密实化,而纤维网络的柔韧性又使其具有一定的弹性和恢复能力。若要建立考虑物理机制的力学模型,十分复杂。考虑到实际工程结构仿真分析的需要,本工作试图建立一种幂函数形式的唯像力学模型,对此类材料的压缩加载-卸载应力-应变曲线加以描述。
加载时,线弹性阶段之后,其切线模量具有先减小后增大的特征,可采用式(7)来描述切线模量随着应力的变化[29]:
(7)
式中:E0为线弹性阶段的模量;σy为压缩屈服应力;σn-1为上一个分析步的压缩应力;α,β,γ,δ均为材料常数。
而卸载时,其应力-应变曲线和极限应力、极限应变相关,可采用式(8)描述切线模量随着应变的变化:
(8)
式中:σu为压缩极限应力;εu为压缩极限应变;εn-1为上一个分析步的压缩应变;k1,k2,m1,m2均为材料常数。
通过对实验获得的应力-应变曲线加载段和卸载段进行微分以获得切线模量,进而利用式(7),(8)进行回归拟合,便可获得相应的材料常数。
3 结果与讨论
3.1 压缩回弹非线性力学行为
图5为莫来石纤维增强SiO2气凝胶复合材料沿面外方向单轴压缩加载-卸载的应力-应变曲线。由于基体中多孔结构的存在,大多数气凝胶复合材料受压时都具有类似的行为特征。根据斜率的变化一般可将曲线划分为3个阶段:第1阶段(应变范围约为0%~5%),曲线斜率相对较高;第2阶段(应变范围约为5%~20%),斜率逐渐降低,并保持较低水平;第3阶段(应变范围大于20%),随着载荷增大斜率增大。

图5 莫来石纤维增强SiO2气凝胶复合材料面外压缩应力-应变曲线Fig.5 Out-of-plane compression stress-strain curves of mullite fiber reinforced silica aerogel composites
在面外压缩加载阶段,材料呈现出典型的非线性特征。上述3个阶段可以分别定义为:线性阶段、屈服阶段和密实化阶段。对应的变形机制为:第1阶段中,气凝胶基体起到主要的承载作用,纳米颗粒骨架结构发生弹性变形,纤维在面外方向上很少排布,起到的承载作用有限;第2阶段中,随着载荷增大,材料开始出现屈服特征,增强纤维组成的网络逐渐起到承载与增韧的作用;第3阶段中,由于基体的密实化和纤维网络的变形,随着应变增加,应力也快速增大。在此阶段中,基体中的颗粒骨架结构已大体被破坏,多孔特征逐渐消失,基体和纤维铺层网络不断被压实。
从图5所示的不同极限应变(5%, 10%, 20%和30%)下面外压缩应力-应变曲线的卸载阶段可以看出,较小极限应变的曲线(5%和10%)与较大极限应变的曲线(20%和30%)之间有明显差异,后者且有更为显著的非线性特征。在卸载阶段,随着应力水平的降低,应变下降的速率逐渐增加。当应力下降为0时,会存在一定程度的不可恢复残余应变,尤其是在较大极限应变(20%和30%)的实验中。
随着极限应变增大,最终产生的不可恢复残余应变也会增加。在加载曲线的屈服阶段和密实化阶段,气凝胶基体中的开孔结构逐渐被破坏,裂纹的不断增加和扩展导致永久变形的产生。而在卸载曲线的初期,由增强纤维所构成的支撑网络的变形逐渐恢复,基本上仍是弹性变形。然而,复合材料产生的塑性变形很难恢复,这主要是由基体孔洞塌陷引起的基体裂纹导致的。所以,卸载曲线后期开始出现显著的非线性特征。
在面外压缩载荷下,基体内开孔结构的破坏以及裂纹的产生与扩展是主要的能量吸收机制,除此之外,界面脱粘与裂纹偏转也起到能量吸收的作用。较大的孔洞易成为裂纹源,引起基体内局部的应力集中,进而导致基体的破坏。图6为莫来石纤维增强SiO2气凝胶复合材料受压后的显微结构(30%极限应变)。可以看出,当受到较大的压缩变形时气凝胶基体产生大量的裂纹。同时,也能观察到裂纹偏转和界面脱粘现象,这些也是主要的增强和增韧机制,许多能量被消耗在纤维和基体之间界面摩擦做功上。

图6 莫来石纤维增强SiO2气凝胶复合材料受压后的显微结构(30%应变)Fig.6 Microstructure of mullite fiber reinforced silica aerogel composites after compression with 30% strain
采用1.3节中定义的评价指标对莫来石纤维增强SiO2气凝胶复合材料的变形恢复能力进行评估,如图7所示。不可恢复比例会随着极限应变增大而增加,回弹率则随着极限应变增大而降低。说明随着极限载荷增加,材料的变形恢复能力下降。这是由于材料在更大的载荷下产生了较多的微观损伤,更多的压缩功被消耗在加载阶段的裂纹萌生和扩展中。气凝胶基体中颗粒团簇之间边界上的连接被破坏,使得骨架网络的连通性下降,这种连接的破坏降低了压力释放后材料发生可逆膨胀的能力。之后,当应力降低到一个较低的水平时,开孔结构便不能再维持原有的弹性[30]。
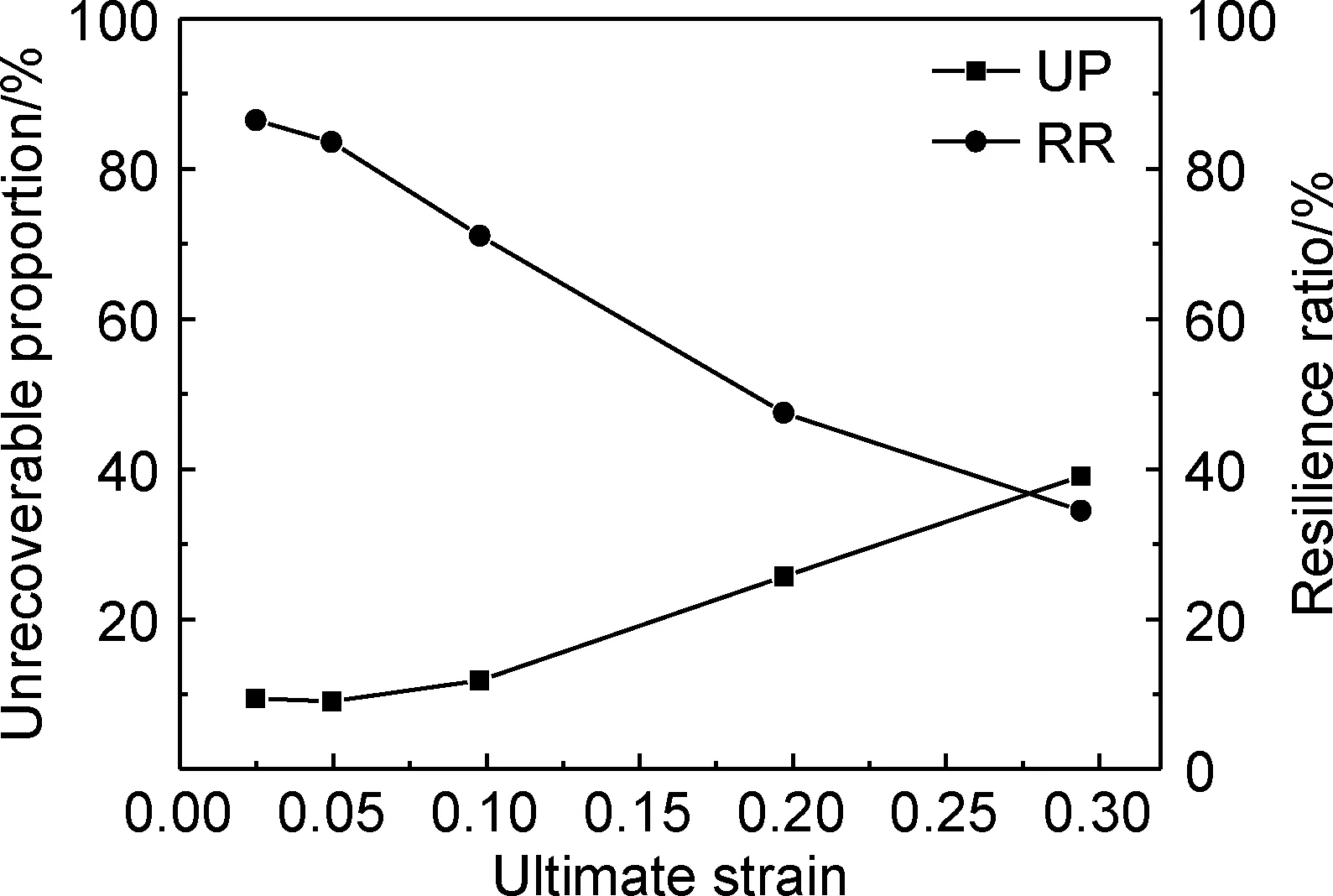
图7 不同极限应变下莫来石纤维增强SiO2气凝胶复合材料的变形恢复能力Fig.7 Deformation recovery ability with different ultimate strains of mullite fiber reinforced silica aerogel composites
3.2 高温热暴露对压缩回弹的影响
图8为经历不同温度热暴露(300, 600 ℃和900 ℃)处理后材料在室温环境中的面外压缩加载-卸载应力-应变曲线,极限应变约为20%。图8中也加入了未经热暴露材料的响应曲线以做比较。从曲线形状可以看出,热暴露处理并未改变材料的基本变形特征,加载曲线中仍包含极限应变以下对应的第1和第2阶段。这说明,经历900 ℃热暴露后莫来石纤维增强SiO2气凝胶复合材料内部仍具有一定的孔结构。但是,高温热暴露使得材料的模量和强度(对应承载能力)显著上升。

图8 不同温度热暴露后莫来石纤维增强SiO2气凝胶复合材料的面外压缩应力-应变曲线Fig.8 Out-of-plane compression stress-strain curves of mullite fiber reinforced silica aerogel composites after different temperature thermal exposure
图9为不同温度热暴露后莫来石纤维增强SiO2气凝胶复合材料的变形恢复能力。可以看出,随着热暴露温度的升高,不可恢复比例增加,回弹率则下降。尤其是经历900 ℃热暴露后,材料受压后的残余应变较高。而从卸载曲线中也看出,应变因应力水平下降而减少的速率明显下降。可以认为,高温环境使得莫来石纤维增强SiO2气凝胶复合材料的变形恢复能力变差。

图9 不同温度热暴露后莫来石纤维增强SiO2气凝胶复合材料的变形恢复能力Fig.9 Deformation recovery ability of mullite fiber reinforced silica aerogel composites after different temperature thermal exposure
上述热暴露对力学特性的影响主要是因为高温使得材料的微观结构发生变化。在较高的温度影响下,气凝胶基体颗粒骨架变得更粗壮,这一影响已在诸多文献中予以阐释[9,31-33]:当暴露在高温中持续受热时,原来较小的气凝胶颗粒-团簇结构(图2(b))会由于物质输运作用互相接近,从而形成较大的颗粒-团簇结构(图10(a)),团簇的聚集使得基体的骨架结构变得粗壮,密实的基体组织具有更好的承载能力。除此之外,纤维和基体之间界面的结合也会变得更加紧密。如图10(b)所示,当复合材料经历高温热暴露后,基体更容易附着在纤维表面,这使得界面解离、裂纹偏转、纤维拔出等增韧机制消耗更多的能量。

图10 高温热暴露对显微结构的影响 (a)颗粒和团簇的聚集;(b)基体和纤维之间的粘连Fig.10 Effect of high temperature exposure on microstructure(a)aggregation of particles and clusters;(b)adhesion between matrix and fiber
当承受面外压缩载荷时,加载阶段中增强纤维网络在压力作用下产生变形,但和压力水平相比,尺寸短且随机分布的纤维网络具有足够的模量和强度来承受载荷作用。当载荷被缓慢撤去时,大多数纤维可以恢复到初始状态。而当受到高温热暴露影响后,虽然基体中原始孔洞的尺寸和数量降低,但是团簇的聚集导致团簇之间较大尺寸孔洞的形成[32]。在压缩应力作用下,这些大孔的坍塌继而引起基体裂纹的形成。大孔的破坏和基体裂纹是不可逆的,这就导致卸载阶段非线性的形成。进一步地,会产生更严重的不可恢复变形。
通过红外光谱检测反映出的化学键状态变化也可以分析高温热暴露带来的影响。残余Si—O—C2H5基团被氧化生成Si—OH基团,而Si—OH基团之间发生缩聚反应形成新的Si—O—Si键,于是气凝胶基体中的颗粒骨架结构得到加强。在形成更强颗粒骨架的同时,Si—O—Si键的产生会导致永久而不可逆的收缩。因此,原有的与氧化而得的Si—OH基团以及由此产生的Si—O—Si键会阻碍回弹行为的发生[32,34]。
3.3 压缩回弹变形行为模拟
基于实验获得的应力-应变曲线数据,采用第2节中的力学模型对莫来石纤维增强SiO2气凝胶复合材料面外压缩的加载和卸载阶段进行应用,以描述其力学行为。针对图5中不同极限应变下的压缩回弹响应数据进行拟合,可以确定式(7)和式(8)中的未知材料常数,如表1所示。图11为不同极限应变下压缩回弹行为模拟与实验数据对比。可以看出,拟合结果与实验数据吻合较好,采用该力学模型可以较好地描述压缩回弹行为。

表1 加载-卸载阶段模型的材料常数值(室温)Table 1 Material constant values of loading-unloading stage models(room temperature)
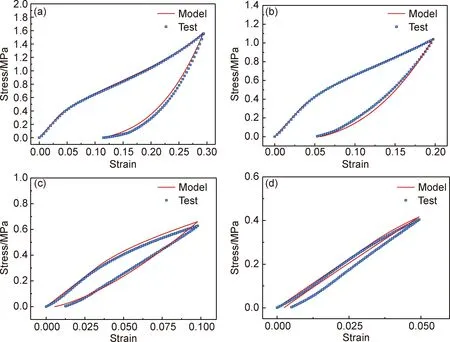
图11 不同极限应变下压缩回弹行为模拟与实验数据对比(a)30%应变;(b)20%应变;(c)10%应变;(d)5%应变Fig.11 Comparison between simulation and experimental data of compression springback behaviors with different ultimate strains(a)30% strain;(b)20% strain;(c)10% strain;(d)5% strain
同样地,不同温度热暴露后材料的压缩回弹行为曲线也可以采用上述力学模型加以建模,获得对应的材料常数,如表2所示。图12为不同温度热暴露后压缩回弹行为模拟与实验数据对比。可以看出,该模型也能够较好地实现模拟不同温度热暴露后材料压缩回弹曲线的目标。由表2可知,对应式(7)等号右端第二项的值很小,这是因为用于拟合的高温热暴露后测得实验数据对应的极限应变在20%左右,包含加载过程的第1阶段和第2阶段,第3阶段切线模量快速上升的部分很少。

图12 不同温度热暴露后压缩回弹行为模拟与实验数据对比(a)300 ℃;(b)600 ℃;(c)900 ℃Fig.12 Comparison between simulation and experimental data of compression springback behaviors after different temperature thermal exposure (a)300 ℃;(b)600 ℃;(c)900 ℃

表2 加载-卸载阶段模型的材料常数值(高温)Table 2 Material constant values of loading-unloading stage models(high temperature)
值得注意的是,由于以上获得的是不同温度热暴露后在室温环境中的实验数据,而非不同测试温度下的实验数据,因此本工作中的结果表示的并不是材料特性随着温度发生的变化,但可以在设计中近似使用。进一步地,后续工作中针对不同测试温度下获得的材料响应曲线,可以在模型中加入温度相关项以描述温度的影响。
4 结论
(1)在面外单轴压缩载荷作用下,莫来石纤维增强SiO2气凝胶复合材料在加载和卸载阶段的力学行为呈现出显著的非线性特征,这主要是由气凝胶基体内孔洞塌陷和裂纹形成导致的。此外,压缩回弹行为及变形恢复能力则与材料承受的载荷水平相关。
(2)高温热暴露预处理会对莫来石纤维增强SiO2气凝胶复合材料的压缩回弹行为产生影响,热暴露温度越高,变形恢复能力越差。基体颗粒-团簇结构受高温影响发生的聚集现象、大尺寸孔洞的形成和塌陷是导致上述情况的主要原因。
(3)本工作建立的唯像力学模型可以用来描述莫来石纤维增强SiO2气凝胶复合材料在压缩加载-卸载时的应力-应变曲线,拟合结果与实验数据吻合较好,可用于实际工程中热防护结构的仿真分析。

