未满载压载水的单点系泊软刚臂纵向静刚度
刘勖恒
(清华大学 土木水利学院, 北京 100084)
0 引 言
海洋平台是开发海洋资源的关键装备,塔架软刚臂单点系泊装置通过软刚臂将漂浮的海洋平台系泊在固定单点塔架上,这是目前固定海洋平台的一种普遍方式,在国内外得到广泛应用。软刚臂单点系泊装置的设计、制造、维护长期被国外少数公司所垄断[1],我国已开始自主研发软刚臂单点系泊系统。软刚臂系泊与缆链系泊的主要区别如下:软刚臂在自重和压载水重力作用下具有水平刚度,能为海洋平台提供水平回复力,当海洋平台靠近单点塔架时对其产生推力,当海洋平台远离单点塔架时对其产生拉力,限制浮动的海洋平台在风、浪、流等环境载荷作用下的运动,系泊海洋平台并防止海洋平台与单点塔架发生碰撞。
目前人们对软刚臂进行大量的理论建模、数值计算和缩比试验,涉及软刚臂的刚度特性、结构强度、疲劳,以及软刚臂系泊系统与海洋浮动平台在复杂海洋环境载荷作用下的耦合动力学等。例如:FAN等[2]分析软刚臂单点系泊系统原型试验测量方法及其精度;田冠楠等[3]对指定环境工况下的软刚臂单点系泊系统载荷进行数值分析,将其与模型试验结果进行对比,验证数值模型的有效性;吕柏呈等[4-5]建立软刚臂多体动力学方程,分析软刚臂系泊系统的动力学特性;张凤伟等[6]采用模型试验和数值计算方法研究软刚臂系泊下浮式液化天然气存储及再气化装置的动力学特性;袁威等[7]建立系泊力、平台水平位移与软刚臂结构形式之间的关系,以确定不同吨位的浮式生产储卸油装置(Floating Production Storage and Offloading,FPSO)适用的最佳软刚臂结构形式;金锋等[8]建立软刚臂单点系泊系统的多体动力学模型,构建保辛数值积分方法,计算系统动力学响应和系泊力;胡勇等[9]用ADAMS软件分析软刚臂系泊系统与平台的多自由度耦合运动;尧白莲等[10]分析软刚臂单点系泊的横向刚度特性。
现有的研究都针对水舱满载压载水的软刚臂,此时软刚臂的重心在其结构上的相对位置保持不变,其静力学平衡方程和动力学方程相对容易建立。但是,由于软刚臂系泊系统实际运行的长期性以及运行环境的复杂性和不确定性,在非正常情况下,一旦软刚臂压载水舱未满载压载水,压载水会随着软刚臂的运动在水舱内流动,软刚臂的重心随之在其结构上发生移动,导致软刚臂的刚度特性不同于水舱满载压载水的正常工况。
本文针对水舱未满载压载水的软刚臂纵向静刚度问题,建立软刚臂纵向静回复力矩随转角变化的理论模型和计算方法,描述单点系泊软刚臂系统在未满载压载水的静态刚度特性,为软刚臂和海洋平台系统在非正常情况下的力学分析提供基础。
1 水舱轴线与压载水水面夹角
软刚臂由2个盛水的圆柱形密封压载水舱和2个连杆呈A字形组成,如图1所示。连杆与水舱的1个端面固定连接,2个连杆分别与对应水舱的轴线共线并汇聚于点O,在O点与固定单点塔架铰接连接。圆柱形水舱的半径为r,长度为Lc,忽略水舱壁厚;连杆长度为Lb;软刚臂的2个水舱轴线之间的夹角为2γ。2个长度均为La的系泊腿一端分别与2个水舱外壁铰接连接,连接点至原点O的连线在水舱轴线方向的投影距离为Ld,系泊腿另一端与海洋平台上的系泊支架铰接连接。水舱、连杆和系泊腿均视为刚体,设单个水舱满载时压载水量为W0,单个水舱未满载时压载水量为kW0(0≤k<1),k为压载舱的装载率。

图1 软刚臂几何尺寸及整体和局部坐标系
如图1所示:建立整体坐标系O-XYZ,其中X轴沿2个水舱轴线的角平分线方向(EX=(1,0,0)),Y轴竖直向上(EY=(0,1,0)),Z轴沿软刚臂的转动轴方向(EZ=(0,0,1));以整体坐标系的原点O为原点建立局部坐标系O-xyz,x轴沿水舱轴线方向,z轴为该竖直面的法线方向,y轴位于水舱的垂直横截面内。忽略海洋平台绕单点塔架的旋转运动及平台艏摇,仅考虑软刚臂绕Z轴的旋转运动,旋转角度φ定义为软刚臂的2个水舱轴线形成的平面与水平面之间的夹角。
由于对称性,取软刚臂的一半结构进行研究。如图2所示,P为初始水舱自由端面(左端面)的中心点,该点在软刚臂绕Z轴旋转φ后运动至Q点,R点为P点和Q点在Z轴上的投影点,LOP=LOQ=L=Lb+Lc,LPR=lQR=a=Lcosγ,PR与QR之间的夹角为φ。在三角形PQR中,求得PQ长度为
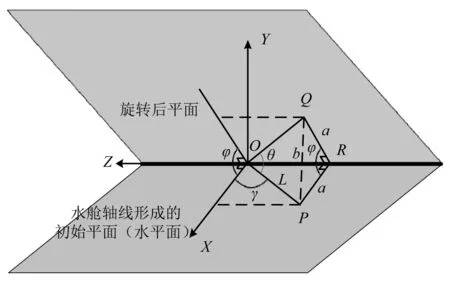
图2 水舱轴线与压载水水面之间夹角示例
(1)
在三角形PQO中,求得PO与QO的夹角θ为
(2)
θ即为软刚臂旋转后水舱中的水面与水舱轴线之间的夹角。
2 压载水舱中的水面位置
在整体坐标系下,X轴的方向向量EX绕Y轴旋转γ角度,然后再绕Z轴旋转φ角度,即得到局部坐标系的x轴在整体坐标系中的方向向量nx。利用罗德里格旋转公式,空间向量B绕单位向量A旋转角度α后得到向量的表达式为
B′=Bcosα+(A×B)sinα+A(A·B)(1-cosα)
(3)
得到nx为
nx=n′xcosφ+(EZ×n′x)sinφ+EZ(EZ·n′x)(1-cosφ)
(4)
式中:
n′x=EXcosγ+(EY×EX)sinγ+EY(EX·EY)(1-cosγ)=(cosγ,0,-sinγ)
(5)
同理,旋转EY和EZ可以得到局部坐标系y和z轴在整体坐标系下的方向向量ny和nz。
若任意一个空间向量在整体坐标系下的分量为[T1,T2,T3]T,在局部坐标系下的分量为[t1,t2,t3]T,则两者之间的转换关系为
(6)
式中:Λ为坐标转换阵
Λ=[nxnynz]
(7)
于是,整体坐标系X轴在局部坐标系下的方向向量为
eX=ΛTEX=[nx[1]ny[1]nz[1]]T
(8)
用过压载水舱轴线的竖直平面(垂直于水舱内水面)将水舱切开,则水舱在局部坐标系xy平面的图形如图3所示,水面以下为压载水,水面以上为空,水面与水舱轴线之间的夹角为θ,由式(2)给出。水面在xy平面内与水舱左端面、右端面、轴线、上表面、下表面交点的x轴坐标分别为xa、xb、xc、xu、xd,其中:xa=Lb+Lc,xb=Lb,xc∈[xb-r/tanθ,xa+r/tanθ],xu=xc+r/tanθ,xd=xc-r/tanθ。

图3 局部坐标系xy平面中的水舱截面
根据xu、xc、xd与xa、xb之间的关系,水舱内水面位置分为8种情况,分别如图4所示。

图4 水舱水面的8种情况
在局部坐标x轴横截面(yz平面)内,根据水舱的水面位置,分为水面在z轴之上和在z轴之下两种情况(见图5),其中,水面距z轴的距离为h(x)。
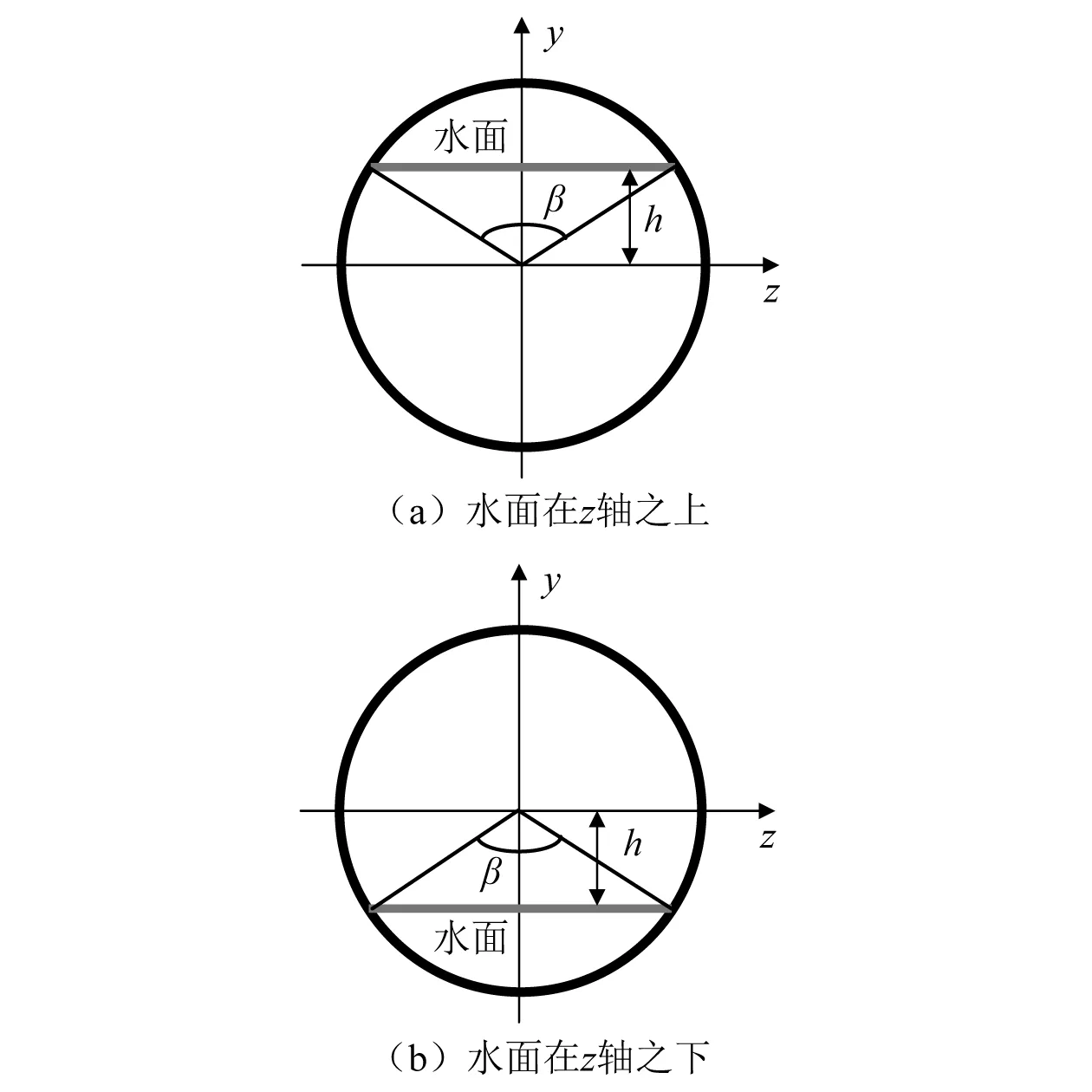
图5 水舱横截面上水面与z轴的关系
容易计算水舱横截面上的水面积为
(9)

根据图4中水面的8种情形,水舱中水的重量W为

(10)
对于2个水舱的压载水装载率都为k的软刚臂,当其绕整体坐标系Z轴的转角为φ时,可根据载水量kW0确定xc,并判断水舱中当前水面属于上述8种情形中的哪一种。由于水舱载水量函数的分段特性,难以直接根据kW0解方程计算xc,采用简单的数值方法确定xc:(1) 当0≤k≤0.5时先设定xc等于其最大取值xc=xa+r/tanθ,然后逐渐减小xc,每次均匀减小Δxc=(xa-xb+2r/tanθ)/n,n为给定的整数;当0.5 考虑软刚臂水舱横截面上水的微元dxdy,其在局部坐标系下的位置向量为s,所受的重力竖直向下,该微元重力对软刚臂转轴(整体坐标系Z轴)的力矩为dM=ρdydze,其中:ρ为水密度;e为该微元至整体坐标系YZ平面的距离,e=eX·s。则水舱中的压载水对软刚臂转轴的重力矩M为 (11) 设水舱为均匀圆柱壳体结构,重量为Ws,结构质心位于水舱几何中心,在局部坐标系下位置为(Lb+Lc/2,0,0),则水舱结构自重对软刚臂转轴的力矩为 Ms=Ws(Lb+Lc/2)cosγcosφ (12) 软刚臂的总回复力矩为2(M+Ms),于是建立软刚臂纵向静回复力矩与转角之间的关系。 计算流程如图6所示。 图6 软刚臂纵向静回复力矩计算流程 利用所建立的软刚臂纵向静回复力矩模型,取r=2 m,La=40 m,Lb=12 m,Lc=12 m,Ld=23 m,γ=20°,W0=27.64 t,n=10 000, Δφ=0.09°,计算得到不同压载水装载率下的软刚臂压载水的纵向静回复力矩随旋转角度的变化曲线(见图7),软刚臂纵向总静回复力矩随旋转角度的变化曲线(见图8)。图7中:曲线M_Full为用固定质心方法计算得到的满载时的曲线,曲线M_Full_k(k=0.10,0.30,0.50,0.70,0.90,0.99)为满载压载水时的压载水回复力矩乘以装载率k(k=0.10,0.30,0.50,0.70,0.90,0.99)得到的曲线,其中曲线M_Full_0.99与M_Full 基本一致,不再画出;曲线M_k(k=0.10,0.30,0.50,0.70,0.90,0.99)为用本模型计算得到的装载率k(k=0.10,0.30,0.50,0.70,0.90,0.99)下的压载水回复力矩曲线。图8中M_k+Ms、M_Full_k+Ms为相应的压载水回复力矩与软刚臂结构重力矩之和。由图7和图8可知,不同压载水装载率下的回复力矩曲线之间不存在线性比例规律。 图7 软刚臂压载水纵向静回复力矩随旋转角度的变化 图8 软刚臂纵向总回复力矩随旋转角度的变化 图9为考虑水流动和不考虑水流动两种方法计算的压载水纵向静回复力矩之间的相对误差,相对误差定义为(M_Full_k-M_k)/M_k。由图9可知:当压载水装载率较小时,相对误差较大,随着压载水装载率的逐渐增大,二者的差异越来越小;当压载水装载率为0.99时,软刚臂回复力矩曲线与满载压载水的曲线很接近;当旋转角度接近0°,即软刚臂基本水平时,2种情况下的压载水质心一致,因此回复力矩相同;随着角度从0°开始增大,相对误差迅速增大,然后保持缓慢增大;当角度接近90°时,相对误差迅速增大,但此时的绝对误差非常小。 图9 不同压载舱装载率下压载水纵向静回复力矩与固定质心静回复力矩之间的相对误差 推导单点系泊软刚臂未满载压载水时的静回复力矩模型和计算方法,算例计算结果表明,在水舱未满载时,水的流动会导致软刚臂质心发生变化,软刚臂回复力矩与相同重量下固定质心的软刚臂回复力矩曲线有较大差异,并且压载水装载率越小二者差异越大。需要指出的是,模型假定软刚臂结构对称,当2个水舱中的载水量不相等时,重力会产生扭矩,使软刚臂产生绕X轴的附加转动,对于这种情况,可以在本建模方法的基础上建立其静力学模型。此外,本模型忽略了动态效应,没有考虑未满载时压载水在软刚臂旋转过程中复杂的液面晃动问题。3 纵向静回复力矩

4 算 例



5 结 论

