基于Abaqus的合成纤维缆动刚度特性
张若瑜, 范子逸, 陈六合, 赵同岩
(天津大学 a. 建筑工程学院; b. 港口与海洋工程教育部、天津市重点实验室, 天津 300072)
0 引 言
随着全球经济社会的进步与发展,世界各国对海洋油气资源的需求愈发迫切,人类对海洋的开发也逐渐向深水和超深水海域迈进。为满足深水环境的工作需要,更适用于深水的绷紧式系泊系统得到广泛的应用和发展。合成纤维缆作为绷紧式系泊系统的主要用缆,与传统钢缆相比,具有更复杂的力学特性[1-2]。
目前学术界认为动刚度是合成纤维缆材料非线性的主要表现形式。动刚度是缆索在循环载荷作用下张力幅值与应变幅值的比值。DEL VACCHIO[3]针对聚酯缆设计模型试验,发现缆索的动刚度大小主要受缆索平均张力、张力幅值和载荷周期的影响。BOSMAN等[4]基于DEL VACCHIO提出的经验公式,设计相关的敏感性试验,发现缆索平均张力对动刚度的影响最大。刘海笑等[5]、陈映宇等[6]、黄泽伟[7]在前人的基础上优化针对绷紧式系泊系统合成纤维缆的动刚度计算方法,并提供计算算例和参数,使用有限元方法求解合成纤维缆的运动响应。
在合成纤维缆动力响应模型计算方面,目前有集中质量法、有限差分法和有限元法等3种方法。在缆索动力响应计算的具体研究中:TJAVARAS等[8]在考虑拉伸弯曲扭转耦合作用的基础上,将系泊缆离散为多个单元,并基于欧拉-伯努利梁理论,建立各单元的运动方程;唐友刚等[9]在考虑系泊缆拉伸弯曲扭转变形的基础上,基于细长杆理论,分析深水Spar平台系泊缆的固有模态;王飞[10]基于集中质量法建立考虑扭转和弯矩作用的水下拖缆动力学模型,给出完整的三维曲率、弯矩、扭矩和剪力的确定方法。
为研究合成纤维缆的动力特性,本文采用有限元软件Abaqus求解合成纤维缆的运动响应,并采用UMAT子程序模拟缆索的动刚度特性,分析缆索动刚度对缆索动力特性的影响,此外还考虑缆索自重、外激励作用和海流作用对动刚度的影响。
1 Abaqus的AQUA模块和UMAT子程序
1.1 AQUA模块
Abaqus的AQUA模块拓展了Abaqus/Standard在海洋中的应用[11]。AQUA模块主要用于海洋管道装置的建模分析或海洋立管问题的分析等。此外,Abaqus/AQUA还可对水下或部分处于水下的结构物施加稳定的海流、波浪和风载荷。
AQUA模块适用于Abaqus中梁单元、管单元、桁架单元、弯头单元和特定刚体单元的流体阻力、浮力和惯性力计算。在计算时可选择线性分析或非线性分析。
AQUA模块可应用于Abaqus主程序[12]的静态分析、动态显式分析、特征频率提取分析、使用直接积分的隐式动态分析。
1.2 UMAT子程序
1.2.1 概述
除了自带的众多模块外,Abaqus还提供功能强大的用户定义子程序接口。基于这些子程序,用户可基于Abaqus内部的计算逻辑开发适用于自身分析需求的程序。常用的用户定义子程序有UMAT用户材料子程序和UEL用户单元子程序。
UMAT子程序采用Fortran语言编辑,将Abaqus与Fortran程序进行关联,可在计算时调用编写的Fortran子程序[13]。
1.2.2 UMAT调用原理及流程
UMAT的关键问题在于给出准确的雅各比矩阵(应力-应变关系矩阵)。在第n个UMAT调用增量步开始前,子程序从主程序调用当前的应力σn和应变εn,并设定一个应变增量dεn+1,根据子程序中给出的雅各比矩阵DDSDDE,得到第n+1增量步的应力σn+1。在增量计算完成后,子程序会更新雅各比矩阵、应力-应变矩阵和相关的状态变量矩阵,并将其返回至主程序中,以备下一个增量步的调用。
1.3 缆索动刚度的UMAT子程序开发
1.3.1 合成纤维缆动刚度特性
合成纤维缆的运动特性主要取决于缆索的轴向刚度特性,合成纤维缆的动刚度特性主要体现在轴向刚度的变化上。目前在进行相关分析计算时,对合成纤维缆轴向动刚度k的计算方法主要为动刚度经验公式[14]:
(1)
式中:E为单元刚度;A为系泊缆截面积;MBL为缆索的最小断裂强度;Lm为平均张力占MBL的百分比;La为动态张力幅值占MBL的百分比;α、β、γ均为与缆索结构及材料有关的参数,具体如表1所示。

表1 动刚度经验公式参数
1.3.2 计算流程
依据UMAT调用流程及合成纤维缆动刚度经验公式,得出动刚度的计算流程[15]如图1所示。
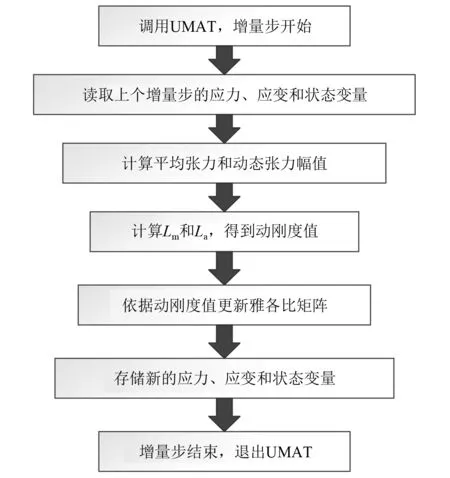
图1 动刚度经验公式在UMAT中的实现流程
在本算例中,考虑到外激励为简谐位移,参考其他计算动刚度的文献,认为缆索的平均张力始终为预张力,即Lm为固定值。
1.3.3 雅各比矩阵推导
雅各比矩阵即单元的应力-应变关系矩阵,建模使用的单元为杆单元。由于杆单元在设定上只有轴向应力和应变,因此杆单元为一维单元,相应的,杆单元的雅各比矩阵也为一维矩阵,杆单元的应力-应变关系可用其轴向刚度直接表示,因此在考虑动刚度的经验公式之后,杆单元的雅各比矩阵为
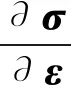
(2)
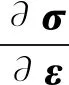
2 算例及分析思路
2.1 系泊参数
选取工作水深为1 500 m的Spar平台绷紧式系泊系统作为研究对象,其系泊布置[16-17]如图2所示。
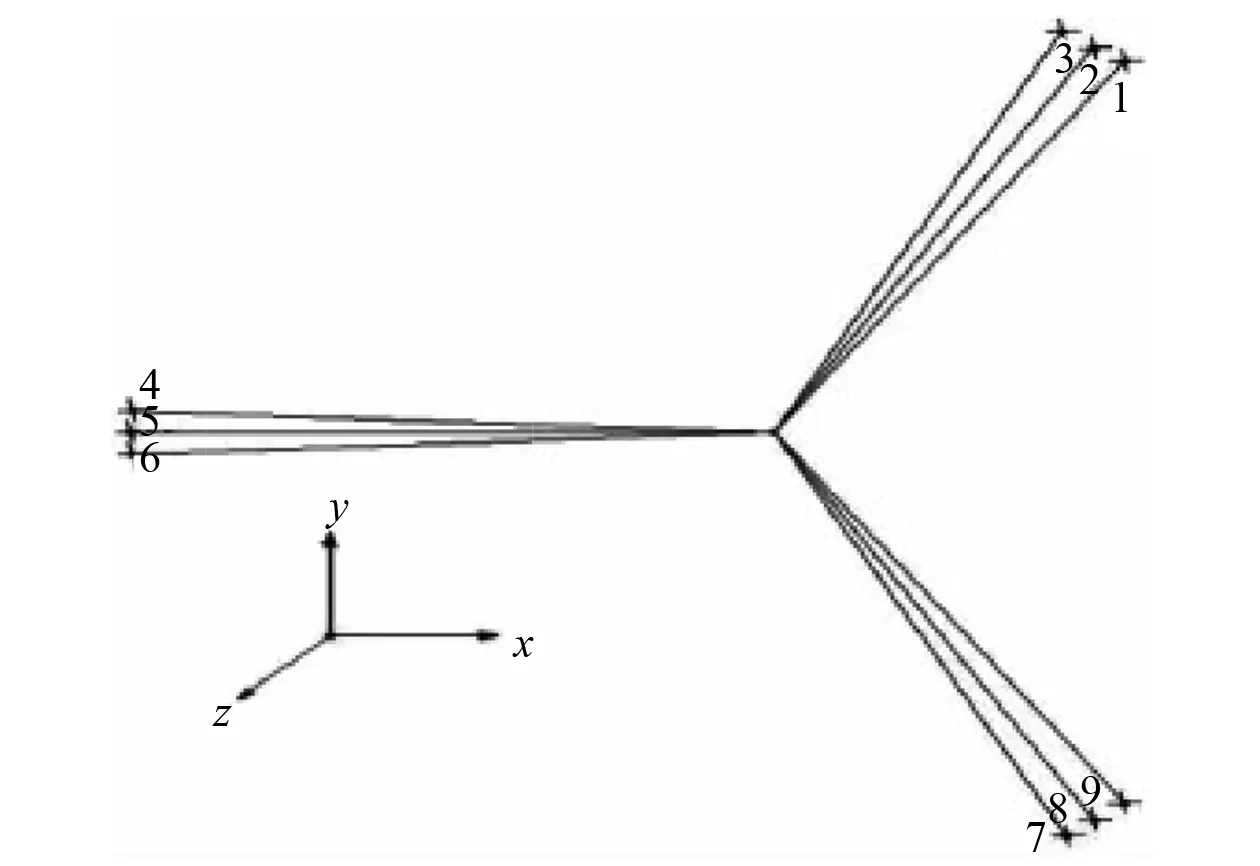
图2 系泊系统平面布置
将Spar平台简化为一个点,系泊系统分为3组缆,每组3根,每组间隔120°,组内每根缆索间隔为5°。为方便计算,选择与x轴平行的5号缆为研究对象。在缆索的上端点施加一个x方向的简谐位移,位移函数为x(t)=x0sin(2πt/T),其中:t为时间;位移幅值x0=5 m;位移周期T=10 s。单缆运动的具体示例如图3所示。图3中:H为导缆孔与水下系泊点的垂直距离;S为系泊缆的水平跨距;O点为简化的Spar平台位置。
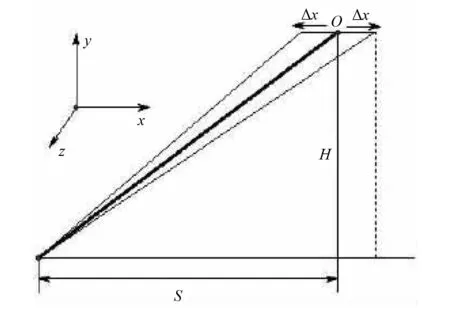
图3 单缆运动示例
系泊系统具体参数如表2所示。

表2 系泊系统参数
2.2 分析思路
对于系泊缆索这样的细长体结构,Abaqus中比较适合的单元是梁单元(beam)和杆单元(truss)。考虑到杆单元中只存在轴向应力和应变,这与只考虑拉伸情况下的系泊缆索较为符合,因此选用杆单元模拟海洋系泊缆索。
在缆的初始位形方面,与悬链线式系泊不同,合成纤维缆适用的绷紧式系泊无须进行初始位形计算,在初始时刻可看作一条直线段,线段下端固定在海床上,上端与导缆孔相连。
在载荷作用方面,系泊缆浸没在水中,主要受到的静力有重力、浮力和上部浮体给予的预张力,受到的动力包括波浪及海流引起的拖曳力和惯性力,以及为分析动力特性人为添加的简谐外激励力。
依据上述载荷情况,可将分析过程分为静力分析步和动力分析步,在静力分析步中添加重力、浮力和预张力,在动力分析步中添加位移外激励、拖曳力和惯性力,随后调用Abaqus计算模块计算缆索的动力响应。
3 计算结果分析
3.1 静刚度和动刚度张力
以缆索首端为研究对象,分析缆索在静刚度情况下的张力情况,在Abaqus/CAE中直接定义材料的刚度,不引入UMAT用户自定义材料,并与文献[17]的张力计算结果进行比较,如图4所示。
由图4可知,Abaqus算法作为只考虑缆索拉伸的方法,所获得的计算结果与同样只考虑缆索拉伸的文献[17]计算结果基本吻合,这说明用Abaqus模拟缆索张力是可行的。且由于所施加的外激励为简谐外激励,因此缆索张力变化也呈简谐趋势,且变化周期与外激励周期相近。

图4 静刚度张力结果对比
随后,在Abaqus中加入UMAT调用,考虑缆索的动刚度。计算所得的缆索首端动张力和动刚度结果如图5和图6所示。
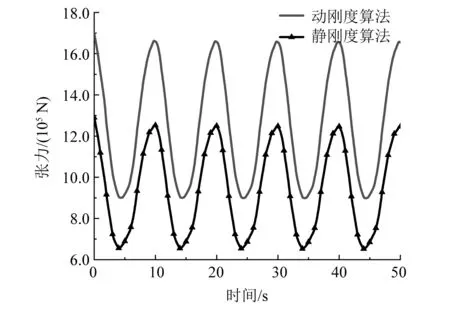
图5 张力计算结果对比
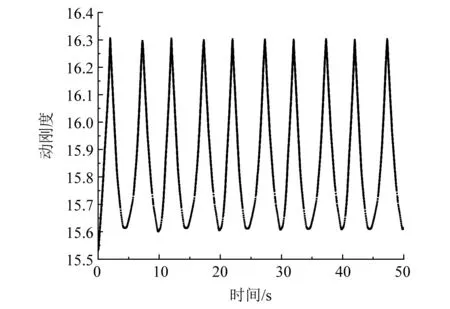
图6 动刚度计算结果
在缆索的动张力方面:从张力数值上看,由于缆索的刚度大幅增加,考虑动刚度后,缆索的动张力在数值上明显大于静刚度下的张力,其中张力峰值增加约450 kN,增幅约36%;从张力的变化趋势来看,考虑动刚度后,动张力仍呈简谐变化,且周期与外激励周期相近,但由于考虑动刚度后轴向刚度增大,张力的变化幅值随之增大,与静刚度相比,幅值增加约200 kN,增幅约33%。
在缆索的刚度方面:从刚度数值上看,考虑动刚度后,缆索的刚度明显增大,缆索的动刚度在15.6~16.3这一范围内波动,与初始值12.2相比,增大27.9% ~33.6%;从动刚度的变化趋势来看,由于动张力呈简谐变化,而动刚度与张力线性相关,因此缆索动刚度的变化呈现出一定的周期性。
3.2 首尾端缆张力对比
在传统的缆索张力算法中,通常认为整根缆的张力保持一致。事实上,由于合成纤维缆本身长度较长,因此张力分布在长度方向上必然存在变化。此外还考虑缆索浮力和重力的作用,这2种载荷对不同位置处的缆索微段的影响也不同。
图7和图8分别为静刚度和动刚度情况下缆索首端和尾端张力时程图。
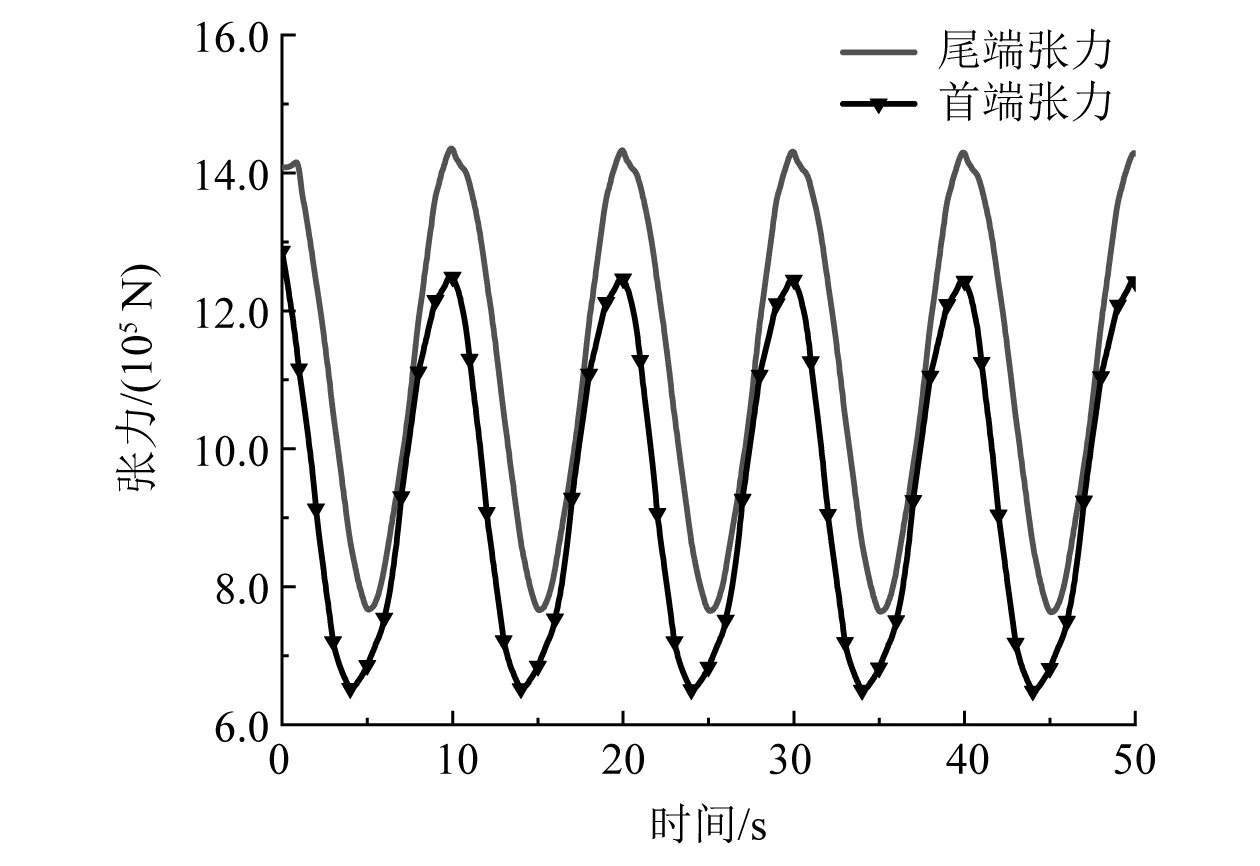
图7 静刚度情况下首尾端张力对比
由图7和图8可知,无论在静刚度还是动刚度情况下,缆索首尾端的张力时程都存在较大差异,且考虑动刚度对这种差异没有明显影响。

图8 动刚度情况下首尾端张力对比
从张力数值上看,由于重力和浮力的影响,缆索尾端的张力始终大于首端的张力。考虑静刚度时,张力峰值增大约12%;考虑动刚度时,张力峰值增大约8.3%。
从缆索张力的变化趋势来看,无论是静刚度情况还是动刚度情况,缆索首尾端张力的变化趋势基本保持简谐变化,且变化周期与外激励周期相近。缆索尾端与首端张力变化的区别主要在于尾端张力的变化稍微滞后于首端张力的变化。上述现象源于缆索长度对张力变化产生的影响。在有限元计算中:缆索首端直接受到外激励作用,缆索发生位移后,张力会直接产生变化;缆索尾端距离运动点较远(本算例为2 058 m),缆索上端位移需要经过一段时间的传导后才能影响尾端,进而改变缆索张力。在缆索长度较短时,张力变化滞后的现象并不明显,而缆索长度越长,位移传导的时间就越长,张力变化滞后的现象就越显著。
合成纤维缆适用的绷紧式系泊系统适用于深水和超深水,系泊缆长度较长,因此这种滞后现象在张力计算中不能忽略。
经分析,缆索首尾端缆段张力变化存在明显差异,可证明传统缆索张力算法中认为整根缆的张力变化始终保持一致的做法不准确。
3.3 自重对缆索张力和动刚度的影响
海洋工程中常用的合成纤维缆重量普遍较轻,以本算例为例,缆索干重为338.1 N/m,考虑浮力作用后湿重仅为-87.2 N/m,与系泊钢缆相比,重量非常小。因此,在之前的一些涉及绷紧式系泊合成纤维缆张力计算的研究中,为简化计算,往往会直接忽略缆索自重,认为自重对缆索张力几乎没有影响。
为分析自重是否会对缆索张力产生影响,分别计算动刚度下考虑缆索自重和忽略缆索自重两种情况,2种情况下缆索的首尾端张力如图9~图12所示。
由图9可知,缆索自重对缆索首端张力的影响较小,考虑自重后,张力峰值几乎不变,张力谷值下降约5.3%。由图10可知,缆索自重对首端动刚度影响也不大,考虑自重后,动刚度峰值几乎不变,部分动刚度谷值下降约0.6%。
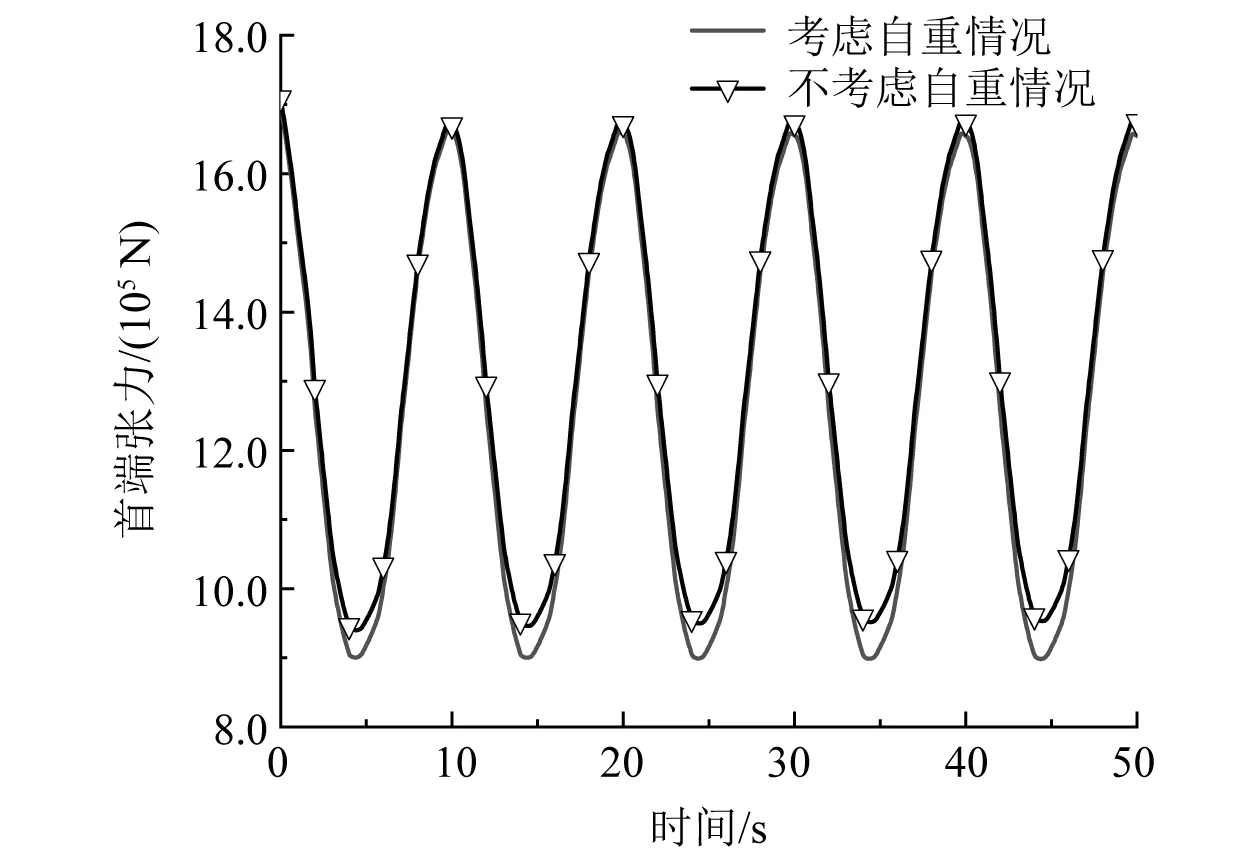
图9 缆索自重对首端张力的影响
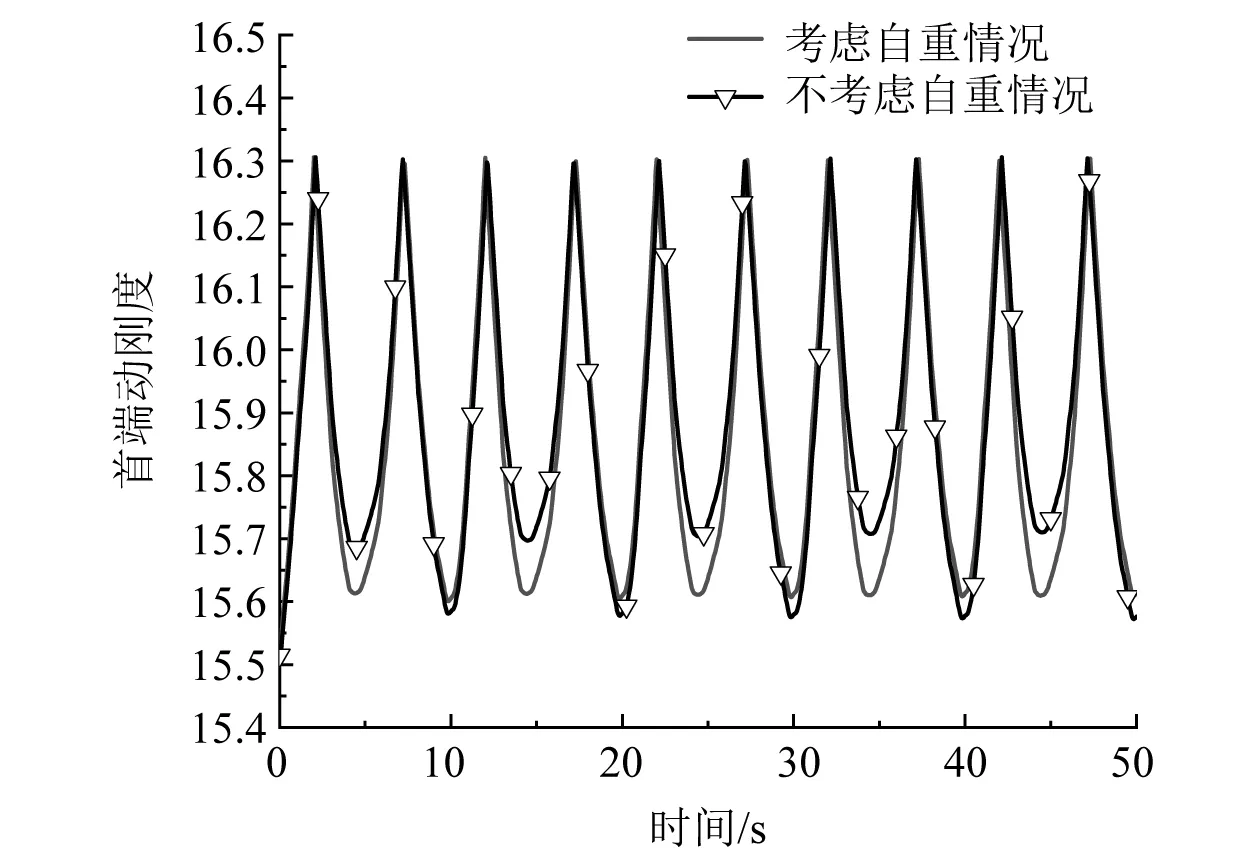
图10 缆索自重对首端动刚度的影响
由图11和图12可知,缆索自重对缆索尾端的张力影响较为明显。从张力时程上来看,考虑缆索自重后:缆索尾端的张力峰值增加约130 kN,增加约7.6%;张力谷值增加约80 kN,增加约8.7%。从动刚度时程来看,缆索尾端动刚度峰值几乎不变,动刚度谷值的改变约1.3%。

图11 缆索自重对尾端张力的影响

图12 缆索自重对尾端动刚度的影响
综上所述,自重对缆索张力特性有较大影响,在张力计算中不能忽略,且对尾端的影响明显大于首端。此外,由于缆索干重较轻,在考虑浮力之后,湿重为负值,因此缆索的尾端张力大于首端张力。
3.4 海流力对缆索张力和动刚度的影响
分析海流力的变化对缆索张力和动刚度的影响。分别取海平面处海流流速为2 m/s、1 m/s(流速方向为全局坐标系的x轴正向)和无流情况,分析不同流速下缆索首端的张力和动刚度。具体情况如图13和图14所示。

图13 海流力对缆索张力的影响
由图13可知,海流力的变化会引起缆索张力的变化。与无流情况相比:当流速为1 m/s时,缆索张力峰值降低约2.9%,谷值降低约5.3%;当流速为2 m/s时,缆索张力峰值降低约5.8%,谷值降低约10.5%。
由图14可知,与无流情况相比,有流速情况下的动刚度峰值无明显变化:当流速为1 m/s时,动刚度谷值改变约0.6%;当流速为2 m/s时,动刚度谷值改变约1.3%。
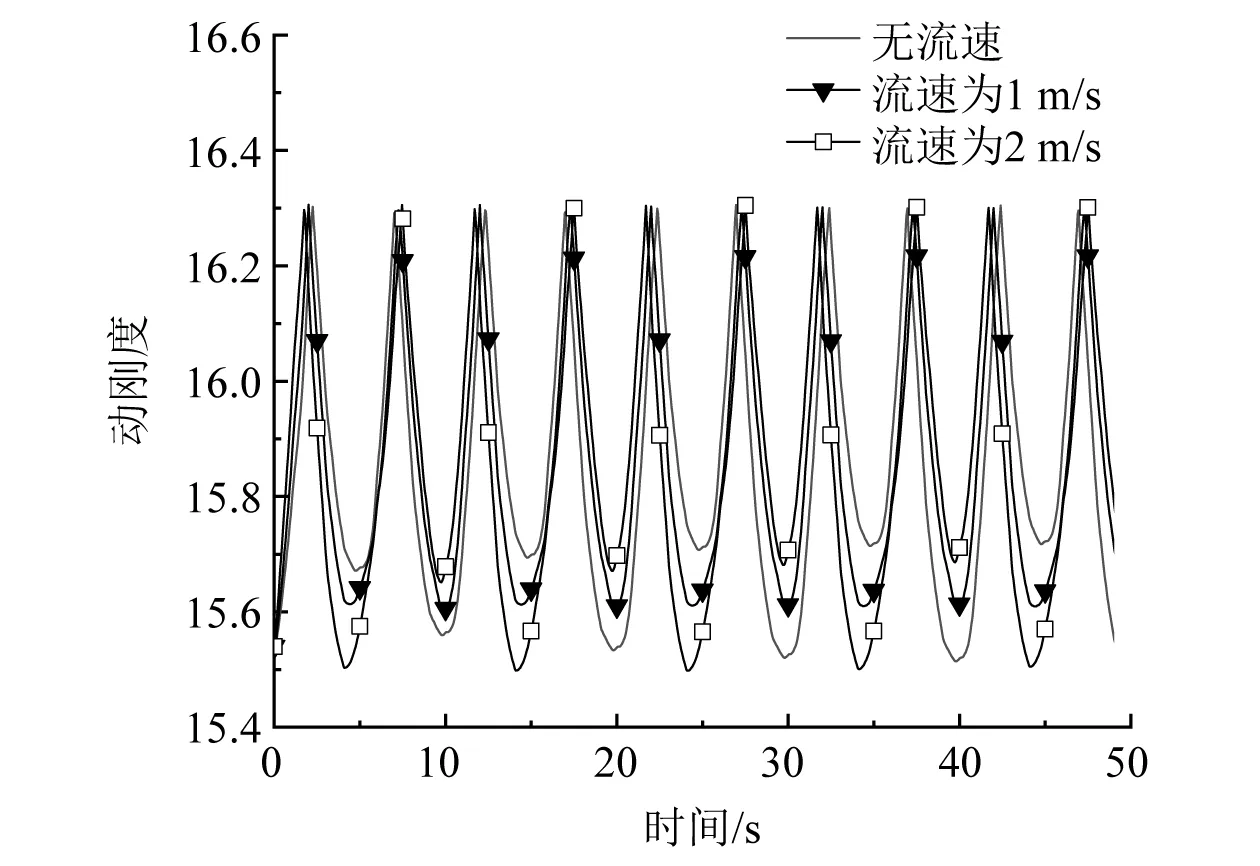
图14 海流力对缆索动刚度的影响
综上所述,海流力对缆索的张力和动刚度有一定的影响,且流速的影响基本呈线性特征,虽然在数值上的影响不大,但不可忽略。
3.5 外激励幅值及周期变化对缆索张力和动刚度的影响
改变缆索顶部运动的幅值和频率,分析运动幅值和频率的变化对缆索张力和动刚度的影响。
3.5.1 外激励幅值的影响
保持位移周期T=10 s不变,分别取位移幅值x0为5 m、10 m、15 m。计算结果如图15和图16所示。
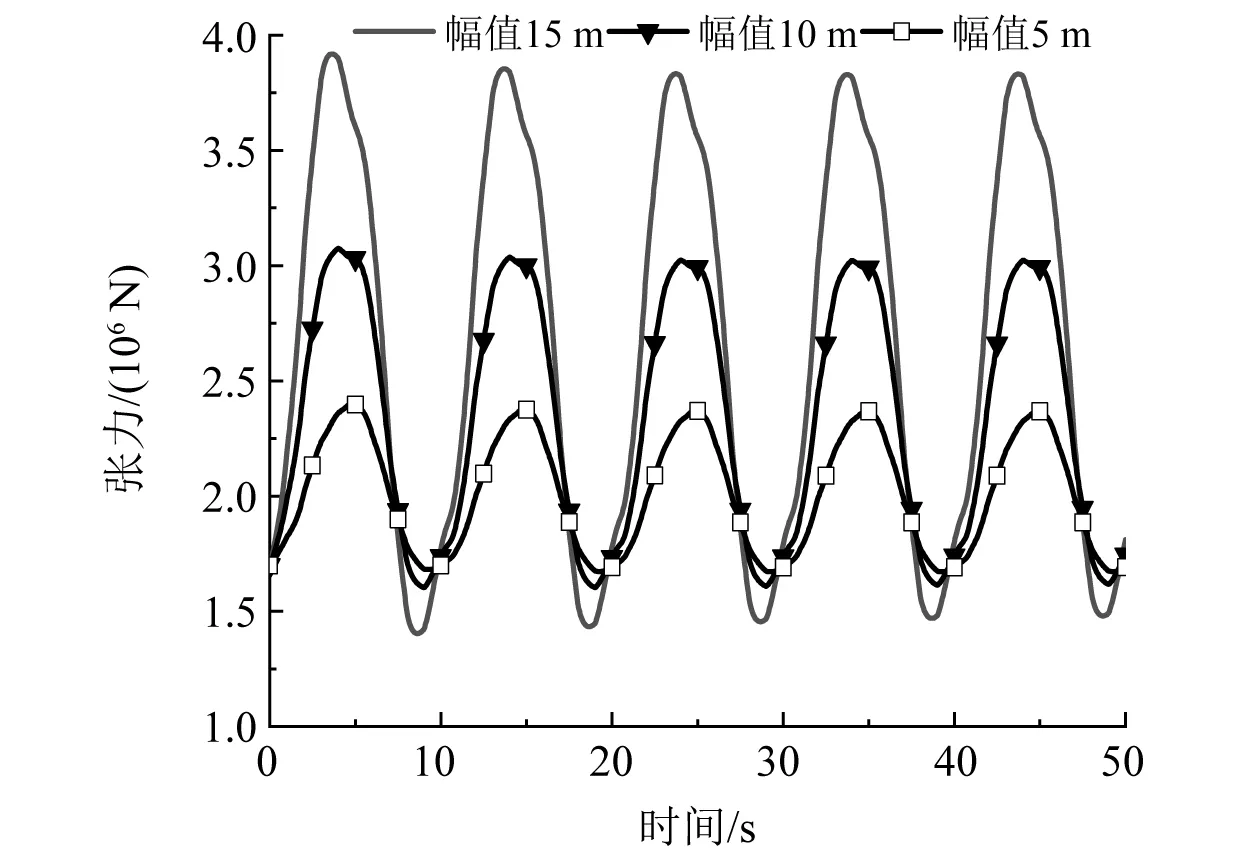
图15 位移幅值对缆索张力的影响
由图15和图16可知,位移幅值的变化仅影响缆索张力和动刚度的数值变化,不会改变这两者的变化趋势(周期和相位角)。在张力方面,缆索位移幅值越大,缆索的张力峰值越大,其中,与幅值为5 m时相比:当幅值为15 m时,缆索张力峰值增加约63.3%;当幅值为10 m时,张力峰值增加约28.1%。在动刚度方面,缆索的位移幅值越大,动刚度整体数值越小,动刚度峰值处变化不大,动刚度谷值的下降最明显。

图16 位移幅值对缆索动刚度的影响
3.5.2 外激励周期的影响
保持位移幅值x0=10 m不变,分别取周期T为10 s、20 s、30 s。计算结果如图17和图18所示。
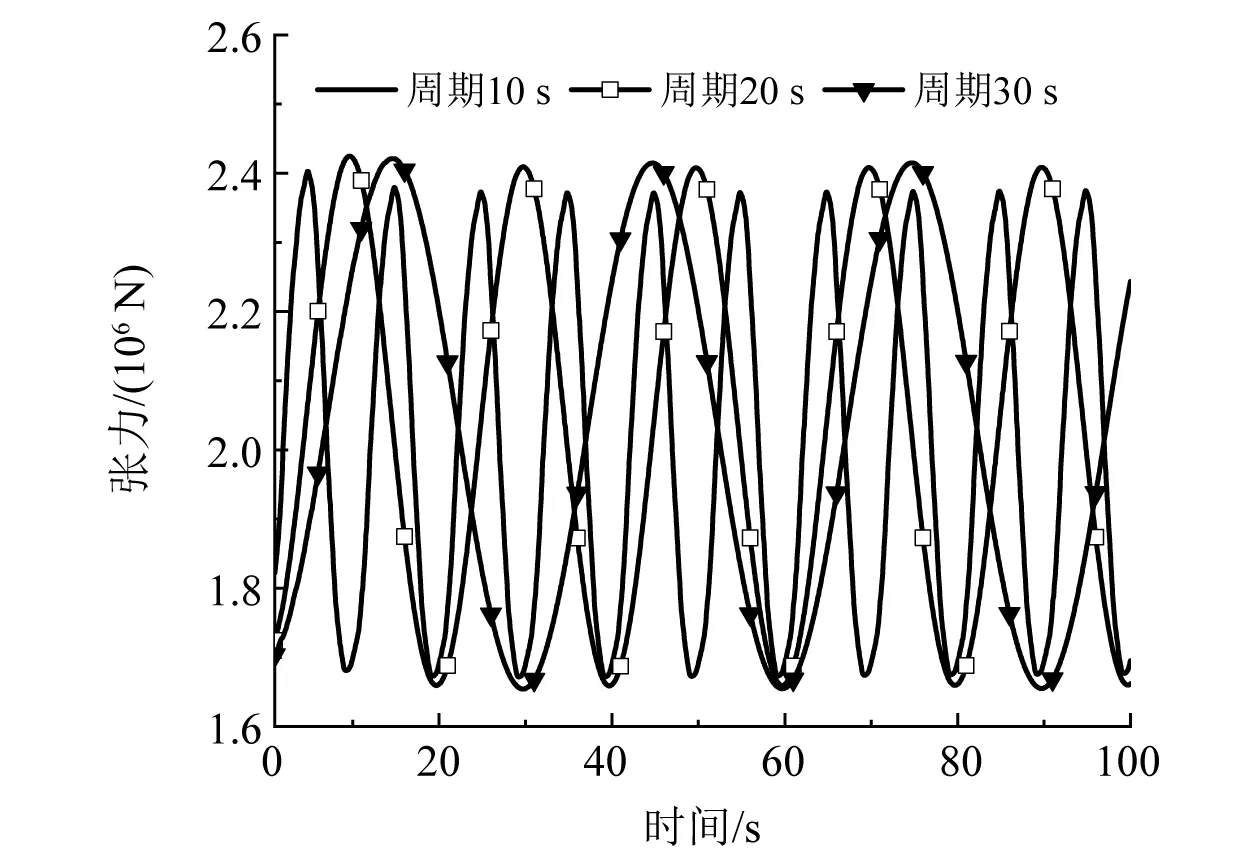
图17 位移周期对缆索张力的影响

图18 位移周期对缆索动刚度的影响
由图17和图18可知,外激励位移周期的变化主要影响缆索张力和动刚度的周期,对两者的数值变化几乎没有影响。在3种周期下,缆索的张力均在1 700~2 400 kN波动,动刚度数值均在14.2~16.3波动。缆索张力的周期始终与外激励位移周期一致,缆索动刚度的周期也会随着位移周期的增大而增大。
4 结 论
简要介绍Abaqus的AQUA模块和UMAT子程序,并阐述这些模块的使用方法;接着介绍所选用的算例及在Abaqus中计算的要点和注意事项;最后,针对具体的算例进行分析,在只考虑缆索拉伸作用的情况下,分别分析动刚度、自重、海流力等不同因素对缆索动力特性的影响,并得出以下结论:
(1) 在考虑缆索动刚度后,计算出的张力结果远大于静刚度情况,引入缆索动刚度非常有必要。
(2) 缆索首尾端的张力并不相同,尾端的张力比首端大,且尾端张力变化稍微滞后于首端。传统张力算法中认为整根缆张力一致是不准确的。
(3) 缆索自重对张力和动刚度有显著影响,自重作用使缆索尾端张力大于首端张力,缆索的自重在张力计算时不能忽略。
(4) 海流力的作用对张力和动刚度有一定的影响,流速对张力和动刚度的影响基本呈线性,海流的作用在张力计算中不能忽略。
(5) 缆索首端位移外激励幅值和周期的变化对张力和动刚度有明显影响:位移幅值的变化主要影响张力和动刚度的数值,幅值越大,张力峰值越大;周期变化主要影响张力和动刚度的周期,张力周期始终与位移周期一致,动刚度周期随着位移周期的增大而增大。

