基于DNN的半潜式平台系统稳定性预测模型

李至立， 却立勇， 刘兴惠

(山东纬横数据科技有限公司， 山东 烟台 264003)

0 引 言

半潜式钻井平台是重要的海洋工程装备[1-2]，往往作业于深海区，时刻面对着恶劣多变的海洋环境，平台系统运行稳定性受到挑战，故障警报信号频发[3-7]。平台系统组成非常复杂，信号点位众多，难以追踪平台系统运行不稳定的诱发因素。机器学习、深度学习等人工智能算法基于大数据可进行复杂的关联映射，比如构建平台系统能否稳定运行与其重要影响因素间的关联模型。本文将平台系统是否发出警报信号作为系统是否稳定的标志，研究平台系统能否稳定运行的重要影响因素，基于若干重要因素采用机器学习、深度学习算法构建平台系统稳定性预测模型。

1 平台系统稳定性关联因素

大型装备故障发生的征兆主要与电压状态有关[8]。采用发电机功率、配电盘各类负载的功率、配电盘各类负载的电压、配电盘各类负载的电流、推进器功率、风速等信号数据作为平台系统能否稳定运行的影响因素。

1.1 平台系统稳定性各影响因素的数据预处理

收集半潜式平台某年5月1日—5月31日上述信号点位的瞬时数据与警报信号数据，将各指标数据中的负值作为异常值设为空值，将毫秒级数据取均值转换为秒级数据。

平台共有8台发电机，但每一时刻只有部分发电机在工作，因此对每一时刻取所有发电机功率的均值作为这一时刻的发电机工作功率，并将其作为建模特征。同理，对每一时刻取8台推进器功率的均值作为这一时刻的推进器工作功率，并将其作为建模特征。配电盘各类负载的功率、电压与电流采用相同的方法得到对应的配电盘综合负载功率、综合负载电压与综合负载电流，将其作为建模特征。将处于同时刻的发电机功率、配电盘综合负载功率、配电盘综合负载电压、配电盘综合负载电流、推进器功率与风速数据作为样本数据，同时剔除空值及离群值所在的样本。将与警报信号处于同时刻的样本输出标记为1，无警报信号的样本输出标记为0。

1.2 平台系统稳定性各影响因素的探索性数据分析

分别以符号DG_power、Thr_power、fzI、fzU、fzW、windspeed代表特征发电机功率、推进器功率、配电盘综合负载电流、配电盘综合负载电压、配电盘综合负载功率和风速，分析特征间的相关性。采用Spearman相关因数，特征相关因数如表1所示。

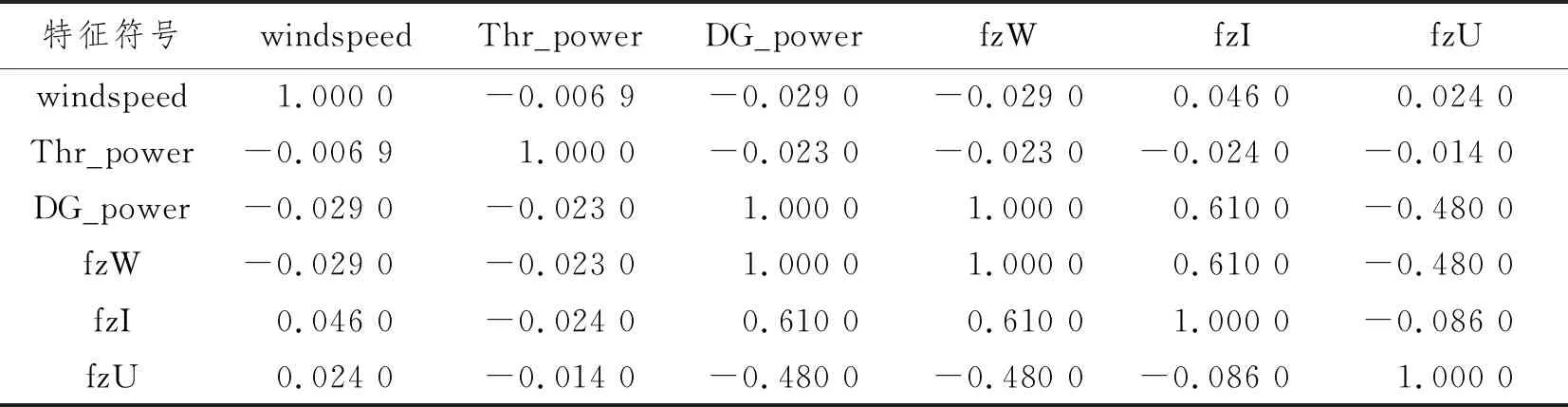
表1 特征相关因数

由表1可知，发电机功率与配电盘综合负载功率呈完全强相关性，可剔除其中一个，与配电盘综合负载电流、配电盘综合负载电压呈中等相关性。

1.3 基于随机森林的特征重要性排序

采用随机森林(Random Forest，RF)对特征重要性进行排序。RF是一种利用Bagging思想，将多个分类回归树(Classification and Regression Tree, CART)决策树作为弱学习器组合为一个强学习器的集成算法，具有良好的抗过拟合能力和较高的准确性，在训练过程中能够识别特征间的相互影响并得出重要性排序。6个特征重要性排序结果如图1所示。

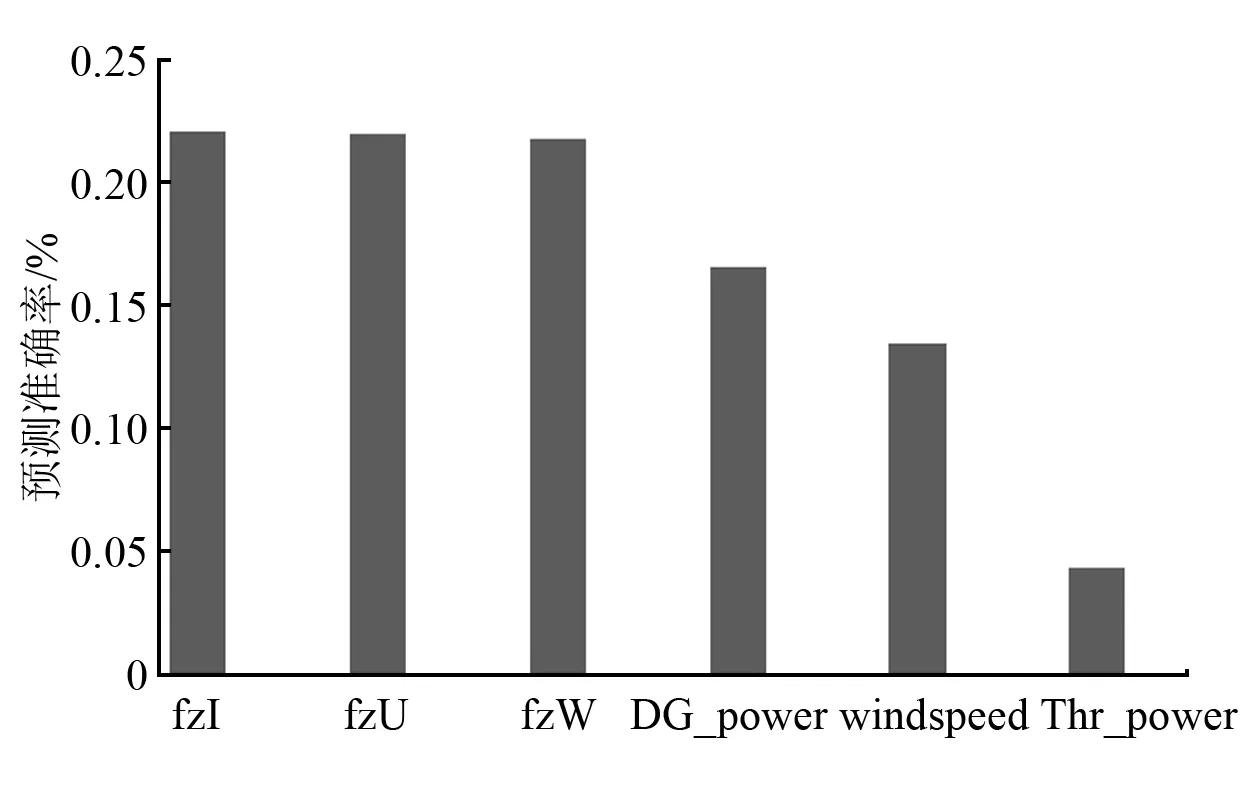
图1 特征重要性柱形图

由图1可知，6个因素对系统稳定性均有一定程度的影响，但配电盘综合负载电流、配电盘综合负载电压、配电盘综合负载功率是系统稳定性的主要影响因素，其次是发电机功率、风速和推进器功率，其中推进器功率重要性最低，可以剔除。

综上所述，配电盘综合负载的功率、电压、电流，发电机功率和风速是决定平台系统能否稳定运行的主要因素，为了保证平台系统的稳定运行，应更关注配电盘各种负载和发电机的运行状态以及防范大风大浪恶劣天气。

2 构建基于DNN的平台系统稳定性预测模型

选择风速、配电盘综合负载功率、配电盘综合负载电流和配电盘综合负载电压作为模型的输入特征。共收集样本476 823个，其中类别1为7 505个，类别0为469 318个，可看成类别不平衡二分类问题。针对类别数量不平衡问题，现有的解决方法可以分为预处理方法、代价敏感方法、算法中心方法和混合方法等4种[9-11]，常用的处理方法包括预处理方法中的采样法与代价敏感方法中的权重法。由于不同类别样本数量差距过大且类别1样本数相对输入特征数足够多，因此采用下采样方式使数据集类别平衡，得到15 012个样本，然后分别采用深度神经网络(Deep Neural Network，DNN)与逻辑回归(Logistics Regression，LR)模型、K近邻查询(K-Nearest Neighbor query，KNN)、支持向量机(Support Vector Machine，SVM)、朴素贝叶斯模型(Naive Bayesian Model，NBM)等传统机器学习算法构建平台系统稳定性预测模型并比较其预测效果。

2.1 DNN基本原理

多层神经网络是一种基于感知机的扩展。如图2所示，感知机的结构由输入、输入的权重、激活函数和输出等4部分组成，将输入值与其对应权重的乘积进行求和，并将该和值作为激活函数的输入，不同的激活函数将会得到不同的输出。

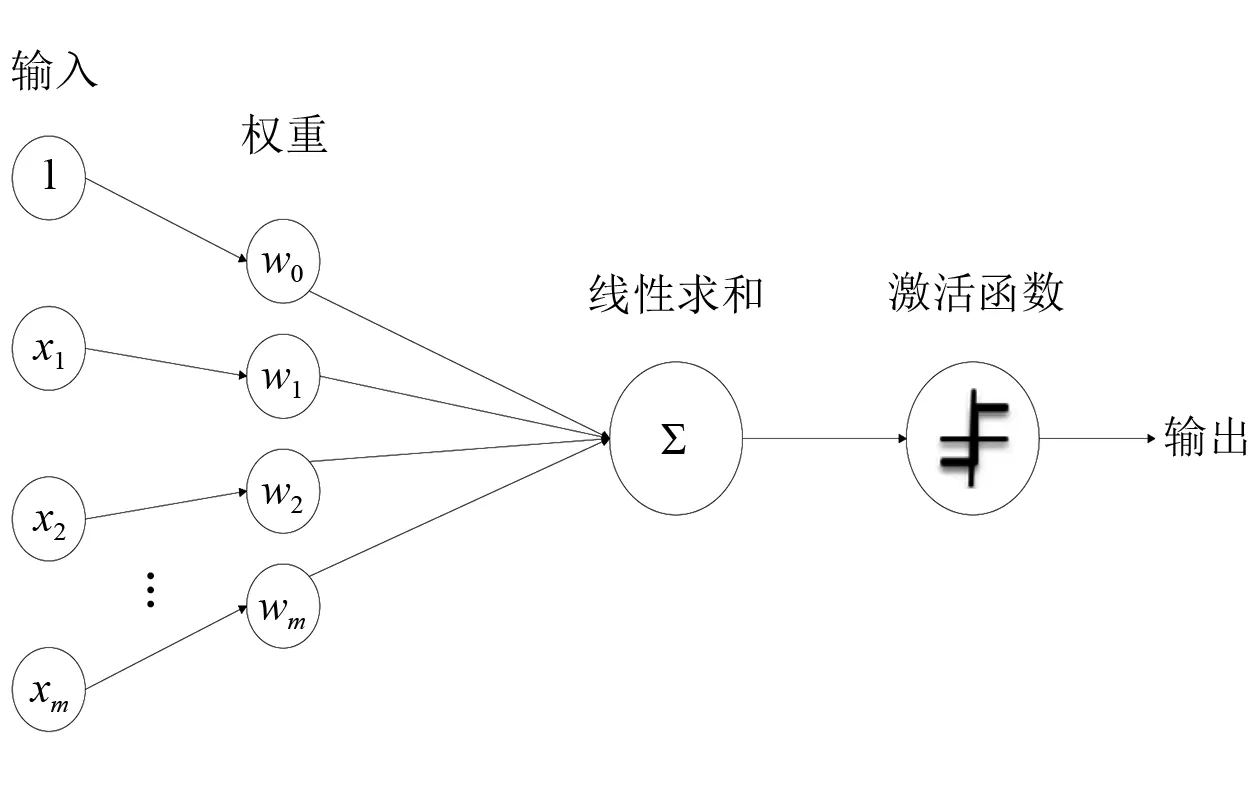
注：x1,x2,…,xm为输入；w0,w1,…,wm为输入的权重；m为输入的数量

在感知机中间增加多层隐藏层，即可得到如图3 所示的多层神经网络。

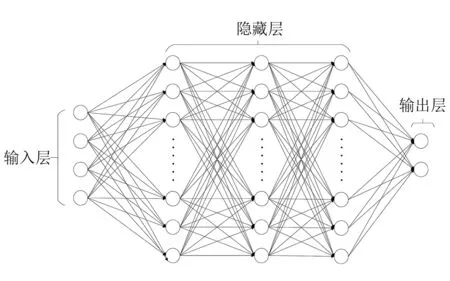
图3 多层神经网络

多层神经网络中神经元的计算方式为

z=∑wixi+b

(1)

式中：z为神经元的值；wi为输入的权重；xi为输入；b为偏置值。同时，为了增强神经网络的表达能力，引入非线性函数(tanh)作为激励函数，计算式为

(2)

结合反向传播(Back Propagation，BP)算法能够实现对高维抽象特征的提取，在平台系统稳定性预测问题上实现高精度的分类及拟合效果。由此可知，DNN依靠多层的神经网络结构和非线性激活函数能较好地拟合平台系统稳定性各影响因素与其之间复杂的非线性映射关系。

2.2 DNN模型构建与评估

对样本数据进行归一化后，固定随机种子将数据集划分为训练集与测试集，测试集比例为20%，用于评估模型，为了防止过拟合将训练集进一步划分出20%作为验证集，同时采用曲线下面积(Area Under Curve，AUC)与准确率作为模型的评估指标。

2.2.1 DNN隐藏层节点数的确定

固定神经网络隐藏层层数为1，通过比较神经网络在采用不同隐藏层节点数的情况下网络经过1 000 次迭代后的验证集Loss的大小来确定合适的隐藏层节点数。试验结果如图4所示。

图4 不同隐藏层节点数单隐藏层神经网络经过1 000次迭代后的验证集Loss值

由图4可知，当隐藏层节点数为14时网络经过1 000次迭代收敛后验证集Loss值损失最小，因此选择隐藏层节点数为14。

2.2.2 DNN隐藏层层数的确定

固定隐藏层节点数为14，通过比较神经网络在采用不同隐藏层层数的情况下网络经过1 000次迭代后验证集Loss值的大小来确定合适的隐藏层层数。试验结果如图5所示。

图5 不同隐藏层层数神经网络经过1 000次迭代后的验证集Loss值

由图5可知，当隐藏层层数为3时，神经网络经过1 000次迭代收敛后的验证集Loss值最小，因此DNN隐藏层层数为3。最终确定DNN拓扑网络结构为4-14-14-14-2，即4层神经网络结构，输入层节点数为4，输出层节点数为2，3层隐藏层的神经元节点数均为14。网络结构如图6所示。

图6 DNN拓扑网络结构

2.2.3 DNN隐藏层激活函数的确定

不同的隐藏层激活函数会给神经网络带来不同的拟合效果，常用的隐藏层激活函数有Sigmoid、Tanh、ReLU和其他变种等，通过比较DNN在分别采用Sigmoid、tanh、ReLU等3种不同的隐藏层激活函数时网络经过1 000次迭代收敛后验证集Loss值的大小来选择合适的激活函数。结果如图7所示。

图7 采用不同隐藏层激活函数的DNN训练效果

由图7可知，虽然网络训练前期ReLU激活函数表现较好，但后期tanh激活函数能够使验证集Loss值收敛至更低，训练效果更好，因此DNN隐藏层采用tanh激活函数更合适。

2.2.4 DNN的训练与验证

在确定DNN拓扑网络结构和隐藏层激活函数之后，确定DNN的输出层激活函数为Softmax，损失函数为交叉熵，优化算法采用Adam，学习率为0.01，网络参数初始化方式采用Pytorch默认的kaiming_normal。网络训练迭代2 000步后训练集Loss值稳定在0.10，验证集Loss值稳定在0.12，网络收敛。网络训练迭代过程如图8所示。

由图8可知，在网络训练迭代2 000步后训练集和验证集Loss值都收敛至0.1，AUC都稳定在0.98，网络得到了较好的训练，泛化能力较强，可以用来预测。采用测试集对该模型进行评估，预测测试集的AUC为0.983，准确率为96.7%。

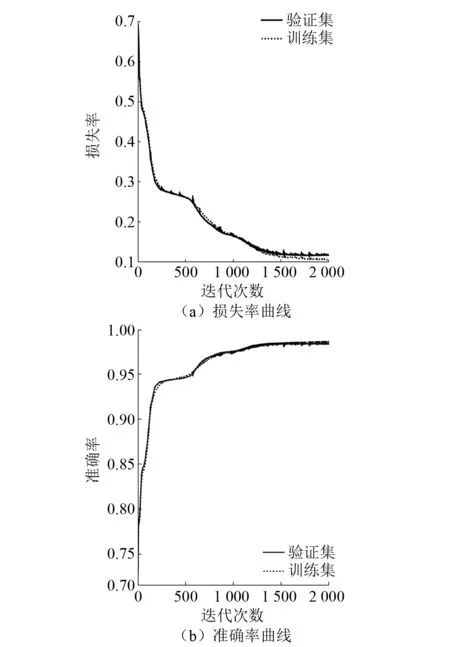
图8 DNN迭代收敛曲线

3 DNN与传统机器学习模型预测效果对比

调用Sklearn库的train_test_split API并采用相同的随机种子以便产生相同的训练集与测试集来训练与评估LR、KNN、SVM、NBM等机器学习模型。DNN与传统机器学习模型预测测试集的评估指标AUC与准确率结果对比如图9所示。

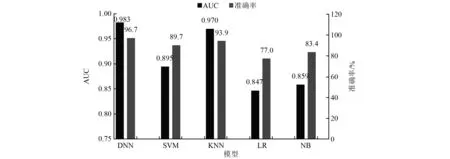
图9 DNN与传统机器学习模型预测测试集的评估指标对比

由图9可知：DNN预测测试集的AUC为0.983，比其他机器学习模型的AUC提高1.3%～16.1%；DNN预测测试集的准确率为96.7%，比其他机器学习模型的准确率提高3.0%～25.6%。因此，采用DNN构建平台系统稳定性预测模型比传统机器学习算法具有更好的拟合效果和泛化能力。

4 结 论

采用半潜式平台工作信号点位数据集研究影响平台系统运行稳定性的重要因素，研究结果表明，配电盘综合负载的功率、电压、电流，发电机功率和风速是影响平台系统运行稳定性的主要因素，也是平台系统产生报警信号的主要触发因素，因此为了保证平台系统的稳定运行，应确保配电盘各种负载的工作状态稳定并且防范大风大浪等恶劣天气。在此基础上，提出基于DNN的平台系统稳定性预测模型，经过测试集评估，该模型的AUC较LR、KNN、SVM、NBM等传统机器学习模型提高1.3%～16.1%，准确率提高3.0%～25.6%，表明DNN模型具有较好的拟合能力和泛化能力。