密度非均匀分布纬编针织物的变形预测及仿真

汝 欣，朱婉珍，史伟民，彭来湖,3

(1.浙江理工大学 机械与自动控制学院，浙江 杭州 310018；2.浙江理工大学 浙江省现代纺织装备技术重点实验室，浙江 杭州 310018；3.浙江理工大学龙港研究院有限公司，浙江 温州 325802)

为满足针织物的设计样式和功能的多样化需求，一件纬编针织物成品往往是由不同密度(横密、纵密)的纬编组织结合而成。如针织护膝、针织防晒袖等贴身衣物，需将其设计成密度非均匀变化的样式来适应人肢体粗细不均的特点。当织物的密度分布不均匀时，织物成品的线圈并非是保持理想形态，而是会发生一定程度的变形。近几年关于纬编针织物变形仿真问题，国内学者主要研究的是线圈级别的变形：沙莎等[1-2]研究了在纬编基本组织中分别引入单个浮线、集圈和移圈线圈单元时线圈发生的变形；雷惠等[3]通过在织物中分别引入不同类型的线圈来研究它们对与其在同一横列的线圈高度的影响，没有考虑对纵行线圈尺寸的影响；国外一些学者关注到了织物的整体变形，Vajiha等[4]针对单双面纬平针织物，提出了一种基于弹簧-质点模型的模拟针织物卷边的方法，仿真效果逼真；Karmon等[5]提出了针对织物整体变形及补偿的织物仿真系统的构想，但是没有给出具体的实现方式。现有纬编针织物CAD变形仿真技术缺少针对密度非均匀分布的纬编针织物的变形研究。

本文以密度非均匀分布的纬编针织物为研究对象，提出一种确定密度非均匀分布的织物弹簧-质点模型初始态的方法，基于二维Peirce线圈模型并结合织物圈距、圈高选取控制顶点建立NURBS线圈模型和质点-控制点关联式，最终实现变形织物的二维仿真模拟，为密度非均匀分布的纬编针织物的变形研究提供解决思路。

1 织物变形预测总体方案

本文基于纬编针织物密度非均匀分布的设计图，对密度非均匀分布的纬编针织物变形预测及仿真方法进行研究。图1示出2种密度的织物组织结合时织物变形研究的图形变化过程。

图1 织物变形模拟过程Fig.1 Simulation process of fabric deformation.(a) Fabric density distribution ；(b) Initial state of spring-mass model of fabric;(c) Mesh deformation diagram of fabric;(d) Loop-mesh model ;(e) Deformation simulation of fabric with non-uniform density distribution;(f) Physical picture of a fabric with non-uniform density distribution

图2示出主要研究流程，具体步骤如下：1)将织物的织物密度分布图转换成相应的织物密度矩阵。密度非均匀分布的纬编针织织物的设计图(后文简称为织物密度分布图)是在织物结构意匠图的基础上结合织物密度改进而来,在织物密度分布图中仅以颜色来区分不同密度的组织，其中，每种密度的组织均由相同结构和大小的线圈组合而成。为便于说明，本文示例中的线圈结构均为成圈。图1(a)示出织物密度分布图，表示的是由 2种密度的织物组织拼接而成的织物，其中黑色部分代表密度大的织物组织，浅灰色部分代表密度稍小的织物组织。

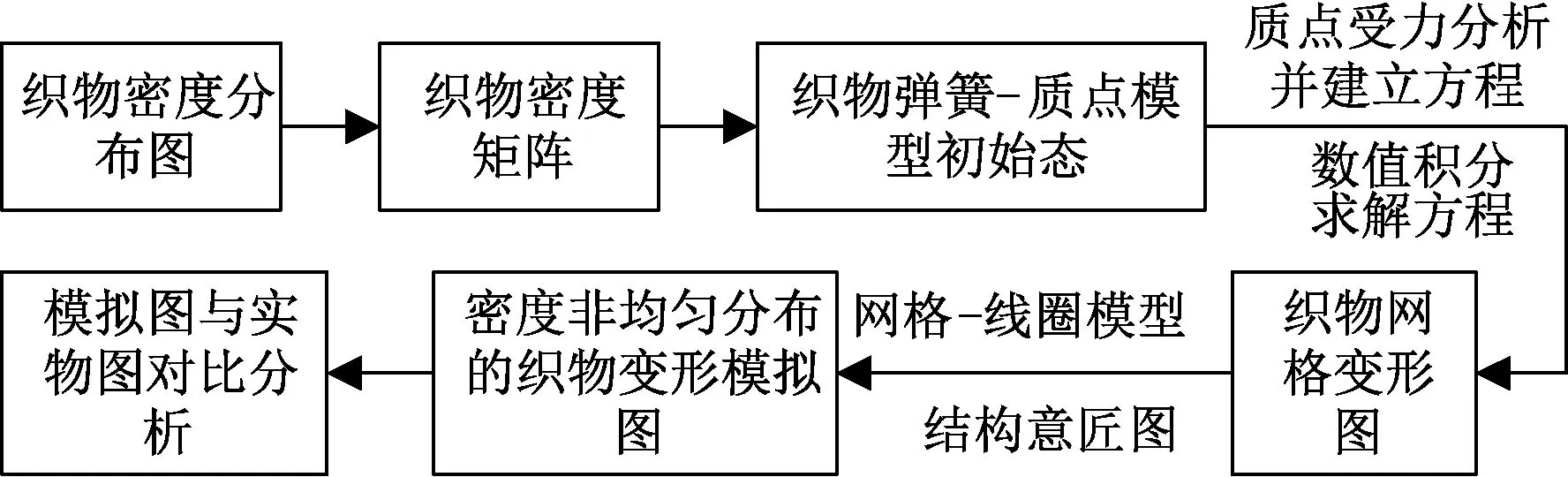
图2 主要研究流程Fig.2 Main research process

2)从织物密度矩阵解析织物尺寸、位置等信息，确定织物弹簧-质点模型初始态。如图1(b)所示为与图1(a)所示的织物密度分布图对应的织物弹簧-质点模型初始态。

3)在织物弹簧-质点模型初始态的基础上结合力学分析计算出质点受力偏移后新的位置，生成网格变形图。图1(c)为据图1(b)生成的织物网格变形图。

4)在织物网格变形图基础上建立曲线线圈模型，形成带有曲线线圈的织物变形模拟图。建立图1(d) 所示网格-线圈模型，再根据织物结构意匠图来确定每个网格单元代表的线圈结构，实现如图1(e) 所示的带有曲线线圈的织物变形模拟。

5)将图1(e)所示织物变形模拟图与实际样品图进行比对，分析仿真效果的可靠性。

2 织物网格变形研究

由织物密度分布图确定织物初始状态的弹簧-质点模型；在此基础上运用胡克定律和牛顿第二定律建立微分方程，采用Verlet数值积分法求解方程得到质点在力的作用下新的位置，形成网格变形图。

2.1 织物弹簧-质点模型的建立与求解

建立织物的弹簧-质点模型，即将织物离散成一群排列有序的质点，质点之间由弹簧(质量忽略不计)连接。在织物的弹簧-质点模型中，连接水平和竖直方向的质点的弹簧为结构弹簧；连接矩形单元格对角线方向质点的弹簧为剪切弹簧；第3种弹簧为弯曲弹簧[6]，其弹簧系数较小，本文不考虑弯曲弹簧。通过控制质点的坐标位置来控制线圈的形态，最终实现整个织物的变形模拟。

为便于选取质点，本文先将织物进行简化，平面的纬编针织物表面线圈呈纵、横向排列分布，据此将织物以线圈为单位按照纵、横2个方向进行网格划分，将织物简化成二维网格[7]，线圈单元简化成了四边形单元格，如图3(b)所示。在织物的二维网格图中，二维网格纵、横方向的单元格个数对应织物纵、横方向的针数，矩形单元格的高B、宽A对应着理想线圈的圈高、圈距。

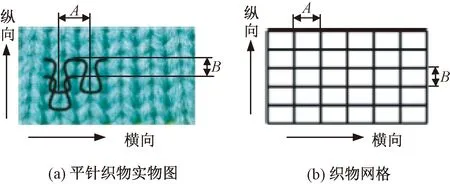
图3 织物的二维网格Fig.3 Two-dimensional mesh of fabric.(a) Physical picture of weft plain fabric;(b) Fabric mesh

选取织物二维网格图中单元格顶点作为质点，单元格的宽、高为结构弹簧的2种长度，单元格对角线长度为剪切弹簧的长度；横列数m、纵行数n的针织物对应(m+1)×(n+1)个质点构成的弹簧-质点模型。图4示出弹簧-质点模型的示意图。

图4 弹簧-质点模型Fig.4 Spring-mass model

2.1.1 织物弹簧-质点模型初始态的确定

为方便计算机读取，需将织物密度分布图进行数字化处理：将织物的线圈以矩阵元素的形式存储在矩阵中，矩阵中1个矩阵元素表示织物中对应位置上的1个线圈，定义该矩阵为织物密度矩阵ρ。

(1)

式中：i=1,2,…,m;j=1,2,…,n；ρi，j=k表示织物中第i行第j列的类型为k的线圈，k=1,2,…;类型相同的线圈其所在织物组织的密度相同，将其所在组织也称为组织k。矩阵行数m、列数n分别表示织物线圈的横列数和纵行数。

在织物的网格图中，不同密度的织物组织表现为不同大小的矩形单元格。根据织物密度矩阵ρ，确定织物第i行第j列的线圈k值，根据线圈的k值来确定该线圈所处组织的圈距和圈高，进一步确定质点的坐标。说明密度均匀时根据线圈的类型值k,可确定质点坐标的方法。织物第i行第j列的线圈类型为k,其对应的圈高和圈距分别为B、A,则该线圈的4个质点坐标值如图5所示。

图5 单个线圈坐标与尺寸图Fig.5 Coordinate and dimensional diagram of individual loop

现以图1(a)所示的织物密度分布图为例，说明其对应的密度非均匀分布织物的初始状态的弹簧-质点模型建立过程。

图1对应的织物密度矩阵ρ为

(2)

其中,

图1(a)所示织物是由2种密度的组织拼接而成，这2种密度分别为组织1、组织2(中间密集部分)。先假定所有组织的矩形单元格的宽度和高度都为组织1的宽、高来赋予质点坐标值初值，形成如图6(a)所示网格；接着根据织物密度矩阵确定织物中组织2的线圈在织物中的位置，将组织2的实际大小所占据的区域(图6(b)小方格组成部分)和组织2被当成组织1所占据的区域(图6(b)虚线方框框选)按照几何中心重合的方式重新确定组织2各质点的坐标位置，形成图6(b)所示的织物初始状态的弹簧-质点模型。

图6 织物的弹簧-质点模型Fig.6 Spring-mass model of fabric.(a) Fabric mesh;(b) Initial state of spring-mass model of fabric

从图6(b)可以看到处于组织过渡处的线圈已经不再是规则的四边形，该四边形的4个顶点处的质点处于非平衡受力状态，模拟了由于密度不同导致的2种密度过渡处织物受力不均衡的状态。

2.1.2 质点受力分析及微分方程的建立与求解

质点的位移遵循牛顿第二定律：

F=amm

(3)

式中：F为质点受到的内力与外力的矢量和，本文不考虑外力的影响，因此这里的F即为弹簧的弹力(结构弹簧力和剪切弹簧力);mm为质点质量；a为质点加速度。由于采用的是理想弹簧，不考虑阻尼力，弹簧力F遵循胡克定律：

F=-KΔx

(4)

式中：K为质点间弹簧的弹簧系数；Δx为弹簧的变形量。图7为质点受力分析图。

图7 质点受力分析图Fig.7 Force analysis diagram of mass

假设当前质点为Mm,Mn是与Mm连接在一根弹簧上的质点，则当前质点所受的弹簧力合力为

(5)

式中：n=1,2,…，8；Km,n为连接当前质点Mm与Mn之间弹簧的弹簧劲度系数；xm和xn分别为当前质点Mm和质点Mn在t时刻的位置矢量；lm,n为弹簧原长。

Verlet积分[8-11]方法计算速度快，精度高，简单稳定，故选用Verlet积分方法进行微分方程的数值求解。

(6)

将式(5)代入式(6)得：

x(t+Δt)=2x(t)-x(t-Δt)+

(7)

式中：x(t)为当前质点在t时刻的位置矢量；Δt为迭代时间步长；F(t)为当前质点所受到的合力。上式表明，由质点当前时刻t和前一时刻的位置矢量和受力情况可预测该质点下一时刻的位置。

2.2 织物网格变形实现

求解弹簧-质点模型获得质点在一定时间后的位置，图1(b)示出初始状态的弹簧-质点模型在力的作用下最终形成图1(c)所示的织物网格变形图。在图1(b)示出的织物二维网格变形图中，内层密度大的组织其变形趋势是向周围扩散的，外层密度小的组织有往中间收缩的趋势，且其变形程度比紧密组织的稍大，符合密度大的组织更加稳固的实际情况。整个织物中变形最大的部分是发生在2个组织交接处，越远离组织交接处，线圈变形程度越小甚至没有变形。织物网格变形图代表了织物的变形趋势。

3 线圈-网格模型

为使织物外观模拟更具真实感，采用NURBS曲线描述线圈形态；建立二维网格质点与线圈曲线控制点之间的关联式，定义其为质点-控制顶点关联式。由质点坐标和质点-控制顶点关联式计算出对应曲线的控制顶点坐标，由控制顶点生成相应的NURBS曲线线圈，最终实现对整个织物的线圈建模。

3.1 NURBS线圈模型

3.1.1 NURBS曲线

在针织物的线圈仿真模型中，NURBS曲线[12]的形态可通过控制顶点实现局部调控，因此不会因单个控制顶点的改变引起整条曲线形态都发生改变，形态更加可控。基于此，本文采用NURBS曲线进行线圈形态模拟。

k次非均匀有理B样条曲线(k次NURBS)表达式[13]为

(8)

式中：Pi为控制顶点，构成控制多边形；ωi>0为权因子，确定控制(顶)点的权值，其值越大，曲线越接近相应的控制点，这里取ωi=1，k=3,u=[u0,u1,…,un+k+1]为节点矢量，节点矢量首末取四重节点即u0=u1=u2=u3=0，un+1=un+2=un+3=un+4=1，内节点u4,u5,…,un采用里森费尔德方法[14]确定；Ni，k(u)为定义于非均匀控制矢量上的k次B样条基函数。

3.1.2 选取线圈模型控制顶点

本文在如图8(a)所示二维Peirce线圈模型[15]基础上选取线圈的NURBS曲线控制顶点，在矩形单元格中选取图8所示10个点Pi(i= 0,1,…，9)，作为三次NURBS曲线线圈的控制顶点，形成如图8(b) 所示的的NURBS线圈。其中，虚线部分为控制多边形，实线部分为1个NURBS曲线线圈，P0P1P2、P7P8P9段控制线圈的沉降弧形态，P2P3、P6P7段控制圈干形态，P3P4、P5P6段控制针编弧形态。

图9示出了纵向线圈之间相互串套关系，其中黑色实线代表当前线圈，Mj(j=1,2,3,4)为质点，Pi(i=0,…,9)为NURBS曲线(控制顶点)。控制顶点Pi(i= 0,1,…，9)的坐标为

图9 线圈纵向串套关系示意图Fig.9 Diagram of longitudinal cascade relationship of loops

pi=kx,iAx+ky,iBy,i∈[0,9]

(9)

式中：x，y分别为x、y方向的单位向量；矩形网格宽度A为圈距；高度B为圈高；kx,i,ky,i分别为当前控制点与A，B的比例系数，其取值详见表1，其中系数大于1的点在由Mj(j=1,2,3,4)构成的矩形单元格的外部，小于1的点在矩形单元格的内部。

3.2 质点-控制顶点关联式

建立质点与控制顶点的数学关系式[1,15]，由质点-控制顶点关联式和质点坐标就可计算出控制点坐标，将控制顶点代入式(8)生成相应的NURBS曲线线圈，如图10所示。控制点用来控制线圈的几何形状，质点控制四边形的形状，当质点受力偏移，四边形发生变形；相应的NURBS曲线线圈也发生变形,如图10(b)所示。每个单元格的4个质点关联1个线圈的10个控制顶点。

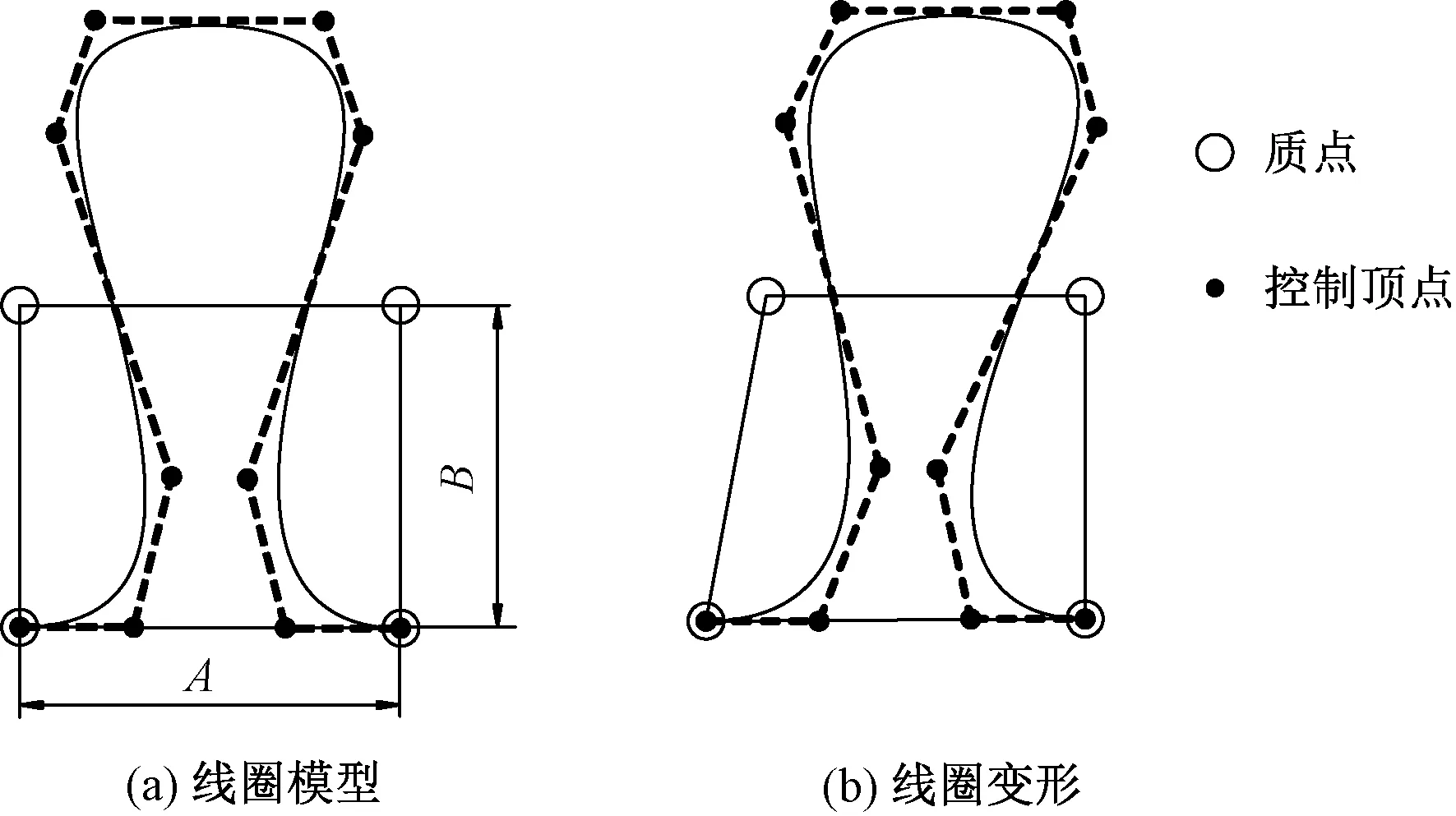
图10 线圈-网格模型Fig.10 Loop-mesh model.(a) Ideal style of loop;(b) Deformed loop

结合表1，将控制顶点Pi(i=0,…,9)用质点Mj(j=1,2,3,4)线性表示,用矩阵相乘形式表示即

表1 线圈控制点比例系数取值表Tab.1 Value of scale factor of control point of loop

(10)

式中：P=[P0,P1，…,P9]；M=[M1,M2,M3,M4]。

按行、按列遍历网格变形图中每一个单元格，依次用NURBS曲线线圈取代每个四边形单元格，最终形成整个织物的变形仿真图，如图1(e)所示，其为图1(c)所示网格变形图对应的变密度非均匀变化的织物变形模拟图。

4 实验与织物仿真效果分析

4.1 织物样品

设计实验，将真实织物与其对应的仿真图对比，分析仿真结果的可靠性。

为减少干扰因素，所有样品采用相同的纱线原料：39.37 tex×7腈纶，样品由慈星电脑横机 CE2-60S 编织而成，实验设计了如图11所示2种样式的织物样品。其中图11(a)所示样品由3种密度的平针组织组成，从上往下分别为平针组织1(紫色)、平针组织2(蓝色)、平针组织3(绿色)；图11(b) 示出的样品由2种密度的平针组织组成，从里到外分别是平针组织2(蓝色)、平针组织3(绿色)。样品具体参数详见表2。

图11 样品实物图Fig.11 Physical picture of sample.(a) Sample 1;(b) Sample 2

表2 织物规格参数表Tab.2 Fabric specification parameters

4.2 计算机织物仿真及效果分析

使用javascript进行数据处理和计算，使用SVG进行图形绘制，对样品1、2进行仿真,仿真的部分信息见表3。仿真图如图12所示。

图12 样品仿真图Fig.12 Simulation diagram of sample.(a) Sample 1；(b) Sample 2

表3 计算机织物仿真的部分信息表Tab.3 Partial information of fabric simulation on computer

计算机织物仿真算法流程如下。

输入：织物各组织的横列数、纵行数、圈距、圈高等参数。

输出：织物线圈仿真图。

步骤1：初始化织物弹簧质点模型的质点坐标。

步骤2：遍历所有质点，对质点进行受力分析。

步骤3：建立质点的力学微分方程，并使用数值方法求解方程，得到质点在力的作用下一个时间步长的位移，更新质点位置。

步骤4：重复步骤2、3，当所有质点相比上一次迭代，其位移量不大于设定的极限值时，停止迭代。

步骤5：将质点位置代入质点-控制顶点关联式，得到控制顶点位置。

步骤6：根据控制顶点确定NURBS曲线，显示织物仿真图。

对照图11样品实物图与图12中相应的仿真图分析知，仿真图与实物图变形趋势是一致的，整体尺寸也基本保持一致。变形程度最大的线圈主要集中在不同密度的组织交接处，远离组织交接处的线圈变形程度逐渐变小,且织物外轮廓处变形和实际织物的卷边也保持一致。

5 结束语

根据织物密度分布图建立织物弹簧-质点模型，对模型中质点进行受力分析并建立微分方程，采用Verlet数值积分求解方程，形成织物网格变形图，在此基础上结合NURBS曲线线圈模型，形成密度非均匀分布纬编针织物仿真图，对比仿真图与实际样品，变形趋势高度一致。研究为密度非均匀分布的纬编针织物的变形研究提供了一种解决思路，对设计者预测密度非均匀分布的纬编针织物成品最终外观形态有一定的参考价值。但本文织物组织的组合样式比较少，另外涉及到织物中大量线圈的变形问题时，仿真模拟的计算效率也是值得关注的问题，本文仿真的计算效率还有待提升。

FZXB