高中数学核心素养下的问题式教学案例

刘俊蓉 杨秋 明庆

摘要：现高中数学的六大核心素养：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析，这六大核心素养既相互独立，又相互交融，共同构成了学生的数学综合能力。是学生学习数学的基本思维品质、关键能力以及情感、态度、价值观的综合体现。需要教师在教学过程中积极探索合适的教学方法，培养学生的核心素养。在当前时代背景下，学生核心素养的培养受到了高度的重视，如何在常态教学中植入六大核心素养的培养，是教师教学中的重点、也是教学的难点。核心素养的形成过程就是学生的数学思维的建立和数学综合能力的培养过程。所以常态教学课中教学路径的探究就成了我们的一个重要课题，问题式教学路径是老师们在日常教学中采用的一种常用的教学方法。

关键词：高中数学、核心素养、培养、教学路径、问题式

一、教学案例

（一）授课对象与方法

本节课的授课对象是四川省广安友谊中学高一学生。该校是一所省级示范校，一本升学率可达到50%，学生基础在广安市相对较好。授课内容是普通高中教科书《数学》必修 第一册（A版）第三章3.1.1《函数概念》第一课时。主要采用问题串式教学法。

（二）教学设计

1.新知导入

初中的定义中，函数是刻画变量之间对应关系的数学模型和工具.

例：正方形的周長 l与边长 x的对应关系

思考：（1）l是x的函数吗？

x∈R  y=1，y是 x的函数吗？

2.新知探究

问题1  某“复兴号”高速列车加速到350 km/h后保持匀速运行半小时.

思考：（1）列车行进的路程S与运行时间t 的关系是什么？

（2）有人说：“这趟列车加速到350 km/h后，运行1 h就前进了350 km.”你认为这个说法正确吗？

问题2   某电气维修公司要求工人每周工作至少1天，至多不超过6天.如果公司确定的工资标准是每人每天350元，而且每周付一次工资.

思考： 工资w（单位：元） 与工作天数d 的关系是什么？

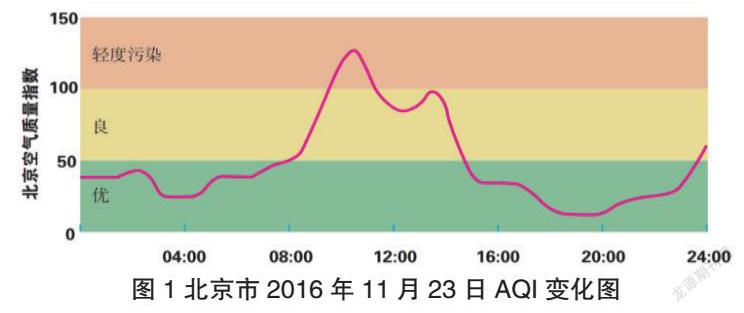
问题3  如图1是北京市2016年11月23日的空气质量指数（Air Quality Index，简称AQI）变化图.

图1 北京市2016年11月23日AQI变化图

探究 ：请你仿照问题1和问题2，用两个集合和一种关系描述问题3.

问题4 由上述三个问题抽象出来的数量关系有哪些共同特征？

① 都包含两个非空数集，用A、B来表示;

② 都有一个对应关系;

③ 对于数集A中的任意一个数 x，按照对应关系，在数集B中都有唯一确定的数 y 和它对应.

对应关系除了我们熟悉的函数表达式，还可以是图像、表格等。

为了表示方便，我们引进符号 f 统一表示对应关系。

函数概念：  一般地，设A，B是非空的实数集，如果对于集合A中的任意一个数 x，按照某种确定的对应关系 f，在集合B 中都有唯一确定的数 y和它对应，那么就称 f：A→B为从集合A到集合B的一个函数，记作y=f（x），x∈A.

其中，x叫作自变量，x的取值范围A叫作函数的定义域;与x的值相对应的 y值叫作函数值，函数值的集合{f（x）|x∈A}叫作函数的值域.

概念剖析：（1）构成函数的三要素

（2）值域与集合B的关系

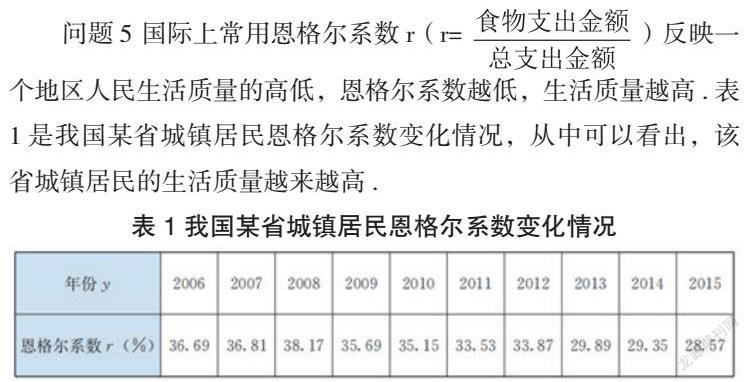
问题5 国际上常用恩格尔系数r（r=）反映一个地区人民生活质量的高低，恩格尔系数越低，生活质量越高.表1是我国某省城镇居民恩格尔系数变化情况，从中可以看出，该省城镇居民的生活质量越来越高.

表1 我国某省城镇居民恩格尔系数变化情况

探究 ：按表1给出的对应关系，恩格尔系数r 是年份y 的函数吗？为什么？

3.典例分析

抢答题：（1）判断下列对应关系是否是函数.

①A={平面M内的三角形}，B={平面M内的圆}，f：画三角形的外接圆;

②A=R，B={x|x>0}，f：x→y=|x|;

③A={x|-1≤x≤1}，B={1}，f：x→y=1.

④下列图形中不能构成函数y=f（x），x∈A.的图像的是（ ）

抢答题： （2）下列哪些函数与 y = x 表示同一函数？

①; ②; ③; ④

思考： y=2x2-x+1  与  y=2t2-t+1 是否为同一函数？

二、案例分析

问题式教学：是以提出问题、分析问题、解决问题为线索，并把这一线索始终贯穿整个教学过程。也就是教师先设计好问题，学生带着问题进入课堂，通过理解问题，讨论问题，针对性地解决问题。这种教学法操作方便，适合高中生，实践效果良好。在问题式教学中问题的质量是关键，问题之间要有逻辑关系，要切中要害，引起学生的兴趣。

本节课在短短的40分钟课堂内，要让学生经历函数定义发展史上百年的探究历程，学生不可能独立完成。这需要教师用材料铺好一条路，要了解学情，并对学生的疑问做好预测，难度大的地方搭好梯子。本节课以学生为主体，教师引导教学原则来设计，着重解决了学生的几个疑问：

（一）引发认知冲突

初中定义中，函数是刻画变量之间对应关系的数学模型和工具.

例如，正方形的周长 l与边长 x的对应关系   l=4x.

思考：（1）l是x的函数吗？

（2）x∈R  y=1，y是 x的函数吗？

通过回忆旧知，引出困惑

用快剪辑制作短视频《函数概念的发展史》，激发学生的学习冲动和学习热情.

（二）概念的生成

高一学生的抽象概括能力还很薄弱，这使得用集合语言刻画函数概念很有难度。如果直接归纳定义，学生会失去刚刚燃起的探究欲望。所以选择从情景问题1入手，引导学生关注时间t的变化范围，跳出问题情境，抽象出数量关系，得出：两个非空数集A、B及其之间的对应关系;紧接着，抛出情景问题2，用问题串引领学生完成实例2的分析，在分析过程中重点让学生体会分析情境，辅助学生抽象出数量关系并进一步理解数量关系中的任意性、存在性、唯一性;接下来的情景问题3，学生根据图像描述对应关系有困难，特别是在值域不能完全确定时，通过引入一个较大范用的集合，使函数值“落入其中”，这是学生经验中不具备的，由老师规范表述，进一步强化数量关系中的任意性、存在性、唯一性。

学生通过归纳三个情景问题的共同特征，体会数学抽象过程，概括出用集合与对应语言刻画的一般性函数概念.让学生进行归纳、概括、抽象出函数概念，并以此培养学生的数学“抽象素养”这一难点。

通过创设情境，形成概念。尤其注重了概念的自然生成。从特殊到一般，揭示数学通常的发现过程，给学生“数学创造”的体验。这种引入概念的方式自然而又易于学生接受和形成概念

（三）概念的理解

引导学生从函数概念的内涵、要素的归纳过程，关键词的理解等角度进行小结，进一步加深对函数槪念的理解。

利用已有概念，判断情境问题5是否构成函数，并体会以表格形式呈现的对应关系。

（四）概念的应用

新课引入，概念生成，到这个时候已经上课快30分钟，学生注意力，精神状态都略显不足。此时，我以倒计时抢答题的形式增加课堂乐趣，巩固新知。例1判断下列对应关系是否是函数，进一步从任意性、存在性、唯一性这三性理解函数概念。其中③A={x|-1≤x≤1}，B={1}，f：x→y=1.回应了引入中（2）x∈R  y=1，y是 x的函數吗？

例2 和相应的思考，有效的帮助学生进一步理解函数三要素，课外拓展设计以开放式角度训练思维。

三、案例效果

本节课是一堂高效课堂。高效课堂是高效型课堂和高效性课堂的简称，是教育教学效率或效果达成了相当高的目标。具体而言是指在有效课堂的基础上，完成了教学任务，达成了教学目标，效果较好并且取得了教育教学的较高影响力和社会效益的课堂，高效课堂是有效课堂的最高境界，高校课堂基于高效教学，与教学的设计和教师的能力有很大的关系。

这节课的设计思路清晰，课堂气氛活跃，以游戏抢答的方式寓教于乐。问题的设置多样化，有教是事先预设的问题链，也有学生主动提出的问题，同时还有问题的开放性，提升学生的思维。根据问题学生的学习目标明确，效果突出，很好地激发了学生的内在动力。40分钟，学生理解并掌握了函数的内涵，本质。通过课堂习题反馈情况看，这节课起到较好的教学效果，大多数学生能独立、正确地完成.

参考文献：

[1]中华人民共和国教育部制定.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2018.

[2]章建跃.第三章“函数的概念与性质”教材介绍与教学建议[J].中学数学教学参考（上旬），2019（28）：17-24.

[3]王克亮.高中数学教学“问题驱动”的探索与实践[M].苏州：苏州大学出版社，2017.