微观轨迹数据驱动的交织区换道概率分布模型

刘 兵，王锦锐，谢济铭，陈金宏，段国忠，叶保权，侯效伟，彭 博

（1.云南省交通投资建设集团有限公司，昆明650103，中国； 2.昆明理工大学 交通工程学院，昆明650500，中国；3.重庆交通大学 交通运输学院，重庆 400074）

交织区内不同流向车辆的换道行为导致其成为常见的交通瓶颈[1]。因此，立足微观层面，针对交织区的车辆换道行为，开展宏观特征分析与微观风险建模，是探明交织区运行机理缓解交通拥堵的基本前提。

宏观特征分析研究包括换道行为管理与通行效率的提升。SUN Shicheng 等[2]建立了考虑多种换道管理方案的元胞自动机仿真模型，提出不同几何和交通条件下的最优换道管理方案；AN Xu 等[3]仿真模拟了不同的车道分配方案下的交织区运行效率，得到交织区车道分配策略。

微观风险建模主要利用高精度数据对交织区车辆换道行为展开研究。张兰芳等[4]依托自然驾驶实验数据，构建了快速路出口影响区换道风险模型；张雪榆等[5]通过采集交织区自然驾驶数据，分析交织区车辆行驶轨迹特征、速度特征等微观驾驶行为；MA Yanli 等[6]基于势能场理论构建了交织区车辆主动换道仿真模型；韩皓等[7]基于深度学习理论进行交织区车辆强制性换道轨迹的预测；HAO Wei 等[8]建立了一个异质交通流环境下的高速公路交织区车辆强制换道模型，验证了未来自动驾驶车辆（connected and automated vehicle, CAV）的换道安全识别性；谢济铭等[9]结合车辆轨迹数据与机器学习方法，提出了一种多车道交织区的潜在风险判别与冲突预测方法。

可以看出，微观特性研究可进一步揭示交织区车辆运行规律与特性，但对数据精度、算法复杂度要求较高，既有研究较少利用高精度微观轨迹数据构建车辆行驶行为仿真模型。因此，本文基于无人机所摄高空视频提取高精度微观轨迹数据，构建交织区换道决策模型，对交织区车辆换道行为规律仿真分析，进行车辆换道行为机理研究。

1 数据采集

本文主要研究快速路交织区车辆换道的变化特性与微观机理，数据采集交织区选址具有以下特性：1）典型的城市快速路主线同侧型交织区，该交织区车道数量较多、交织距离较短；2） 交织区在工作日高峰期具有明显常发性拥堵，调查时段内无特殊交通事件；3）路段及其周边物理结构条件良好，天气晴好时可进行视频航拍检测。在图1 中方框表示当前跟踪车辆，线条为跟踪车辆的运行轨迹。同时，通过现场实测，获取交织区的基本参数。

图1 数据调查与提取

在经典核相关滤波（kernelized correlation filters，KCF）车辆跟踪算法的基础上[10]，针对交织区的复杂环境进行算法优化，并基于高空视频提取交织区行经车辆换道信息。考虑到交织区车道划分不均、线形多变，仅判别横向位移和速度难以准确提取换道信息，本文使用9 阶多项式分别拟合路缘线、车辆轨迹，采用虚拟线圈检测器记录换道时刻的轨迹连续片段，提取到的换道信息包括车辆换道次数、位置及方向等，检测了车辆行经交织影响区域的完整微观轨迹2 912 条。结果表明，车辆轨迹拟合优度均值99.10%，路缘线拟合优度均值98.65%，检测结果精度较高，拟合效果较好，可满足提取换道信息数据精度的要求，为模型的参数标定提供了量化依据。

2 换道模型构建

2.1 模型框架

借鉴随机规划问题中的两阶段法理念，构建了一个两阶段协同换道元胞自动机模型，将交织区车辆换道过程划分两层决策阶段：上层决策阶段为战略层和战术层，其中，战略层决策为驾驶人换道动机判别，战术层决策为换道时机选取；下层决策阶段为作业层，即驾驶人根据上层决策结果，执行换道行为。模型框架如图2 所示。

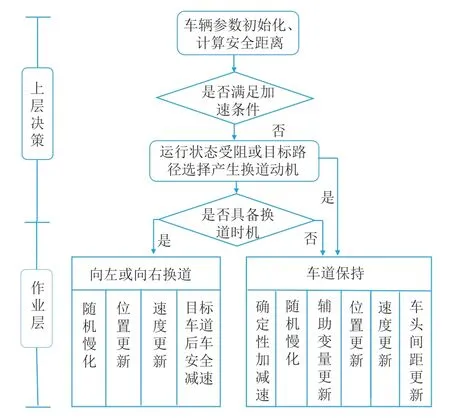
图2 模型框架示意图

2.2 上层换道决策阶段

2.2.1 换道动机

换道动机为驾驶人换道实施前的预判结果。由于交织区几何条件和交通流组成较为复杂，驾驶人需在中上游较短的距离内连续换道，汇入下游目标车流，换道动机错综复杂。因此，本文将换道动机归纳为3 类。

第1 类：换道动机是车辆行驶受阻。为了寻求更快的通行速度与更大的行驶空间，这类换道动机公式为：

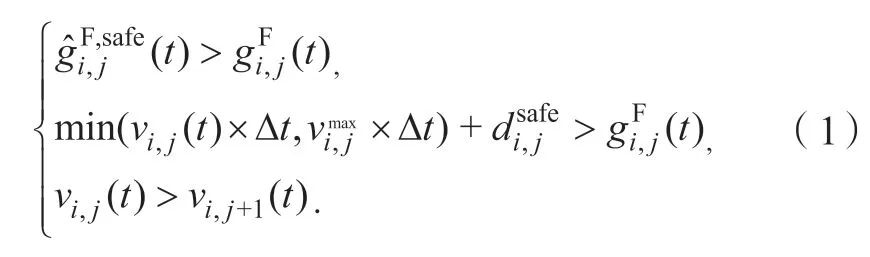
其中：i为车辆的横向位置（车道）；j为车辆的纵向（行驶方向） 位置为行车安全间距阈值

其中，v0为车辆低速行驶阈值。

第3 类：换道动机体现为驾驶员路径选择驱动。本文根据交织区存在路径选择的实际情况，综合考虑车速、间距及汇入汇出比例，判断换道需求，构建车辆路径转换的换道动机为：

then 产生驶入匝道需求；

then 产生汇入主线需求。

其中：ω1为主线向匝道的车辆汇入比；ω2为匝道向主线的车辆汇入比。

2.2.2 换道时机

根据换道间距条件对换道的时机进行判断属于上层决策阶段中的战术层决策。为体现多车道交织区车辆换道时与周边车辆的间距关系，将换道间距条件分为5 种情况，如式（3）—（7） 所示。

其中，条件a） -d）是基于第1 类换道动机下的换道条件，条件e） 是基于第2 类换道动机下的换道条件，第3 类换道动机则体现在车辆在交织区运行的全过程中。这5 种情况换道强度及安全风险均逐渐增加，考虑到驾驶人实际决策时间与安全优先意识，模型逐等级逐时步进行判断，依据驾驶人实际驾驶决策过程，将判断决策时间定义为从驾驶人发现危险信号到松开加速踏板所经过的时间，每次决策间隔Δt时步。当能够满足其中之一即可认为满足换道间距条件。

a） 车辆与目标车道前后车有足够的间距，可保证车辆安全换道：

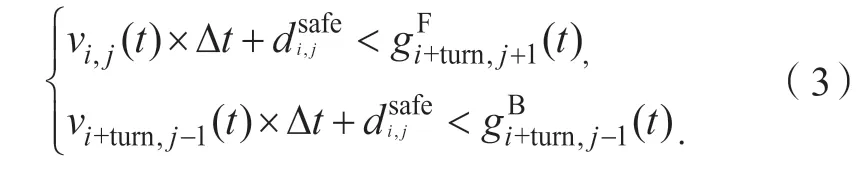
b） 如无法满足上述条件，则t+ Δt时步判断车辆与目标车道后车有足够的间距，但与前车间距较小时，换道时存在本车追尾前车的风险：

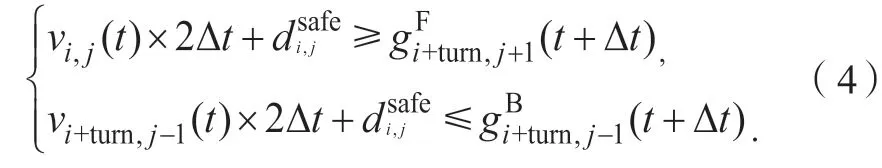
c） 车辆与目标车道前车有足够的间距，但与后车间距较小时，换道时存在后车追尾本车的风险：

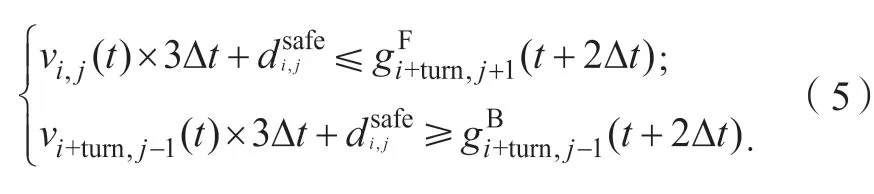
d） 车辆与目标车道前后车辆间距均较小，车辆可能会减速换道，与前后车发生事故的风险较大：

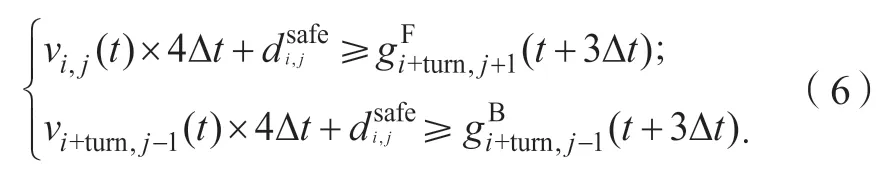
e） 车辆路线不熟悉、前车停车阻碍通行、行驶至交织区末端等情形下，车辆低速甚至停车伺机换道的行为：

当驾驶员有换道动机时，模型首先判断是否满足a～e 换道时机其中之一，条件b） -e）规则换道行为虽冒险，但反映了驾驶员在交织区不同的换道需求、换道利益和安全判断。

一方面在交织区低速环境下，车辆的制动距离与制动时间较短，同时驾驶员精神较集中，时刻紧密关注周边情况，反应时间也较短，一定程度上可保证在苛刻的行驶条件安全运行；另一方面驾驶员在交织区的换道意愿更强烈，部分驾驶员为实现短距离限制下的连续换道，不得不以更冒险的换道行为实施换道。同时，部分车辆的冒险换道行为也会影响到谨慎型驾驶员的驾驶心理，即一部分谨慎型驾驶员受周边车辆冒险行为影响，体现出“效仿”行为，因此交织区换道要更激进一些。

2.3 下层换道执行阶段

2.3.1 换道分布频率函数

通过观测实验视频，发现交织区内车辆相互影响较大，换道难度大，行车风险高。考虑到车辆在交织区存在目标路径选择的问题，提取高峰时段交织区换道信息得出换道频率分布。为了更直观地分析主要参与交织车辆的换道分布，暂不讨论最内侧定向车道的换道规律，对其余4 个车道在交织影响区域的换道位置与次数分布进行了Gaussian 拟合，构建换道分布频率关系式如下：

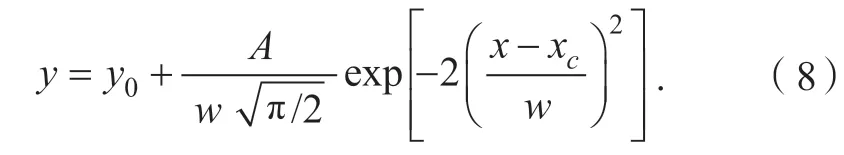
其中：y为交织区换道分布频率，y0为调节换道分布曲线整体上移或下移的参数，xc为调节换道分布左右平移的参数，w为调节换道频率分布宽窄幅度的参数，A为峰面积，各方向系数取值与假设检验结果如表所示，其中，车道3 至车道4、车道4 至车道3 方向为双峰Gaussian 模型。

检验车辆在交织区的换道频率与换道位置之间关系可得，偏度均小于3，峰度均小于10，可认为此关系基本服从正态分布[11]；拟合优度均大于85%，说明换道次数分布的拟合效果较好，模型函数能够准确地反映交织区实际换道分布特性。据此，建立换道概率Gaussian 分布模型H(x)。

其中：Hsingle（x）为单峰分布；Hdouble（x）为双峰分布；a1为函数在纵向偏移量；为峰值极限值为横向偏移量；为分布曲线形状参数；x为车辆位置。

2.3.2 换道分布频率函数标定

作业层阶段主要是执行上层决策的结果。根据上述分析结果，对模型参数进行标定，当车辆(i, j)运行至交织影响区任意车道i时，根据所处位置k和换道方向的不同，对应取不同换道频率分布函数，以向左换道为例，换道分布函数表达式为：其中：b1为调节换道分布曲线整体上移或下移的参数；b2为调节换道分布峰值的参数；b3为调节换道分布左右平移的参数；b4为调节换道频率分布宽窄幅度的参数。

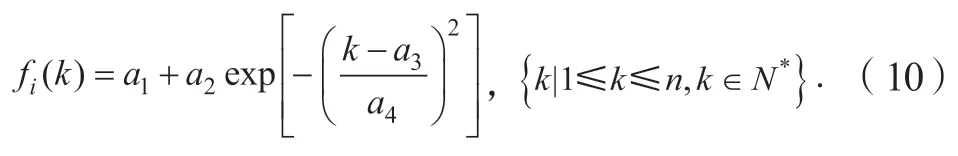
如前所述，由于不同车道不同方向换道的不均衡性，换道分布存在差异，概率调节系数取值相应不同。同时为提升计算机仿真运算效率，将换道概率与元胞位置逐一对应，采用1×j维的矩阵，表示当车辆(i, j)运行至交织影响区车道i、元胞位置k时其换道概率。

综合上述分析，对式（10） 中相关参数进行了标定，车道1 →车道4 车辆换道后，根据不同车道不同方向相应的换道分布存在差异，且符合Gaussian 分布。其中，车道3 和车道4 之间由于存在末端换道，换道频率呈双峰分布，故以双峰模型的形式呈现；车道1只存在向右换道，车道4只存在向左换道，具体换道分布函数如图3 所示。

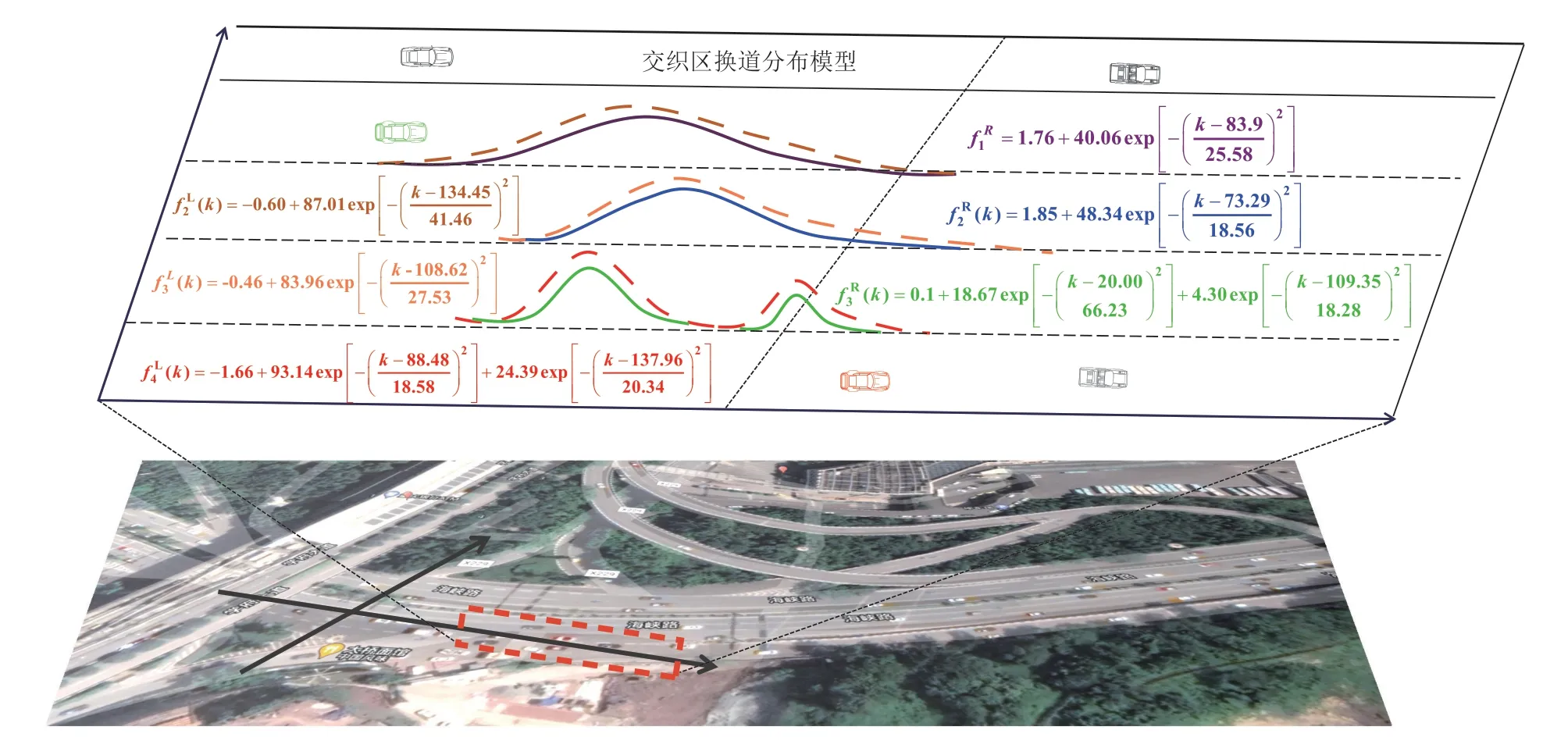
图3 交织区车辆换道分布及函数

3 数值模拟与分析

3.1 仿真设置

经典元胞自动机模型尺寸长度 （lcell）为7.5m，步长（Δt）为1 s， 考虑到它难以体现多车道交织区复杂的换道决策行为，根据实测换道间距分布与驾驶人反应时间[12]，在前述章节基础上细化了模型尺寸lcell= 1 m，Δt= 0.2 s，进行仿真，以更好地描述车辆实际换道行为特征。模型空间初始化参数如表1 所示。

表1 元胞空间参数

3.2 基本图分析

统计交织影响区平均流量、平均密度及平均速度的实测值与元胞空间仿真值，分别计算流量、密度、速度的相对误差，结果表明：对于平均流量、密度和速度，模型相对误差分别为0.7%、1.4%、1.6%，模型运行结果较符合实测数据。绘制元胞空间交织影响区所有车辆全时步平均流量—平均密度、平均流量—平均速度及平均密度—平均速度图，并进行多项式曲线拟合，如图4 所示。

图4a 所示，平均流量—平均密度曲线呈二次抛物线状，随密度的增加，流量呈先增加再平缓后降低的趋势，当密度在[50,70]区间范围时流量变化趋于平缓，流量峰值约为每车道（lane）每h 900 标准车当量(pcu)，即900 pcu / h，与实测值基本相符。

图4b 所示，平均速度—平均密度为线性函数关系，随车流密度的增加，速度随之减小，最终密度集中于[80,100] pcu / km，速度集中于[7.5,17.5] km/h 附近，密度和速度值基本与实测值相符。

图4c 所示，平均速度—平均流量曲线上半部分交通状态不拥挤，随流量的增加，速度相应降低，曲线下半部分交通状态较拥挤，流量减小的同时，速度也相应降低。

流量、密度与速度整体分布较符合Green-shields交通流变化规律，表明模型可较好地模拟和反映交织区交通流特性。

3.3 换道频率分布分析

图5重点展示了交织影响区范围内6 个方向换道频率分布情况对比分析实测和仿真结果。由图5 可知：仿真得出的换道分布与实测变化趋势相近，数据基本相符，较好地展现了车辆在交织区换道过程中出现的聚集换道和末端换道等现象，验证了模型的准确性。

从图5 可以看出：主线驶向匝道的部分车辆会在未进入交织区前提前变更车道，避免无法汇入目标路径车流；不参与交织的部分主线车辆在进入交织区后，倾向于选择换至运行车速更高的内侧车道，这与交织区实际观测运行情况一致。

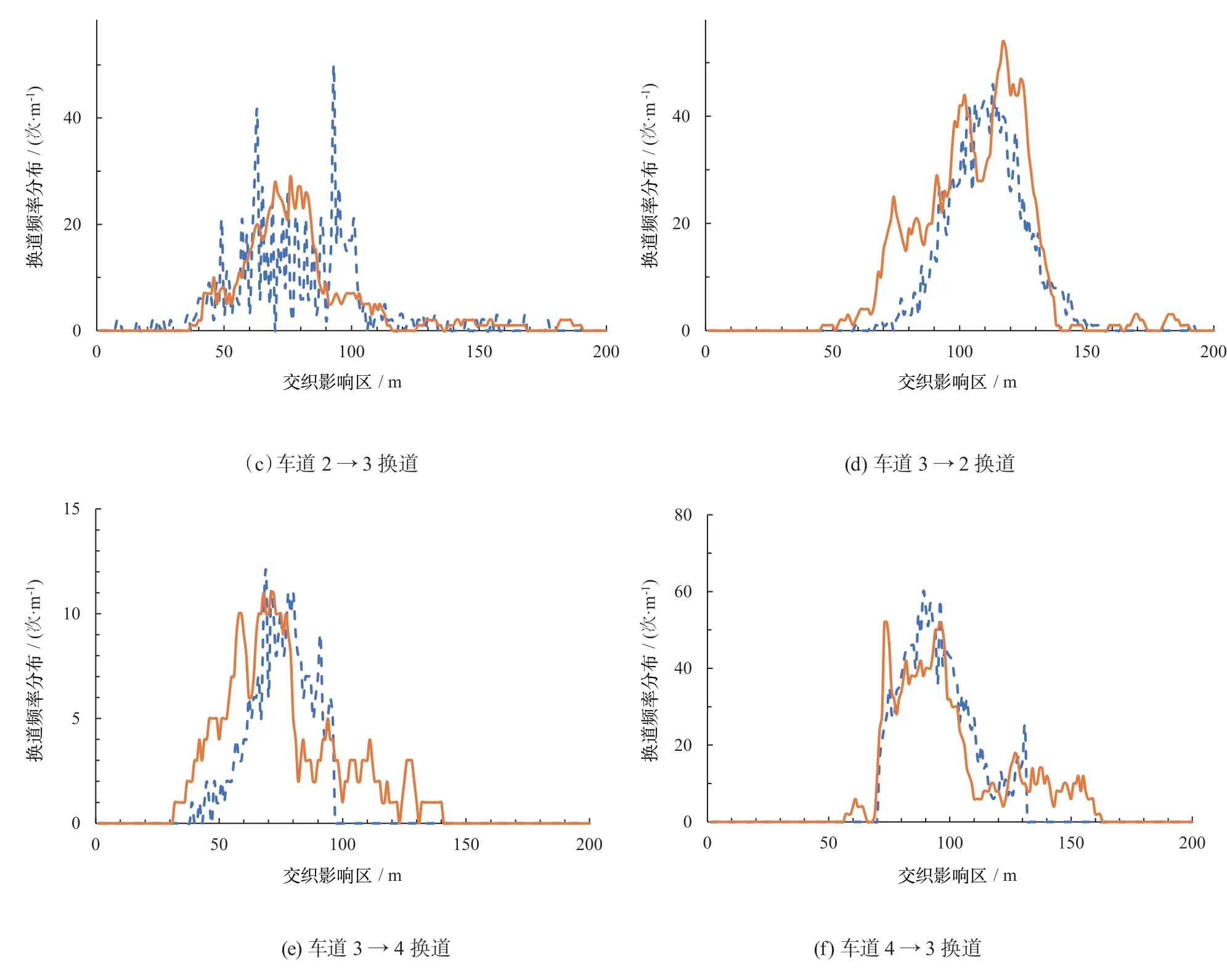
图5 各种换道频率分布

值得注意的是，车道2 →车道1 的换道仿真数据与实测数据之间误差较大，这可能是由于交织区内侧车道车速较快，属于高速车流，外侧车道的低速车流汇入高速车流较为困难，影响因素较多，需在后续研究中对模型进行进一步优化。

可见，在多车道交织区，车辆往往难以进行自由换道，若需要驶离快速路的车辆在进入交织区前未能提前驶入靠右车道，便会选择减速等待换道机会或冒着发生事故的危险强行换道，不仅影响快速路入口的车辆驶入，也对交织区的换道功能造成了严重的损伤。

4 结 论

本研究基于交织区交通流基本特性，引入随机规划问题中的两阶段法理念，将车辆在交织区的换道过程划分为换道判断与换道执行2 个阶段，构建了一种基于换道频率分布的换道决策模型。利用采集到的实际交织区交通流运行数据对模型进行了标定并仿真，仿真结果与实测数据相比，流量、密度、速度的相对误差分别为0.7%、1.4%、1.6%，不同方向换道次数误差为2.97%～22.98%，表明模型可有效刻画交织区车辆微观换道行为特征。智能网联环境下，车路信息将会更易获取、更加及时，在未来的研究中，可以考虑对人工驾驶车辆与网联车辆混行情况下的交织区车辆换道微观特性展开深入细致的研究。