基于DRL 的四轮独立驱动电动车辆的侧向车速估计

郑阳俊，贺 帅，帅志斌,*，李建秋，盖江涛，李 勇，张 颖，李国辉

（1.中国北方车辆研究所，北京100072，中国；2.汽车安全与节能国家重点实验室（清华大学），北京100084，中国）

车辆关键运动状态的测量和估计一直是车辆动力学领域的研究热点[1]。在车辆的平面运动状态中，纵向车速、侧向车速、横摆角速度是影响车辆操控性能和行驶稳定性的关键。量产车上安装的惯性测量单元（inertial measurement unit, IMU）等传感器能够对纵向加速度、侧向加速度、横摆角速度等进行较为精确的测量，纵向车速也可通过车轮转速进行估计，而侧向车速的测量难度较大，难以通过量产车上安装的传感器进行准确的实时测量[2]。虽然车载GPS （全球定位系统，global positioning system）模块能对纵向车速、侧向车速等运动状态进行测量，但受限于地形、天气等因素，通常难以保证持续良好的GPS 卫星信号质量，存在不稳定因素，并且量产车的GPS 模块数据更新速率较低，获取的车速难以用于车辆动力学相关的强实时控制。因此，通过传感器获取的有限的车辆状态信息，对车辆侧向车速或质心侧偏角进行估计，是汽车行业一直以来广泛关注的研究和应用领域。

已有许多围绕车辆侧向车速和质心侧偏角精确估计的研究工作，并形成了行之有效的估计方法[3]，包括：Kalman 滤波器（Kalman filter, KF）及其变种（扩展KF、无迹KF、容积KF、联邦KF 等）、模糊逻辑观测器、神经网络和深度学习等方法。金贤建提出了一种基于双容积KF 的车辆质心速度和质心侧偏角观测方法[4]。樊东升基于联邦KF 实现对车辆速度和路面附着系数的联合估计[5]。肖峰设计了基于无迹KF 的车辆横摆角速度和质心侧偏角估计方法[6]。施树明提出了一种基于模糊逻辑的车辆质心侧偏角估计方法[7]。

除了广泛采用的KF 算法以外，神经网络也被尝试应用于车辆运动状态的实时估计上。张凤娇提出了一种基于深度学习的极限工况下车辆状态估计方法[8]。汪䶮提出了一种基于深度学习的车辆关键状态平行估计方法[9]。Ribeiro 采用时延神经网络实现了对轮胎—路面附着情况的实时估计[10]。

近年来，在车辆控制领域，深度强化学习(deep reinforcement learning, DRL)技术也得到了应用。目前针对DRL 的应用研究主要集中在混合动力车辆的能量管理、自动驾驶车辆的路径规划等领域。HAN Xuefeng 采用double DQN 算法进行混合动力履带车辆的能量管理[11]。李文礼采用深度确定性策略梯度(deep deterministic policy gradient, DDPG)算法实现了车辆自主避撞决策控制[12]。

也有学者利用强化学习方法进行车辆系统的状态估计和参数辨识。高洪森将DRL 与KF 算法相结合，提出了一种锂离子电池SOC（荷电状态，state of charge）估计方法[13]。Kim T. 利用基于模型的强化学习算法进行轮胎参数的辨识，并在此基础上进行路径跟踪控制[14]。WANG Pengyue 利用分布式强化学习算法对智能交通系统中车辆的不确定性进行估计[15]。

本文基于DRL 的范式，结合深度神经网络，设计了一种基于DDPG 算法的四轮独立电驱动车辆侧向车速估计方法。通过对神经网络、奖励函数、训练场景等的合理设计，所训练得到的智能体，可望对车辆侧向车速进行准确的估计。

1 深度强化学习

1.1 问题描述

车辆的侧向车速需要基于车载传感器易于测量的状态量，通过设计专门的状态观测器或估计算法进行计算得到。目前的估计方法主要包括2 类：

1)基于模型的估计方法。如图1a 所示。常规车载传感器易于测量的状态量包括：车辆的纵向加速度ax、侧向加速度ay、横摆角速度γ，各车轮转速ni，方向盘转角δ等。大多数估计方法都是基于上述测量信号，并结合车辆动力学模型设计观测器（如Kalman 滤波器），进行车辆状态的估计。

2)数据驱动的估计方法。即本文所采用的方法，如图1b 所示。基于四轮独立电驱动车辆中易于获取的可测量状态量，在状态量中增加了各车轮转矩Ti，结合深度神经网络的非线性拟合能力和强化学习的高效训练模式，设计并训练出能够对车辆侧向车速进行准确估计的策略。

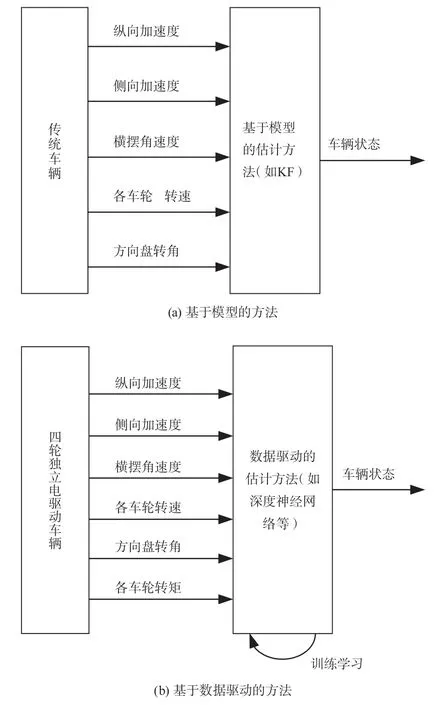
图1 2 种车辆状态估计算法比较

对于四轮独立电驱动车辆，由于其各车轮的输出转矩Ti可以独立、精确地控制，带来了2 方面的影响：

1) 各个车轮的输出转矩能够用来作为状态观测器的输入，更多的可测量信号为状态估计提供了更多的信息和数据源，同时也为估计算法的设计提供了更大的自由度[16]；

2) 由于各车轮转矩的独立控制，导致行驶工况的多样性、复杂性、非线性等特征更加显著，容易超出传统观测模型的适用范围，给基于模型的估计方法带来了新的挑战。

因此，基于数据驱动的估计方法在估计效果上更具潜力。

1.2 深度强化学习

深度强化学习(DRL)是机器学习的一个分支，它一方面基于深度神经网络实现复杂非线性数据关系的拟合，另一方面又采用强化学习的范式对其中的若干个深度神经网络的参数进行训练；因此可以认为是深度学习和强化学习的结合。DRL 的优势在于，其通过探索试错和奖励函数的机制，能够快速地实现神经网络超参数的高效学习和训练优化。

DRL 的基本架构如图2 所示。

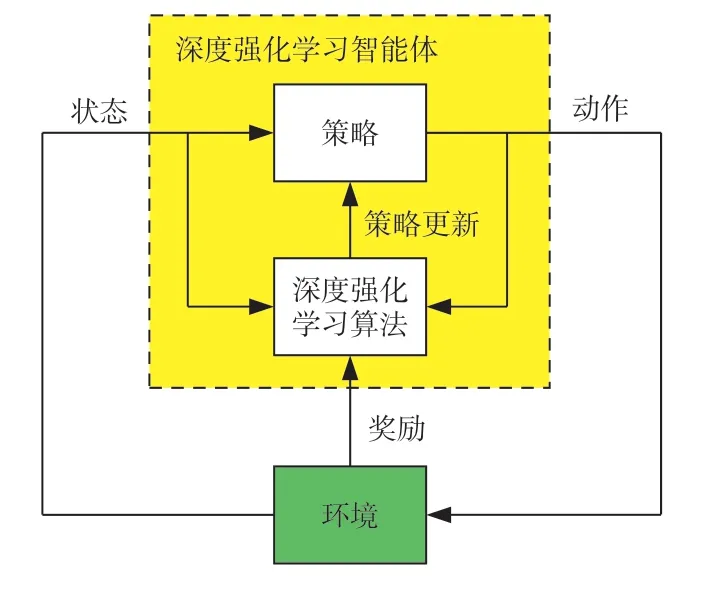
图2 深度强化学习的基本架构

2 基于深度强化学习范式的侧向车速估计方法设计

2.1 基于深度强化学习的侧向车速估计架构

本研究基于DRL 的范式对四轮独立电驱动车辆侧向车速进行估计，其总体架构如图3 所示，主要包括智能体（Agent）和环境（Environment）2 部分。智能体从环境中获得的状态量包括：车辆纵向加速度ax、车辆侧向加速度ay、方向盘转角δ、车辆横摆角速度γ、各车轮转速ni、各车轮的驱动转矩Ti。

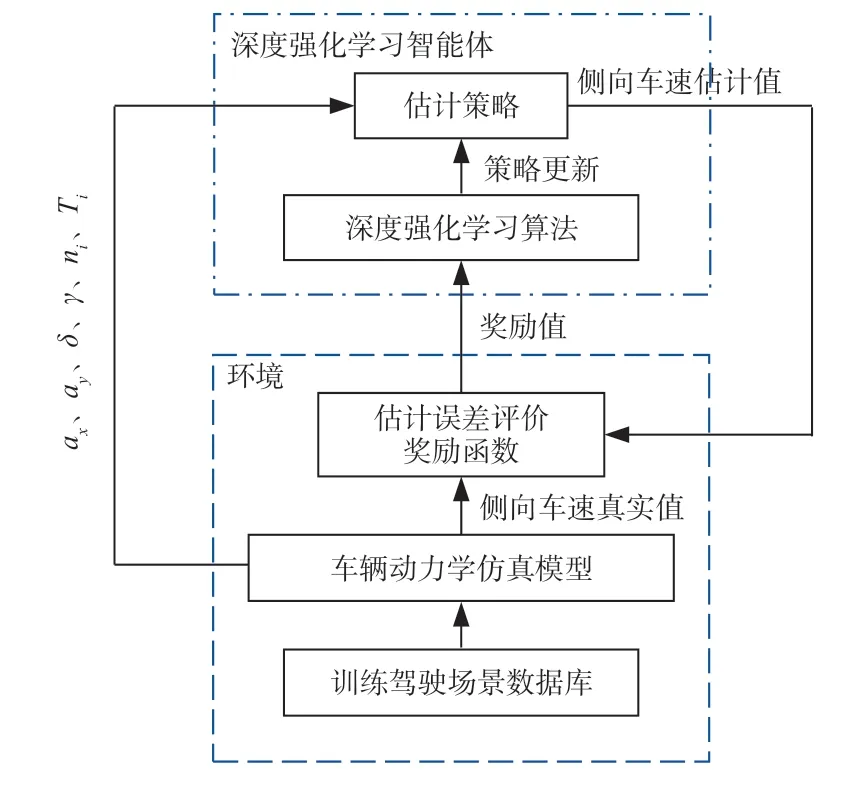
图3 基于深度强化学习范式的侧向车速估计架构

上述车辆状态量也即DRL 中的状态空间，即

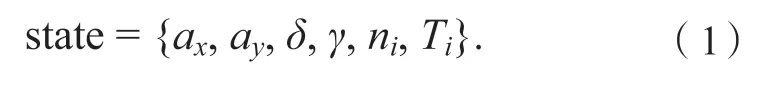
状态的选取主要考虑2 方面因素：能够表征车辆行驶过程中的关键动力学状态；在量产车中通过常规的车载传感器和控制器容易进行测量或直接计算。

“智能体”是用于对侧向车速进行估计的主体，其内部包含估计策略，基于传感器可测量的车辆状态量，通过深度神经网络对车辆的侧向车速进行估计。同时，其内部的深度强化学习算法又能根据输入的可测量状态量、输出的车速估计值、估计误差评价函数所反馈的奖励值对估计策略进行训练和更新，使其估计精度得到不断提高。

“环境”的主体是用于提供数据驱动的车辆动力学模型（或装有专业测量设备的试验样车），其主要作用是通过大量的行驶场景（模型仿真或实车测试）为智能体提供足够的训练数据来源，并将其输出的车速估计值与仿真模型内部输出的（或专业设备测量得到的）车速真实值进行对比，生成奖励值反馈给智能体，供其进行策略的学习和更新。

“动作”(action)在深度强化学习的控制应用中是指智能体根据输入状态和内部策略，对外界环境做出的反应。对于本研究中的状态估计问题，智能体的对外输出动作则是其对车辆侧向车速的估计值vˆv，因此对动作的定义为

2.2 深度强化学习DRL 算法选取

近年来，已衍生出一些适合不同应用场景需求的DRL算法，如：深度Q网络 （deepQnetwork，DQN）算法、近端策略优化（proximal policy optimization，PPO）算法、深度确定性策略梯度（deep deterministic policy gradient, DDPG）算法等。本研究中的状态和动作都是连续变量，因此选取DDPG 算法作为DRL 智能体的算法。

DDPG 算法的核心是Actor 网络和Critic 网络[17]。Actor 网络负责基于当前的状态空间输入计算出当前的动作，并输出至环境；Critic 网络根据状态和动作进行Q值的计算；基于Critic 网络计算的Q值和环境反馈的奖励值，对Actor 网络和Critic 网络的参数进行调整和更新。DDPG 算法的主体架构如图4 所示。

图4 DDPG 算法的主体架构框图

在实际应用的DDPG 算法中，Actor 网络和Critic网络各有2 个，分别为当前网络和目标网络，此外，DDPG 算法还借鉴了DQN 算法的经验回放功能，通过使用经验池可以提高训练效果。

2.3 Actor 网络与Critic 网络设计

深度神经网络的设计是决定深度强化学习效果的关键。本研究采用DDPG 算法构建深度强化学习智能体，需要对其中的Actor 网络和Critic 网络进行设计，如图5 所示。

图5 Actor 网络与Critic 网络设计

输入层：在Actor 网络和Critic 网络的输入层，首先需要对输入的变量值进行归一化处理，以提高网络的计算精度和训练效率。由于网络的输入都是车辆行驶过程中的状态量，其取值范围都是能够根据车辆的行驶极限进行预先估算的，因此基于各变量的合理取值上下限对其进行归一化处理。Actor 网络的输入为可通过常规车载传感器观测的行驶状态量，Critic 网络的输入包含两部分，第一部分是观测的行驶状态量，第二部分是Actor 网络输出的动作量，也即其对侧向车速的估计值。

全连接层：神经网络的主体部分是全连接层（包含激活函数层），在Actor 网络的设计中共采用了4 个全连接层，每个全连接层内含有48 个节点。在Critic 网络的设计中，状态量和动作量的路径中各采用了2 个全连接层，在通过加法层的整合运算后，又加入了2 个全连接层，每个全连接层也都含有48 个节点。

循环神经网络层：循环神经网络（recurrent neural network, RNN）是以序列数据为输入，在序列的演进方向进行递归的神经网络。RNN 的记忆性使其在对序列的非线性特征进行学习时能获得较好的效果，因此适用于本研究中采用非线性状态方程进行描述的车辆动力学特性。基于RNN 的上述优势，在Actor 网络和Critic 网络中分别加入一个循环神经网络层，每个层中含有100 个节点。

缩放层：在Actor 网络的最后需要加入一个缩放层，根据侧向车速的实际可能取值范围对神经网络的输出值进行缩放，其主要参数包括缩放层的增益和偏置。

2.4 奖励函数设计

奖励函数的作用是对智能体输出动作的作用效果进行评估，计算出奖励值反馈至智能体，指导其内部的策略更新和各个深度神经网络的参数调节。奖励函数的设计对智能体的训练效果影响很大，结合不同应用需求的具体情况，对奖励函数进行合理的选取设置，是充分发挥深度强化学习优势和提升学习效果的关键。在本研究所针对的应用中，奖励函数的目的是评估智能体对侧向车速估计的准确度，所设计的奖励函数为

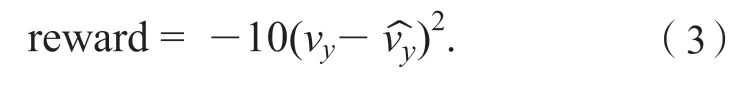
其中：vˆy是智能体对侧向车速的估计值，vy是训练过程中获取的侧向车速的真实值。vy可以来自于车辆动力学仿真模型，也可以来自试验样车上的专业测试仪器。

2.5 算法训练流程

在完成上述架构搭建、算法选取、神经网络设计、奖励函数设计之后，即可按照所选取的算法流程进行训练，本文DDPG 算法的核心训练流程如下。

首先，采用一组随机参数Φ对Critic 网络Q进行初始化，并用同样的参数Φt=Φ对Target Critic 网络Qt进行初始化；其次，采用一组随机参数θ对Actor网络π进行初始化，并用同样的参数θt=θ对Target Actor 网络πt进行初始化；

开始训练，在每一个训练时间步长中重复如下步骤1—8，直至训练结束：

步骤1：对于当前的观测S，利用Actor 网络π计算出对vy的估计值vˆy=π(S)+N，其中N是噪声模型生成的随机噪声；

步骤2：输出估计值vˆy，观察计算的奖励值R和下一个观测值S’;

步骤3：将经验(S,vˆy,R,S’)存入经验池Buffer;

步骤4：从经验池Buffer 中随机选取出M个经验(Si,vˆyi,Ri,Si’),i= 1, 2, …,M;

步骤5：对选取出的每个经验(Si,vˆyi,Ri,Si’)，计算其价值函数yi=Ri+γ Qt(Si’,πt(Si’|θt)|Φt);

步骤6：通过最小化来更新Critic 网络Q的参数；

步骤7：通过采用策略梯度（policy gradient）算法，来更新Actor 网络π的参数；

步骤8：采用平滑更新算法，来分别更新Target Critic 网络Qt的参数Φt和Target Actor 网络πt的参数θt。

3 仿真验证与对比分析

3.1 仿真与训练

为了验证本研究所提出的上述方法的有效性，在Matlab/Simulink 软件中搭建了仿真环境和深度强化学习算法。车辆模型基于Matlab/Simulink 中Vehicle Dynamics Blockset 工具箱所提供的Muscle Car 模型进行搭建，车辆在无限大的水平地面上进行多个片段的反复训练。车辆模型和仿真场景如图6 所示，车辆的主要参数如表1 所示。

图6 用于训练的车辆模型和仿真场景

表1 车辆模型的主要参数

在训练学习阶段中，每个训练片段持续10 s，车辆从静止开始加速，采用不同的驾驶员方向盘转角δ和车轮输出转矩的组合作为车辆模型的输入，对智能体进行训练。δ的输入包括150°的δ恒定值输入、斜率为30 (°)/s 且最大值为150°的δ斜坡输入、以及不同幅值和频率的δ正弦波输入，δ正弦波输入信号的幅值和频率特征如表2 所示，从δ到前轮转角的传动比为20。4 个车轮的输出转矩Ti分别在{50, 100, 150, 200 } Nm这4 个值中进行选取并随机组合。在本研究的训练中，受限于训练样本变量维度和仿真算力的约束，将不考虑整车质量的变化，而将其视为一个定值。

表2 训练过程中的方向盘转角输入信号

训练过程中的主要参数设置如表3 所示。

表3 训练过程的主要参数

训练的结束条件设置为：最近100 次训练片段得到的累计奖励平均值不小于阈值-100，即认为此时对侧向车速估计的准确度达到了要求。该阈值的选取基于式（3）中对奖励值的计算公式：将能够容忍的最大估计误差值所对应的奖励值，乘以单个训练片段中设置的最大步长数，即作为用于判断训练过程是否结束的累计奖励平均值的阈值。

某个训练过程的奖励值(reward)随训练片段次数(N)变化关系如图7 所示。在经过630 次训练之后，累计奖励平均值达到了设置阈值，此时认为训练过程完成。

图7 仿真训练过程中奖励值的变化趋势

3.2 效果对比与分析

完成训练之后，智能体中的Actor 网络（或称之为估计策略网络）即可用于对侧向车速进行实时估计。采用不在训练场景数据库中的全新的仿真场景验证其对侧向车速的估计效果，选用的是Vehicle Dynamics Blockset 工具箱中的双车道变换场景，如图8 所示。

图8 用于验证估计效果的双车道变换仿真场景

车辆以40 km/h 的初速度向前加速，当车速达到60 km/h 时开始进行双车道变换操作。

采用扩展Kalman 滤波（extended Kalman filtering，EKF）算法作为对照组。EKF 是在车辆状态观测中广泛应用的估计方法，可处理车辆模型中的轮胎非线性等因素。

在双车道变换场景中的侧向车速（vy）估计结果对比如图9 所示。

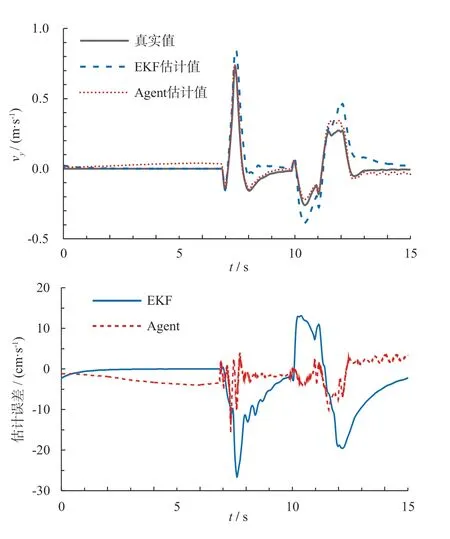
图9 双车道变换下的侧向车速估计效果验证

由图9 可知：智能体(Agent)在经过训练之后，其估计策略网络能够对车辆行驶过程中的侧向车速进行较为准确的估计。在车辆加速行驶和双车道变换的大部分过程中，估计值和真实值均较为接近，只在车道变换过程的后半部分存在一定的估计误差，且总体估计精度优于EKF 方法的估计值。

图9中2 种算法的估计误差的最大值和均方根（RMS）值如表4 所示。

由表4 可知：深度强化学习算法的最大估计误差比EKF 算法减小了40%，估计误差的RMS 比EKF 算法减小了58%。

表4 仿真工况中2 种算法的估计误差比较

3.3 算法应用的实时性探讨

如前所述，在完成了训练过程之后，只需将智能体中的Actor 网络部署到实车控制器中，即可实现对侧向车速的估计。因此，影响算法实时性的主要是Actor网络在控制器中的运算时长。以本文研究中设计的Actor 网络为例，其主要的运算量集中在4 个全连接层（每个全连接层包含48 个神经元节点）和1 个循环神经网络层（包含100 个节点）。

以全连接层的计算为例，一个全连接层中每个节点的输出值y=σ(wx+b)，其中：σ(·)是激活函数，x是上一层所有节点的输出值组成的向量（维度为48×1），w是权重系数向量，b是偏置值。因此完成单个节点的计算输出需要进行48 次浮点乘法运算和48 次浮点加法运算，以及1 次激活函数的运算；完成4 个全连接层中的所有节点的计算输出大约需要进行4×48×48 次乘法运算，4×48×48 次加法运算，以及4×48 次激活函数的运算。而循环神经网络层的计算量通常比普通的全连接层更大。

因此，对于传统的嵌入式控制器和单片机来说，进行深度神经网络的实时计算是存在难度的，需要具有并行运算能力的高算力平台（如GPU 和FPGA），才能较好地实现基于深度神经网络的估计算法的实时运行，这也是未来研究工作的方向之一。此外，从降低计算量的角度考虑，增加全连接层的层数比增加每个全连接层中的节点数更具性价比。

4 结 论

本文基于深度强化学习的范式，设计了四轮独立电驱动车辆的侧向车速估计方法。结合深度神经网络的非线性拟合能力和强化学习的训练模式，以易于测量的车辆行驶状态量为输入，通过对奖励函数、神经网络、训练场景的合理设计，实现了对车辆侧向车速的估计功能。

仿真结果表明：在经过充分的行驶场景训练之后，与扩展Kalman 滤波方法比较，本文智能体中的估计策略网络的估计误差降低了40%，误差的均方根降低了58%。因而，本方法提高了四轮独立电驱动车辆侧向车速的估计精度，不仅能够实现对车辆侧向车速的准确估计，还可以应用于对其他车辆动力学状态的实时估计。