狭缝节流气体静压轴承设计及其静态性能研究

于雪梅，徐宗泽，张飞，朱海鹏

（江苏海洋大学 机械工程学院，江苏 连云港 222005）

气体静压轴承因具有高速度、高精密、高寿命等显著优点，在超高速旋转机械、超精密加工机床、精密测量仪器、空间机器人等领域有着重要的应用[1-4]。气体静压轴承一般分为小孔节流、多孔质节流、狭缝节流等。如何提高气体静压轴承的静态特性成为许多学者研究的重点，其中，很多学者在轴承的表面开设单个或复合均压槽，这种方法可以大大提高气体静压轴承的静态特性[5]。于普良等[6-7]在狭缝节流气体静压轴承的基础上，设计了一种新型均压槽，该槽的径向和周向截面分别呈扇形和椭圆弧形，研究显示该槽可以大幅度提高轴承的静态性能。张亮等[8]采取狭缝节流、均压槽节流和均压腔节流的复式结构，建立了梯形均压槽，发现该均压槽的承载能力较普通均压槽提高很多。于贺春，王广洲等[9-10]利用有限差分法对人字槽进行数值计算，得出该槽型可有效提高狭缝节流气体静压轴承的动态性能。冯小磊等[11]比较了不同类型均压槽后，发现三角形均压槽对气浮轴承综合承载性能最佳。Tomohiko I等[12]提出并研究了一种轴向设置限位槽的气体静压轴颈轴承，并提高了该轴承的刚度。Yan Ruzhong等[13]基于CFD提出了直线形、扩展形等6种均压槽方案，研究表明采用均压槽可以使气体静压轴承保持均匀的应力并提高轴承的静态性能。

本文借鉴开设均压槽的方法，基于矩形均压槽，在狭缝节流气体静压轴承的表面开设周向呈矩形，且从节流孔到气膜方向呈现由浅至深结构的新型均压槽，并通过改变槽的深度、直径、数目和供气压力，阐释该均压槽对狭缝节流气体静压轴承静态性能的影响。

1 结构及原理

1.1 带均压槽结构

本文选取静态性能较为优越，且稳定性较好的狭缝节流气体静压轴承作为开槽对象[14-15]，在其表面开设周向呈矩形，且从节流孔到气膜方向呈现由深至浅结构的均压槽，结构如图1所示。ps为压力进口，当气体通过节流孔，流过槽结构时，产生节流效应，从而使轴承有一定的承载力，最后气体排出，此时压力为p0。

图1 带均压槽结构示意图

本文中各项计算参数如表1所示。

表1 计算参数

1.2 CFD模型

考虑计算量较大，本文先利用UG画好1/4的平面图，随后导入到 Gambit中采用Mesh/Quad/Pave/Apply命令，划分好网格后，在Geometry中将平面进行拉升，拉升过程中为方便操作，竖直方向上的数值扩大10倍，将对称边定义为周期边界，随后保存为mesh文件导入到Fluent。在Scale命令中将模型缩小10倍，打开能量方程，选择理想气体，定义进出口压力，进行计算。CFD模型如图2所示。

图2 气体流场示意图

2 数值计算

2.1 槽型区域的流场计算

当气体流经狭缝节流器时，热交换非常小，并且节流器的宽度是微米级。根据节流器的这两种特性，可将气体的流动简化为气体在2个平板中的一维流动[16]。假设气体沿x方向以速度u流动，气体在平板间的流动模型如图3所示。

图3 槽型区域计算示意图

当气体流场为一维稳定流场时，Naiver-Stokes方程和状态方程可分别简化为[17]：

式中：x为在x方向上的距离，mm；μ为平板间整体流速，m/s；ρ为供气的气体密度，kg/m3；dρ为大气密度，kg/m3。

由式（1）和式（2）得：

式中：η为气体粘性系数，Pa·s；y为在y方向上的距离，mm。

两平板间的质量流量为：

式中：m为两平板间的质量流量，kg/s。

由式（2）和式（3）得：

将式（5）转化得：

2.2 气膜间隙的流场计算

根据文献[18-19]可得：

式中：M为气膜中每等份的质量流量，kg/s；z为在z方向上的距离，mm。

根据边界条件积分计算可得：

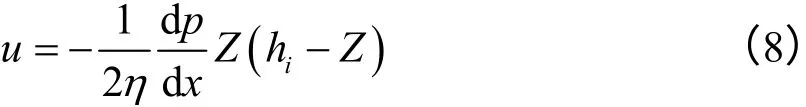
式中：ih为槽型平均厚度，μm。

结合式（2）和式（8）可得：

式中：b为常数；l为均压槽长度，mm。

综上可得：

2.3 有限差分法求解承载能力和刚度

假设所要求解的润滑介质为可压缩流体，即令ρ为常数，对式（10）进行积分，可得：

式中：W为承载能力，N。

承载能力在气膜厚度下的积分即为轴承刚度：

式中：K为轴承刚度，K/（N·μm-1）。

3 仿真结果及分析

3.1 有无均压槽结构比较

在参数条件相同的条件下，无均压槽结构和有均压槽结构的压力云图分布如图4所示，可以清晰的看出，带有由深至浅均压槽的气浮轴承的压力分布较无均压槽的轴承效果更好。由此，该均压槽可以提高狭缝节流气体静压轴承的承载能力。

图4 有无均压槽压力云图

3.2 不同槽结构深度的影响规律

保持其他各项参数不变，设定：De＝30 mm，Ne＝4，ps＝0.5 MPa，通过改变槽结构的深度（0.02、0.04、0.06、0.08 mm），来研究槽结构在该工况下对轴承承载能力和刚度的变化情况，结果如图5和图6所示。

由图5和图6可知，槽结构相同的深度下，随着气膜厚度的增加，承载能力呈缓慢减小趋势；在深度为0.02 mm时，刚度在一直减小，而深度在0.04 mm、0.06 mm和0.08 mm时，刚度曲线先增大到峰值，然后缓慢减小。气膜厚度相同时，槽结构深度越大，承载能力也越大，刚度则越小。可见，槽结构深度对气浮轴承的承载能力和刚度影响显著。

图5 承载能力变化曲线

图6 刚度变化曲线

3.3 不同槽结构直径的影响规律

保持其他参数不变，设定：he＝0.01 mm，Ne＝4，ps＝0.5 MPa，通过改变槽结构的直径（10、20、30、40 mm），来研究槽结构在该工况下对轴承承载能力和刚度的变化情况，结果如图7和图8所示。

由图7和图8可知，在槽结构直径为40 mm时，承载能力先是陡然减小，随后趋于稳定，在直径为10 mm、20 mm、30 mm时，承载能力一直在缓慢减小，刚度则呈现先增加后减少的趋势。相同气膜厚度的情况下，槽结构的直径越大，承载能力越大，刚度也越大，且当槽结构直径为40 mm时，刚度远大于其他直径的刚度，此时对应的气膜厚度为10 μm。

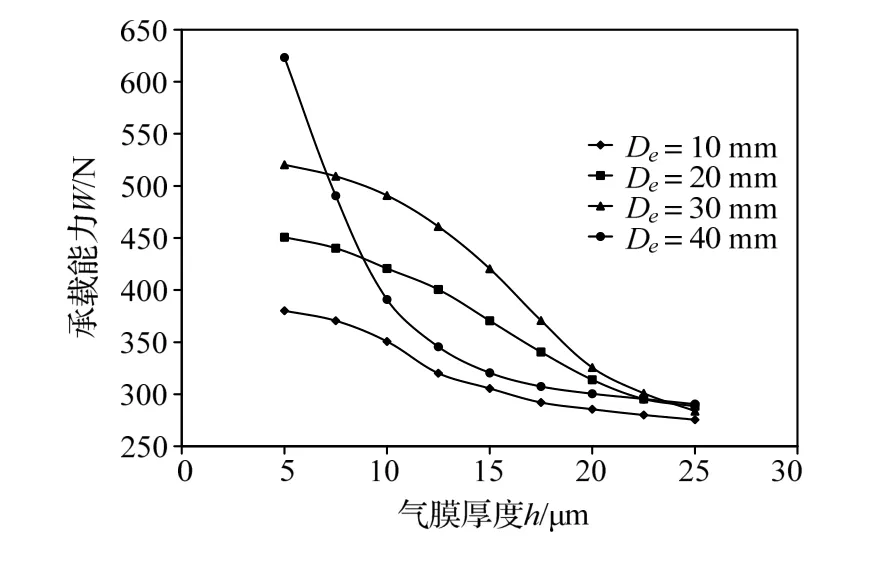
图7 承载能力变化曲线

图8 刚度变化曲线

3.4 不同供气压力下的影响规律

保持其他各项参数不变，设定：De＝30 mm，he＝0.01 mm，Ne＝4，通过改变供气压力（0.3、0.4、0.5、0.6 MPa），来研究槽结构在该工况下对轴承承载能力和刚度的变化情况，结果如图9和图10所示。

由图9和图10可知，供气压力相同时，轴承的承载能力随着气膜厚度的增大而减小，刚度则先增大后减小。气膜厚度相同时，供气压力越大，承载能力和刚度也越大，并且供气压力对最佳刚度对应的气膜厚度影响较小。

图9 承载能力变化曲线

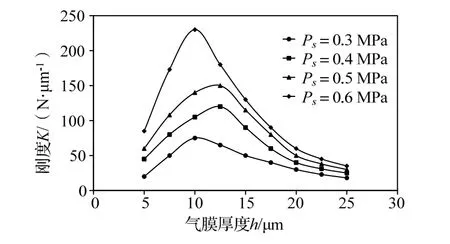
图10 刚度变化曲线

3.5 不同槽结构数目的影响规律

保持其他参数不变，设定：he＝0.01 mm，De＝30 mm，ps＝0.5 MPa，通过改变槽的数目（4、8、12、16个），来研究槽结构在该工况下对轴承承载能力和刚度的变化情况，结果如图11和图12所示。

由图11和图12可知，槽结构相同的数目下，承载能力随着气膜厚度的增大而减小，刚度则呈现先增大后缓慢减小的趋势。在气膜厚度相同的条件下，合理增加槽结构的数目则能够提升承载能力，且刚度也越大。由图可知最佳刚度在10～15 μm范围内，且增加槽结构的数目可以使最佳刚度提高。

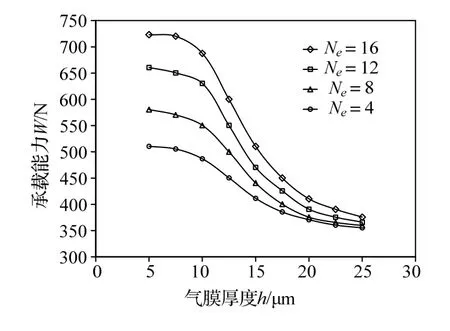
图11 承载能力变化曲线

图12 刚度变化曲线

4 结论

本文基于狭缝节流气体静压轴承的研究，在端面开设一个周向呈矩形且由深至浅的均压槽，研究该槽在不同的深度、直径、供气压力和数目的变化下，对轴承的承载能力和刚度的影响，得出以下结论：

（1）相较于无均压槽气浮轴承，采用有均压槽的狭缝节流气体静压轴承可以提高承载能力和刚度。

（2）气浮轴承在其他参数一定的条件下，随着槽结构深度、直径、数目和供气压力的增加，狭缝节流气体静压轴承的承载能力也增大且变化趋势都是缓慢升高。

（3）气浮轴承在其他参数一定的条件下，随着槽结构深度、直径、数目和供气压力的增加，刚度先增大后减小，刚度的变化趋势呈现先陡然上升，达到最大值后缓慢下降。

（4）本文中的槽型最大承载力对应的气膜厚度在5～10 μm之间。在10～15 μm之间，狭缝节流气体静压轴承有着最佳刚度。综上，轴承的静态性能最佳值对应的气膜厚度为10 μm。