铁道车辆扁疤识别与定量估计

李大柱，吴兴文，池茂儒，梁树林，许文天

（1.西南交通大学 牵引动力国家重点实验室，四川 成都 610031；2.西南交通大学 机械工程学院，四川 成都 610031）

列车在运行过程中由于紧急制动、车轮空转打滑或者钢轨表面有杂物时，车轮由滚动变为滑动，此时剧烈的摩擦形成的高温导致车轮踏面剥离、裂损、掉块等现象统称为平轮或车轮扁疤。扁疤是一种常见的轨道车辆车轮踏面损伤形态，会引起轮轨间产生周期性的振动冲击[1]。车轮扁疤不仅会增大列车的振动和噪声使乘坐舒适性下降，而且会加速车辆及轨道零部件的损伤，严重时会引发事故。因此开展车轮踏面扁疤故障实时诊断研究具有重要的理论意义和工程应用价值。

我国现有的车轮扁疤检测技术主要有超声波检测法、声音检测法、图像检测法和振动加速度检测法等。超声波检测技术是利用电磁超声波回波来定位车轮及车轮踏面缺陷的判断，检测效果较好，但此方法结构复杂技术难度较大，且不能对车轮扁疤进行定量检测[2]。声音检测法是根据声音信号大致判断车轮的扁疤，此方法安装简单，只能检测出扁疤所在车轮，并不能精确地判断扁疤的大小[3]。图像法是利用安装在轨道上的高速摄像头获取车轮踏面的图像，再通过图像处理技术来识别车轮状态，识别率较高，但该方法的缺点是成本高、安装困难[4]。振动加速度检测法又包括车辆振动加速度检测法和钢轨振动加速度检测法。钢轨振动加速度检测法是通过检测分析由列车引起的轨道振动加速度来检测车轮扁疤，只能定性地区分正常车轮和扁疤车轮，不能定量地判断扁疤长度[5]。车辆振动加速度检测法是利用安装在车辆上的加速度传感器来对车轮的运行状态监测，该方法的优势是安装简单、成本低且能对列车全程实时监测。

1 车轮扁疤故障诊断技术

1.1 奇异值差分谱降噪

奇异值差分谱降噪（Singular Value Decomposition，SVD）是一种有效的降噪技术，该方法的原理是将噪声对应的奇异值置零，保留信号对应的奇异值，从而将噪声从原始信号中剔除提高信噪比，该算法具有良好的稳定性在齿轮、轴承等的故障诊断中得到了广泛应用[6]。

式中：Hmn×为m×n阶的Hankel矩阵；N＝m＋n－1；Dm×n为无噪声干扰的信号子空间；Wm×n为噪声信号子空间。

对Hm×n进行奇异值分解，可得：

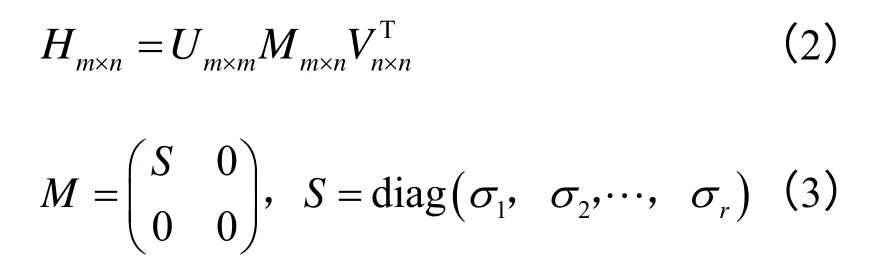
式中：Um×m、均为正交矩阵；Mm×n为非负对角阵；r为矩阵Hm×n的秩。

在矩阵Hmn×中从第二行起每一行数据比前一行数据滞后一个点，如果信号中包含有噪声相邻的两行数据之间就没有关联性。Hmn×中的数据中包含有噪声，对H矩阵进行奇异值分解得到的奇异值就不会有比较明显的突变。如果信号中不包含噪声，那么相邻两行之间的关联性比较强，此时Hmn×进行奇异值分解得到的奇异值就会有比较明显的突变[7]。由于信号的奇异值明显大于噪声的奇异值，因此利用奇异值差分谱中最大值的对应点k可以确定信号与噪声奇异值相分离的点。保留前k个有效奇异值而其他奇异值置零，再利用奇异值分解的逆过程得到重构矩阵XS，将XS依据相空间重构的方法进行逆变换，最终得到降噪后的信号[6]。

1.2 BP神经网络

BP神经网络（Back-propagation network）是由Rumelhart、McClelland于1985年提出的，是一种按误差逆传播算法训练的前馈网络，其具有优秀的自学习、自适应能力，是目前在故障诊断与状态监测中应用最多的多阶层前馈型神经网络模型[7]。BP神经网络由输入层、隐藏层和输出层组成，一般输入层和输出层为一层，隐藏层有一层或者多层，层与层之间依靠神经元与传递函数连接常见的三层神经网络拓扑图如图1所示。

图1 三层神经网络拓扑图

BP神经网络是通过大量的训练来建立输入层与输出层之间的映射关系，训练过程中不断地优化调整网络中的权值、阈值等参数，最终实现差平方和最小。整个训练学习的过程分为正向传播和反向传播两部分，首先在输入层输入向量经过隐含层处理在输出层输出向量，这是正向传播的过程，然后计算输出向量与实际向量之间的误差是否满足要求，如果不满足要求则按照原来的计算路径返回误差，这是反向传播的过程，优化调整各神经元的权值后重新逐层计算。反复执行正向传播和反向传播过程直到输出向量与实际向量之间的误差的平方和最小，训练学习过程结束[10]。

1.3 基于SVD和BP神经网络的车轮扁疤故障诊断方法

该方法主要有三个步骤，第一步是对采集到的轴箱振动加速度信号进行奇异值差分谱降噪处理后包络分析提取出信号中的低频分量。第二步是对比提取出的低频分量与计算得到的车轮扁疤引起轴箱振动加速度特征频率，诊断是否存在扁疤故障。第三步是对诊断中存在扁疤故障的信号计算出车轮扁疤引起轴箱振动加速度特征频率的1～4倍频对应的幅值作为特征向量输入到训练后的BP神经网络模型中对扁疤长度定量估计。该方法具体流程如图2所示。

图2 车轮扁疤故障诊断与定量估计流程图

2 扁疤故障仿真与信号特征提取

2.1 仿真模型建立

为研究在车轮扁疤故障状态下轴箱振动加速度的响应特征，本文基于多体动力学原理在SIMPACK中建立高速动车组动力学模型,首先基于有限元软件ANSYS建立柔性轮对和柔性轨道导入SIMPACK软件，然后在SIMPACK中建立轴箱、构架、车体等得到刚柔耦合模型并在轴箱上布置传感器，线路条件为施加了武广90谱的直线线路，仿真模型如图3所示。

图3 动车组车辆刚柔耦合模型

2.2 车轮扁疤故障仿真

因轴箱振动加速度响应特性不仅与列车运行速度相关，而且随着车轮扁疤长度的增长而增大[11]。仿真车速50～400 km/h的15个速度等级与扁疤长度20～90 mm的8种长度等级组合的120种工况，不同工况下采集到轴箱振动加速度峰值如图4所示。由图4可知同一扁疤长度下轴箱振动加速度峰值随车速的增大先增大后减小，同一速度等级下轴箱振动加速度峰值随扁疤长度的增大而增大。

图4 加速度峰值图

2.3 轴箱振动加速度信号特征提取

车轮扁疤故障的出现会引起车轮与轨道之间周期性冲击振动，导致列车轮在运行中出现周期性的垂向跳动[12]，此冲击的频率与轮对的转频率相关，计算公式为[13]：

式中：CF为车轮扁疤引起轴箱振动加速度特征频率，Hz；v为列车运行速度，km/h；R为车轮直径，m。

以车速v＝125 km/h、扁疤长度30 mm为例提取轴箱振动加速度信号特征。动力学模型中车轮直径R＝0.92 m、采样频率为10000 Hz、采样时间120 s，由式（4）可得，在此速度下CF＝12.014 Hz。在采集到轴箱垂向振动加速度信号中截取部分信号如图5所示，图5中虽可看出周期性成分，但无法直观地判断扁疤故障的存在。对截取的轴箱振动加速度信号进行FFT变换，得到轴箱振动加速度频谱图如图6所示。图6中由于轮对与轨道的共振轴箱在600 Hz、1300 Hz附近振动幅值较大。车轮扁疤引起的轴箱振动属于低频信号，由于高频振动的出现淹没了车轮扁疤引起的低频振动，因此在图6中无法直观地诊断出车轮扁疤的存在。

为了快速准确地从轴箱振动加速度中识别出车轮扁疤故障，本文提出使用奇异值差分谱法对采集到的轴箱振动加速度信号降噪处理，消除信号中随机噪声的干扰，并忽略信号中幅值较小的频率成分，提取出车轮扁疤故障所引起的幅值较大的主要频率成分。对图5中的原始信号利用奇异值差分谱法降噪后的信号如图7所示。降噪后的信号周期性更加直观，但其中仍存在大量的高频信号无法直接识别出车轮扁疤引起轴箱振动加速度特征频率。对降噪后的信号求包络，包络后的信号如图8所示。最后对包络后的信号进行FFT变换得到幅频图如图9所示。图9中可清晰直观地找到12.01 Hz、24.02 Hz、36.04 Hz、48.05 Hz等频率，分别与车轮扁疤引起轴箱振动加速度特征频率的1倍频、2倍频、3倍频、4倍频相对应，图9中去除了图6中的部分干扰频率成分，大幅度提高了信噪比，从图9中可快速准确地诊断出车轮扁疤故障的存在。

图5 车轮扁疤故障仿真信号

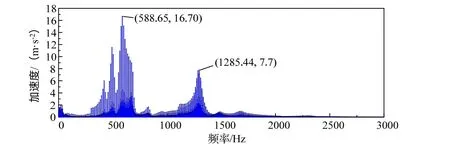
图6 车轮扁疤故障仿真信号频谱图

图7 降噪后的仿真信号

图8 降噪包络解调后的仿真信号

图9 降噪包络解调后的仿真信号频谱图

3 BP神经网络模型的建立与验证

本文结合机器学习的优势运用列车运行中轴箱振动加速度和车速来实现对车轮扁疤故障的定性识别同时对扁疤的长度进行定量估计。从图4可知，速度在125～400 km/h之间车轮扁疤长度、车速与轴箱振动加速度峰值之间一一对应，而在速度低于125 km/h的时车轮扁疤长度、车速与轴箱振动加速度之间并不满足一一对应。因此，仅通过轴箱振动加速度峰值和扁疤长度及车速建立神经网络模型，在车速低于125 km/h时无法精确的估计车轮扁疤长度，因此本文提出以车轮扁疤引起轴箱振动加速度特征频率的1～4倍频和车速作为特征向量来定量的估计扁疤。

3.1 神经网络模型的建立与训练

为了更加精确的定量估计车轮扁疤长度，本文提出一种在不同速度等级下利用车轮扁疤引起车轮扁疤引起轴箱振动加速度特征频率的1倍频、2倍频、3倍频、4倍频所对应幅值与车轮扁疤长度Lf和车速v之间的映射关系，将特征频率CF的1倍频、2倍频、3倍频、4倍频对应的幅值A1、A2、A3、A4作为特征向量用于神经网络的训练学习。然后再用训练后的模型对出现扁疤故障的车轮进行定量的估计来实现对车轮踏面的实时监测。

构建数据集，将车速从50～400 km/h平均分为15个速度等级，扁疤长度从20～90 mm平均分为8个长度等级，仿真组合速度等级与扁疤长度等级得到120种不同的工况，并采集各工况下的轴箱振动加速度信号，将加速度信号经SVD 降噪后求包络最后快速傅里叶变换，提取该车速下车轮扁疤引起轴箱振动加速度特征频率CF的1倍频、2倍频、3倍频、4倍频所对应的幅值A1、A2、A3、A4，将得到的120组数据作为训练集。为了加快BP神经网络的收敛速度，对训练集和测试集进行归一化处理，用S型激活函数将同一类数据归在[0,1]内，S型激活函数归一化公式为[8]：

式中：yi为归一化后的数据；xi为原始数据；xmax为原始数据中的最大值；xmin为原始数据中的最小值。

BP神经网络模型中需要设置隐含层数、训练次数、目标误差、学习效率等参数。训练次数设为1000次，学习效率选取为0.01，目标误差为0.00001，隐含层数计算公式为[8]：

式中：m、n、j分别为隐含层数、输入特征向量个数、输出向量个数；α为常数，取值范围在1～10之间，该模型的训练中隐含层数取9层。

将归一化后的训练集数据导入模型进行训练，经过不断地优化权值直到输出向量在目标误差之内模型训练结束。

3.2 神经网络模型的验证

为验证本文提出扁疤故障诊断方法的有效性，随机取表1中的10种工况作为测试集对神经网络模型的性能进行测试。将测试集数据归一化处理后导入到训练后的模型中，得到车轮扁疤长度估计值及估计值与真实值之间的方差

如表1所示。测试集数据扁疤长度估计值与真实值的对比如图10所示，扁疤长度估计误差如图11所示。通过验证可知运用本文提出的车轮扁疤诊断方法对车轮扁疤长度估计误差在3.5 mm内，可见利用车轮扁疤引起轴箱振动加速度特征频率倍频的幅值及车速作为特征向量训练的BP神经网络模型可以较准确地估计出车轮扁疤长度，有力地推动了车辆状态实时监测的发展。

表1 测试集数据

图10 扁疤长度估计值与真实值对比图

图11 测试样本误差

4 结论

本文提出了SVD和BP神经网络相结合的车轮扁疤故障诊断方法，并对该方法的有效性进行了验证。SVD可以有效的对信号进行自适应降噪，剔除信号中的噪声及幅值较小的分量提高信噪比，SVD的使用使车轮扁疤故障的识别更加的迅速、直观、准确。经验证，以车轮扁疤引起轴箱振动特征频率的1～4倍频对应的幅值和车速作为输入向量、以扁疤长度作为输出向量建立的BP神经网络模型对扁疤长度的估计误差在3.5 mm内，此方法可实现对列车车轮运行状态的实时监测，因此SVD与BP神经网络的结合对车轮扁疤故障的诊断具有重要的理论意义和工程应用价值。