探究一道以卡特兰数为背景的概率题

安徽省淮南第二中学(232001) 赵帅

一、原题呈现

(淮南第二中学届高三模拟)某中学为了丰富学生的课外生活,减轻学生的生活压力,组织学生开展以班级为单位的猜谜语比赛,规定每班的初始分为0 分,随机抽取题目,猜对得5 分,猜错扣5 分,并且猜测结果只有“对”与“错”两种,设高二年级某班学生猜对的概率为,猜错的概率为,记“该班学生完成n次猜谜语后的总分为Sn”.若规定积分扣到零分则被淘汰(第一次输也会被淘汰),求S5=5 的概率.

解析S5=5,即总共猜谜语5 次,猜错2 次,又由Si≥5(i=1,2,3,4),可得共有以下可能:

①第一次和第二次猜对,第三次猜错,第四次猜对,第五次猜错;

②第一次、第二次和第三次猜对,其余两次猜错.故所求概率为:

二、问题一般化与变式

易知,若猜谜语的次数为奇数,则猜正确和猜错误的次数中二者必为一奇数一偶数,则最后的得分必为5 的奇数倍;若猜谜语的次数为偶数,则猜正确和猜错误的次数中二者必为两奇数或两偶数,则最后的得分必为5 的偶数倍.

在满足规定:积分扣到零分则被淘汰(第一次猜错也会被淘汰)的情况下,则S2n+1=5×(1+2m)=10m+5(m,n∈N)与S2n=5×2m=10m(m,n∈N∗)概率为多少?

分析要解决这个问题,先从解决S5=5 的概率入手.我们可建立一个坐标“棋盘”,为了简洁,纵坐标为得分的.如图1.

图1

首先,初始情况对应图中O点,由于第一次猜谜语一定要赢,则必须到达A(1,1)点,然后沿着最短路径到达B(5,1)点(过程中必有两次正确两次错误).显然符合规定的路径条数有且只有两条,故所求概率为:

显然这种解法易于观察,但对于研究更一般的情形很难解决.所以对解法做出以下调整.

若不考虑规定,则从A点到B的最短路径数为=6,但很显然6 条最短路径中并不是每个都符合规定(即路径要在x轴上方),为此,取B′(5,−1),则可发现,不满足规定的A点到B点所有经过x轴的最短路径与A点到B′点所有最短路径为一一对应的关系,则它们的路径数相同,故不符合规定的最短路径数为=4.故所求概率为

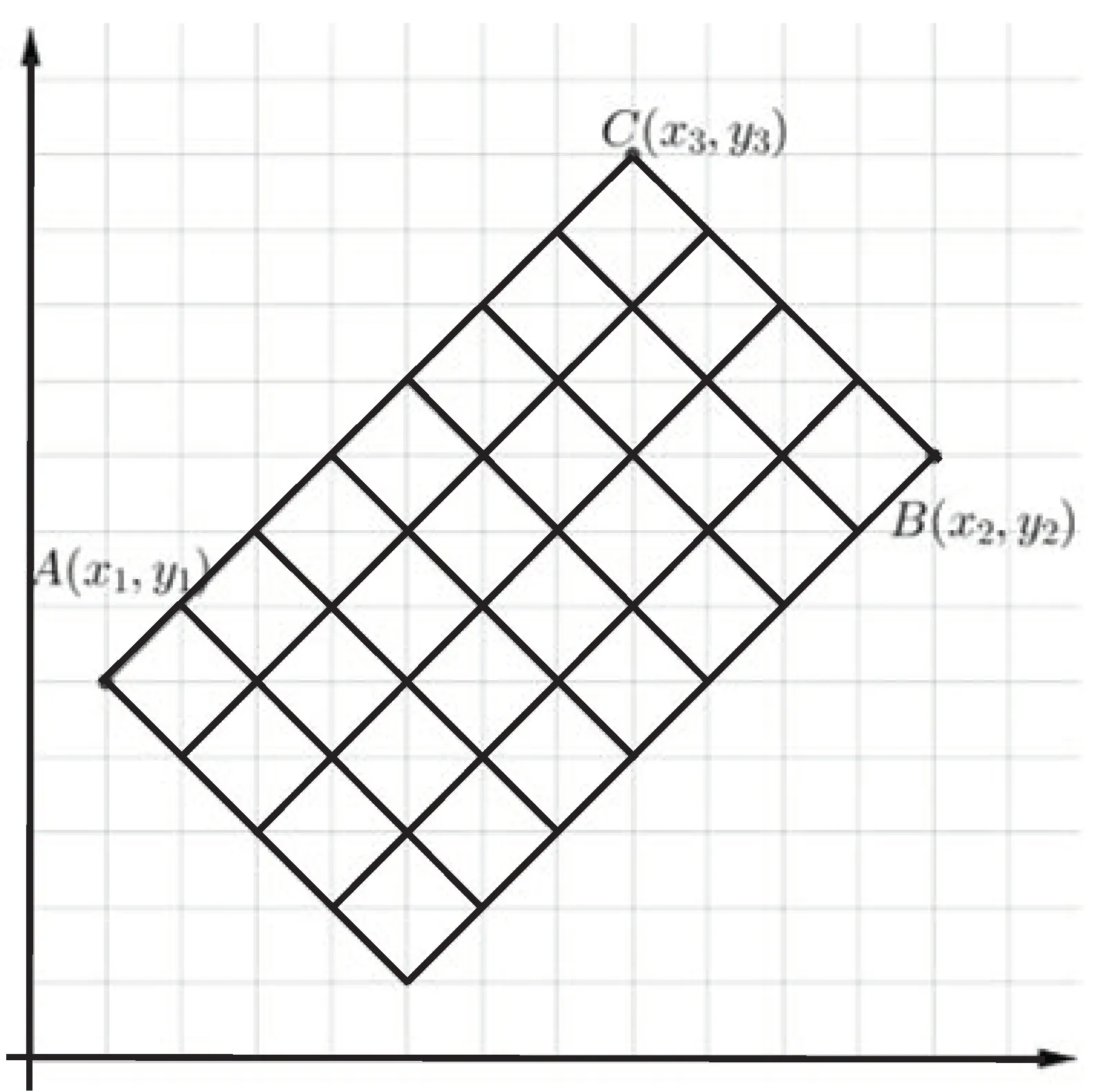
图2

据此,我们根据以上分析可得以下定理,并证明之.

定理1 由整点A(x1,y1)到整点B(x2,y2)的所有最短路径条数为

证明可知直线AC的方程为:y−y1=x−x1,直线BC的方程为:y−y2=−(x−x2),解得C点坐标为,故由点A到点C需要经过x3−x1=次步骤,同时也为共x2−x1步骤中所有“上升”的步骤数.由组合知识可得,由整点A(x1,y1)到整点B(x2,y2)的所有最短路径条数为

定理2 由整点A(x1,y1)到整点B(x2,y2)(其中y1>0,y2>0,x2−x1≥y1+y2)图象恒在x轴上方(不含x轴)的所有最短路径条数为

证明由定理1 可知,为整点A(x1,y1)到整点B′(x2,−y2)(点B关于x轴的对称点)的所有最短路径数.即证由整点A(x1,y1)到整点B(x2,y2)图象经过x轴所有最短路径数等于由整点A(x1,y1)到整点B′(x2,−y2)的所有最短路径数.设P为由点A到点B所有经过x轴的最短路径构成的集合,P′为由点A到点B′所有最短路径构成的集合,即证|P|=|P′|.下证P与P′为一一映射.

设由点A到点B的最短路径中与x轴的第一个交点为点M,则由点M到点B的路径与由点M到点B′的路径均关于x轴对称,且剩余路径均相同,显然P与P′为一一映射,故|P|=|P′|,定理成立.

变式1 若积分扣到零分则被淘汰(第一次猜错也会被淘汰),求S9=15 的概率.

解设猜对的次数为x,猜错的次数为y,则有x+y=9且x−y=3 解得x=6,y=3.由于规定,则需求出从(1,1)点到(9,3)点的最短路径条数与(1,1)点到(9,−3)点的最短路径条数之差,则可通过构造棋盘得:

变式2 若积分扣到零分则被淘汰(第一次猜错也会被淘汰),求S2n+1=10m+5(m,n∈N)与S2n=10m(m,n∈N∗)的概率.

解对于S2n+1=10m+5(m,n∈N),设猜对的次数为x,猜错的次数为y,则有x+y=2n+1 且x−y=2m+1 解得x=m+n+1,y=n−m.由于规定,则需求出从(1,1)点到(2n+1,2m+1)点的最短路径条数与(1,1)点到(2n+1,−2m−1)点的最短路径条数之差,则可通过构造棋盘得:同理,对于S2n=10m(m,n∈N∗),可得:

三、链接高考并推广

题目(2016年高考全国Ⅲ卷)定义“规范01 数列”{an}如下:{an}共有2m项,其中m项为0,m项为1,且对任意的k≤2m,a1,a2,···,ak中0 的个数不少于1 的个数.若m=4,则不同的“规范01 数列”共有( )

A.18个 B.16个 C.14个 D.12个

解记每项取1 得1 分,取0 扣一分.则此“规范01数列”的个数为:由(1,1)点到(8,0)点且图象恒在直线y=−1 图象上方的最短路径条数,构造棋盘,也即:由(1,2)点到(8,1)点且图象恒在x轴上方的最短路径条数,即:

推广定义“规范01 数列”{am+n} 如下:{am+n}共有m+n项,其中m项为1,n项为0,且对任意的k≤m+n(m≥n),a1,a2,···,ak中0 的个数不少于1的个数,求不同的“规范01 数列”个数.

解记每项取1 得1 分,取0 扣一分.则此“规范01 数列”的个数为:由(1,1)点到(m+n,m−n)点且图象恒在直线y=−1 图象上方的最短路径条数,也即:由(1,2)点到(m+n,m−n+1)点且图象恒在x轴上方的最短路径条数,即:

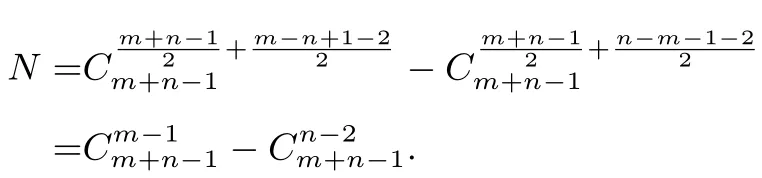
综上,再进行深入研究可知问题的结论背景直指组合数学中的“卡特兰数”(组合数学中一个常出现在各种计数问题中的数列,其在出栈次序问题,凸多边形三角划分问题,信息学中有很多得应用).我们可通过构造棋盘模型,将原本复杂的问题变为更为具体清晰,为解决这类概率(计数)问题提供了便利.