一个高中数学建模问题的探究与思考*

佛山市南海区第一中学(528200) 徐守军

《普通高中数学课程标准(2017年版2020年修订)》将数学建模作为高中数学课程的一个组成部分,明确将数学建模列为六大数学学科核心素养之一,并指出:数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养.数学建模是高中生数学学习的一种新尝试,为学生提供了自主学习的空间,有助于学生体验数学与日常生活的联系,有助于学会运用数学知识解决生活中的问题,更有助于体会数学在生活和其他学科中的价值.

1 数学建模的内涵

在高中阶段,很多学生仅仅把数学当成是为了升学学科,对其在现实世界中的应用不甚了解,其中很多人高考之后便不再关注数学.这对学生未来发展不利.为了破除这样的观念,教师需要在高中教学乃至整个基础教育阶段中常常渗透数学建模思想,让学生从心里认同数学在现实世界的作用.

数学建模过程主要包括以下4个步骤:①在实际情境中从数学的视角发现问题(章建跃对这一步骤表述为“对现实问题进行数学抽象”); ②提出问题、分析问题、建立模型;③确定参数、计算求解; ④检验结果、改进模型,最终解决实际问题.学生在实际问题的解决过程中怎么建模是关键,下面以一个“停车距离问题”为例来研究数学建模过程.

2 数学建模的过程

2.1 问题的提出

道路安全关系到千家万户,随着经济的发展,家用小汽车越来越普及,然而车辆在行驶过程中经常会遇到一些突发状况,如果驾驶员及时采取紧急制动,需要多远才能停下来呢?另外,在我国道路交通安全条例第80 条中明确规定,高速公路上,车速超过100 公里每小时,应与同车道前车保持100 米以上的车距.规定100 米以上车距的依据是什么呢?

2.2 问题的分析

汽车安全距离一般要大于停车距离,影响停车距离的因素通常包括许多方面,如驾驶员反应时间、汽车行驶速度、天气状况、道路情况、汽车轮胎纹路、刹车效果等.总结起来,大致分为两大类:反应时间(反应距离)、刹车效果(制动距离).汽车紧急制动大概要经历以下过程,首先是发现危险,做出刹车决定,并踩下刹车.其次是驾驶员踩下刹车,直至汽车完全停止.我们将汽车在反应时间行驶的距离称为“反应距离”,在制动过程中滑行的距离称为“制动距离”.

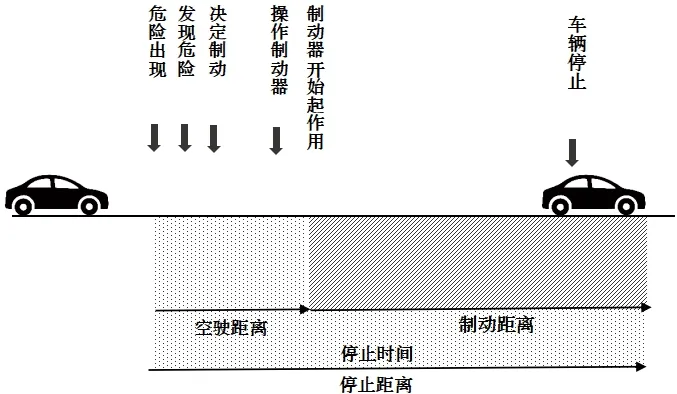
图1

2.3 模型的建立

由以上分析可知,停车距离包括反应距离和制动距离,设停车距离为d,反应距离为d1,制动距离为d2,得到停车距离为d=d1+d2.

(1)假设反应时间内车辆匀速行驶,速度为v,驾驶员反应时间为t,根据物理知识得到反应距离d1=atv,其中a为(大于0)待定系数.由于t很难确定具体的数值,因此,最终只能确定d1与v成正比,把这个关系表示为d1=av.

(2)假设刹车受力大小近似等于汽车轮胎与路面的摩擦力,制动距离是刹车受力与汽车速度的函数.根据物理知识,例如能量守恒、牛顿第二定律,得d2=,其中a1为加速度,得到制动距离与汽车速度平方成正比,不妨表示为d2=bv2,其中b为待定系数,b=.

综上,可以建立数学模型d=d1+d2=av+bv2.

2.4 模型的求解

通过问题的分析、模型的建立,把实际问题转化为数学问题,首先思考:

(1)是不是行驶速度越快,停车距离越大?

(2)是不是反应时间越长,停车距离越大?

接下来,就是运用数学模型来解决问题.模型的系数是由模型的假设和获取数据的方法确定的,一个好的模型,当采集的数据发生变化时,模型系数也会跟着变化.收集数据方法很多,可通过实验获得数据,也可根据网络获取数据.注根据表中所给数据,可计算相应参数(a,b)取值.

结合以上数据,通过不同计算方式,都可近似求解模型.

解法一由表1 计算的每一行中相应a和b的值,我们发现a和b的波动都不是很大,它们的平均值分别为a ≈0.209,b ≈0.0058,这组数据可以作为对参数a和b的一种估计.于是,通过试验数据得到了停车距离模型一:d=0.209v+0.0058v2.

表1 美国公路局公布的试验数据(来源网络)

解法二由于在d1=av中d1与v线性相关,由线性回归分析知数组满足d1=av.由表1 中的试验数据计算得=16.8231,=80.3846,因此a=≈0.209.同理,d2与v2线性相关,可求得b=≈0.0062.通过试验数据得到了停车距离模型二:d=0.209v+0.0062v2.

2.5 模型的评价

对两种模型进行比较,根据表1 数据,不妨设两种模型分别d3=0.209v+0.0058v2,d4=0.209v+0.0062v2,则经过误差计算得表2:

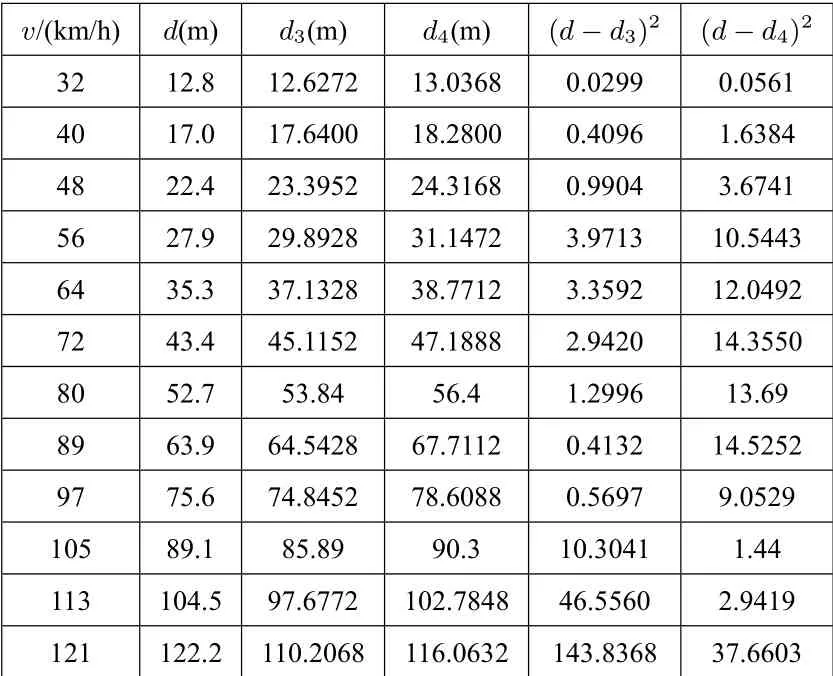
表2 模拟误差计算

对表2,我们分别求最后两列值之和得:

D1=0.299+···+143.8368=214.6818,

D2=0.0561+···+37.6603=121.6274.

显然,D2< D1,所以模型二d=0.209v+0.0062v2误差和更小,模型效果更好.

说明(1)模型中参数的确定方法有时是不唯一的,科学地选择参数可以有效地减小模型的误差; (2)在建立模型过程中,“基本假设”没有考虑影响停车距离的非关键因素,但在实际生活中,由于各种客观因素影响,有时非关键因素也会成为关键因素.

2.6 模型的应用

回应课前问题,法规中“100 米以上”的依据是什么?我们发现,当速度达到100 公里每小时时,根据模型计算,停车距离达到82.9m,实际操作过程中,可能存在一定误差,还可能存在驾驶员违规等现象.法规为了尽可能保证行驶安全,才规定了100 米以上的要求.

3 数学建模的步骤

从现实世界中发现问题,提出问题、分析问题、收集数据、建模模型、求解模型、评价模型,最后又回到现实生活应用模型.如图2 所示.

图2

4 数学建模教学思考

研究停车距离问题的过程就是数学建模的过程,在建模过程中根据实际问题进行数据的收集与处理,从而建立相应的模型、优化模型并应用于实际问题.

4.1 数学建模带来课堂变革

本节课相比较传统的“老师讲学生听”的教学模式,数学建模中的合作探究环节使学生更多的参与到课堂中来,课前需做好相应的小组分工,在课堂上有明确的小组合作任务,并给予充分的时间进行小组合作探究,充分的思考和讨论提出的问题,提升学生自主学习、自主归纳的能力.

4.2 数学建模要重视数据处理

本节课借助物理背景确定数学模型,教学重点从数学模型的探究,调整到数据处理与数学模型的优化上来,将重点落在系数的求解与模型的优化,这样的设计更贴合学生学情,让学生充分进行探究,分享各种方法在实现数学建模过程中的优与劣,符合学生的最近发展区.同时,培养了数学核心素养,从而提升学生的综合能力.