透过观察 抓住本质
——巧解排列组合中的有序数组问题
鲁和平
(浙江省嘉善第二高级中学,314100)
在高中数学排列组合问题教学中,学生有时会遇到一类有序数组问题.这类题目都有一个华丽的外表迷惑学生,需要我们用一双慧眼由表及里、去伪存真,透过现象看本质,只有通过不断转化命题方能抓住问题最本质的内核,使问题冰消获解.
一、抽丝剥茧,始见真容
有些题目,单从外表来看,学生就已望洋兴叹.但如果我们冷静分析,将所有已知条件进行转化与化归,就会有“蓦然回首,那人却在灯火阑珊处”的感觉.
例1设∆ABC的内角满足A≤B≤C,且cos 20A=cos 20B=cos 20C=1,则满足要求的数组(A,B,C)共有______个.
解由条件可知20A=2k1π,20B=2k2π,20C=2k3π,其中k1,k2,k3∈N*,k1≤k2≤k3.在∆ABC中,由A+B+C=π,可得20(A+B+C)=2(k1+k2+k3)π=20π,即k1+k2+k3=10.
用枚举可知(k1,k2,k3)=(1,1,8),(1,2,7),(1,3,6),(1,4,5),(2,2,6),(2,3,5),(2,4,4),(3,3,4),相应的(A,B,C)共有8个.
二、删繁就简,水落石出
有些题目条件纷繁无序,求解时往往要借力于多次的命题转化,甚至要随时借助函数的神力,才能拨开云雾见天日.
例2若正整数a,b,c,d满足a+b=c+d,ac=bd,ad=bc,且20≤ab+bc+cd+da≤2 020,则满足以上条件的有序数组(a,b,c,d)共有多少个?
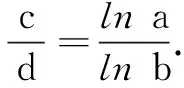
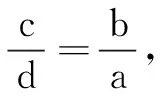
设f(x)=xlnx,则f(a)=f(b),又f(x)在(2,+∞)单调增,故a=b.又ac=bd,故c=d.再由a+b=c+d,可得a=b=c=d.结合20≤ab+bc+cd+da≤2 020,可得5≤a2≤505,故3≤a≤22,相应有序数组(a,b,c,d)共有20个.
若a=1或b=1,同理可得a=b=c=d=1,此时ab+bc+cd+da=4,与已知条件矛盾.
综上,所求有序数组(a,b,c,d)共有20个.
三、快速链接,脑洞大开
如果我们大脑里储存的数学知识容量大且结构佳,在审题时就能浮想联翩,快速链接,慧眼识真金.
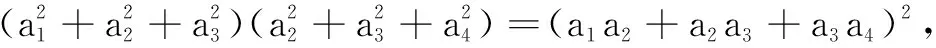
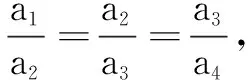
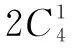
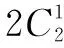
由加法原理,可知所求(a1,a2,a3,a4)共有38个.
四、条分缕析,思路井然
有些问题存在多种可能性,无法一言以蔽之.那就需要我们思维缜密,把各种可能性考虑周全,再按照一定标准进行分类讨论,则可使思路既有条理又流畅清晰.
例4已知∆ABC的三边长a,b,c(a≤b≤c)均为正整数,且满足(1)a,b,c成等比数列;(2)a,b,c中至少有一个等于100.求符合要求的三元数组(a,b,c)的个数.
解依题意,a+b>c,b2=ac.
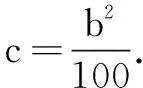
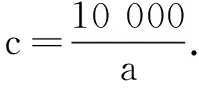
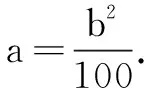
由于数组(a,b,c)=(100,100,100)一共出现了3次,综上得三元数组(a,b,c)共有7+4+2-2=11(个).
例5设正整数x,y,z满足1≤x,y,z≤6,且10整除xyz,则有序数组(x,y,z)共有多少个?
解因为1≤x,y,z≤6,若正整数x,y,z的乘积xyz能被10整除,则有以下3种情形:
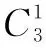
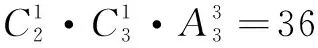

综上,所求有序数组(x,y,z)共有9+36+27=72(个).
五、筑巢引凤,模型转化
对于很抽象的问题,我们应该学会退步思考,一直退回到我们最熟悉、最原始的状态,然后借助于已有的思维模型,化险为夷,柳暗花明.
例6从数1,2,3,…,14中取出由小到大的三个数a1,a2,a3,满足a2-a1≥3,a3-a2≥3,则所有符合上述要求的有序数组(a,b,c)共有多少个?
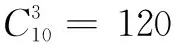
例7设a,b,c,d∈{-1,0,1},若有序数组(a,b,c,d)满足a+b,c+d,a+c,b+d互不相同,则称(a,b,c,d)为“好数组”,求满足题设的“好数组”(a,b,c,d)的个数.
解依题意,若a,b,c,d的取值为“2个1,1个0,1个-1”,或“2个-1,1个0,1个1”时,有序数组(a,b,c,d)才有可能成为“好数组”.
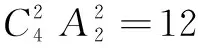
当(a,b,c,d)的取值为“2个-1,1个0,1个1”时,同理可得 “好数组”共有8个.
综上,“好数组”一共有16个.
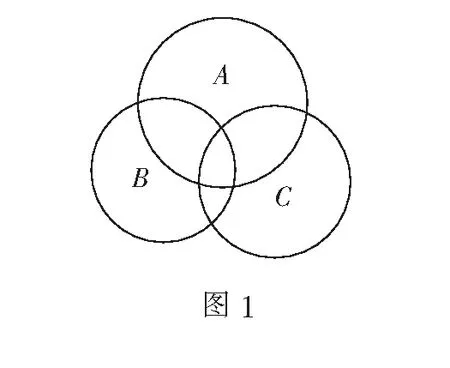
例8设集合A∪B∪C={1,2,3,…,9},则三元有序数组(A,B,C)共有______个.
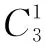
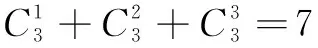
同理,其它8个数出现的可能性都有7种.
如图1,用3个圆圈分别表示集合A,B,C,则图中一共有7个独立的区域,每一个数都可以选择这7个区域的任何一个区域放置.故有序数组(A,B,C)一共有79个.
六、以点带面,退位思考
当一个问题非常抽象时,就应该毫不犹豫地退位思考.从最基本、最原始的情形入手,找出解决问题的规律,然后如法炮制,就能彻底解决抽象的问题.
例9若正整数a,b,c,d,e,f,g满足1≤a,b,c,d,e,f,g≤8,并且a+b+c+d+e+f+g-abcdefg=6,问满足要求的有序数组(a,b,c,d,e,f,g)共有多少个?
解先从最简单的情形入手分析.由于1+1+1+1+1+1+1-1·1·1·1·1·1·1=7-1=6,故此时有序数组(a,b,c,d,e,f,g)=(1,1,1,1,1,1,1),有1个.又1+1+1+1+1+1+x-1·1·1·1·1·1·x=(6+x)-x=6,x≠1,由于x有7种摆放位置,故对于给定的x,有序数组(a,b,c,d,e,f,g)共有7个.
又因为x可取2,3,4,5,6,7,8,故有序数组(a,b,c,d,e,f,g)共有1+7×7=50(个).
七、整体思考,剔除另类
在解决排列组合问题时,可以先从大处着手考虑问题,再将不合要求的情形排除(同时注意将过多排除的情形进行弥补).
例10题同例5.
解x,y,z的取法共有63种,x,y,z都不取2,4,6的取法共有33种,x,y,z都不取5的取法共有53种,因为{1,3,5}∩{1,2,3,4,6}={1,3},x,y,z都不取2,4,5,6的取法共有23种,故有序数组(x,y,z)共有63-33-53+23=72(个).

