含参不等式取值范围问题的常用求解策略
——以一道典型试题为例
解才先
(江苏省高邮中学,225600)
不等式是高中数学的一条主线,高考中对不等式的考查注重与函数相结合,需运用等价转化、分类讨论、数形结合等思想解决问题.其中含参不等式恒成立求参数取值范围问题因思维容量大、知识储备要求高,需要有较强的分析与运算能力,充满思考性与挑战性.本文结合一道典型试题,谈谈处理这类问题的一般策略与解题方向.
试题设函数f(x)=aex,x∈R.
(1) 当a=1时,过原点作y=f(x)的切线,求切线方程;
(2) 若不等式xf(x)-x+2>lnx对于x∈(0,+∞)恒成立,求实数a的取值范围.
分析本题第(1)问考查导数的几何意义,过程较简单,这里从略.第(2)问由不等式恒成立求参数的取值范围,解题的关键是将不等式的变形转化,主要是转化为求函数的最值,考查学生的逻辑思维能力、运算求解能力,属于难题.下面给出处理问题的常见策略.
策略1分离参数法
求参数取值范围,一般优先选用分离参数构造函数法,转化为求函数最值问题.需要注意得是该方法的参数要易于分离,并且构造的函数便于求最值.



当x∈(0,x1)时,m(x)>0,得g′(x)>0,有g(x)单调增;当x∈(x1,+∞)时,m(x)<0,得g′(x)<0,有g(x)单调减.所以gmax(x)=g(x1).
因为m(x1)=3-lnx1-x1=0,所以有lnx1=3-x1,两边取指数式,可得x1=e3-x1,即x1ex1=e3.

策略2同构法
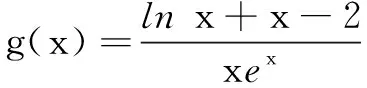

令t=xex,则lnt=ln(xex)=lnx+x,易得t∈(0,+∞),所以


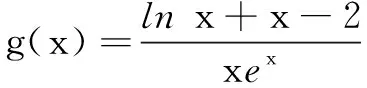

令t=lnx+x,则xex=eln xex=et,容易求得t∈R,且


策略3直接构造函数法
求参数的取值范围,若采用分离参数构造函数法,会遇到讨论麻烦,或进行参数分离容易,但构造的函数最值不易求出,这样参数分离法不可行,需采用直接构造函数法并结合题目条件求出函数最值来解决问题.这往往也许是出题人故意而为之的,下面的解法4可以充分体现这一点.
解法4由xf(x)-x+2>lnx对x∈(0,+∞)恒成立,整理得axex-x+2-lnx>0.
令g(x)=axex-x+2-lnx(x>0),则需gmin(x)>0.

(1)当a≤0时,g′(x)<0,g(x)在(0,+∞)单调减,且g(e)=aee+1-e+1<0,与g(x)>0在x∈(0,+∞)恒成立矛盾.
(2)当a>0时,令m(x)=axex-1,则m′(x)=a(x+1)ex>0,m(x)在(0,+∞)单调增,此时需要找应用零点定理的“支撑点”.


=0.
所以,当x∈(0,x0)时,m(x)<0,即g′(x)<0,g(x)单调减;当x∈(x0,+∞)时,m(x)>0,即g′(x)>0,g(x)单调增.则
gmin(x)=g(x0)
=ax0ex0-x0+2-lnx0
=3-(x0+lnx0).
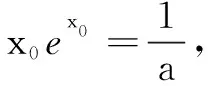

回顾求含参不等式恒成立范围问题,除了上述主流解题方法,有时还采用二次函数法、变换主元法等求解参数取值范围,需要我们不断归纳总结.心理学家罗杰斯指出:“在学习过程中获得的不仅是知识,更重要的是获得如何进行的方法或经验”.作为教师应该努力引导学生获取知识的同时,逐步形成善于观察、善于思考、善于总结的良好习惯.

