兼顾时序特性和不确定性的柔性配电网概率网损分摊方法

吴科成，吴晗，王凤学，曲毅，董红

(1. 广东电网有限责任公司，广州 510600；2. 华南理工大学，广州 510640; ；3.广东电网有限责任公司电网规划研究中心，广州 510030；4.广东电网广州供电局，广州 510610)

0 引言

网损的公平、合理分摊一直是供用电双方广泛关注的问题。而分布式电源(distributed generation，DG)的供电间歇性、实际运行状态下的负荷功率和线路参数存在的波动性等问题，不仅具有受到季度、一天内时段变化影响的时序性，而且在确定时间断面下由于环境的影响也具有高度的不确定性。除此之外，广泛认为是消纳DG和波动负荷必然趋势的柔性互联配电网(flexible interconnected distribution network，FDN)还存在的网损特征问题，如柔性互联装置的换流损耗。这些问题的存在必然会对网损分摊的合理性和精确性提出更高要求。不管是从经济效益角度，还是公平开放的角度，在DG高渗透的FDN背景下如何选择一种公平、合理的网损分摊方法具有很重要的理论和实践意义。

不确定参数的研究现状主要有恒定模型、概率模型、时序模型等。文献[1]采用DG出力与负荷功率最大值或平均值的恒定模型，由于未考虑其随机性和间歇性，结果准确度不高且不符合实际的运行工况。文献[2]考虑了DG、PV在典型日24 个时段的时序特性，应用简单概率模型模拟时段的波动，但未进一步考虑负荷的时序性，使模型整体的精确度下降。文献[3]针对DG、PV与负荷功率选取了几个典型日分别考虑了其时序特性，如各季度的 4 个典型日，虽然能够减少计算量，但仅以固定数据代表各典型日，且未考虑其波动的不确定性，偏离了实际情况。上述文献中的功率模型均未同时考虑时序性和不确定性使潮流计算不够全面和完善。

另外，针对计及不确定性参数的概率潮流算法主要有3种: 点估计法[4](point estimate method，PEM)、解析法[5]、蒙特卡洛模拟法[6](Monte Carlo simulation，MCS)。对于FDN交直流两个系统潮流方程交替迭代形式的交替迭代算法，传统半不变量法直接应用比较困难，而点估计法是将各参数转换为确定性潮流计算，故交替迭代过程中的耦合过程不会对此造成影响，又点估计法中准确度较高且容易计算的三点估计法(three-point estimate method, INT-3PEM)通常作为交直流概率潮流算法的实现方法。

目前，网损分摊方法研究现状均针对于单时段的电力系统。而在系统实际连续运行过程中，运行工况时刻在改变。因此，将网损分摊与概率潮流相结合，研究考虑源网荷时序特性的多时间场景网损分摊成为实际应用中亟待解决的难题。已提出的基本网损分摊方法有：平均网损系数法[7 - 8]、合同路径法[9]、边际网损系数法[10 - 12]、潮流追踪法[13 - 15]等。

综上，网损分摊的研究现状大多针对交流系统，对于FDN的网损分摊鲜有文献进行讨论。本文提出一种兼顾时序特性和不确定性的柔性配电网概率网损分摊模型。首先，通过对源网荷的时序模型和概率分布模型进行梳理，针对时序模型采用基于Nataf逆变换的三点估计法将不确定参数转化为多时间场景下的交直流概率潮流求解。然后，针对网损数据采用网损变化贡献率的分摊方法，通过改进层次分析-熵值定权法确定DG、EV充电桩的网损变化贡献率，将网损变化量基于贡献率分摊给DG和EV充电桩，利用Cornish-Fishe级数拟合分摊电量的概率密度函数。另外，综合各时间场景可得全年分摊电量概率分布曲线；最后，基于改进的33节点柔性网络验证所提方法的有效性。

1 源网荷基于时序特性的概率分布模型

1.1 DG基于时序特性的概率模型

本文主要对光伏DG展开研究，其出力功率受到光照强度影响，且出力时序特性与季节变化密切相关[16]。划分各季度时间场景以建立DG 时序特性概率分布模型，即DG出力历史数据按全年4个季节场景进行划分，选取各季度中的一个典型日共96个时段的数据。如图1所示。

图1 典型DG出力时序特性曲线Fig.1 Typical DG output time series characteristic curve

可将太阳光照强度视为近似服从Beta分布，且光伏DG出力功率也为Beta分布，概率密度函数为[17]：

(1)

式中：Г(·)为伽玛函数；Pg和Pmax分别为光伏DG实际出力和最大出力；α、β为形状参数，可由功率均值μ和标准差σ求得[18]。

(2)

(3)

1.2 负荷基于时序特性的概率模型

同理，常规负荷的时序特性也与时刻、季度密切相关，不同的典型负荷功率时序特性如图2所示。

图2 典型负荷出力时序特性曲线Fig.2 Time series characteristic curves of typical load outputs

可用正态分布模拟负荷的随机性变化，其概率密度函数为：

(4)

式中：P为负荷功率；μP、σP分别为对应统计时段内负荷历史数据的均值和标准差；

1.3 线路参数基于时序的概率模型

实际运行的系统线路阻抗是导体温度的函数，线路参数受温度影响，进而影响系统潮流，而潮流结果的准确评估则是网损计算的基础。而导体温度受线路负载电流、导体的物理特性、外部环境温度、太阳辐射、风速等因素影响。结合式(5)的热平衡方程中与式(6)阻抗的温度修正函数，可确定导体实际工作温度，进一步计算线路实际阻抗。

(5)

(6)

式中：Tc为导体实际温度；T为环境温度；T0为标准温度20 ℃；M为导线质量；Cp为导体比热容；Qs、Qr和Qc分别为导体光照后的吸收热量、辐射散热量和对流散热量[19 - 20]。r、x分别兼顾时序特性和不确定性的柔性配电网概率网损分摊方法T0下的线路阻抗，R、X为Tc时的阻抗；a为T0温度下的电阻温度系数，对于铝a=0.003 6。

对某线路在全年4个典型日的电阻时序特性进行仿真，如图3所示。

图3 线路参数的时序特性曲线Fig.3 Time series characteristic curve of line parameters

另外，假设m表示线路阻抗的随机变量，可视为其服从正态分布[21 - 26]，概率密度函数如式(7)所示。

(7)

2 基于Nataf逆变换的三点估计法概率潮流

基于 Nataf 逆变换的三点估计法(inverse nataf transformation based three-point estimate method, INT-3PEM)进行概率潮流计算[27]，既能分解输入随机变量的相关性，同时求得输出变量的原点矩。基本思路如下：首先，计算独立标准正态空间里的采样点和相应权重，如式(8)—(9)所示。

(8)

式中：μxi、σxi、ξxi,k分别为各随机输入数据的期望、标准差及位置系数。另外，位置系数与权重可根据式(9)求解。

(9)

式中λi,3、λi,4分别为变量xi的偏度和峰度系数。

求出位置系数ξxi,k与权重wi,k后，再将采样点通过Nataf 逆变换到输入变量空间，随后对输出变量H进行 2n+1 次的确定性潮流及网损分摊计算。最后，结合相应的权重求得系统网损及分摊电量的各阶原点矩，如式(10)所示。

(10)

式中：E(·)为期望值算子；N-1(·)为Nataf逆变换算子；Z2n+1中的元素均为标准正态变量的均值；wz2n+1为当所有变量取均值时的对应权重和。

3 考虑网损变化贡献率的网损分摊模型

传统不含DG、EV等新能源的交流配电网，网损分摊对象为电网内部的发电侧和负荷侧，分摊方法有平均网损系数法、潮流追踪法等。而含DG、EV并网的柔性配电网网损分摊研究，本文所提模型的分摊对象仅涉及电网与各DG、EV用户。并考虑如何公平、合理的将新能源用户并网后的系统总网损，在三者间分摊。文献[28]针对含DG的交流配电网，考虑DG的并网位置、容量、渗透率等指标对网损的影响。通过确定DG的网损贡献率，将DG并网引起的网损增量部分根据网损贡献率分摊给各DG用户，分摊思路符合常规实际且易于推广。本文对此分摊方法进行改进，应用于含DG、EV充电桩的柔性配电网。具体思路如下。

(11)

首先，纯交流系统引入了柔性互联装置，一方面，馈线间潮流分布的调节更平滑，提高了消纳DG及波动负荷的能力，降损效果显著[29]。另一方面，柔性化改造增加了电网的规划建设成本。这部分降损效果应奖励给电网的直流规划部门以减少其建设成本，故电网的分摊电量应为交流配电网网损与柔性化导致的网损削减量之和。

(12)

(13)

3.1 网损影响指标体系

第2节中基于Nataf逆变换的三点估计法确定的每个采样值，将FDN的不确定性问题转化为确定性潮流计算。而本节将根据各时间场景下概率潮流计算的网损结果，确定各并网DG、EV用户的网损分摊电量，得到DG、EV充电桩的网损分摊概率密度函数。通过综合96个时间场景得全年网损分摊电量的概率分布函数。建立DG、EV的网损影响指标体系如表1所示。

表1 柔性配电网网损影响指标体系Tab.1 Influence index system of network loss in flexible distribution network

3.2 网损变化贡献率计算

各DG、EV充电桩在实际运行中的不同运行工况下，对网损的影响程度会有所不同。而目前针对DG、EV 对配电网网损造成的影响缺乏合理的量化方法。针对此现状，本文定义了网损变化贡献率的概念，可表征DG、EV对网损的影响程度。首先，分析各影响指标的指标属性并进行预处理；然后，通过层次分析-熵值定权法确定DG、EV充电桩的网损变化贡献率。

1)指标预处理

假设FDN中共接入了n个DG或EV充电桩，指标数量为m个，则构造原始指标数据矩阵X。

(14)

式中xij为第i个随机性设备的第j个原始指标数据。

根据不同的指标属性，将指标数据采用不同的标准化公式进行无量纲转换处理。

(1)正向指标：指标数据值越大，网损影响程度越大；

(15)

(2)逆向指标：指标数据值越小，网损影响程度越大；

(16)

(3)适度指标：指标数据值在一定区间内，网损影响程度越大。

(17)

式(15)—(17)中：xjmax为第j个指标在n个随机性设备中的最大值；xjmin为第j个指标在n个随机性设备中的最小值；q1j、q2j分别为适度性指标j的理想区间边界值。

2)熵权法求客观权重

熵值能够度量指标的不确定性，信息量越大则熵越小。引入熵权法衡量随机性设备不同指标对网损影响的大小，能大幅提高方法的准确性。具体计算步骤如式(18)—(19)所示。

(18)

式中：Ej为n个DG、EV充电桩针对第j个指标的信息熵；x′ij为标准化预处理后的第i个DG或EV充电桩对应第j个指标的数据值。

根据第j项指标信息熵，进一步计算信息熵的差异系数dj和熵权wEj。

(19)

3)层次分析法求主观权重

层次分析法确定主观权重思路是将总目标分解为多准则的若干层次，定性量化指标的网损影响程度，并得出层次的单排序和总排序作为多方案决策。基本步骤为：

(1)确定研究的目标层、准则层以及方案层，建立层次结构模型；

(2)采用一致矩阵法。通常根据1～9位标度法构造判断矩阵，即对同一准则层的评价因素进行两两比较，判断其对于目标层的重要性；

(3)对构造的判断矩阵求其最大特征根及对应特征向量，利用一致性指标、平均随机一致性指标或一致性比率计算矩阵是否通过一致性检验。

4)确定网损变化贡献率

在熵权法确定客观权重wEj及层次分析法确定主观权重wAHPj后，通过式(20)可得各指标综合权重，并由式(21)计算每个随机性设备对FDN网损变化的贡献值。

(20)

(21)

根据DG、EV充电桩的网损变化贡献值，通过式(22)归一化得到其对FDN网损变化的贡献率。

(22)

4 网损分摊模型算法流程

1)输入节点负荷和支路阻抗等基础数据，录入系统拓扑参数以及所需算法参数等。

2)统计DG、EV、负荷及线路参数的历史数据确定各时序特性曲线，并划分时间场景。

3)每个时间场景下通过对应时序曲线的值获取各概率模型参数，进一步得到不确定元件的概率密度函数，并作为该时间场景下概率潮流计算的输入向量。

4)采用INT-3PEM对每个场景进行概率交直流潮流及网损分摊计算。

5)通过Cornish-Fisher 级数拟合得到该时间场景下DG和EV充电桩网损分摊电量的概率密度函数PDF。

6)综合96个时间场景，得到FDN中各DG、EV充电桩的全年网损分摊概率密度分布。

流程图如图4所示。

图4 网损分摊模型算法流程图Fig.4 Flow chart of network loss allocation model algorithm

5 算例分析

5.1 IEEE33柔性配电网算例说明

如图5为改进的IEEE 33节点柔性配电系统。包括33个节点，34条支路。其中，节点12和节点22、节点25和节点29分别通过柔性互联开关SOP1、SOP2进行互联。基准容量为100 MVA。另外，在节点33接入光伏DG，节点15、24接入EV充电桩。系统负荷期望值为原标准系统的负荷值，并按负荷时序特性取其波动值。负荷和线路参数的标准差均为期望值的20%。

图5 改进IEEE 33节点柔性互联配电网Fig.5 Improved IEEE 33 node flexible interconnected distribution network

光伏分布式电源出力时序曲线如图6所示，功率因数均为0.95。

图6 光伏DG出力时序曲线Fig.6 PV DG output time series curves

另外，除发电机节点外，其余节点所接均为波动负荷，系统总负荷时序曲线如图7所示。电动汽车负荷时序曲线如图8所示。线路阻抗时序曲线如图9所示。

图7 总负荷功率时序曲线Fig.7 Total load power time series curves

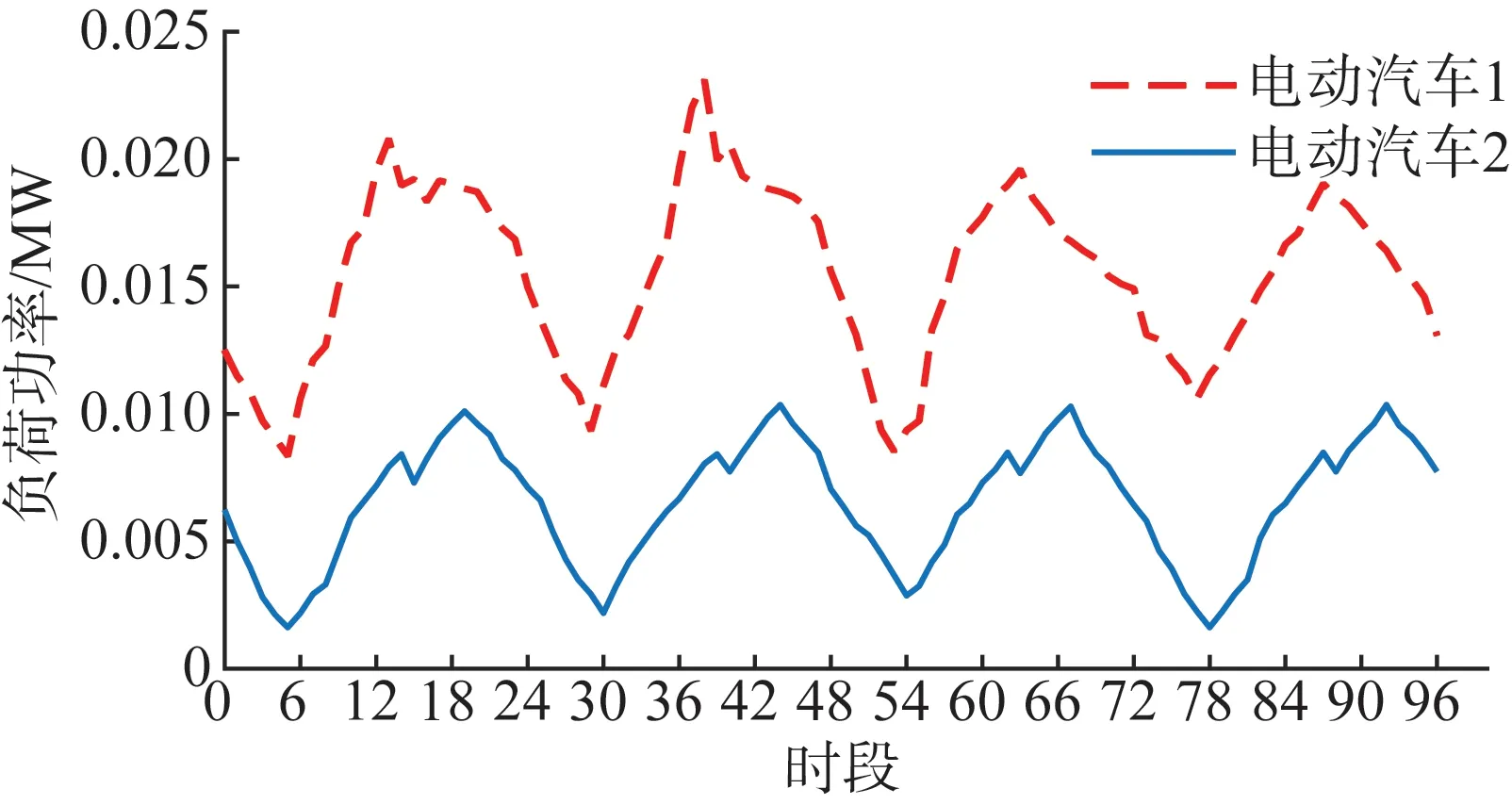
图8 电动汽车负荷时序曲线Fig.8 Electric vehicle load time series curves

图9 线路电阻时序曲线Fig.9 Line resistance time series curves

5.2 IEEE33柔性配电网算例分析

分别采用Nataf分解的三点估计法和蒙特卡洛抽样法，基于各时序波动数据，在96个时间场景下进行概率潮流计算。可得系统典型日网损概率分布曲线如图10所示。

图10 系统全年网损概率分布图Fig.10 Annual network loss probability distribution diagram of the system

同时，在DG、EV未并网时进行一次潮流计算，绘出随机性设备并网前后系统全年网损变化量，如图11所示。

图11 DG、EV并网前后系统全年网损变化量Fig.11 Annual network loss change of system before and after DG and ev grid connection

分析图11可知，由于仅考虑DG、EV的并网状态，而负荷和线路参数的波动条件相同，故网损变化与负荷无关仅与并网DG、EV有关。根据图6和图8可知EV负荷功率远小于DG出力功率，故当DG出力不为0时，系统网损减小，即各季度在时间场景4～22 下，网损的变化量为负。且对比图6，网损变化量与DG出力恰成负相关。综上，DG、EV并网对系统的降损效果将为网损分摊提供理论支撑，即设备的分摊电量也应为负，以奖励其并网。

基于以上潮流计算网损数据进行下一步的网损分摊研究，收集各时间场景下并网DG与EV表1中的网损影响指标数据，根据3.2节层次分析-熵值定权法确定DG、EV的网损变化贡献率。以下针对时间场景15为例，说明网损变化贡献率的计算过程。该场景下的影响指标数据如表2所示。

表2 时间场景15的网损影响指标数据Tab.2 Network loss impact indicator data in time scenario 15

由于除功率因数为逆向指标，其余均为正向指标，故按式(15)—(17)归一化得标准指标数据矩阵X′。按式(18)—(19)采用熵权法可确定各指标的客观权重WE。

(23)

WE=[0.151,0.238,0.309,0.151,0.151]

(24)

另外，层次分析法确定指标主观权重WAHP的过程如下。

对受测试FDN的网损影响因素进行分析，建立网损影响程度评价指标层次分析体系，如图12所示。选取表1中5项指标及规划、运行两类评价因素，对网损影响程度进行综合评价。首先，基于电网实际运行经验比较各指标的的重要程度对各指标进行概化分级赋值，建立柔性配电网网损影响机理的判断矩阵，如表3—5所示。

图12 网损影响程度评价指标层次分析体系Fig.12 AHP system of network loss impact evaluation index

表3 准则层-评价因素对网损影响判断矩阵Tab.3 Criterion layer-judgment matrix of influence of evaluation factors on network loss

表4 方案层-指标对规划影响判断矩阵Tab.4 Scheme level-index impact judgment matrix on planning

表5 方案层-指标对运行影响判断矩阵Tab.5 Scheme level-index impact judgment matrix on planning scheme level-index impact judgment matrix on operation

然后，采用随机一致性比率CR检验矩阵的一致，最后求得各指标的主观权重WAHP。

WAHP=[0.179,0.314,0.182,0.163,0.163]

(25)

结合式(24)和式(25)，由式(20)可确定指标综合权重W。

W=[0.131,0.361,0.271,0.119,0.119]

(26)

根据式(21)、式(22)计算每个随机性设备对受测试FDN的网损变化贡献率λ，结果如表6所示。另外，由图10可知，时间场景15下系统网损期望值为1.392 kW。另计算DG、EV未并网时，该时间场景下系统网损值为1.831 kW。网损变化量为-0.439 kW，应由并网的随机性设备按网损变化贡献率进行分摊，各设备的分摊电量(时间为1 h)如表6所示。

表6 时间场景15下DG、EV分摊电量Tab.6 Shared power of DG and EV under time scenario 15

分析上表，在该时间场景下，DG、EV并网使系统总网损减小了0.439 kW，即网损变化量为负；根据网损变化贡献率可知DG对网损的影响最大，其次是EV2充电桩，影响最小的为EV1充电桩；另外，三者的分摊电量为负，则表示由于降损作用应奖励DG、EV的并网。

根据上述网损分摊模型对96个时间场景分别进行分摊计算，综合各时间场景可得受测试FDN全年DG和EV的分摊电量如图13所示。

图13 受测试FDN全年DG、EV1、EV2网损分摊电量Fig.13 Annual DG, EV1, EV2 network loss allocation of tested FDN

由图13可知，DG出力不为0时，系统网损减少，故DG、EV充电桩分摊电量均为负值，与理论推导一致。且每个时间场景下DG与EV充电桩的分摊电量大小与其网损影响指标的数据值有关，具体过程如以时间场景15为例的网损分摊所示。

1)是否考虑时序特性的分摊结果对比

对比本文兼顾时序特性和不确定性的概率网损分摊模型的精确度，采用DG出力为季度平均值的恒功率模式，且不考虑负荷和线路参数的波动情况进行概率网损分摊，得各季度DG、EV充电桩的网损分摊概率分布，如图14所示，与是否考虑时序特性两种情况下，随机性设备各季度的网损分摊电量对比，如表7所示。

图 14 不考虑时序特性DG、EV1、EV2分摊电量概率分布Fig.14 Probability distribution diagram of DG/EV1/EV2 shared electricity without considering time series characteristics

表7 DG、EV各季度考虑时序特性的网损分摊电量对比Tab.7 Comparison of grid loss allocation and power consumption of DG and EV considering time series characteristics in each quarter

分析可知，若不考虑时序特性，无法全面考虑系统实际运行中某些恶劣的运行状态，其网损分摊奖惩策略的应用参考价值有待提高。另外，通过潮流计算可求得不考虑源网荷时序特性时，系统4个典型日总网损电量为115.4 kWh。而考虑源网荷时序特性时系统4个典型日总网损电量为133.17 kWh，两者误差17.77 kWh，累计一年，网损误差可达1 621.51 kWh。综上，若不考虑系统实际运行时DG出力、负荷波动以及线路阻抗的时序特性，将使系统网损电量、各DG和EV充电桩的分摊电量出现较大误差，对系统的安全稳定运行、可靠性及经济性造成影响。

2)SOP及DG、EV接入的网损对比

同样以时间场景15为例，分别对IEEE33纯交流系统，以及分别接入柔性互联装置和DG与EV后的系统总网损概率分布进行仿真，如图15所示。分析可知，纯交流系统引入柔性互联装置后线损期望值显著降低且波动方差减小；而DG接入后线损期望值减小，但其增大了波动方差。

图15 时间场景15下不同系统状态的网损概率分布Fig 15 Probability distribution of network loss in different system states under time scenario 15

3)3PEM和MCR概率潮流计算对比

为验证本文所概率网损及其分摊方法模型的计算精度，将该系统通过蒙特卡洛模拟法进行概率潮流计算，对比结果与计算速度。设置MCR模拟法抽样数N为500。考虑随机变量时序特性对柔性互联配电网进行仿真。96个时间场景下两种方法计算结果及计算用时如表8所示。

表8 3PEM与MCR方法网损计算结果对比Tab.8 Comparison of network loss calculation results between 3PEM and MCR methods

由图10可知，三点估计法与蒙特卡洛模拟法概率潮流计算所得网损结果差距很小，计算所得96个时间场景的网损均值平均误差仅为0.000 4，精度可满足电力系统网损计算的需求。在计算精度近似的条件下，三点估计法能极大地减少计算所需时间，更适用于大规模多时段的柔性配电网的概率网损计算。

5.3 实际配电网算例说明

为验证本文所提线损分摊模型推广应用的实际意义，针对东莞松山湖柔性配电网“2-1”过渡接线形式拓扑的实际算例进行仿真，如图15所示。包括16个节点，15条支路。其中，节点5和节点16通过柔性互联开关SOP1、SOP2进行互联。基准容量为100 MVA。另外，在节点5接入光伏DG，节点7、13接入EV充电桩。各时段系统负荷根据期望值并按负荷时序特性取其波动值。负荷和线路参数的标准差均为期望值的20%。

光伏分布式电源出力时序曲线如图16所示，功率因数均为0.95。另外，除发电机节点外，其余节点所接均为波动负荷，系统总负荷时序曲线如图17所示。系统总负荷时序曲线如图18所示。

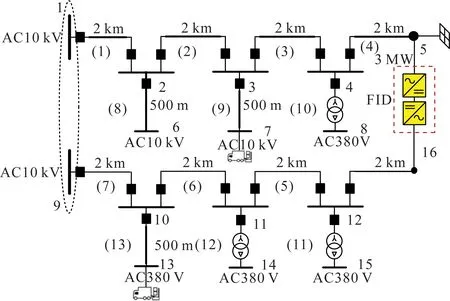
图16 东莞松山湖柔性配电网拓扑Fig.16 Topology of Dongguan Songshanhu flexible distribution network

图17 光伏DG出力时序曲线Fig.17 PV DG output timing curve

图18 系统总负荷时序曲线Fig.18 Time series curve of total system load

5.4 实际柔性配电网算例分析

在各时间场景下，根据柔性配电网实际运行工况进行概率潮流计算，得到典型日概率网损分布如图19所示。

图19 典型日概率网损分布图Fig.19 Typical daily probability network loss distribution diagram

分析上图可知，在各季度典型日，随着DG出力增大，系统网损略有减小。

同时，针对不同时间场景，收集并网DG、EV的网损影响指标数据，利用层次分析-熵值定权法计算其网损变化贡献率。以下为时间场景39的网损分摊计算过程。

根据层次分析-熵值定权法由式(15)—(10)确定该时间场景下各指标的综合权重。

W=[0.141 4,0.339 3,0.255 1,0.132 2,0.132 2]

(27)

由式(21)—(22)计算DG、EV的网损变化贡献率。再根据随机性设备并网前后的网损变化电量差值0.602 862 4 kWh(t=1)，按网损变化贡献率由各随机性设备分摊，结果如表9所示。

表9 时间场景39的网损影响指标数据Tab.9 Network loss impact indicator data in time scenario 39

分析表9可知，在时间场景39下，DG、EV的并网降损0.439 kW，由于网损变化量为负，故应奖励其并网，即三者的分摊电量为负；根据网损变化贡献率λ可知，对网损影响程度由大到小分别是DG、EV2充电桩、EV1充电桩。时间场景39下DG、EV分摊电量如表10所示。

表10 时间场景39下DG、EV分摊电量Tab.10 DG and EV shared power under time scenario 39

同理，根据上述过程分别对96个时间场景进行网损分摊计算。得实际FDN全年DG和EV的分摊电量如图20所示。

图20 实际FDN全年DG、EV1、EV2网损分摊电量Fig.20 Actual FDN annual DG/EV1/EV2 power loss allocation

6 结论

本文针对DG出力、常规负荷及EV负荷功率、线路阻抗波动的时序特性与概率模型进行研究，在此基础上构建了兼顾时序特性和不确定性的柔性配电网概率网损分摊模型，将网损变化量基于网损变化贡献率分摊给并网DG、EV。

1)与不考虑各随机变量不确定性的传统柔性配电网相比，本文构建的时序特性和不确定性模型能更真实地反映配电系统的运行情况，更准确地评估配电网实际的运行工况。

2)本文采用的INT-3PEM结合FDN进行交直流概率潮流计算，在算法上优于半不变量、蒙特卡洛等概率潮流算法，在背景上更符合强波动性高渗透率的配电网发展现状。

3)在网损分摊算法上，建立了一套网损影响指标体系，且指标易获取、易量化，有较强实用性。提出的层次分析-熵值定权法能确定DG、EV并网后网损变化贡献率，衡量其对配电网网损的影响程度。网损分摊结果可提供经济运行信号，指导DG、EV的降损并网。