考虑满意度的两阶段DEA固定成本分摊方法

张 冉，冉 伦，杜 涛,4，李金林

(1.中国光大集团博士后工作站，北京 100033；2.清华大学五道口金融学院博士后流动站，北京 100083；3.北京理工大学管理与经济学院，北京 100081；4.延安大学经济与管理学院，陕西 延安 716000)

1 引言

数据包络分析(Data Envelopment Analysis, DEA)方法是用来评价具有多项投入和多项产出的决策单元(Decision Making Units, DMU)相对效率的方法，最早由Charnes等[1]提出。由于固定成本可以作为一项投入要素，因此很多学者采用DEA方法来研究固定成本的分摊问题。这类问题有着广泛的应用背景，如集团公司为各子公司建立统一的信息系统所需要的成本如何在各子公司进行分摊，银行系统为各分行建立统一的交易系统所需要的花费如何分摊等等。

近年来，DEA方法已被广泛地应用到固定成本的分摊问题中，并取得了诸多的研究成果。Cook和Kress[2]首次将DEA方法应用到固定成本分摊问题中，将待分摊的成本看做一种新的投入要素，以成本分摊后各DMU的效率不变和Pareto最小性为准则，提出了确定成本分摊方案的方法。Beasley[3]以最大化所有DMU的效率和的平均值为目标，建立了一个非线性的DEA模型。李勇军和梁樑[4]证明了任何DMU在自我设计方案时，都能找到一组分摊方案使其自身的相对效率值达到最大值1。并给出了在一组公共权重下，可以使得组织整体和各DMU效率同时达到最优的成本分摊方案集。进而利用Nash讨价还价博弈模型求得唯一的分摊方案。随后，李勇军等[5]将DEA方法与联盟博弈相结合，定义了联盟博弈的特征函数,提出了基于核仁解的固定成本分摊模型。Li Yongjun等[6]定义了DMU对分摊方案的满意度，以最大化最小的满意度为目标函数建立DEA成本分摊模型，得到唯一的成本分摊方案。Du Juan等[7]提出了一种交叉效率的方法，设计了一个迭代过程得到最优的成本分摊方案。其他的利用DEA方法进行成本和资源分摊的研究可参见Cook和Zhu[8]、雷西洋等[9]。以上这些文献主要集中在决策单元只有一个生产阶段的情况下采用DEA方法进行固定成本分摊。

实际生活中，决策单元可能存在两个(或多个)生产阶段，其中第一个阶段的产出又作为第二个阶段的投入。例如银行系统中，第一阶段投入人力等资源获得客户存款，第二阶段再用这些存款进行放贷，最终获得收益。这样的两阶段DMU的固定成本分摊不仅要考虑固定成本在各DMU之间的分摊，还要考虑到阶段间的成本分摊。目前，两阶段DEA方法的研究较为丰富，如Kao和Hwang[10]、Chen Yao等[11]和毕功兵等[12]，但是利用两阶段DEA方法进行固定成本分摊的研究很少。孙玉华和曾庆铎[13]考虑两阶段网络DEA，选取两阶段效率的乘积作为DMU的整体效率，通过最大化DMU整体的效率建立DEA模型。在设计成本分摊方案时考虑DMU各阶段存在博弈的情况，建立讨价划价模型确定DMU和各阶段的分摊成本。然而，他们的研究只是简单的将李勇军[4]的方法从单阶段系统平移到两阶段系统中，并没有给出该方法适用于两阶段串联系统的证明，也没有任何的数值算例，使得其研究缺乏理论依据。Yu等[14]选取加法形式的效率，选取两阶段效率的加权和作为DMU的整体效率。将Du Juan等[7]提出的交叉效率的方法应用到两阶段串联系统中。但很可惜，他们的研究并没有证明交叉效率迭代方法在两阶段串联系统可以得到唯一的最优解。而且，数值算例的结果也显示最终各DMU两阶段的效率并没有达到最优。

总的来说，现有的考虑两阶段DEA进行固定成本分摊的研究都是简单的将单阶段系统的固定成本分摊方法平移到两阶段系统中。无论是孙玉华和曾庆铎[13]，还是Yu等[14]都没有给出方法适用性证明，缺乏理论依据。与这些研究不同，本文将Li Yongjun等[6]的研究拓展到两阶段生产系统中，证明了该方法的适用性。然后，进一步考虑了两阶段存在共享投入的情况下如何进行固定成本分摊。具体地，选取Chen Yao等[11]提出的加性两阶段DEA整体效率，以最大化当前DMU整体效率为目标函数建立DEA成本分摊模型。首先证明了每个DMU都可以找到至少一种成本分摊方案使得其自身整体效率和两阶段效率均为1，即Pareto有效。然后证明了存在至少一种成本分摊方案，使得在一组适当的公共权重下，所有DMU的整体效率和两阶段的效率均是Pareto有效的，并给出了这样的有效成本分摊方案集。在这个方案集中，考虑各DMU各阶段对分摊方案的满意度，以最大化最小的满意度为目标，建立最终的DEA成本分摊模型，可以得到一组最为公平的成本分摊方案。将问题拓展到两阶段存在共享投入的生产系统中，这些性质定理同样成立。数值算例部分选取某银行的27个分行的投入产出数据，将本文提出的方法与Yu等[14]的研究结果进行了对比，指出了本文提出方法的优越性。然后，将投入数据作为共享投入处理，进一步给出了考虑共享投入下的固定成本分摊结果，并与未将投入视为共享投入的情况下得到的结果进行了对比。利用本文的方法进行固定成本分摊能够保证各分行的整体和阶段效率均为Pareto有效，并且分摊方案充分考虑了各DMU两阶段的满意度，有利于分摊方案的实际执行。

2 考虑固定成本分摊的两阶段效率评价模型

s.t.

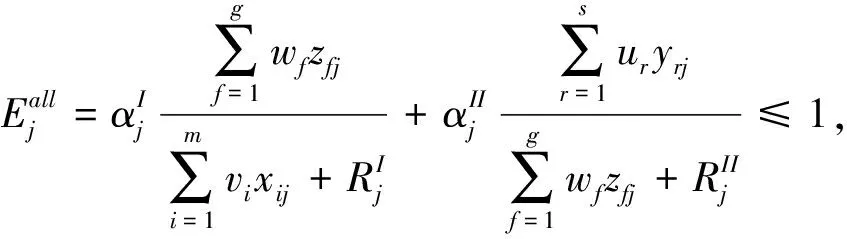
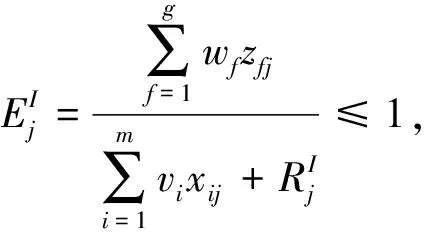
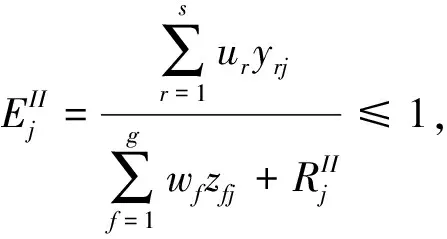
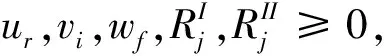
(1)

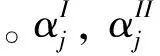
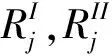
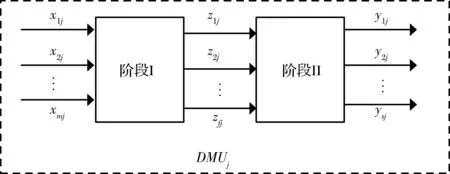
图1 两阶段DMU系统

在DEA理论中，当被评价决策单元的相对效率值为1的时候，称其为Pareto有效。

定理1模型(1)中，对于任意的DMUd，都存在至少一种成本分摊方案，使得其自身整体效率和两阶段的效率同时达到Pareto有效。

证明：对于任意DMUd，令：

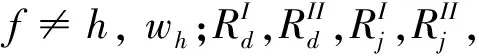
这是因为ξ满足模型(1)的所有约束条件：

定理1说明了每个DMU从自身的角度出发，都可以找到至少一组分摊方案使其自身无论是整体效率还是阶段效率都达到帕累托有效。但是从每个DMU自身角度出发得到的成本分摊方案不能保证其他DMU也达到Pareto有效，因此需要寻求一种分摊方案集，使得所有DMU的两阶段效率和整体效率能够同时达到Pareto有效。

定理2在模型(1)下，至少存在一种成本分摊方案，使得在一组公共的权重下，所有DMU的两阶段效率和整体效率同时达到Pareto有效。

证明：同样地，令：

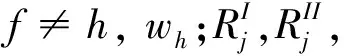
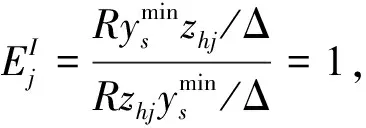
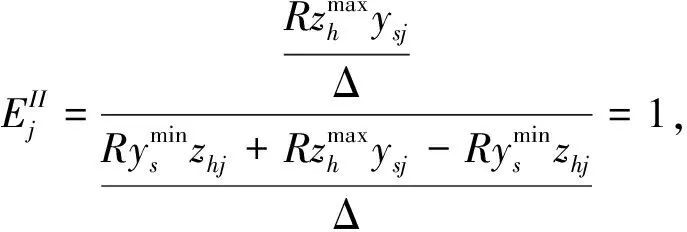
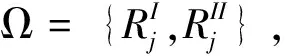
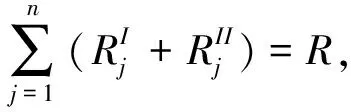
(2)

证明：由定理2可知，存在一组共同的权重使得所有DMU的两阶段效率和整体效率均为1，假设这组公共权重为(vi,ur,∀i,r)，则有：

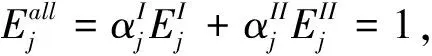
(3)

显然等式组(3)可以转化为等式组(2)，因此基于(2)的成本分摊方案集Ω，能够保证在一组适当的公共权重下使得所有DMU的整体效率和阶段效率均为1。

定理1至定理3构成了本文的两阶段DEA固定成本分摊方法的理论基础。它们保证了在一组适当的公共权重下，决策者可以找到至少一组成本分摊方案，使得所有DMU的阶段效率和总效率都达到最优，同时系统的总效率也达到最优。定理3中给出的有效成本分摊集中的任何一个成本分摊方案，都能够找到一组合适的公共权重，使得所有DMU的两阶段效率和总效率都达到最优。

问题(1)是一个分式规划，通过Charnes-Cooper变换将其转换成线性规划问题，令：

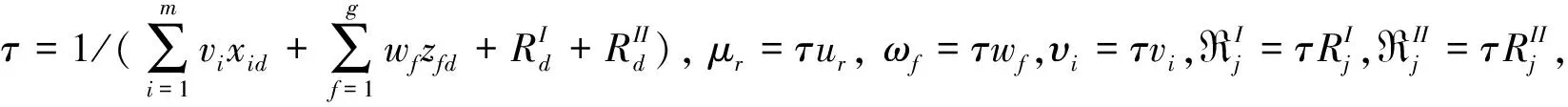
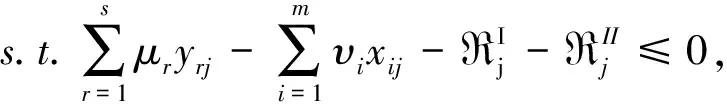
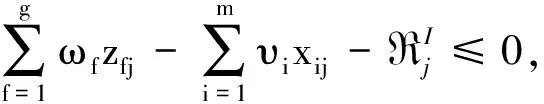
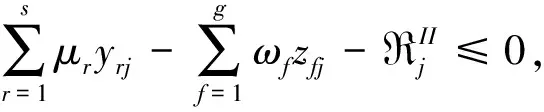
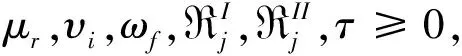
(4)

3 考虑满意度的两阶段固定成本分摊模型

由定理2可知问题(1)存在唯一的最优目标函数值1，但使得其目标函数值最优的解可能存在很多。即可能存在多种权重组合和成本分摊方案，使得DMU的最优效率值为1。为了寻求一组确定的成本分摊方案，考虑各DMU对成本分摊的公平感知，在有效成本分摊方案集中寻找一组最为公平的分摊方案。

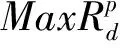
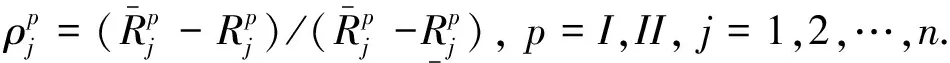
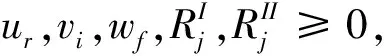
(5)

模型(5)有效地将DMU各阶段的DEA相对效率与其对分摊方案的满意程度结合起来。由于采用的是Pareto有效的成本分摊方案集作为约束条件，因此，可以保证由此得到的分摊方案可以使所有DMU整体和两阶段效率能够在一组公共的权重下同时达到Pareto有效。由模型(5)得到的分摊方案充分考虑了各DMU各阶段对分摊结果的满意度，使得分摊方案更加公平。

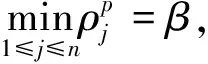
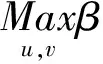
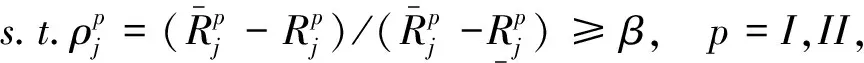
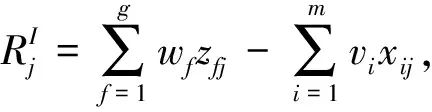
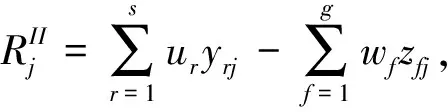
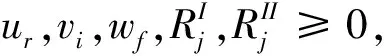
(6)

这里我们把n个DMU拆分成2n个DMU，即把每个DMU的每个阶段都当做一个DMU，使其最小的满意度最大。模型(6)转化为：

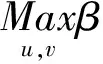
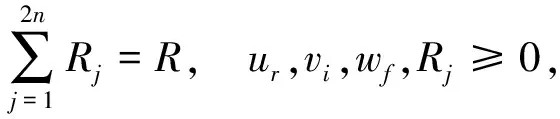
(7)

则上述模型中ρj,j=1,2,…,n,是DMUj第I阶段的满意度，ρj,j=n+1,n+2,…,2n,是第II阶段的满意度。Rj,j=1,2,…,n,是DMUj第I阶段的固定成本分摊量，Rj,j=n+1,n+2,…,2n,是DMUj第II阶段的固定成本分摊量。设计以下步骤获得模型(7)的最终解。

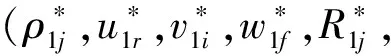
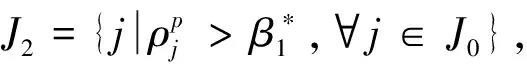
步骤3：令l=l+1,求解下面的模型：

…

ρj≥β,j∈J2l-3,j∈J2l-2

ur,vi,wf,Rj≥0, ∀i,r,j

(8)

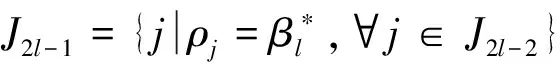
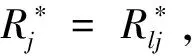
上述方法可以保证在有限的迭代过程后得到唯一的最优解。得到的解是使得各DMU各阶段的满意度差别最小的，保证了分摊结果的公平性。同时由于所有的计算过程都是以有效的成本分摊方案集为约束条件的，因此得到的分摊方案可以使得在一组公共的权重下，所有的DMU和各阶段效率都是Pareto有效的。

4 考虑两阶段存在共享投入的情况

现实生活中，这些两阶段生产系统往往具有一些共同的投入资源，且该资源很难被清楚地划分到两个阶段的生产过程中。如Chen等[16]认为银行的存款阶段需要人员、信息技术、固定资产等投入，同样，在贷款阶段也需要人员、信息技术和固定资产等投入。而且，这两个阶段的共同投入很难划分清楚。因此，考虑共享投入后再依据效率来进行固定成本的分摊更加符合实际，更具有指导意义。因此，将所研究的两阶段生产系统进行拓展，考虑对如图2所示的决策单元进行固定成本分摊。

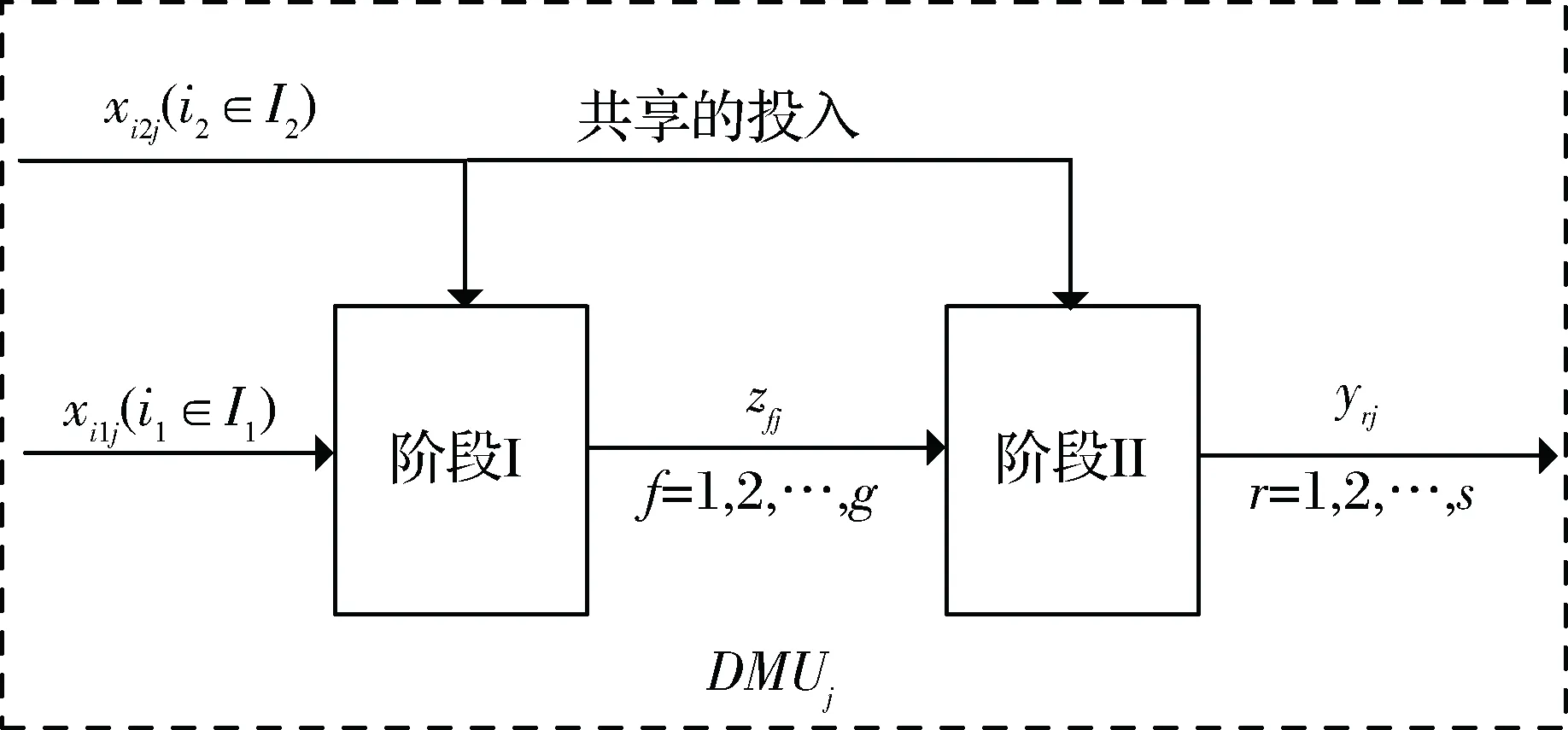
图2 具有共享投入的两阶段DMU系统

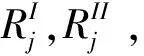
对于每个DMUj，其共享的投入在两阶段之间的比例βi2j在理论上的取值范围是[0,1]，但当βi2j取0或1的时候代表项投入资源要么全部用于第I阶段生产，要么全部用于第II阶段的生产，因此就不是共享的投入了。而且，在实际中，每个DMU每项共享的投入其在两阶段的占比会有一个大概的取值范围，参照Chen Yao等[16]的研究，本文设置为[Li2j,Ui2j]。对于任意的DMUd，最大化其整体效率可以建立以下模型：

s.t.

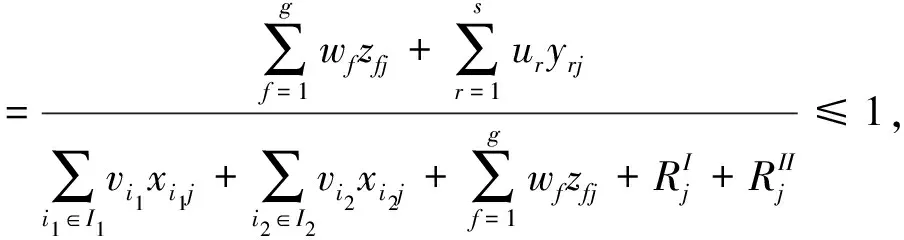
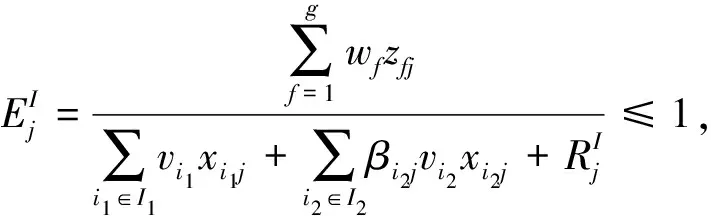
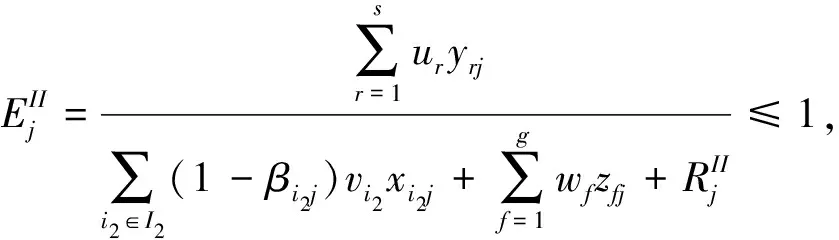
Li2j≤βi2j≤Ui2j, ∀i2∈I2,j=1,2,…,n

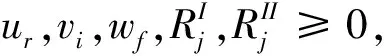
(9)

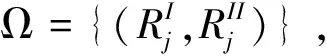
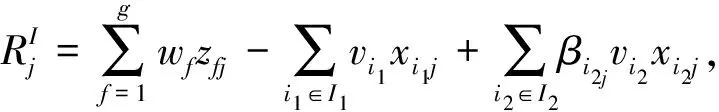
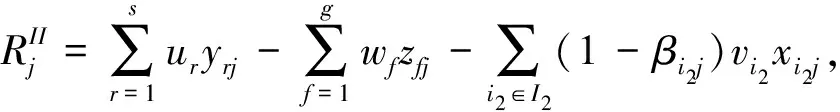
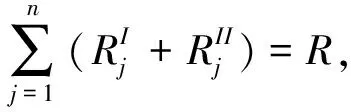
Li2j≤βi2j≤Ui2j, ∀i2∈I2, ∀j

(10)

实际上，由于阶段I和阶段II都参与固定成本的分摊，因此固定成本也是一种共享的投入。可以说，不考虑共享投入是一种特殊情况，共享投入的模型更加具有一般化。因此，是否考虑共享投入不会影响到本文几个定理的结论。即对于任意的决策单元，总是能找到至少一种成本分摊方案，使得其自身整体效率和两阶段的效率同时达到Pareto有效。并且当对所有决策单元采用一组合适的公共权重来进行效率评价时，能够找到至少一组成本分摊方案使得所有决策单元的整体效率和两阶段的效率同时达到Pareto有效。

s.t.

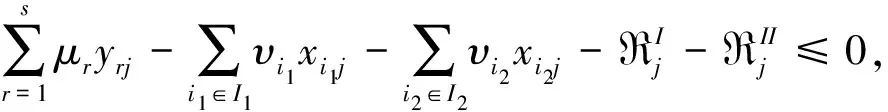
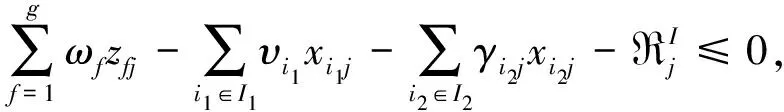
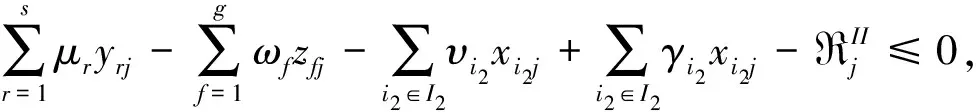
υi2Li2j≤γi2j≤υi2Ui2j, ∀i2∈I2,j=1,2,…,n

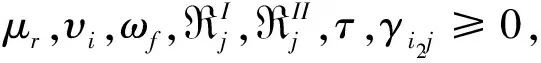
(11)

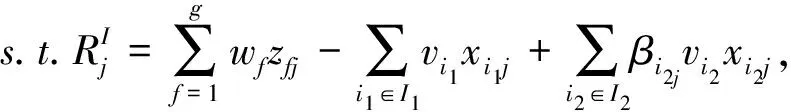
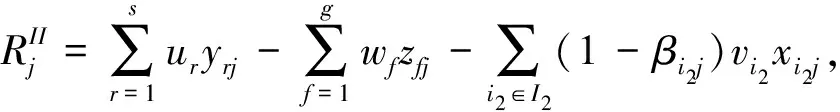
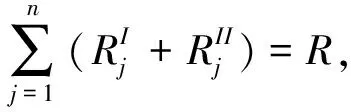
Li2j≤βi2j≤Ui2j, ∀i2∈I2, ∀j

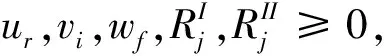
(12)

同样可以采用第3节中的算法求解模型(12)，由于采用的是Pareto有效的成本分摊方案集作为约束条件，因此，可以保证由此得到的分摊方案可以使所有DMU整体和两阶段效率能够在一组公共的权重下同时达到Pareto有效。

5 算例分析

为了方便与Yu等进行对比，本文同样采用Chen Yao等[16]使用的银行的相关数据对上述建立的考虑满意度的两阶段固定成本分摊模型进行检验。数据中的27个分行隶属于同一个银行，并且各自独立运营。每个分行都以固定资产、IT投入和员工作为第一阶段的投入来获得顾客存款。然后在第二阶段利用这些存款作为投入，以贷款回收比例和利润作为产出。

假设银行总行要将100万美元的某项固定成本分摊到27个分行。利用本文提出方法，首先算出每个DMU各阶段固定成本均摊的最大值和最小值，然后建立模型(5)，采用本文改进的算法来求解，利用Matlab编程，程序计算1次就满足了n1+n2+…+nl≥m+g+s，即满意度最小的决策单元的数量大于6，这时迭代停止，得到的最终的两阶段成本分摊结果、满意度和公共权重下的效率如表1所示：

表1中第2至5列分别显示了各DMU两阶段需要分摊的固定成本的最小值和最大值。所有DMU第I阶段需要分摊的成本的最小值都是0。而对于DMU的阶段II，只有几个分行的最小值是0，大多数分行的最小值都大于0。这意味着大多数分行的阶段II势必要比阶段I分摊更多成本。同样，通过对比各DMU两阶段需要分摊的最大的成本也可以看出，阶段II需要分摊的最大值也普遍比阶段I高。这与通过对比最小值得到的结论是一致的。第6和7列是模型最终算得的各DMU两阶段需要分摊的固定成本的最优值，所有DMU两阶段的固定成本分摊的总量为R=100。在这个分摊方案下，可以保证DMU各阶段对分摊方案的最小满意度最大化。第8和9列即是各DMU各阶段对该分摊方案的满意度。其中第 6，8，9，10，11，14，15，16分行的阶段I和第3，14，24分行的阶段II对分摊方案的满意度最低，为0.54。其他分行的两阶段对分摊方案的满意度均高于0.54，最大的满意度为第20分行的阶段II0.75。满意度最小的决策单元的个数为11大于6，因此模型计算1次即终止。最后3列验证了在这组公共权重下，各DMU按照上述结果对各阶段进行固定成本分摊，可以保证所有DMU的整体和阶段效率均为Pareto有效。通过对比第8列和第9列数据还可以发现，同一个DMU在两个阶段之间对固定成本的分摊方案的满意度也很相近。因此，该分摊方案是较公平的，切实可行的。

接下来，将利用本文提出的方法得到的结果与Yu等[14]的结果进行对比，见表2。

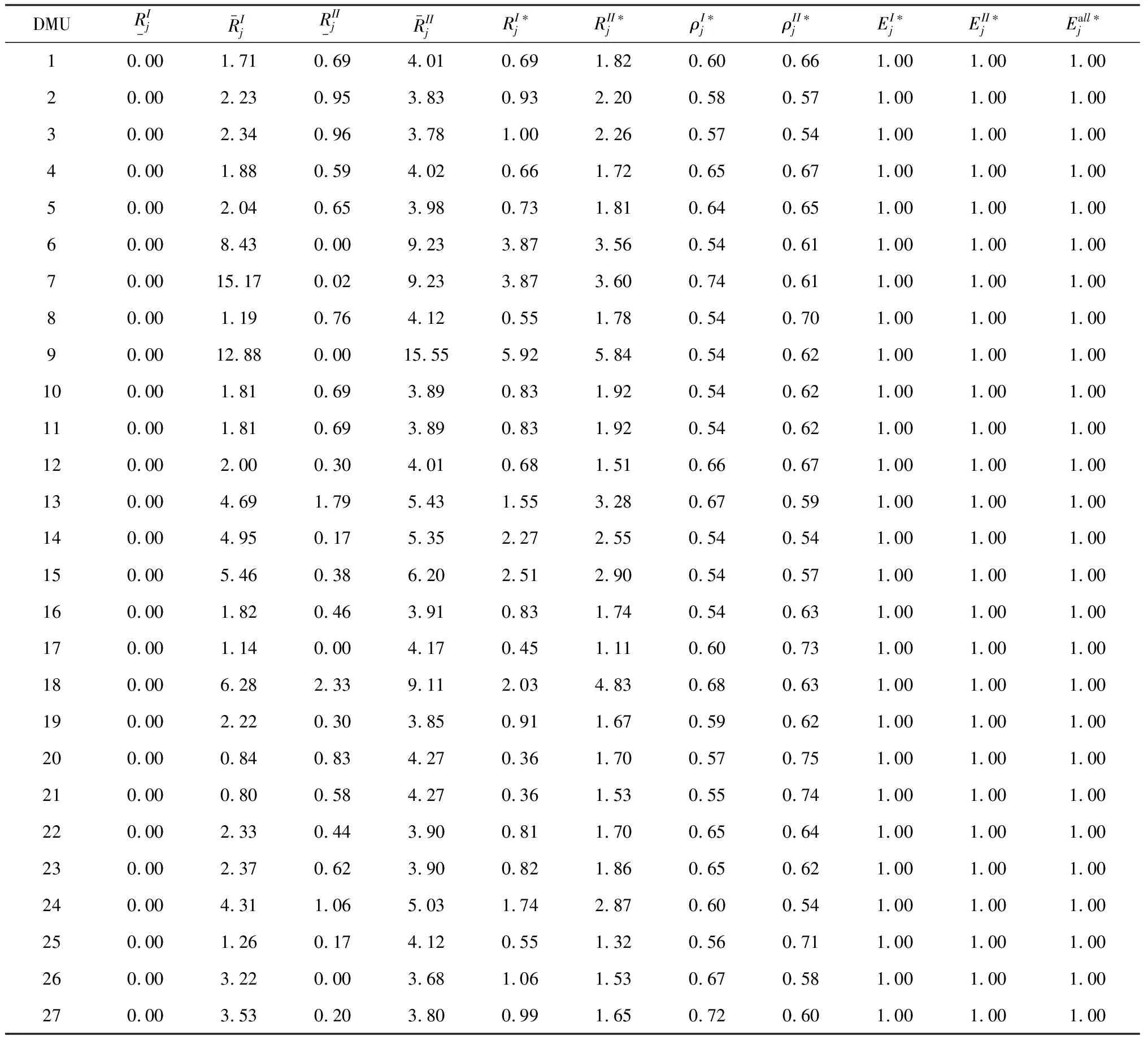
表1 本文方法固定成本分摊的相关结果

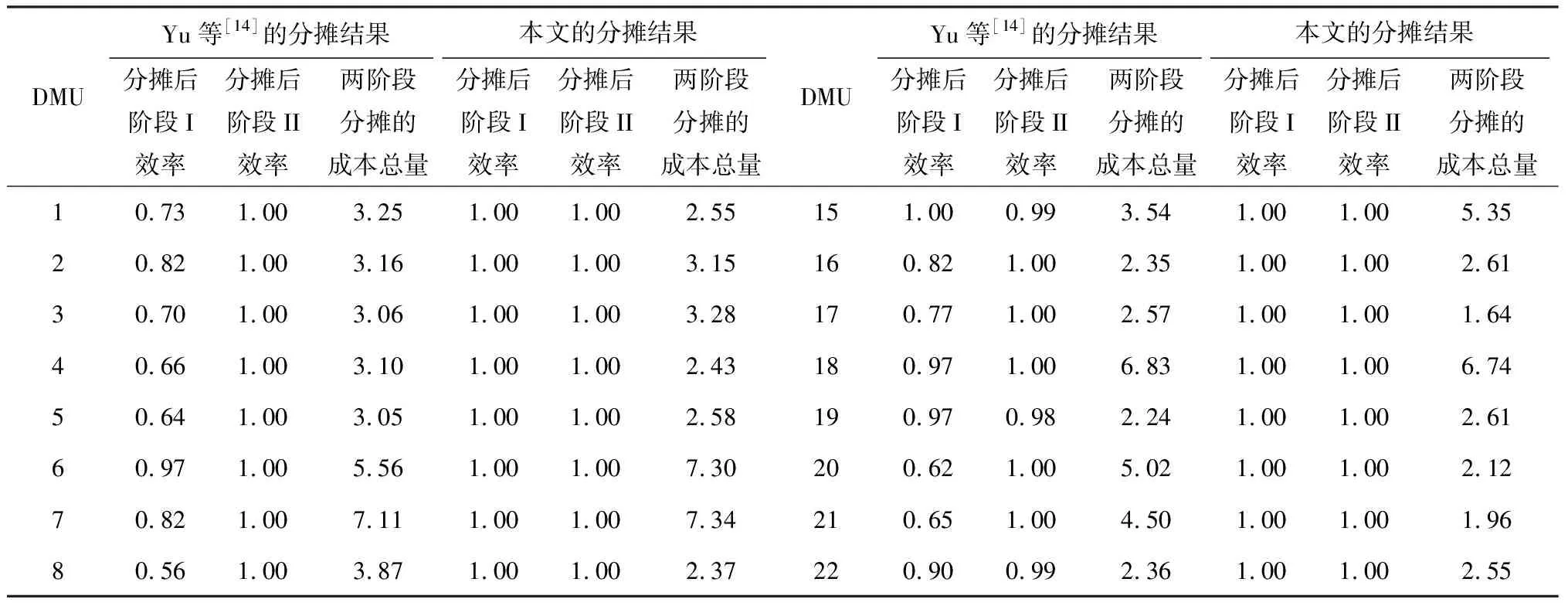
表2 本文和Yu等[14]分摊结果对比

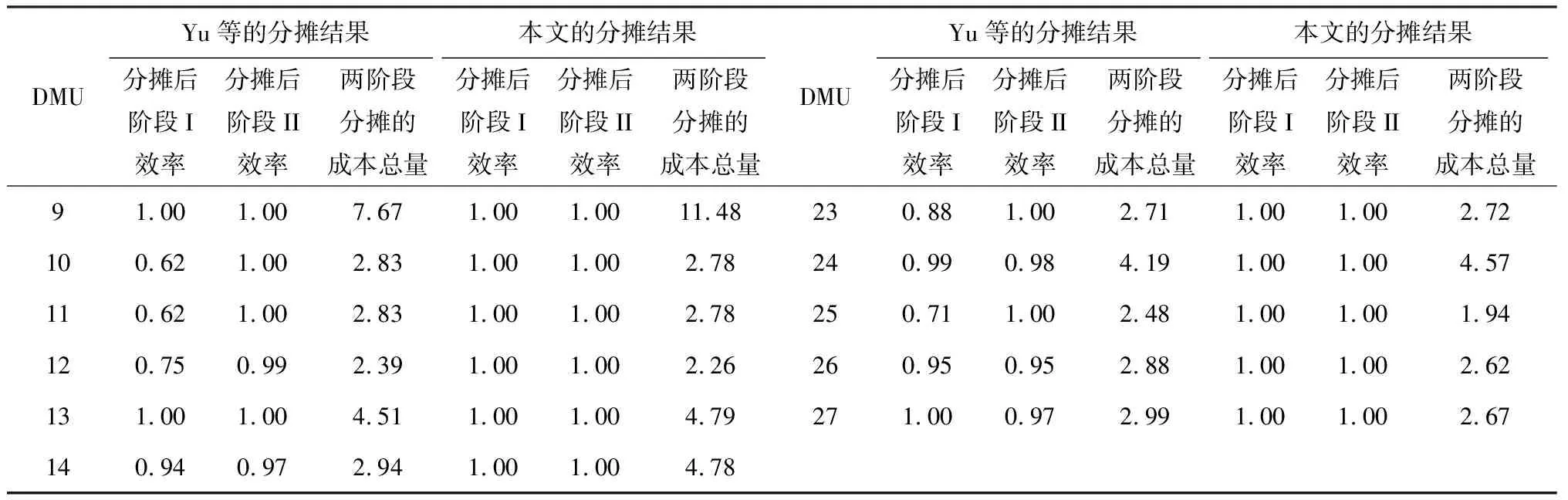
续表2 本文和Yu等分摊结果对比

表2中Yu等[14]的结果是通过两阶段DEA交叉效率的方法得到的。本文则是采用公共权重对所有DMU进行效率评价和成本分摊。由于Yu等[14]文中只给出了DMU整体分摊的成本量和分摊后两阶段的效率，因此，这里仅对这几项结果进行对比。通过对比DMU整体的成本分摊量可以看出，两种方法的分摊结果存在一定的差别。但从整体的分摊趋势来看，两种方法的结果是一致的。如第7、9和18分行的成本分摊量均高于其他分行；第12、16和17分行的成本分摊量均低于其他分行等。通过对比分摊后两阶段的效率，可以明显看出，本文提出的方法能够保证所有的DMU两阶段的效率都达到最优值1。而Yu等[14]在分摊后两阶段的效率并非都达到了最优值1，这也说明了该方法存在一定的改进空间。因此，从分摊后各DMU的效率来看，本文提出的方法优于Yu等[14]的方法。

实际生活中，银行的存贷款两阶段都需要固定资产、IT投入和员工。因此，这些投入是两阶段共享的资源，而且很难进行精确的划分。针对这种情况，本文参照Chen Yao等[16]的设置，假设不同分行同一种共享投入资源比例的上下界是相同的，设定这三项共享的投入资源用于阶段I的比例区间分别为0.4≤βF≤0.6，0.25≤βI≤0.75和0.55≤βE≤0.75。利用第4节中的方法来分摊100万美元固定成本。将是否作为共享投入处理得到的结果进行对比，如表3所示。

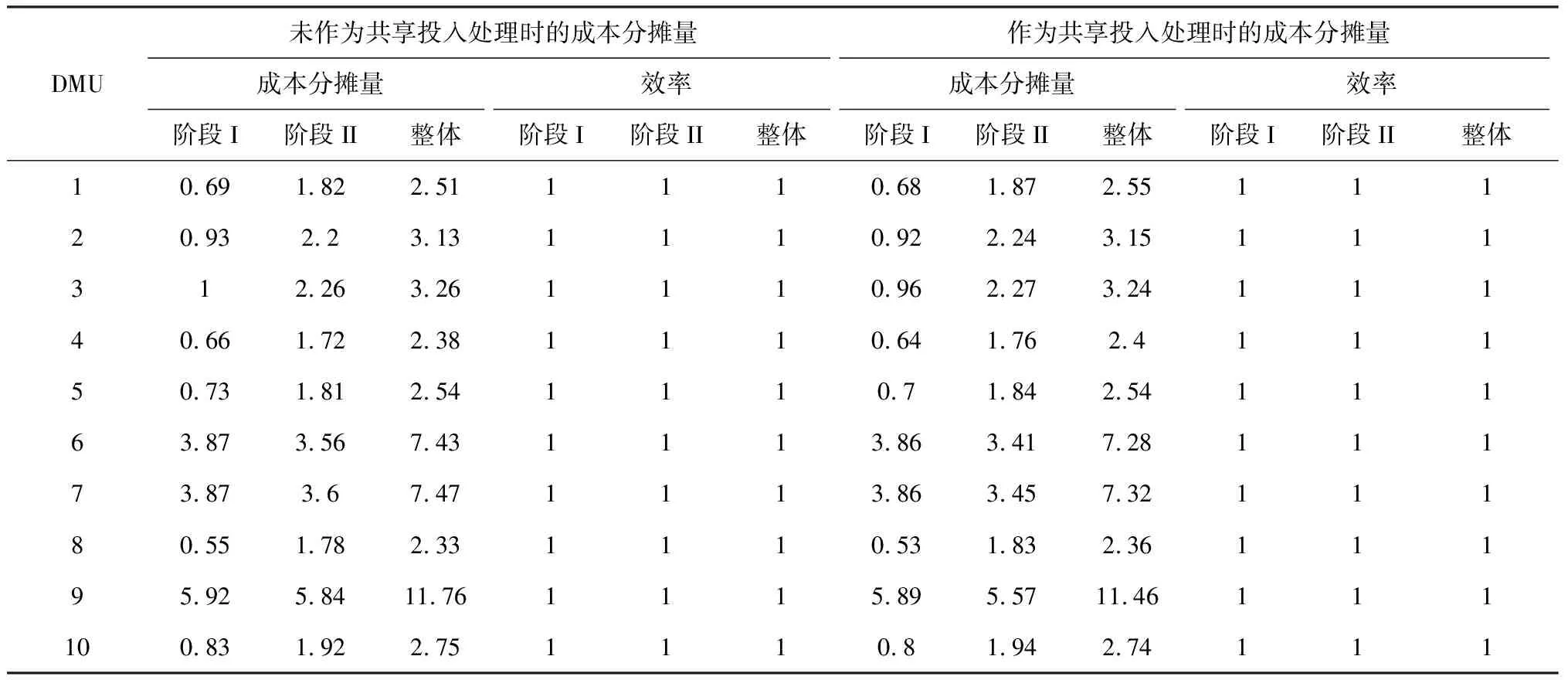
表3 是否视为共享投入的结果对比

表3中第2至7列是未将固定资产、IT投入和员工作为共享投入处理得到的结果。第8至13列是将它们作为共享投入处理得到的结果。可以看出，无论是否将它们作为共享投入，最终得到的结果，各DMU整体及其两阶段的公共权重效率都为1。考虑共享投入的情况下，所有决策单元阶段I的

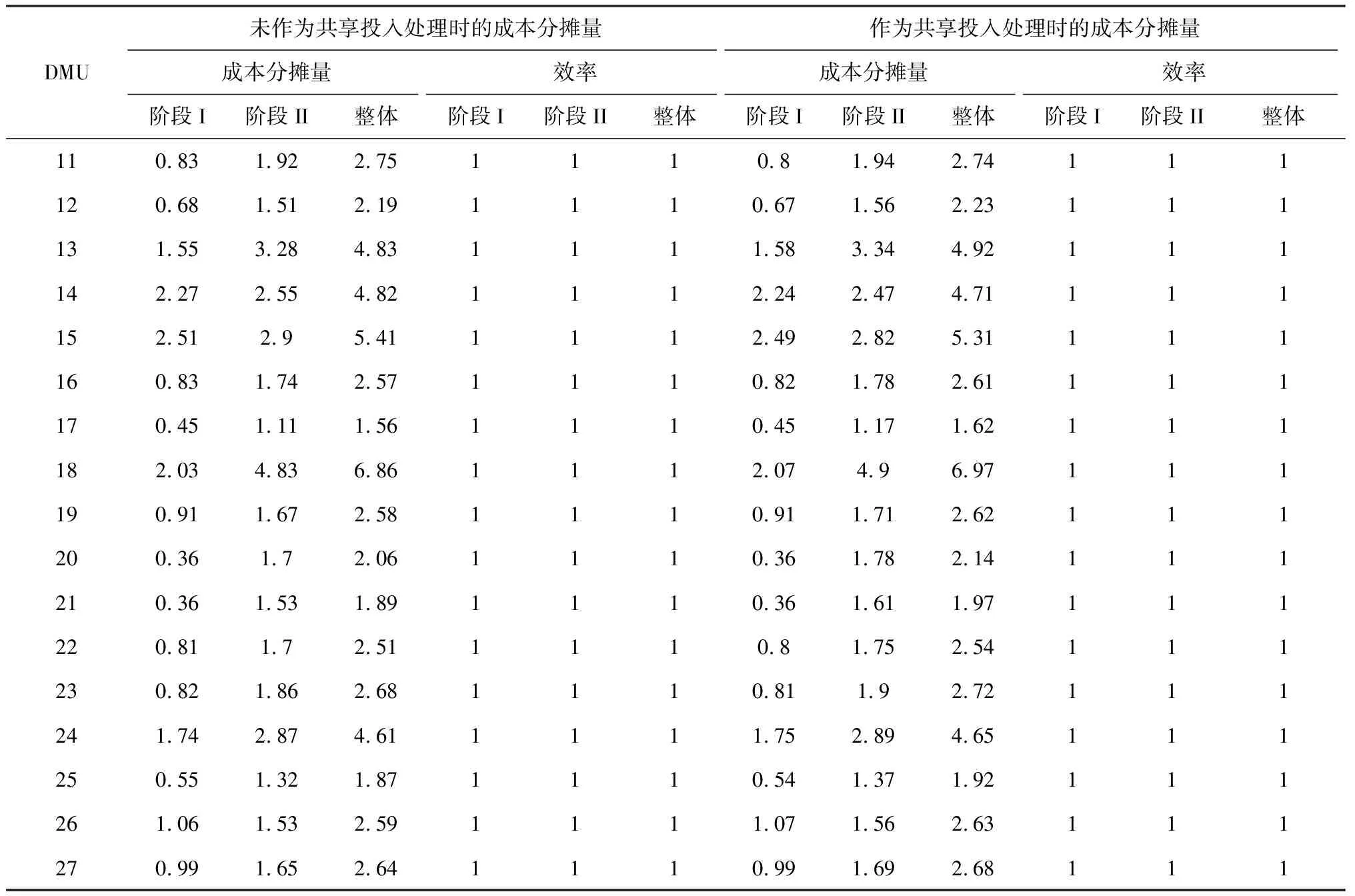
表3 是否视为共享投入的结果对比

成本分摊量都变小，阶段II的成本分摊量变大。这是因为阶段I的投入分出去一部分到阶段II，即阶段I 的投入减少，与之对应的其应该分摊的成本也随之减少。同理，阶段II的投入增加，则与之对应的其应该分摊的成本也随之增加。因此，是否考虑共享投入对成本分摊的结果是有影响的。当两阶段存在共享的投入资源时，将这些资源分配到两阶段后再进行计算更加合理。

6 结语

本文研究两阶段DEA固定成本分摊问题。首先从效率的角度出发，证明了每个DMU从自身角度出发都能够找到至少一组成本分摊方案，使得其自身达到Pareto有效。对各DMU选取相同的投入产出权重时，至少存在一种固定成本分摊方案，使得各DMU的整体和两阶段都是Pareto有效的，并给出了使得DMU的整体和阶段效率在公共的权重下都达到Pareto有效的有效成本分摊方案集。然后从公平的角度，定义了DMU各阶段对分摊方案的满意度，在满足有效成本分摊方案集的前提下，最大化最小的满意度得到最终的分摊方案。然后将问题拓展到两阶段含有共享投入的情况下，证明了这些定理和性质同样成立。数值算例部分将本文与Yu等[14]的研究结果进行了对比，验证了本文方法的可行性和有效性，指出了本文方法的优越性。

本文提出的方法适用于组织采用统一的权重进行效率评价和成本分摊的情况。例如，银行总行对各分行进行固定成本分摊、连锁超市对各子超市进行固定成本分摊、集团总公司对各子公司进行固定成本分摊等。本文既考虑了DMU的整体和阶段效率，又考虑了DMU各阶段对分摊方案的满意度，兼顾了效率和公平，得到的分摊方案合理可行，能够为管理者提供一定的决策依据。