改良技术共享下改良品联合采购联盟的竞合博弈研究
肖 旦,周永务,范丽繁,谢国杰,谢 维
(1. 广州大学工商管理学院,广东 广州 510006;2.华南理工大学工商管理学院,广东 广州 510641)
1 引言
在市场中,有一类特殊的商品,如果不考虑顾客对商品的需求,则随着时间的流逝它们的重量得到增加、数量得到增长、质量得到改善,例如,养殖场中的生猪、鸡、鸭等,鱼塘中的鱼、虾等,花圃中的鲜花,果园中的水果,酒窖中的陈年好酒等,人们称这种商品为改良品。由于某些农产品具有易损耗的特征,而本文拟讨论通过投资改良技术创新以提高改良率的改良品,因此,本文的改良品主要指以养殖户为代表的供应商所提供的产品。
近年来,越来越多的企业通过与政府部门、科研机构的合作,对改良技术进行创新,并在不同企业之间实现了改良技术的共享。例如,2017年5月,以内蒙古鄂尔多斯市达旗农牧业局的家畜改良工作站为主导,辖区内的多家农牧企业通过加大改良技术创新资金投入,加快了改良技术研发,推进了肉羊品种的改良,带动了企业的增收。而江苏省盐城市滨海县海洋林业渔业局则通过引进优质渔业品种与养殖新技术,促进全县渔业养殖企业的快速高效发展。此外,众多的养殖企业不仅共享了改良技术的创新成果,而且进行改良品的联合采购。例如,2015年,6月步步高联合生鲜采购团队在越南与芹苣,大成,雄王等当地规模最大的三个水产公司合作,成立越南巴沙鱼直采基地。
虽然,改良技术共享与联合采购可能会降低改良品采购联盟的运作成本,但是,是否选择进行改良技术创新,改良率提高到什么程度,是否进行改良技术共享,形成改良技术共享与联合采购联盟之后如何进行运作成本分摊可以保持其稳定性,是零售商进行改良技术共享后改良品联合采购联盟所需要解决的关键问题。目前,一方面已有一些学者针对改良品的采购以及改良品供应链的协调展开了积极的研究。例如,Hwang[1]首先在改良率小于(或大于)需求率的情况下,基于经典的EOQ模型构造了改良品的库存控制模型。随后,针对产品同时发生变质与改良的现象,Mondal等[2]、Moon等[3]分别考虑了改良品的需求率与价格相关、零售商的资金具有时间价值等因素影响下改良品的库存控制模型。Sana[4]在存储容量有限的情况下,研究了改良品需求受到零售商销售努力影响时进行多物品联合采购的模型。而针对改良品供应链的协调研究,国内学者王勇等[5]首先采用数量折扣作为激励机制,研究了一个供应商和一个零售商构成的改良品二级供应链在批量对批量供应模式假设下的协调问题,孙海雷等[6]则分析了如何利用价格折扣的激励方式来实现对改良品二级供应链的协作控制;张云丰等[7]采用批量对批量的供应模式,允许零售商缺货且缺货量全部拖后,比较了分散决策与集中决策下的供应链最优订购策略;张云丰等[8]考虑在单一供应商和单一零售商构成的两级改良品供应链系统中,通过设计价格折扣和交易信用作为协调机制,研究了分散式供应链下各成员企业的利润状况及协调问题。
此外,与本文相关的另一方面的研究文献为针对联合采购联盟的运作策略与稳定性分析。首先,Meca等[9-11]分别在不同的情形下,采用EOQ模型讨论了n个零售商的联合订货问题;在此基础上,Lin和Lin[12]、冯海荣等[13]讨论了多个零售商联合采购易腐品的成本分摊问题;Zhang[14]研究了多零售商共用一个中心仓库时的补货策略;Chen[15]考虑了需求依赖价格时多个零售商进行联合采购的问题;Fiestras-Janeiro等[16]研究了多个零售商可进行合作运输时的联合采购问题;肖旦等[17]在随机需求环境下分析了零售商联合采购与合并运输联盟的稳定性。而在制造商供应商可提供数量折扣契约时,肖旦和周永务[18]讨论了制造商与零售商进行库存合作时的运作策略问题;肖旦等[19]采用最大一致集的概念,研究了横向竞争零售商联合采购联盟的稳定性。而关于改良品的联合采购模型,则仅有张云丰等[20]在非瞬时补货的情形下,讨论了改良品联合采购联盟的成本分摊问题。
以上这些文献对联合采购联盟的稳定性展开了一系列的分析,但是,他们并没有考虑到联合采购联盟成员间存在竞合博弈的情景。针对此问题,在知识共享网络中,Bernstein等[21]首先对零售商间的竞合博弈策略展开了研究;随后,肖旦等[22]在随机需求下讨论了库存技术共享零售商联合采购联盟的竞合博弈策略。但是,对于零售商间先各自进行改良技术创新投资,然后共享改良技术并联合采购改良品的情形,上述文献都尚未进行研究。
本文采用逆推归纳法,针对确定的改良品市场需求,在既有改良技术投资竞争又有改良技术共享合作的情形下,分析了改良品联合采购联盟的运作策略、成本分摊规则与稳定性。本文的具体结构如下:首先,当零售商各自进行改良技术创新并在联盟内共享改良技术时,确定了改良技术共享下改良品联合采购联盟的运作策略与总成本;随后,给出了一种分配方案并证明该方案在改良技术共享下改良品联合采购合作博弈的核中;最后,得到了平均分摊总成本的方案将不能使系统的成本达到最低,但是,发现采用该合作博弈核的极点的成本分摊规则,将可以使总成本降低至系统集中化决策时的水平。
2 模型的基本描述
本文基于经典的EOQ模型,建立了改良技术共享下改良品联合采购联盟成员间既有竞争又有合作的竞合博弈模型。改良技术共享下改良品联合采购联盟中成员的决策顺序如下:第一阶段是竞争阶段。零售商各自对改良技术进行改造升级,提高产品的改良率,在此阶段零售商之间将在改良技术的投资水平上展开竞争。第二阶段为合作阶段。此阶段将分两个步骤进行,首先,联盟内成员将共享最先进的改良技术;然后,零售商进行改良品的联合采购。
图1对上述零售商两阶段的决策顺序进行直观的刻画。首先,在竞争阶段的t1时刻,零售商们各自对改良技术进行创新改造升级,提高改良率。其次,在合作阶段的t2时刻,联盟中的零售商进行改良技术共享,统一提高联盟内零售商的改良水平;在合作阶段的t3时刻,联盟中的零售商将联合采购产品并销售给终端消费者。具体如如图1所示。

图1 改良技术共享下改良品联合采购联盟中零售商的决策顺序
符号说明:
a:零售商每次订购改良品时的补货启动费用
c:零售商订购单位改良品的成本
ca:零售商改良单位改良品的成本
n:零售商的数量
N:N={1,2,...n}全体零售商的集合
Qi:零售商i(i=1,2,…n)的订货量
Di:零售商i(i=1,2,…n)面临的市场需求率
hi:零售商i(i=1,2,…n)单位时间单位产品的持有成本
Ii(t):零售商i(i=1,2,…n)在t时刻的库存水平
Ti:零售商i(i=1,2,…n)独立订货时的订货周期
TS:零售商联盟S的统一订货周期



假设:
(1)供应商对产品的补货能力无限大,瞬时到货,不允许缺货。
(2)在改良技术共享下改良品联合采购联盟中各种信息是公共知识。
(3)改良技术共享下改良品联合采购联盟S中最高的改良率为λS,λS=maxi∈S{λi}。
3 改良技术共享改良品联合采购联盟的运作策略与成本
首先,单个零售商i的库存水平在订货周期内t时刻的库存水平Ii(t),将会由于产品改良而增加,同时由于市场需求而减少。故满足微分方程:
由于Ii(Ti)=0,则易得,
因此,每次零售商i的订货批量为:
销售改良品零售商i单位时间内总成本为:
(1)
上式中的第一项为零售商i在单位时间内订购改良品的启动费用,第二项为在单位时间内改良品的总采购费用,第三项为单位时间内改良品的总持有成本和第四项为单位时间内改良品的总改良成本。

但是,如果m(1≤m≤n)个销售改良品的零售商形成改良技术共享的改良品联合采购联盟S,该联盟首先会共享最先进的改良技术,即联盟中的改良技术将会统一达到λS,其次,将会以统一的订货周期TS向同一供应商进行采购。
改良技术共享下改良品联合采购联盟成员的库存水平在一个周期内的变化规律将如图2所示。即,在0时刻,联盟中的每一个零售商将会根据自己的需求和联盟的统一采购周期向上游供应商提出采购量。随着时间的流逝,经过统一的采购周期TS之后他们产品的库存水平将变为0,并且本文假设产品可以瞬时到货,因此,将在TS时刻开始新的联合采购活动和销售周期。

图2 改良技术共享下改良品联合采购联盟中零售商的库存水平变化
与(1)式类似,可以得到改良技术共享下改良品联合采购联盟在单位时间内的总成本为:
(2)
对ACTC(TS)关于TS求二阶导数,可知,

(3)
4 改良技术共享下改良品联合采购联盟成本的分摊方案

定理1改良技术共享下改良品联合采购情景所对应的合作博弈具有次可加性的,即对于任意S,T⊆N,且S∩T=Ø,有f(S)+f(T)≥f(S∪T)。
证明:不妨假设任意的S,T⊆N,并且满足S∩T=Ø,根据(N,f)的定义以及式(3)可知,
f(S∪T)=
λS∪T=max{λS,λT},不妨设,λS≥λT,因此,λS∪T=λS,
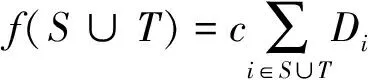
通过定理1可以知道,本文所定义的零售商在改良技术共享下改良品联合采购的合作行为将可以使所有参与合作零售商的总成本降低。此外,本文下面将通过合作博弈中核的概念,对其是否存在公平的成本分摊方案进行说明。首先,给出合作博弈核的定义如下。
定义 1:满足如下条件的集合称为合作博弈(N,f)的核:

然后,为了方便刻画公平合理成本分摊方案,本文将在改良技术共享下改良品联合采购合作博弈的基础上定义如下的合作博弈(N,v)。

下面将说明改良技术共享下改良品联合采购的合作博弈的核是非空的,即可以找到一种分配方案保持联盟的稳定性。为此本文先给出如下的定义。
定义3[22]:令π(N)是N的所有置换σ:N→N的集合,集合Pσ(i):={r∈N|σ-1(r)<σ-1(i)}含有关于置换σ的所有i的前继。

将联合采购联盟成员的产品改良率进行降序排列,并记为π(N,A),因此,本文可定义如下的成本分摊规则对改良技术共享下改良品联合采购大联盟N的总成本进行分摊:
(4)
下面的定理2将说明这种成本分摊规则对于改良技术共享下改良品联合采购联盟将是一种较为公平合理的分配方案,即该分配方案在其所对应合作博弈的核中。证明过程请参见附录。
定理2成本分摊规则P(v)=(p1(v),p2(v),…,pn(v))是改良技术共享下改良品联合采购合作博弈(N,f)的一种核分配方案。
例1:假设市场中有两个销售改良品的零售商1和2,他们不仅进行改良技术的投资竞争,而且进行技术共享和联合采购的合作。两个零售商的参数具体如表1所示,通过计算可以知道f(1)=19.79,f(2)=25.83,f({1,2})=42.72。从而,可以得到p(v)=(16.89,25.83)∈C(f)。

表1 改良品联合采购联盟中零售商的参数
5 改良技术创新时的投资博弈
本节将先讨论改良技术共享下改良品联合采购联盟中零售商在集中决策下的改良技术创新投资博弈,然后指出平均分配的方案使零售商的改良技术创新的投资决策将不会达到系统最优,最后给出了能使改良技术创新的投资达到系统最优的成本分摊方案。
首先,不妨设改良技术共享下改良品联合采购联盟对总成本的分摊方案为x(λ)=(x1(λ),…,xN(λ))∈C(f),其中,xi(λ)为进行改良技术共享与联合采购之后联盟分摊给零售商i的成本。因此,零售商i的总成本φi(λ)为:
因此,改良技术共享下改良品联合采购大联盟(即,所有零售商都参与所形成的联盟)的总成本为:
上式中第二个等式成立是因为核的定义。

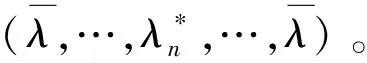
其次,下面我们将指出合作博弈阶段关于总运作成本的平均分配方案将不可能达到系统最低。


引理1. 如果给定其他零售商的改良技术创新投资,零售商i的最佳反应策略为:

证明:为了证明引理1,我们需要证明如下几个条件:
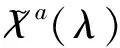

因此,可从如下几个方面展开证明:


从而上式可以得到证明。

证明:


如果在平均分配规则下,则零售商的改良率将达不到系统最优的改良率,从而导致其成本增加。

最后,与Bernstein等[21]的证明过程类似,本文指出当合作阶段选择的分配方案为改良技术共享下改良品联合采购合作博弈的核的极点时,则可以达到使改良品联合采购联盟达到系统最低的运作成本。
定理5系统集中化决策时改良技术共享下改良品联合采购联盟成员的最优竞争均衡策略,可以通过改良技术共享改良品联合采购合作博弈的核的极点得到。


从而,知道在这种分配方案下λ{1,2}=λ{1},因此,可以得到系统集中化决策时改良技术共享下改良品联合采购联盟成员的最优竞争均衡策略为(0.59, 0.1)。
6 结语
改良品是市场中一类特殊的商品,它们的品质会随着时间的流逝得以改善,越来越多的企业通过技术创新提高改良率,并形成合作联盟共享改良技术进行联合采购。但是,形成改良技术共享与联合采购联盟之后如何进行运作成本分摊可以保持其稳定性,是零售商进行改良技术共享后改良品联合采购联盟所需要解决的关键问题。本文基于经典的EOQ模型,建立了改良技术共享下改良品联合采购联盟成员间既有竞争又有合作的两阶段竞合博弈模型。首先,当零售商各自进行改良技术创新并在联盟内共享改良技术时,确定了改良技术共享下改良品联合采购联盟的运作策略与总成本;随后,给出了一种分配方案证明改良技术共享下改良品联合采购合作博弈的核是非空的;最后,指出平均分配方案所得到的改良率将低于集中化决策时零售商的最优改良率,并指出在该合作博弈核的极点的成本分摊规则下,此联合采购联盟的总成本是最低的。
本文主要讨论改良技术共享下改良品联合采购联盟的竞合博弈策略,没有考虑到随机的改良率对采购联盟运作策略的影响。总之,改良技术是否共享,改良技术共享之后运作如何分摊,将对改良品联合采购联盟的竞合博弈策略产生重要影响,这些是未来值得研究的重要问题。
附录:
定理2 成本分摊规则p(v)=(p1(v),p2(v),…,pn(v))是改良技术共享下改良品联合采购合作博弈(N,f)的一种核分配方案。
证明:
(1)与肖旦等[17]的证明过程相似,我们先考虑。
(2)含有改良率最高的零售商σ-1(1),则有,



