带工期指派的产品服务系统订单随机调度问题研究
张 杨,但 斌,高华丽
(1.重庆大学经济与工商管理学院,重庆 400044;2.重庆大学现代物流重庆市重点实验室,重庆 400030;3.西南政法大学管理学院,重庆 401120)
1 引言
随着市场竞争日益激烈和产品利润空间不断压缩,传统制造业开始由生产型制造向服务型制造转变。2016年7月,国家工信部、发改委、中国工程院联合印发了《发展服务型制造专项行动指南》[1],指出:“(制造企业)从单纯出售产品向出售‘产品+服务’转变,有利于延伸和提升价值链,提高全要素生产率、产品附加值和市场占有率”。这种“产品+服务”的整体解决方案又被称为产品服务系统(Product service system,PSS)[2]。为了按期交付产品与服务,服务型制造企业需要为客户的PSS订单制定有效的调度方案并指派合理的工期,否则就会因订单延迟交付而受到误工惩罚,甚至导致客户流失[3]。然而,在PSS的交付过程中,生产时间与服务时间可能具有随机性。例如,电梯供货与安装合同常常包含定制化需求,无法得到电梯生产与安装过程中每一道工序的精确时间,而只能结合现场操作和根据以往类似产品的生产与安装经验进行估计。这种随机性使得PSS订单调度与工期指派问题变得更为复杂。因此,在生产与服务时间均具有随机性的条件下,如何联合制定有效的PSS订单调度与工期指派策略是服务型制造企业亟待解决的现实问题。
目前,在PSS运营管理领域,尚缺乏针对PSS订单调度或工期指派问题的研究文献,而现有的PSS运营管理的定量研究主要有两类:企业宏观层面上的PSS运营策略制定和微观层面上的生产与服务任务运作计划。大多数文献从宏观角度探讨了如何制定企业的PSS运营策略,如产品和服务的定价策略、契约机制设计和能力配置等等。例如,Tsay和Agrawal[4]考虑由一个制造商和两个零售商组成的产品服务供应链,研究了零售商竞争环境下产品价格和服务水平的动态决策问题;Lee等[5]通过研究传统渠道与服务化渠道存在竞争时制造企业的最优定价与质量决策问题,发现当产品对服务的依赖性较高或渠道竞争较激烈时,制造企业实施服务化更有利;Xie Wenming等[6]在信息不对称条件下对比分析了产品服务供应链的三种契约设计,结果表明契约实施的有效性很大程度上受供应链权力结构与成本信息类型的影响;刘宇熹和谢家平[7]针对租赁PSS研究了节约共享契约对协调再制造企业与客户利益的重要作用;Xie Wenming等[8]以确保供应链中制造商和服务商间的充分信息共享为目标,探讨了如何有效规划产能和实现多渠道分销;Li Gang等[9]分析了零售商自建与外购服务能力决策对产品服务供应链成员绩效的影响,发现服务外包能够提高零售商的服务水平并降低制造商的批发价格;姚树俊和陈菊红[10]考虑由两个制造商和一个零售商组成的产品服务供应链,以制造商提供服务为视角,研究了不同权利结构下制造商的服务能力决策问题。以上文献侧重于如何通过增加企业或供应链的收益来提高利润,因此未对成本控制策略作深入探讨。仅有少数文献从企业执行层面对PSS运作过程的最优控制策略进行了研究。例如,Li Na和Jiang Zhibin[11]针对带有额外服务能力和不耐烦顾客的生产服务系统构建了分块Markov最优控制模型;Wang Kangzhou等[12]针对同时销售产品和PSS的服务型制造企业提出了最优生产与需求准入控制策略。但此类文献均假设对PSS需求按照简单的先来先服务规则进行调度,未对更为现实且有效的复杂调度策略作深入探讨和分析,而这正是本文的主要研究内容。
另一个与本文相关的研究领域是调度管理。早期,学者们主要针对生产调度[13-15]或服务调度[16-17]问题开展研究;后来,为了进一步提升MTO(make to order)型制造企业的运营效率和降低其运营成本,一些学者开始研究产品生产与配送服务的联合调度问题。例如,Garcia和Lozano[18]考虑带有时间窗的生产与配送调度问题,以最大化订单利润为目标构建了整数规划模型,并提出求解问题的禁忌搜索算法;Li等[19]针对消费类电子产品供应链研究了装配生产与空运的协同调度问题;Low等[20]以最小化最大完工时间为目标构建了时间窗约束下的生产与配送调度模型,并基于遗传算法设计了求解问题的启发式算法;马士华和吕飞[21]在随机需求条件下构建了基于Supply Hub的供应链生产与配送协同决策模型。上述研究中,产品和配送服务之间不具有严格的匹配与集成关系:同一客户订单的产品在数量较多时可由不同运输工具分批或分时段配送,同一运输工具也可以同时为多个客户提供配送服务,并且配送所需时间与选择的运输工具或运输路线相关,而非与产品本身相关。而PSS订单中的产品与服务具有高度集成性和匹配性:产品与服务往往是一一对应的关系,不同类型的产品对应的服务在服务方式和服务时间等方面不一致,且服务时间通常与产品的复杂性或客户需求相关。例如,不同型号电梯的生产与安装时间一般不同,且安装时间与客户的户型和层高等要求有关;而在电梯安装过程中,同一电梯安装队在同一时间只能为一台电梯提供安装服务。因此,以往针对生产与配送服务的调度方案不能适用于PSS订单调度问题,需要基于PSS的运作特点研究新的生产与服务集成调度策略。
鉴于此,本文考虑生产时间与服务时间的随机性影响,以最小化订单提前、误工和工期指派费用的期望总和为目标研究服务型制造企业的PSS订单调度与工期指派联合决策问题,并探讨问题的解决方案,以期为服务型制造企业的PSS订单调度管理提供有价值的启示。
2 问题描述与基本模型
2.1 问题描述与假设
考虑由一个制造工厂和n个区域服务中心组成的服务型制造企业,如图1所示。企业通过区域服务中心收集该地区客户的PSS订单需求,各订单所需产品由制造工厂集中进行生产,产品完工后运送到客户处并由相应的区域服务中心提供所需服务,从而最终完成PSS的交付。上述服务型制造企业在现实中很常见,如许多品牌电梯厂商在中国建立了电梯制造基地并在各省区设立分公司(负责该省区的电梯销售、安装和维保等业务)。在计划期的初始时刻,区域服务中心i(i=1,2,…,n)收到一个PSS订单(记为订单oi),其中订单oi由一单位产品与相应服务组成(如一台电梯的生产与安装合同)。各区域服务中心的订单构成了企业需要处理的一组确定订单集合O={o1,o2,…,on}。企业需要为每个订单指派工期并制定订单调度计划。其中订单oi的工期由两部分组成:产品工期dpi(同时也是服务交付期的开始时间)和服务交付期长度lsi(即服务交付期的截止时间dsi与产品工期dpi的差值,lsi=dsi-dpi)。例如,电梯设备生产安装合同通常会在条款中分别对电梯的交货期与安装工期进行规定。为了制定最优的订单调度与工期计划,企业需考虑在订单交付过程中可能产生的各项生产与服务费用。如果订单oi的生产在服务交付期的开始时间之前完工,产品将在库存中等待,每单位时间产生的库存费用为hi;如果订单oi的生产误工或服务延迟交付,则企业每超期一单位时间需支付给客户的误工费用为bi;此外,由于较长的工期可能会使企业丧失订单,进而损害企业的竞争力[22],故参照以往有关产品订单工期指派问题的研究[13],本文考虑订单oi每单位时间的工期时长会产生潜在的惩罚费用ai。由于各订单的收益在最初与客户谈判时就已确定,不会随订单调度计划而改变,因此为了实现利润最大化的目标,管理者需要联合决策订单序列和工期以使所有订单的期望费用总和最小。

图1 服务型制造企业运作示意图
为了方便研究,本文假设:制造工厂在同一时刻只能生产一个PSS订单的产品;各服务中心在产品到货后能够立即开始提供服务;生产时间和服务时间均是随机的和相互独立的,且服从已知正态分布;准备时间和运输时间包含在生产时间中;生产任务和服务任务一旦开始不允许中断。
2.2 基本模型
企业在决策前已知的信息包含:订单规模,各订单所需的生产时间与服务时间以及单位时间的提前、误工与工期指派费用等。据此,定义参量如下:
n:订单规模;

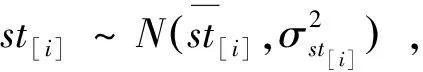
h[i]:订单[i]的单位时间提前费用;
b[i]:订单[i]的单位时间误工费用;
a[i]:订单[i]的单位时间工期指派费用;
企业直接决策的是订单序列以及产品与服务的工期,间接决策的是订单中产品与服务的完工时间。据此,定义决策变量如下:
seq:PSS订单序列;
dp[i]:订单[i]的产品工期,也是服务交付期的开始时间;
ds[i]:订单[i]的服务交付期的截止时间;
ls[i]:订单[i]的服务交付期长度,ls[i]=ds[i]-dp[i];
ctp[i]:订单[i]的产品完工时间;
cts[i]:订单[i]的服务完工时间;
其中,[i](i=1,2,…,n)表示订单序列seq中第i个位置的订单编号。此外,全文中令φ(·)和Φ(·)分别表示标准正态分布的概率密度函数和分布函数,并定义函数Ψ(x)=φ(x)-x[1-Φ(x)]。
根据问题描述和假设,给定任意PSS订单序列seq,如果该序列的第一个订单不在零时刻开始生产,或者在两个相邻的订单之间插入空闲时间,或者在同一订单的生产阶段和服务阶段之间插入空闲时间,都会推迟PSS的交付时间并产生更多工期指派费用,同时不会减少其它费用。因此问题的最优调度一定是非延迟调度,且第一个订单一定在零时刻开始生产。基于以上分析,以最小化期望总费用为目标,建立优化模型如下:
minC(seq,dp,ls)=
(1)
(2)
cts[i]=max{ctp[i],dp[i]}+st[i],i=1,2,…,n
(3)
其中,dp=(dp[1],dp[2],…,dp[n])表示产品工期向量,ls=(ls[1],ls[2],…,ls[n])表示服务交付期长度向量。式表示目标为最小化产品的期望提前费用、产品与服务的期望误工费用以及工期指派费用之和;式和分别定义了订单[i]的产品和服务的完工时间。
3 问题求解
在现实中,服务型制造企业通常先通过调度订单确定订单序列,再根据订单序列以及订单的生产时间和服务时间等信息对订单的完工时间进行估计,最后向客户承诺一个合理的工期。如果先指派工期后确定序列,由于缺少订单的排序信息,容易造成承诺的工期过短或过长。当工期过短时,由于生产时间和服务时间具有随机性,容易发生误工并产生误工成本;而工期过长可能不被客户接受甚至导致客户流失,这时企业会被迫提供价格折扣来争取订单,由此产生工期指派成本。因此,为了更好地制定工期计划和优化运营成本,企业需要先确定订单序列再指派工期。但在学术研究中,通常采用逆序求解的方法,即先假设给定任意订单序列,求得该序列下的最优工期,然后再返回决策最优订单序列。这也是求解带工期指派的调度问题常用的方法。
3.1 工期指派方法
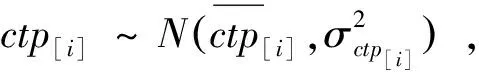
C(seq,dp,ls)
(4)
式(4)仍然比较复杂,难以直接用于问题的分析和求解。为克服这一困难,本文提出一种可以得到近似最优解的方法,该方法的主要步骤如下:
步骤1:确定原目标函数的上界和下界,并用上下界的凸组合来近似原目标函数;
步骤 2:在给定任意订单调度序列的条件下,计算近似目标函数的最优工期和最优值;
步骤3:基于近似目标函数的最优工期和最优值,设计启发式算法寻找近似最优调度解。
按照上述方法,首先推导式(4)的近似值。记V[i]Φ(θ)[Φ(κ[i](θ))-1]dθ。由积分中值定理可知,存在ξ[i]∈(y[i],z[i])使得
V[i]=Φ(ξ[i])[Φ(κ[i](ξ[i]))-1](z[i]-y[i])
又由于0<Φ(ξ[i]),Φ(κ[i](ξ[i]))<1并且z[i]>y[i],因此有
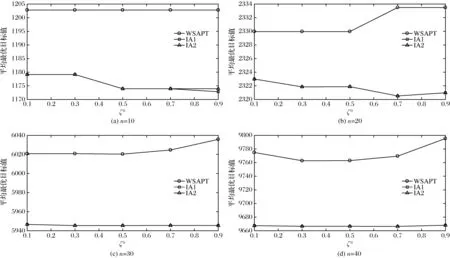
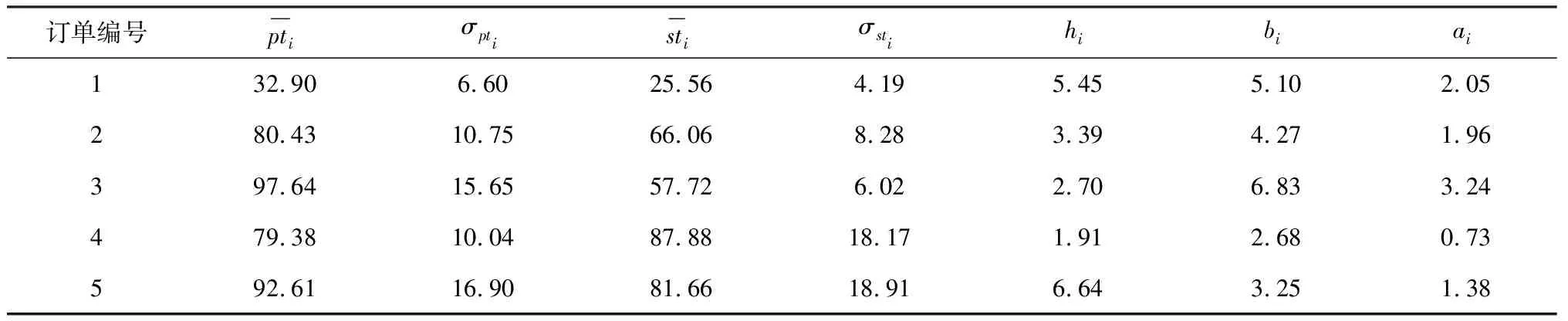
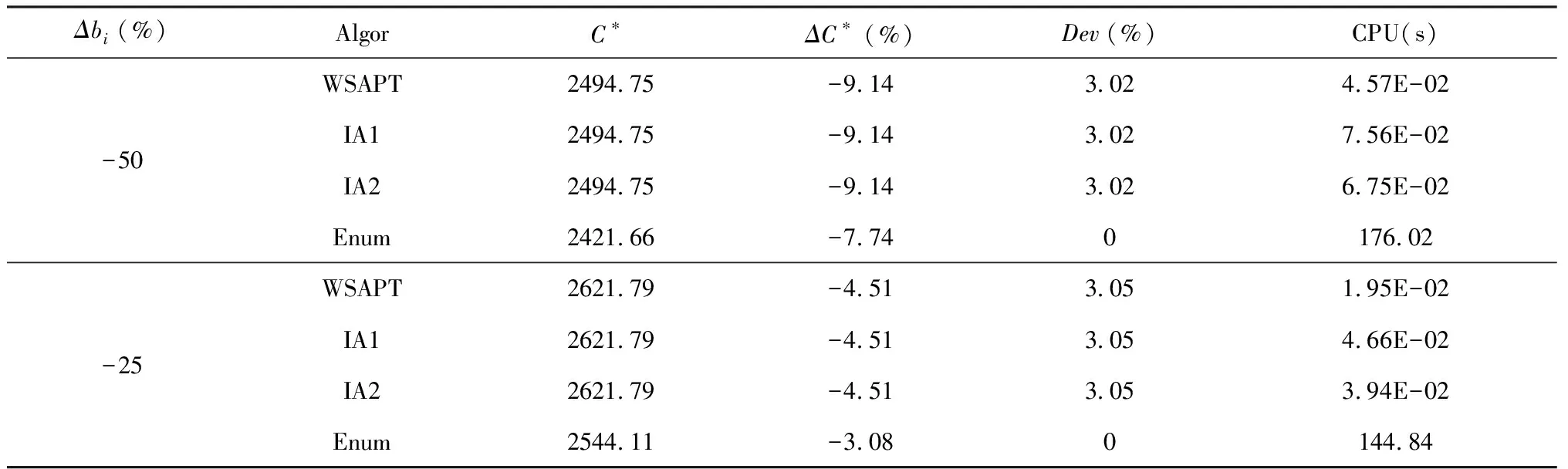
-(z[i]-y[i]) 由上式和式(4),C(seq,dp,ls)的近似值可表示为 (5) 其中τ[i]〗∈(0,1)。 定理1记 (6) (7) 联立式(6)和式(7)可得 (8) 以及 (9) 定理2记 以及 δ[i] (10) (11) (12) 证明 对任意的i,j=1,2,…,n且i≠j,由式(6)和(7)得 λ1,[i] λ2,[i] 以及 (13) 其中, φ[i] 由上式和式(12)可得 其中η[k]a[k]+δ[k]/3。下面的定理给出了能够最小化的近似最优排序规则。 定理3根据加权最短平均生产时间(weighted shortest average production time,WSAPT)排序规则: 可以得到问题 的近似最优调度解。 证明 令seq表示任意一个非WSAPT规则序列,则必存在两个相邻的订单of和og(假设分别占据seq中[]和[+1]的位置)满足 令seq′表示交换这两个订单位置得到新序列,有 以及 进而得到 上式表明交换订单of和og的位置可以得到更优的序列。证毕。 根据定理3,利用WSAPT规则对原目标函数进行优化,可得到启发式算法步骤如下: 算法WSAPT 步骤1:根据WSAPT排序规则输出调度解seq*=([1],[2],…,[n]); 步骤2:根据式(13),求解约束优化问题 其中τ(ζ)=(τ[1](ζ),τ[2](ζ),…,τ[n](ζ)); 上述算法中,步骤1可利用快速排序实现,故计算复杂度为O(nlogn);步骤2和3的目的是为求解最优序列下原目标函数的最优工期和最优值,其中问题(14)的寻优速度由具体的优化算法所决定,一般可采用已有的且比较成熟的约束优化方法,如有效集(Active-set)算法和SQP(Sequential quadratic programming)算法等等。需要说明的是,要得到序列seq*下原目标函数的最优值,步骤2实际应当执行的操作是:根据式(4),求解如下的约束优化问题: (dp*,ls*)=argminC((dp,ls|seq*) s.t.dp[i],ls[i]>0,i=1,2,…,n (15) 然而,该问题中含有2n个决策变量,当订单规模稍大时(如n≥7),问题(15)会非常耗费时间。因此,考虑在算法WSAPT中以牺牲一定的求解精度为代价,将2n维优化问题降为一维优化问题以换取时间效率。 由于WSAPT规则是基于近似目标函数上界得到的调度规则,通过WSAPT算法得到的调度解可能会与原目标函数的最优调度解存在较大偏离,因此需要引入优化机制进一步提高解的质量。本文的改进方法为:首先利用WSAPT规则产生初始解,然后对该初始解执行插入邻域局部搜索,最后选取目标值最小的解作为新的初始解。据此,提出改进的启发式算法如下: 算法IA1(inserting algorithm 1) 步骤1:根据WSAPT排序规则生成初始调度解seq0=([1],[2],…,[n]); 步骤2:令j=1并构建部分序列seqp=([j]),其中[j]是seq0中第j个位置的订单; 步骤3:将订单[j+1]插入到seqp的第k个位置,同时将该位置及后面的订单顺序后移一位,从而形成新序列seqk,其中k=1,2,…,j+1。根据式(13),计算 (16) 步骤4:令j=j+1。如果j=n,输出seq*并转步骤5;否则令seqp=seq*,转步骤3; 步骤5:根据式(13),求解约束优化问题; 算法IA1的计算复杂度为O(n3)。考虑到当订单规模较大时,算法IA1中步骤3会非常耗费时间。为了解决这一问题,可以在该步骤中对k设置一个自适应下界,使其无需试探seqp中所有可能的插入位置,就能达到与遍历所有位置相同或相近的优化效果,同时能够节省大量的运行时间。记j(n)max(1,j-「n/10⎤),其中「x⎤表示不小于x的最小整数。基于算法IA1,提出改进算法如下: 算法IA2(inserting algorithm 2) 步骤0-2,4-6与算法IA1相同,步骤3变为: 步骤3:将订单[j+1]插入到seqp的第k个位置,将该位置及后面的订单顺序后移一位,从而构成新序列seqk,其中k=j(n),j(n)+1,…,j+1。根据式(13),计算式(16)。 首先,考察三种算法的优化效果对初始化参数τi(ζ0)的敏感性。通过大量实验发现,订单规模不会对本实验的结论产生实质性的影响,因此本文仅展示四种订单规模n={10,20,30,40}的测试结果,每种订单规模包含20个随机算例。由于ζ0∈(0,1),故考虑测试ζ0={0.1,0.3,0.5,0.7,0.9}。对于每种订单规模,统计各算法在不同ζ0取值下求解20个算例的平均目标值,结果如图2所示。在图2中,算法IA1和IA2的曲线接近于重合,这是由于两种算法的优化效果十分相近。 由图2可见,各算法关于参数ζ0的单调性均是不确定的,但是各算法所得目标值的波动幅度均小于5‰,因此ζ0对三种算法优化效果的影响都很小,说明这些算法对τi初始值的扰动均具有较强的鲁棒性。正是由于这种鲁棒性,使得各算法在对ζ进行重新寻优后,无需再基于最优值ζ*调整已得到的最优订单序列。对于WSAPT算法,图2(A)表明当n=10时,ζ0的不同取值并未对算法性能产生影响;由图2(B)和2(C)可见,当n=20或n=30时,ζ0取值大于0.5会使算法性能下降;图2(D)则表明当n=40时,ζ0取值为0.3要优于其它取值。综合来看,对于WSAPT算法,ζ0的一个合适取值是0.3。对IA1和IA2算法的结果进行类似分析,可将两种算法中ζ0的值选定为0.7。 下面考察各算法的优化结果对单位时间提前费用、误工费用和工期指派费用的敏感性。通过大量实验发现,敏感性分析的实验结论适用于任意规模的算例。因此,这里仅展示一个随机产生的小规模(n=5)测试问题的相关结果,该问题的参数由表1给出。 图2 参数ζ0对各算法所得目标值的影响 针对该测试问题,分别应用各算法对单位时间的提前费用hi、误工费用bi和工期指派费用ai进行敏感性分析,得到各算法的优化结果如表2-4所示。其中,Δhi、Δbi和Δai分别表示hi、bi和ai的变动百分比;C*表示目标值;ΔC*表示目标值的变动百分比;Dev是衡量算法求解质量的指标,表示与已知最好解的相对偏离率,其计算公式可表示为 其中,Algor表示当前算法名称,C*(Algor)表示当前算法得到的目标值,Cbest表示所有参与比较的算法所获得的最好目标值;CPU表示计算时间;Enum表示基于枚举方法的精确求解算法,通过该算法一般可以得到问题的最优解。 表1 订单规模n=5的测试问题参数 表2 hi的敏感性分析及算法比较结果 续表2 hi的敏感性分析及算法比较结果 由表2可见,当提前费用hi在-50%~50%变化时,对于Enum算法,总费用C*的变动范围仅为-2.80%~2.07%;而对于本文所提的三种算法,总费用C*的变动范围也仅为-2.25%~1.69%。这说明了通过三种算法获得的PSS订单调度优化策略较少受到库存费用偏差的影响。在企业的实际运营中,通常很难精确估计库存费用,然而在此算例下提前费用偏差对总费用的影响很小,因此决策者即便难以准确估计库存费用也能采用本文算法制定出比较有效的PSS订单调度策略。 由表3可见,当误工费用bi在-50%~50%变化时,对于Enum算法,总费用C*的变动范围为-7.74%~4.24%;对于本文所提的三种算法,总费用C*的变动范围为-9.14%~9.29%。只有当总费用的构成中有比较少的延迟相关费用时,总费用才不会因误工费用的变化而产生较大波动。因此,本文提出的PSS订单调度策略能够比较有效地减少订单误工的发生。 由表4可见,工期指派费用ai在-50%~50%变化时,对于Enum算法,总费用C*的变动范围为-43.16%~41.62%;对于本文所提的三种算法,总费用C*的变动范围为-39.01%~39.49%。因此,工期指派费用偏差对于PSS订单调度费用的影响很大,决策者在估计工期指派费用时需要格外谨慎。 表3 bi的敏感性分析及算法比较结果 续表3 bi的敏感性分析及算法比较结果 表4 ai的敏感性分析及算法比较结果 此外,表2~4还对各算法求解问题的有效性进行了初步对比,可以看出: (1)WSAPT、IA1和IA2的求解速度比精确算法Enum快4个数量级,因此时间效率优势十分明显; (2)随着误工费用的增加或工期指派费用的减少,本文算法的求解质量出现了较为明显的下降,这主要是因为当误工费用与工期指派费用间的差值变大时,近似费用函数与原费用函数的偏差会逐渐加大,从而使算法的优化效果变差;其次,本文算法采用降维寻优策略也会使求解质量有所下降。 最后用一组随机产生的算例来测试本文算法的有效性。选取订单规模n={20,40,60,80,100},对于每种订单规模随机产生50个算例,从而可以得到5×50=250个算例所组成测试算例集。 对于该组问题,衡量各算法求解质量的指标为与已知最好解的相对偏离率Dev(Algor)和获得最好解的概率Pgb(Algor),后者的计算公式为: Pgb(Algor)= 由表5可得如下结论: (1)算法IA1和IA2的相对偏离率和获得相对最好解的概率均明显优于WSAPT,因此基于WSAPT规则生成初始序列,再进一步利用插入邻域局部搜索进行优化的思路是正确且有效的; 表5 不同问题规模下的实验结果 (2)IA2的求解质量非常接近IA1,同时IA2的运行时间更短,并且问题规模越大其时间效率优势越明显,故IA2的改进策略是有效的; (3)随着订单规模逐渐增大,IA1的两个求解质量指标并未显著变化,而IA2获得最好解的概率在逐渐下降,因此IA1的求解质量更稳定; (4)综合来看,当问题规模较小时,为了保证求解质量应当采用IA1算法,而当问题规模较大时适宜采用IA2算法,因为它能够兼具较高的求解质量与时间效率。 订单调度一直是企业运营管理的研究热点和难点之一,而目前对PSS订单调度问题的研究尚处于起步阶段。本文针对由一个制造工厂和多个区域服务中心组成的服务型制造企业,考虑生产与服务时间均具有随机性,构建了PSS订单调度与工期指派联合决策问题的数学模型,并设计了启发式算法对问题进行求解。通过数值仿真的分析结果可以看出,本文的模型与算法可以在较短的时间内得到较高质量的解,同时对决策过程中相关调度参数的不确定性具有一定的鲁棒性,因此能够帮助服务型制造企业的调度人员做出合理、高效的PSS订单调度安排,同时对于服务型制造企业降低运营成本和提高服务质量也具有一定的参考价值。未来的研究方向可考虑如何设计高效的智能仿生算法来求解本文提出的问题。 附录A 由公式推出公式的详细过程: E[max{dp[i]-ctp[i],0}]= (A1) 其中 (A2) 同理,订单[i]的产品的期望延误可化简为: (A3) 令r[i](t)=ds[i]-max{t,dp[i]}以及g[i](s,t)=fst[i](s)fctp[i](t),其中 (A4) (A5) 类似式(A2)和(A3)的推导过程,通过积分运算易得: (A6) (A7) 以及 (A8) 下面对式(A7)进行变换。根据链式法则,有 (A9) 应用分步积分法,由式(A9)可得: (A10) 将式(A6)-(A8)和(A10)代入式(A5),得: (A11)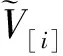




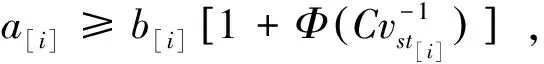



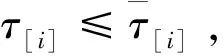
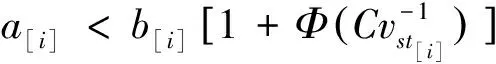


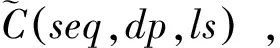

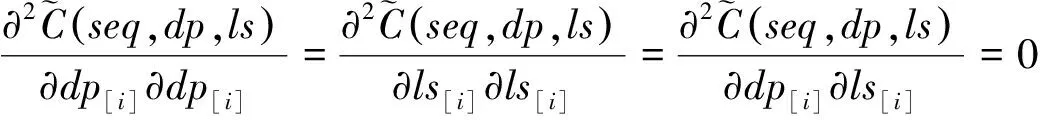

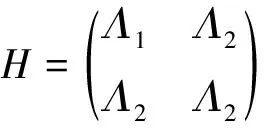

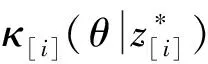
3.2 启发式算法设计

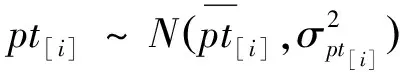



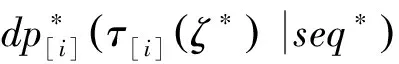


4 数值实验
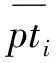




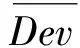

5 结语