高比例可再生能源电力系统的日前-日内两级无功功率滚动调度方法

李程昊，蒋芒，姚德贵，葛怀畅，张振安，汤磊

(1. 国网河南省电力公司电力科学研究院，郑州450052；2. 北京清大高科系统控制有限公司，北京102208)

0 引言

由于低碳环保、能源危机等因素，可再生能源发电迅猛发展[1]，电网向新能源为主体的新型电力系统转变[2]。近年来，我国风电和光伏装机持续增长，火电占比下降。2016年，冀北、甘肃等地区可再生能源装机占本地电源比例超过30%[3]。

在这样的特征下，电力系统的电压控制呈现出新的特性与挑战[4 - 5]。可再生能源具有随机性、间歇性特点，引发电压波动和电压闪变问题[6]。可再生能源发电替代常规电源，导致电网的调压能力下降，例如我国三北地区可再生能源发电以大规模集中并网为主，并网点电压支撑不足，近区成为系统薄弱环节。另一方面，可再生能源发电设备经电力电子逆变器并网，电力电子设备的异常电压耐受能力较差，电压问题引发电网安全问题，如大规模风机连锁脱网等[7 - 9]，严重影响了可再生能源可靠接入，给电力系统安全运行带来了挑战。

自动电压控制系统(automatic voltage control，AVC)可通过协调控制多类型的调压设备维持电网安全经济运行。电力系统通常配置多种类型的电压调节设备，包括慢速离散调压设备和快速连续调压设备，有不同的调节特性和响应时间常数。传统三级AVC模式[10 - 11]下，慢速调压设备仅在日内根据单一断面进行调控。典型方法为“九区图”法[12]，广泛应用于工程实践，取得了较好的电压控制效果。“九区图”法离线制定慢速设备的调节逻辑规则，在运行时根据变电站母线电压值进行慢速设备的调节决策，如电压低于某一阈值，则投电容或调节主变分接头来调高电压。对于传统电网，全天内负荷峰谷规律特征明显，电网运行方式易于预测。此外，由于可再生能源接入容量有限，系统常规电源具备足够的电压无功调节能力，因此慢速设备不会频繁动作。

然而，随着可再生能源大量并网，可再生能源的随机间歇特性使电网运行方式复杂多变，波动性增强。若仅在日内根据单一断面进行调控，不具备前瞻能力，无法考虑到不同时段间的耦合作用，慢速无功调压设备容易受到可再生能源快速随机性干扰而频繁动作。慢速设备因工作寿命限制存在全天调节次数的相关约束，日内调控可能使慢速设备因频繁动作而在一天内提前耗尽可用的调节次数，在后续时段无法保证电压控制的效果，甚至引发快慢设备间不合理的无功配置，危及电压安全。

因此，有必要在更长的时间尺度内统筹安排慢速无功调节设备，将有限的调节次数进行提前分配。可根据可再生能源短期预测结果对慢速调压设备进行日前计划，从而保证严格满足调节次数约束。文献[13]提出了针对配网的电容器计划方法，利用遗传算法和模糊聚类给出电容器投切日前计划。为应对不确定性，文献[14]优化生成风电经柔性直流汇集区域的日前电压设定值计划。文献[15]基于扩展QV节点潮流将储能功率计划作为调压手段，减少电压越限概率。文献[16]在日前得到慢速设备的动作区间计划，日内调度仅限于允许区间内动作。文献[17]考虑换流站内的调压设备动作次数限制，优化直流联络线功率。然而，可再生能源不确定性较大，短期预测误差约为15%[18]。当计划所用短期预测结果与实际运行情况偏离较大时，计划并不能保证为最优决策。在满足全天调节次数的约束下，慢速调压设备仍具备根据实际运行情况灵活调整的空间，从而提升电压控制效果。

为进一步提高电压控制效果，本文提出了“日前-日内”的两级慢速无功滚动调度方法：在日前尺度，提出了基于两阶段鲁棒优化的日前计划方法，给出各慢速离散调压设备在各小时内允许的调节次数；在日内尺度，提出了基于富余可调次数修正的日内滚动调度方法，按周期滚动进行短时间窗内的调度决策，得到慢速设备的具体调节时刻与方式，将预测误差导致的调节灵活性富余转移到后续滚动时段，从而充分挖掘慢速设备的调节能力。

本文首先介绍嵌入慢速无功滚动调度系统后AVC的整体架构，然后提出两级无功滚动调度的优化决策方法，并进行算例测试，最后对研究方法进行总结。

1 整体架构设计

1.1 “日前-日内”的两级慢速无功滚动调度原理

慢速调压设备包括容抗器组、变压器分接头等，响应速度为分钟级，因成本较低被广泛应用，但因寿命限制无法被频繁调节。若采用日前调度确定动作方式，将丧失在日内的调节灵活性；若采用日内调度，仅依靠单一断面不具备前瞻能力，引发频繁调节；若考虑多个断面，即日内调度问题考虑足够的时间窗宽，又带来较大的计算负担。

为此，本文设计了“日前-日内”慢速无功功率滚动调度系统，包括日前计划与日内滚动调度两个关键模块。日前计划根据可再生能源短期预测做出区间计划结果，但并不确定慢速调压设备的动作时刻和方式，仅将慢速调压设备的可调次数进行预分配至各个时段，从而预留一定的调节灵活性。日内滚动调度根据比相对短期预测更为精确的超短期预测进行日内滚动优化，决策出该时段内慢速设备具体的动作时刻和方式，为短时间窗内的点策略。由于日前计划的预安排，日内滚动优化考虑的时间窗较窄，有助于高效可靠地进行求解计算。变电站AVC子站将参考日内滚动调度下发的点策略，考虑内部控制逻辑，控制慢速设备，最终实现快、慢无功设备的配合。

为便于理解，本文给出一种典型日前与日内调度的时序设置方式：1)日前计划：考虑全天24 h长过程，共96点，每15 min取1个点，在每天零点启动周期，根据可再生能源短期预测结果进行优化决策，得到每小时内慢速离散调压设备允许的动作次数；2)日内滚动调度：考虑4 h长过程，共48点，每5 min取1个点，每小时周期启动，根据可再生能源超短期预测结果进行优化决策，得到该小时内慢速离散调压设备具体的调控方式。若滚动时间窗内可再生能源出力平稳，慢速设备可能不需要进行动作，因此日前计划时预留的动作次数实际上未被使用，产生了富余可调次数。可将富余可调次数叠加至下一时间窗从而增强调节灵活性。慢速无功滚动调度的时序图如图1所示。

图1 “日前-日内”两级无功滚动调度的时序图Fig.1 Sequence diagram of day-ahead and intra-day two-stage reactive power rolling dispatch

1.2 含慢速无功滚动调度系统后AVC整体框架

慢速无功滚动调度系统分为日前计划与日内滚动调度两个关键模块。该系统与AVC系统3级电压控制的协调逻辑如图2所示。图2横坐标表示每一模块的计算周期，可反映相应电压控制问题的时间尺度；纵坐标表示每一模块的层级关系，可反映控制问题的空间尺度。通过时空多尺度的协调应对高比例可再生能源电力系统的电压控制问题。日前计划与日内滚动调度用于决策慢速离散调压设备，决策优化问题中慢速离散调压设备被建模为整数变量，为整数优化。若进行全网优化，求解计算负担过重，难以保证在线应用要求，因此利用无功功率的局域特性进行分区，每一区域的AVC主站考虑各自区域情况进行独立决策。日内滚动调度最终给出小时内的调度安排下发至变电站AVC子站，变电站子站将考虑设备优先级等内部逻辑，调控子站内的电容器及电抗器(简称容抗器)、主变分接头等调压设备。另一方面，滚动调度结果也将上送至全网AVC主站进行三级电压控制。

图2 两级无功功率滚动调度与AVC 3层电压控制的协调逻辑图Fig.2 Logic diagram of coordination between two-stage reac tive power rolling dispatch and AVC three-layer voltage control

2 两级无功滚动调度模型与求解方法

2.1 基于两阶段鲁棒优化的日前计划

日前计划需提前给出慢速调压设备在每小时内的允许调节次数，同时保证满足慢速设备的调节次数约束，避免频繁调节损害工作寿命。根据短期预测信息，可在可再生能源变化幅度较大或系统调压需求较大的时段分配更多的调节次数，在变化较为平缓的时段分配较少的调节次数。

由于可再生能源短期预测的误差较大，日前决策仍面临高度不确定性，为了保证在每一可能场景下的电压控制效果，需利用不确定优化技术。鲁棒优化[19]能保证最恶劣场景下的安全性，并且不需要可再生能源的详细概率分布信息，仅需区间预测结果。此外，优化时也应充分计及慢速与快速设备间、日前与日内间的协调控制。因此，本文采用两阶段鲁棒优化方法，其中第一阶段对应日前计划决策，第二阶段对应日内滚动调度决策。

基于两阶段鲁棒优化的日前计划问题的抽象模型如下所示。

(1)

s.t.

(2)

(3)

(4)

该优化问题为多目标优化，目标为弃风量和电压离额定值的偏差最小。弃风目标权重设为远大于电压偏差目标权重，仅有电压越限时才产生弃风。

若网络约束为非线性交流潮流方程，两阶段鲁棒优化求解较难，为此采用灵敏度进行线性化，模型转换为基准点处的增量模型。系统的基准运行点可通过日前潮流预报[20]给出。式(2)根据灵敏度系数计算出系统的各状态量；式(3)为各状态变量的安全约束。

这里给出关于慢速离散调压设备的具体建模方法，日前计划可行域Y为：

(5)

(6)

式中：TNm,h为第m个有载调压变压器在第h个小时内允许的调节次数；CNn,h为第n个容抗器组在第h个小时内允许的调节次数，均为非负整数变量；TAm为第m个变压器在全天允许的调节次数；CAn为第n个容抗器组在全天允许的调节次数，TAm与CAn由调度人员设定；为自然数集合。式(5)—(6)分别表示慢速设备一天内总调节次数限制在给定上限内。

慢速离散调压设备的调节范围受日前计划TNm,h和CNn,h的影响。对有载调压变压器，将第m个变压器t时刻分接头档位记为Tm,t， 为整数变量。在第h小时的日前计划下满足约束：

(7)

(8)

(9)

同理，可对容抗器进行建模。为了降低建模的整数变量数量，对含有相同补偿容量的多个容抗器组成的容抗器组进行整体建模。将第n个容抗器组t时刻投运的容抗器数量记为Cn,t， 且为整数变量。在第h个小时内满足约束如式(10)—(12)所示。

(10)

(11)

(12)

建立的优化问题(式(1)—(3))是一个两阶段鲁棒优化，具有3层“min-max-min”结构。外层的最小化问题用以决策最恶劣场景下的最优日前计划保证鲁棒性，内层的最大化问题寻找最恶劣的可再生能源发电场景，内层的最小化问题用以模拟日内滚动调度和实时控制。两阶段鲁棒优化可采用列约束生成算法[21]迭代求解。这里给出具体的求解算法流程。原始日前计划问题(式(1)—(3))的进一步简化形式如式(13)—(16)所示。

(13)

s.t.

Ay≥d

(14)

Gx+Rz+Mu+Ey≥h

(15)

x≥0

(16)

式中：r、b分别为目标函数对应的系数向量；y和z分别为对应慢速离散调压设备的日前计划和日内滚动调度决策，为整数变量构成的向量；u为不确定性变量向量；x为经过仿射变换后的连续调压设备控制变量向量和系统状态变量向量；A、G、R、M、E为约束相应的系数矩阵；d和h为约束相应的常向量。目标式(13)中rTy表征慢速调压设备的调节次数，bTx表征网损、弃风量、动态无功裕度目标。式(14)限制了慢速调压设备一天内的调节次数；式(15)表示除式(14)外的问题所有约束。

列约束生成算法将原始问题分解为主问题和子问题求解，主问题记为MP，具体的形式为：

(17)

s.t.

Ay≥d

(18)

(19)

xl≥0,θ≥bTxl, ∀l≤L

(20)

子问题实际为给定日前计划，寻找最恶劣的可再生能源场景并上送至主问题。根据对偶定理可将子问题转换为max，由于子问题中含日内滚动对应的整数变量，需再用内层列约束生成算法求解[22]。子问题被分解为子主问题SPM和子子问题SPS。

(21)

s.t.

(22)

wkG≤b,∀k≤K

(23)

SPS：minbTx

(24)

s.t.

(25)

当主问题和子问题的目标函数值足够接近时，即相对误差小于设定的阈值，可认为算法实现收敛，求得最优解。使用该算法需多次求解混合整数线性问题(mixed-integer linear programming，MILP)，MILP问题可通过分支定界算法进行求解。总结求解算法流程如表1所示。

表1 总的求解算法流程Tab.1 Overall steps of the solution algorithm

2.2 基于富余可调次数修正的日内滚动调度

日前计划最优解对应最恶劣的可再生能源场景。然而实际场景往往并不是最恶劣场景，为了进一步提高电压控制性能，应根据超短期预测结果进行日内滚动调度，以日前计划作为边界条件，给出变压器、容抗器具体的动作方式。由于在某些时段内动作次数并未达到计划允许的上限，产生富余。因此，可将这部分灵活性调整到后续时刻。

考虑到超短期预测相对准确，且滚动调度对计算速度有更高的要求，日内滚动调度优化中的可再生能源出力使用点预测值。因此，优化问题为确定性优化。可直接使用分支定界算法求解。

日内滚动调度优化问题的抽象模型如下所示。

(26)

s.t. 式(2)—(3)

(27)

式中y*为滚动调度对应的日前计划向量。按照1.1节中的时序方式，时间窗宽为4 h，时刻点共48个，每5 min取1点。

慢速离散调压设备的约束在日内滚动层为式(7)—(12)。考虑到富余可调次数的修正，TNm,h和CNn,h还应满足如下等式约束：

(28)

(29)

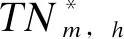
(30)

(31)

式中：TN′m,j和CN′n,h分别为根据日内滚动调度给出的有载调压变压器、容抗器在第j个小时的实际动作次数。

3 算例分析

3.1 测试系统简介

本文以某风电汇集近区电网为例构建测试系统，如图3所示。该区域共汇集最大风电容量 1 500 MW，其中风场GL和风场SJ分别装有2个4×20 Mvar的容抗器组，命名为C1和C2，一天内最多允许动作16次；KB站配有±2×1%的有载调压变压器，命名为T，一天内最多允许动作6次。

选取一天内可再生能源历史数据，根据基准值±15%得到日前预测区间。为直观验证效果，先随机采样作为实际可再生能源运行场景。如图4所示，阴影区域代表汇集区风电出力日前预测区间，虚线为预测区间中值，实线为实际运行场景。

图3 测试系统拓扑示意图Fig.3 Topology diagram of the test system

3.2 计算效率与优化结果

日前计划优化问题经过3次迭代收敛，求解时间约为10 min，在日前尺度可被接受。每1 h启动1次日内滚动调度优化，该优化问题为确定性优化不需迭代，求解时间在5 s内。

各慢速调压设备的日前计划与日内滚动调度优化结果如图5所示。由图5可见，有载调压变压器的允许动作次数在全天内分布较为均匀，容抗器组C1和C2的允许动作次数分布在前半天和后半天时段，从而使各时段预备无功调节能力。由于后半天风电变化更为剧烈，容抗器组总的允许动作次数向后半天倾斜，表明计划结果符合风电的预测趋势。以有载调压变压器T的结果为例具体阐述滚动调度结果，图5(a)圈出的时段A，在前一个小时里允许动作一次，日内滚动调度按照计划结果在期间的某一时刻进行了调节，随后几小时允许动作次数为0，日内滚动调度遵循日前计划结果未进行调节。对于时段B，尽管日前计划未分配允许动作次数，然而该时段存有1次富余动作次数，于是在后续时段根据风电波动又进行了1次调节。

图5 模拟场景下无功日前日内滚动调度优化结果Fig.5 Results of day-ahead and intra-day reactive power rolling dispatch under the simulated scenario

3.3 模拟分析结果与对比

为了说明本文提出的调度模式的优越性，与几类模式进行了对比分析。模式0：理想调控，假设已知精确的预测结果；模式1：仅日内调度，依靠单一时间断面信息日内调度慢速设备；模式2：仅日前计划，基于点预测值进行日前计划并决定慢速设备的动作方式，无日内滚动调度环节；模式3：无富余次数修正，采用本文中提出方法，但不考虑允许富余可调次数的修正；模式4：采用本文所提方法。将各个调度模式下的母线电压平均偏差值和全天弃风量做直观对比，如图6所示。为了进一步详细分析结果，图7给出了各调度模式下当天内母线电压下限值的变化情况，得到以下结论。

图6 不同调度模式优化目标对比Fig.6 Comparison of optimization objectives in different dispatch modes

图7 模拟场景下各调度模式系统母线最低电压变化情况Fig.7 Lowest bus voltage in each dispatch mode under the simulated scenarios

1)模式0，即理想调度，得到最好的调度效果，母线电压平均偏差最小，弃风量为0，然而现实中无法保证100%精度的日前可再生能源预测，其结果用于验证调度性能。

2)模式1，未利用预测信息，存在短视性，在图8所示的时段B之前已耗尽变压器可调节的次数导致后续无法调节。而时段B恰好为风电大发阶段，因各慢速调压设备无法动作导致电压越安全下限0.96 p.u.，为保证安全共弃风(折合电量)42.5 MWh。

3)模式2，由于计划结果基于点预测值，缺乏鲁棒性的考虑，在实际出力偏差预测值过多的情况下，如时段B风电大发，计划结果并不合理，慢速调压设备的无功支撑不足，导致此时电压接近下限0.96 p.u.，虽然没有弃风，但电压偏差已较大。

4)模式3和4，采用了日前计划日内滚动调度的模式，结果和理想调度接近，变压器满足可调次数约束的同时能够灵活响应实际风电出力的情况。

5)模式4和模式3相比，电压控制性能进一步提高。原本日前计划结果在某些时段不允许慢速调压设备动作，例如在时段C有载调压器不允许动作。然而调度模式4下，实际运行发现还有富余动作次数，因此修正后的日内滚动调度在后续时刻调节了变压器使得系统母线电压得到提升。由图7可知，时段A和时段C中模式4相比模式3电压水平更高；综合看全天平均电压偏差，模式4也小于模式3。将该天内的慢速调压设备动作次数进行统计：模式0下，慢速调压设备分别动作16、14、6次；模式3下，分别动作10、8、4次；模式4下，分别动作16、14、6次，与理想调度一致。因此，本文所提调度模式充分发挥了调节灵活性。

采用蒙特卡洛仿真进行对比。在日前风电预测区间内随机生成10 000个风电场景，模拟各调度模式的运行结果，如表2所示。从平均电压控制效果来看所提调度模式最为接近于理想调度。模式1电压平均偏差最大，且存在弃风场景；模式2电压平均偏差稍好，由于未考虑不确定性，同样存在弃风场景；模式3采用日前计划和日内滚动调度模式，由于采取了鲁棒优化，所有场景均未弃风，然而未考虑次数修正，电压平均偏差不是最优。

表2 蒙特卡洛仿真结果Tab.2 Monte Carlo simulation results

3.4 大规模系统测试结果

为了进一步验证所提方法的有效性和可扩展性，本文基于含高比例可再生能源的IEEE 118节点标准算例[23]开展了测试，该系统包含17个风电场，容量均为150 MVA。在部分负荷母线和近区线路配置了10个4×20 Mvar的容抗器组和4个±2×1%的有载调压变压器。对于该系统，日前计划问题求解时间约为1 h，日内调度求解时间约为20 s。

本文对比了日前计划采取场景优化方法和确定性优化方法。其中场景优化方法指使用K-means聚类算法得到10个典型风电场景进行优化，确定性优化方法指基于风电输出期望值进行优化。3类方法可得到不同的日前计划结果，再随机生成10 000个风电场景进行日内滚动调度，模拟各方法下的运行结果，如表3所示。鲁棒优化方法由于考虑了最恶劣场景，最大弃风量和电压平均偏差都最优；场景法考虑了风电的不确定性，电压平均偏差与鲁棒法接近，但在恶劣场景下的弃风量会更大，因为场景采样难以计及极端恶劣场景；确定法未考虑不确定性，因此电压偏差和最大弃风量都较大。

表3 IEEE 118系统蒙特卡洛仿真结果Tab.3 Monte Carlo simulation results of the IEEE 118 system

3.5 线性化误差

为了使鲁棒优化可高效求解，优化问题建立了基于灵敏度的线性化模型。这里将优化问题中的电压幅值与精确交流潮流模型下的电压幅值进行对比。计算出10 000个场景下节点电压幅值的均方根误差如图8所示。可以看到最大均方根误差对应风电大发时刻，但仍然在1.5×10-3以内。由于优化解位于基准点的领域内，灵敏度线性潮流近似效果较精确，优化得到的结果可以接受。

图8 灵敏度计算电压幅值均方根误差Fig.8 Root mean square errors of voltage magnitudes under the sensitivity calculation method

3.6 计算效率

日前计划与日内滚动调度对于大规模系统可能存在计算效率低的问题。尤其对于日内滚动调度，系统需及时地给出调度策略。可采取电压分区[24 - 25]的方式，对每一个较小的区域进行无功功率滚动调度，从而降低问题的计算规模。在参数的设置中，可以调整主问题子问题目标值的相对误差阈值、MILP容忍间隙、最大迭代次数等，以牺牲最优性的代价来保证计算效率。此外，在求解算法流程中，可以通过启发式等策略[26]缩减场景减少迭代次数。

4 结语

随着高比例可再生能源的大规模并网，快慢调压设备需要在多个时间尺度协调安排，统筹兼顾，共同支撑可再生能源可靠并网，保证电网电压安全。本文针对高比例可再生能源电力系统的慢速离散调压设备调度问题，提出了慢速无功日前—日内两级无功滚动调度方法。测试效果表明本系统在可再生能源的高不确定性下可合理安排慢速调压设备，提高电压安全裕度，增强电压支撑能力。采用日前计划与日内滚动调度相比其余优化调度方法的电压控制性能更为优越，通过富余可调次数的修正进一步提高慢速设备的灵活性，增强电压控制性能。