基于自适应噪声完备集合经验模态分解与独立分量分析的故障选线法

杜磊，徐天奇，李琰，朱梦梦，何兆磊

(1.云南省高校电力信息物理融合系统重点实验室，昆明650504；2. 云南省高校信息与通信安全灾备重点实验室(云南民族大学)，昆明650504； 3. 云南电网有限责任公司电力科学研究院，昆明650217；4. 云南电网有限责任公司计量中心，昆明650000)

0 引言

我国配电网大多采用经消弧线圈接地的方式，有利于提高供电可靠性，在发生单相接地故障后需要在继续维持运行的1～2 h内排除故障线路，否则不仅可能损坏设备绝缘，还可能扩大故障范围。如果在故障发生后开断故障线路前，该母线上的其他线路又发生单相接地故障，现有的方法无法有效识别故障线路。

目前的故障线路识别选择方法较多，包括基于时频分析方法的暂态能量法[1 - 6]、注入法[7 - 8]、功率法[9 - 10]、导纳法[11 - 12]、相关分析法[13 - 14]、频域参数识别法[15]、聚类分析法[16]、神经网络及融合原理法[17 - 18]等。由于线路零序电流发生畸变、故障电流相位发生变化等情况都会对选线产生一定的影响。文献[2]利用短窗数据做S变换，但如果故障线路上存在较大的感性负载，使得故障发生后首半波零序电流严重畸变，严重影响选线正确率。文献[3]利用5 ms的暂态零序电流数据做小波变换后进行相关性分析，由于电缆线路容抗大于架空线路容抗，故障线路零序电流相位改变，所以造成故障线路与健全线路的零序电流波形相似度增加，采用相关性分析虽然计算速度快，但对于情况多变的馈线，实际应用时正确率会下降。文献[18]使用BP神经网络进行故障选线，需要收集大量的数据进行训练，目前还没有完备的数据库支持训练出适合普遍配电网的模型，可信度暂时不能得到保证，所以在实际选线过程中没有用人工智能的方法来实现选线。

已有大量学者在故障选线方面开展了丰富的研究极。但选线正确率受到零序电流波形畸变程度以及故障线路与健全线路零序电流区别度的影响，对于发生概率极小的相继故障情况，现有的故障选线方法通常在查出第一条故障线路并开断该线路后才判断零序电流是否仍然存在，若存在则再次启动判据判断出所有的故障线路[5]。本文选线原理根据故障线路零序电流由工频交流分量、暂态高频振荡分量和衰减直流分量3部分叠加而成；若发生单相接地故障就会产生故障分量，若线路存在故障分量就可以判断为故障线路；所以该方法不仅可以解决零序电流波形畸变及相似性增加带来的影响，同时也不受相继故障及高阻故障的影响。

综上所述，本文提出了一种基于自适应噪声完备集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)和独立分量分析(independent component analysis，ICA)的故障选线方法，将多维源信号压缩后提取独立成分分量，然后利用峭度阈值判据判别独立成分分量中暂态高频振荡故障信号、工频交流信号和衰减直流信号并重构线路零序电流信号；判别重构线路零序电流信号方差为零的线路为故障选线。仿真结果表明所提方法选线可靠性高，适用性广。

1 选线原理

1.1 CEEMDAN 算法

自适应噪声完备集合经验模态分解(complete ensemble empirical mode decomposition based on adaptive noise，CEEMDAN)是在集合经验模态分解(empirical mode decomposition，EEMD)的基础上改进的，CEEMDAN在每一阶段添加自适应高斯白噪声，能有效解决EMD模态混叠现象同时克服EEMD分解效率低和噪声难以完全消除的问题[19 - 24]。使用CEEMDAN可以有效提取每一条线路的各种特征。

定义Ek(·)表示EMD分解得到的第k个模态，FIMFk为CEEMDAN的第k个模态分量，其具体分解步骤如下。

1)将各线路首端零序电流信号x加入m组高斯白噪声合成带有噪声的零序电流信号xi，即：

xi=x+βkwi

(1)

式中：wi(i=1,2,…,m)为1组单位方差均值为0的高斯白噪声；βk为所添加高斯白噪声的标准差。

2)通过EMD计算获得第1个模态。

(2)

则一级残差为：

r1=x-FIMF1

(3)

3)计算第2个残差和第2个模态。

(4)

r2=r1-FIMF2

(5)

4)依次类推计算第k个残差和第k个模态。

(6)

rk=rk-1-FIMFk

(7)

5)重复步骤4)直至残差不能被分解，计算得到全部IMF。

故障线路首端的暂态零序电流为：

(8)

式中：IC、IL分别为电容电流ic和电感电流iL的幅值；ωf为暂态自由振荡分量的角频率；ω为工频；φ为零序电压的初始相位；t为时间；τL、τC分别为电感回路与电容回路的时间常数。

故障零序电流由稳态工频交流分量、暂态高频振荡分量和衰减直流分量3部分叠加而成[25]。故障线路首端由电容和电感提供暂态零序电流，而健全线路只由电容提供暂态零序电流。由此可得到故障线路零序电流与健全线路零序电流的根本区别；识别故障线路首先将3个分量提取出来；本文采用自适应噪声完备集合经验模态分解，不仅解决了EMD模态混叠问题，同时相比于EEMD，加入了自适应高斯白噪声并增加迭代次数，既解决了不同信号在噪声影响下的模式数，又减小了分解误差。在CEEMDAN分解后按照贡献率从高到低依次排列，可将各线路零序电流贡献率最高的工频交流分量、暂态高频振荡分量和衰减直流分量3部分提取。

1.2 独立分量分析

独立分量分析法(independent components analysis，ICA)常用于盲源分离。可将多个信号S在多个传输通道A合成的多个信号X分离开来，如图1所示。图中：

信号源S：S(t)={s1(t),s2(t),…,sn(t)}

(9)

A为混合矩阵，表示各传输通道对各信号源的传输能力；

观测信号X：X(t)={x1(t),x2(t),…,xn(t)}

(10)

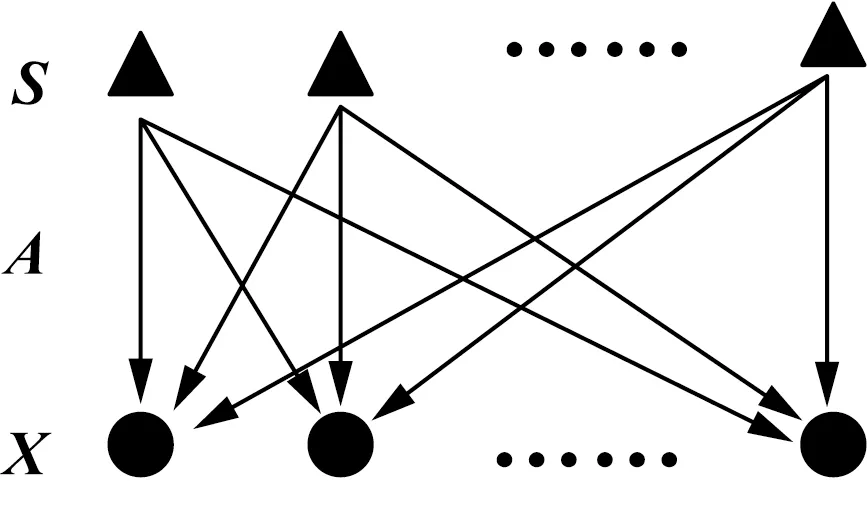
图1 独立分量分析法Fig.1 Independent component analysis

可得到X=AS, 在S和A未知的情况下可通过求解混合矩阵W从X中分离出S的估计Y，即Y=WX=WAS, 但S必须都相互独立且不为高斯分布；通过ICA分离出来的S无法计算其能量及S的方向。分离ICA的主要步骤如下：

1)数据中心化，剔除平均值；

2)白化过程去除数据的沉余信息；

3)正交化处理；

4)缩放变量，使其方差=1；

5)使用优化算法使每个信号最大限度的非高斯性。

总体来说，独立分量分析=白化+高斯性。通过ICA分离处理的S可通过逆变换恢复X。

主成分分析(principal components analysis，PCA)用于分析信号间的非相关性[17]，可以垂向降维；ICA则用于分析信号间彼此独立性。PCA的降维提取信号是ICA的预处理步骤。由于线路零序电流由3部分组成，所以将经过CEEMDAN分解后按照贡献率从高到低依次排列的IMF分量垂向降维到贡献率前三的IMF分量，不仅可以减小逆变换后的重构误差，同时也大大减小了ICA的计算量。根据分析，故障线路由1个主元素构成；健全线路由2个主元素构成；使用ICA逐个投影追踪估计出2个独立成分分量用于故障选线。由于3个分量对故障线路和健全路线贡献率不同，可知估计出的2个独立成分分量也不同。工频交流分量和衰减直流分量对故障线路贡献率大，在估计独立成分分量时暂态高频振荡分量就被过滤掉。暂态高频振荡分量对健全线路贡献大，在估计2个独立成分分量时，暂态高频振荡分量必在其中。使用ICA估计独立分量时由于数据中心化及缩放变量使得E{Si2}=1， 估计出的独立分量不能确定其能量及方向。因为S相互独立可通过逆变换将估计出的独立分量还原为原始线路首端零序电流。

1.3 峭度

峭度因子可用来反映冲击特性对暂态高频振荡分量具有较高的敏感度。可以用峭度准则判断是否存在工频交流分量和衰减直流分量[26 - 27]。从而选择出故障线路。

峭度K的公式为：

(11)

式中：E(x)为变量x的期望值；x为各线路ICA分解后的信号；μ为信号均值；δ为信号标准差。

通过ICA估计出的独立分量不能确定方向即独立分量乘以-1并不影响方差，为准确选出故障线路且不受方向影响，本文提出使用关于期望与标准差四次幂的峭度函数选线。

图2 故障零序电流理想等效分量Fig.2 Ideal equivalent component of fault zero sequence current

由图2可知y1为工频交流分量，其峭度值K=1.499 6。y2为暂态高频振荡分量，其峭度K=603.266 4。y3为衰减直流分量，其峭度值K=1.800 8。重构故障信号时暂态高频振荡分量的峭度值K与另外两个分量有很明显的区别。

经独立分量分析估计出的两个独立成分分量用峭度阈值判断是否属于暂态高频振荡分量，将对故障线路贡献率大的工频交流分量和衰减直流分量置零后，故障线路将不存在独立成分分量；而所有的健全线路必然剩下暂态高频振荡分量。在进行独立分量逆变换后故障线路电流被置0，健全线路为剩下的独立分量的逆变化。由此可得到线路的重构零序电流信号；可以精确确定故障线路，无需使用最大值原理确定故障线路。为方便观察出故障线路，计算各馈线重构零序电流信号的方差，方差为0的即为故障线路，不为0的即为健全线路，全部不为0的为母线故障。

为减少试拉闸处理及重新排定相继故障时的拉闸顺序，本文提出根据峭度值大小，从小到大的“排序推拉”策略。在选线过程中得到两个独立成分分量的峭度值，将两峭度值相加后进行排序，其数值越小则其为故障路线的可能性越大。试拉闸处理中按峭度值从小到大的“排序推拉”可提高故障选线的准确率。

对于故障特征小的高阻接地故障，故障线路零序电流工频交流分量和衰减直流分量贡献率降低；易与母线故障特征相似，为使暂态高频振荡分量冲击特性提高和根据峭度值大小的“排序推拉”策略特征加强，同时为防止馈线高阻接地故障被误判为极其严重的母线故障，减少停电面积和停电经济损失；为高阻接地故障和母线故障补上故障前45 °的零序电流数据(故障前零序电压为0，零序电流也为0)；工频交流分量、暂态高频振荡分量和衰减直流分量峭度值都增加，但暂态高频振荡分量增加量极大；使得母线故障时各馈线特征增大且趋势相同与馈线接地故障区分，同时故障线路故障特征比健全线路更明显，易确定故障线路。

2 单相接地故障选线步骤

本文所提选线方法如图3所示，主要步骤如下。

1)确认系统发生单相接地故障后，采集4个工频周期内各馈线首端零序电流。采样频率10 kHz。

2)对各馈线首端零序电流进行自适应噪声完备集合经验模态分解，分别得到各馈线的IMF。

3)将各馈线的IMF降维到3维后估计出2个独立成分分量。

4)使用峭度准则对各馈线的两个独立成分分量进行计算并将峭度小于20的独立成分置0。

5)将各馈线的独立成分分量进行逆变换并叠加，重构各馈线信号，此时故障线路重构零序电流已被置0，健全线路重构零序电流都不为0(对故障线路零序电流贡献率大的工频交流分量和衰减直流分量全部置0，对健全线路贡献率大的暂态高频振荡分量保留)。

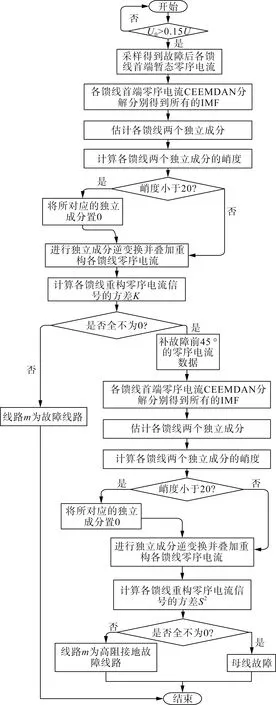
图3 故障选线流程图Fig.3 Flowchart of fault line selection

6)计算各馈线重构的零序电流方差S2，方差S2为0的线路为故障线路，若方差S2全不为0则补上故障前45 °的零序电流重复步骤2至5，方差S2为0的线路就是高阻接地故障线路；全不为0则为母线故障。

3 仿真验证

3.1 仿真模型

利用PSCAD软件搭建配网谐振接地系统仿真模型[28]，如图4所示。消弧线圈电感值为0.296 H，由图5可得故障线路由1个主元素构成；健全线路由2个主元素构成；结合故障线路零序电流可分解为工频交流分量、高频振荡分量和衰减直流分量3部分叠加而成。所以将各馈线的IMF分量降到3维后估计出2个独立成分分量，如图6所示。

等值电阻为2.793 9 Ω，过补偿度为8%。采样频率为10 000 Hz。负载每相有功功率为1 MW，功率因素为0.89。线路参数见表1。其中R、L、C分别为线路电阻、电感和对地电容的值；下标1、0分别代表正序、零序参数。

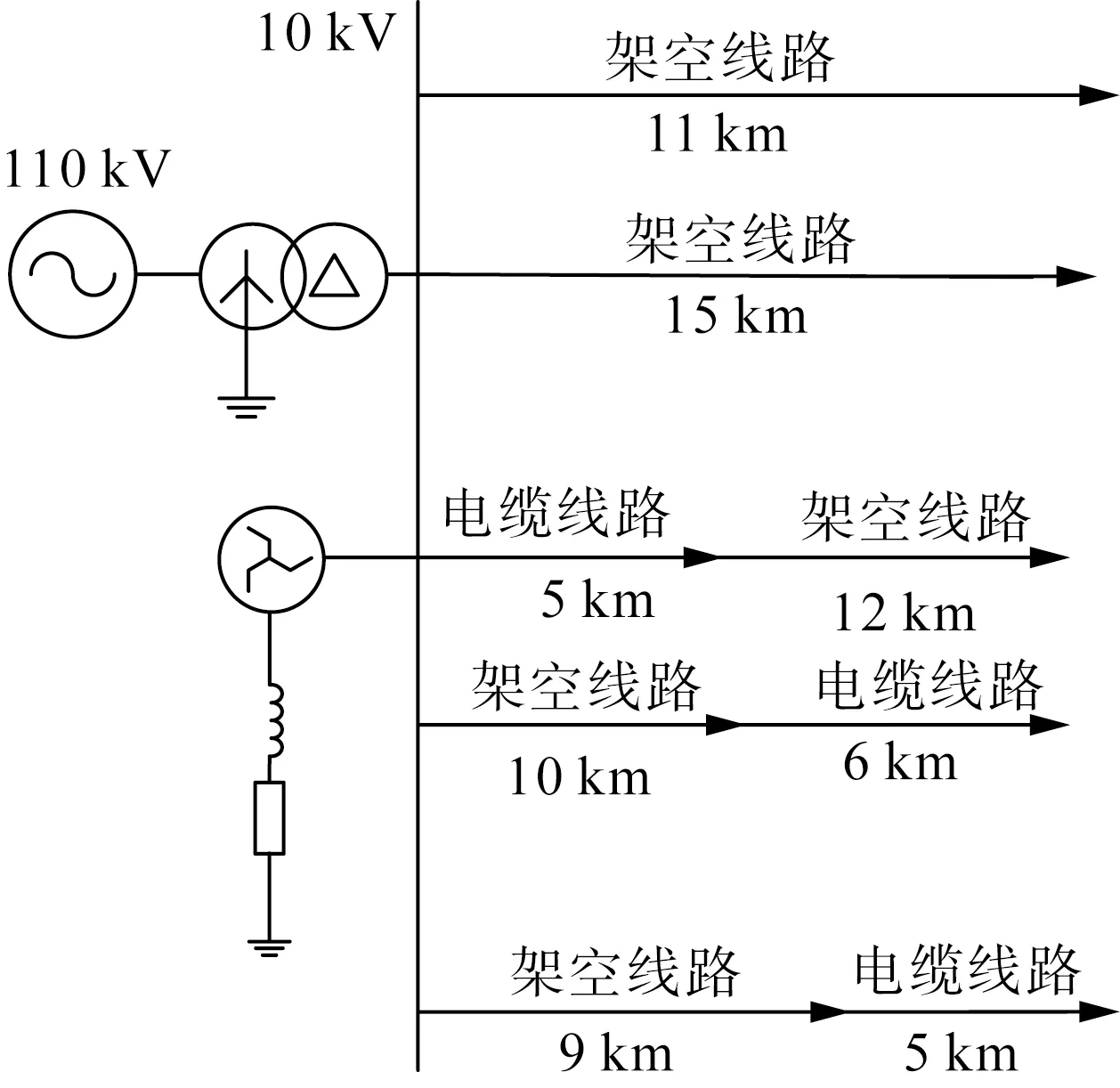
图4 谐振接地系统模型Fig.4 Resonant grounding system model

图5 馈线1-5各IMF分量的贡献率Fig.5 Contribution rate of each IMF component of feeder 1-5

图6 各馈线的两个独立成分分量Fig.6 Two independent components of each feeder

表1 线路参数表Tab.1 Line parameter table

3.2 算例分析

将线路按照由上至下的顺序编号。

本文算例分析分为4种典型接地故障：故障1为架空线路接地故障；故障2为缆-线混合高阻接地故障；故障3为母线故障；故障4为馈线相继接地故障。

故障1：线路2在距离母线6 km 处发生故障，接地过渡电阻为500 Ω，合闸角为90 °。采集所有馈线的首端零序电流。将各馈线的首端零序电流分别做CEEMDAN分解；噪声标准偏差设置为0.2 dB；实现数为100；允许的最大筛选迭代次数为20次。得出各馈线的所有IMF分量。对各馈线CEEMDAN分解后的各分量进行独立成分分析，可得各分量的贡献率如图5所示。

由图6可知故障线路主要由工频交流分量和衰减直流分量2个独立成分分量组成，健全线路中高频振荡分量占主要成份，由此需要一个能够把暂态分量提取出来的算法，本文采用的是峭度，可以判断波形的平缓程度，由于暂态高频振荡信号的峭度值比工频交流信号和衰减直流信号的峭度值大，可将暂态高频振荡信号有效选取。由于ICA不能计算能量和方向，线路1独立分量2波型反向；由于峭度是关于期望与标准差4次幂的函数所以不影响峭度对波型平稳的计算。各独立成分分量的峭度值见表2。将工频交流分量与衰减直流分量置0。

表2 各独立成分分量的峭度值Tab.2 Kurtosis values of each independent component

将各馈线的独立成分分量进行独立成分的逆变换并叠加重构各馈线零序电流信号如图7所示。

图7 各馈线的CEEMDAN-ICA重构首端暂态零序电流与原始首端暂态零序电流Fig.7 The CEEMDAN-ICA of each feeder is used to reconstruct the transient zero-sequence current at the head end and the original transient zero-sequence current at the head end

计算各馈线重构的零序电流方差S2，S2等于0即为故障线路，S2全不为0则为母线故障。

表3 各重构零序电流的方差值Tab.3 Variance values of each reconstructed zero sequence current

因此判定线路2故障与假设一致，选线正确。

故障2：线路4在距离母线3 km处发生故障，接地过渡电阻为20 kΩ，合闸角为45 °。采集馈线的首端零序电流。实验数据如表4—5和图8所示。

表4 各独立成分分量的峭度值Tab.4 Kurtosis values of each independent component

表5 各重构零序电流的方差值Tab.5 Variance values of each recovery zero-sequence current

图8 各馈线的CEEMDAN-ICA重构首端暂态零序电流与原始首端暂态零序电流Fig.8 Reconstructed transient zero-sequence current at the head end by CEEMDAN-ICA of each feeder and the original transient zero-sequence current at the head end

因此判定线路4故障，与假设一致，选线正确。该方法对于高阻抗接地故障及全补偿情况仍然适用。对于接有电缆的线路虽然零序电流有所滞后、暂态量明显减少，但本文的方法仍不受影响，故障线路的主要独立成分分量仍然估计为工频交流分量；健全线路的主要独立成分分量估计为高频振荡分量和衰减直流分量；与架空线的输电线路独立成分估计一致；可用于缆-线混合线路。

故障3：母线发生故障，过渡电阻为1 000 Ω，合闸角为0 °。实验数据如表6—7、图9—11所示。由表7可判定线路为母线故障，与假设一致，选线正确。由图9可知母线故障时各馈线相似度很高，与全补偿情况下线路故障很难区分；由图10可知对于本文方法，母线故障时各馈线高频振荡分量为主要独立分量，所以各馈线的峭度值都很大很容易判断出母线故障。在重构故障信号时各馈线信号都未被全部置零；其方差全部不为零。对于缆-线混合线路，由于电缆使得线路中容抗增加，衰减直流分量减少，工频交流分量增加；其主要独立成分峭度值比架空线路略小。故障4：线路1距离母线3 km 处发生故障，过渡电阻为500 Ω，合闸角为45°。线路5距离母线9 km 处发生故障，过渡电阻为50 Ω，合闸角为90 °。采集所有馈线的首端零序电流，如图12所示。各馈线独立成分分量如图13所示。各馈线的CEEMDAN-ICA重构首端暂态零序电流与原始首端暂态零序电流，如图14所示。各独立成分分量的峭度值如表8所示。各重构零序电流的方差值如表9所示。

表6 各独立成分分量的峭度值Tab.6 kurtosis values of each independent component

表7 各重构零序电流的方差值Tab.7 Variance value of each reconstructed zero sequence current current

图9 各馈线首端零序电流Fig.9 Zero-sequence current at the head end of each feeder

图10 各馈线的两个独立成分分量Fig.10 Two independent components of each feeder

图11 各馈线的CEEMDAN-ICA重构首端暂态零序电流与原始首端暂态零序电流Fig.11 Reconstructed transient zero-sequence current at the head end by CEEMDAN-ICA of each feeder and original transient zero-sequence current at the head end

由图12可知在相继故障时线路1首先发生单线接地故障，线路1故障瞬间零序电流为负，其他线路故障瞬间零序电流为正，故障线路与健全线路反向；对于健全线路在第一次故障后暂态分量很快消失；线路5发生第二次单相接地瞬间故障，线路5零序电流为正，其他线路零序电流为负，同时线路5的零序电流急剧增加，由于故障线路5的接地电阻比线路1的接地电阻小，所以线路5的零序电流比线路1的大。

图12 各馈线首端零序电流Fig.12 Zero-sequence current at the head end of each feeder

由图13可知故障线路的第一个独立成分分量都为工频交流分量；健全线路的第一个独立成分分量都由两个暂态高频振荡分量组成，峭度值都很大。故障线路的第二个独立成分分量为衰减直流分量，故障线路1由于线路5发生第二次故障，所以有明显突变；由于独立成分析缩放变量，使其方差等于1，不能分析方向和能量，所以故障线路5的衰减直流分量显示为反向；其峭度值都比较小，所以在重构零序电流信号时被消除。经实验验证本方法可准确判断相继故障。

图13 各馈线的两个独立成分分量Fig.13 Two independent components of each feeder

3.3 普适度分析

由于配电网现场环境复杂，故障情况多变，且不可避免地受到噪声的影响，仿真通过加入信噪比为50 dB的高斯白噪声，来测试本方法在不同故障距离X、接地过渡电阻Rf、 故障合闸角α等故障下选线的准确性。仿真结果如表10—12所示。

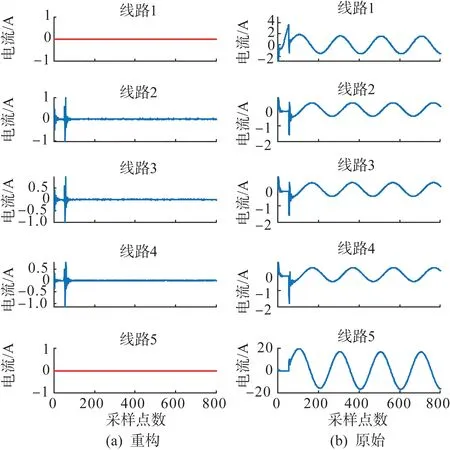
图14 各馈线的CEEMDAN-ICA重构首端暂态零序电流与原始首端暂态零序电流Fig.14 Reconstructed transient zero-sequence current at the head end by CEEMDAN-ICA of each feeder and the original transient zero-sequence current at the head end

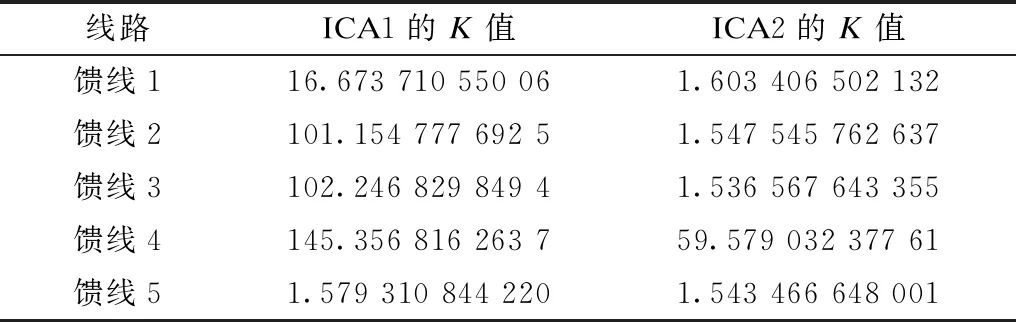
表8 各独立成分分量的峭度值Tab.8 kurtosis values of each independent component

表9 各重构零序电流的方差值Tab.9 Variance values of each reconstructed zero sequence current

本方法对于单相接地故障在各种情况下的故障都能识别。对于加入噪声后的零序电流，在CEEMDAN将噪声分离后再通过独立成分分析提取非高斯性信号，有滤除噪声的效果；高斯白噪声对本方法影响极小，50 dB的高斯白噪声峭度值位于2.514 6～3.847 7；20 dB 的高斯白噪声峭度值位于2.532 4～3.644 9；均远小于暂态高频振荡分量的峭度值。本文方法充分利用了各馈线首端零序电流的故障信息，具有良好的自适应性，对不同接地故障具有一定的鲁棒性。

表10 故障选线结果Tab.10 Result of fault line selection

表11 多路相继故障选线结果Tab.11 Result of Multiple Successive Failure Line Selection

对于相继接地故障，目前常采用“随拉随合”、“全拉试合”、“排序推拉”几种推拉策略方法解决。使用得最多的为“排序推拉”法，参考零序电流大小和经验对各馈线排除。对于全补偿多缆-线混合线路情况下的单相接地故障，根据零序电流大小排序推拉的方法会出现误判；根据经验排序推拉，用试错法排除故障线路，不仅费时费力，成本也较高。本文提出了一种根据峭度值大小的“排序推拉”策略，可根据峭度值的大小，从小到大即独立成分按波形从平稳到陡峭，按顺序推拉故障线路看零序电压是否消失来判断相继接地故障是否排除。

对于高阻接地故障，故障特征小，选线十分困难，而接地故障多为高阻单相接地故障。本方法可准确选出最高20 kΩ过渡电阻的接地故障。实验结果见表12。

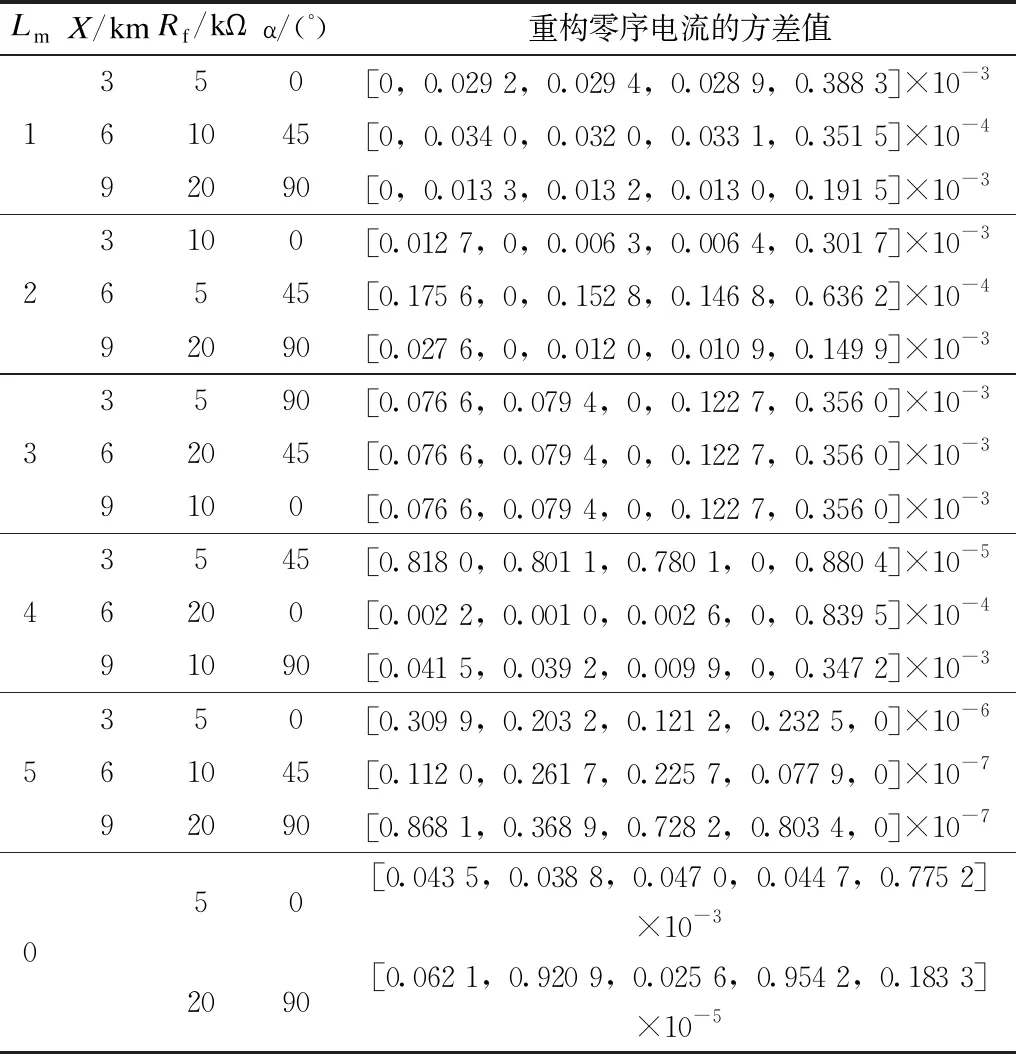
表12 高阻单线接地故障选线结果Tab.12 Line selection results of high resistance single wire grounding fault

高阻接地故障发生时，故障电流与零序电流都减小，故障特征也减小，使得使用能量为特征的选线方法的选线正确率下降。而缆—线混合线路改变了系统的阻抗，容抗增加且零序电流波形发生畸变，使得使用能量为特征与相关性为特征的选线方法准确率也下降。本方法将各馈线首端零序电流经过CEEMDAN分解后根据各分量贡献率提取独立成分分量，可识别出故障分量，选出故障线路。本文方法与零序电流的大小无关，只对各线路单通道首端零序电流分析，可对高阻接地故障选线。

4 结论

本文提出的基于自适应噪声完备集合经验模态分解与独立分量分析的故障选线方法，将馈线首端零序电流分解并根据贡献率通过独立成分分析构建独立成分分量。提出使用峭度判别线路零序电流成分并且重构零序电流。本方法可以使用于架空线路、缆-线混合线路的经高阻抗接地故障和相继接地故障。提出了按峭度值大小的“排序推拉”策略，可有效减少试拉闸操作，提高故障选线准确率。仿真表明该方法不受接地过渡电阻、位置、合闸角及噪声干扰等因素的影响，有较好的适应性。