思维导图在解题教学中的应用探讨*

广东省高州市高州中学(525200) 陈应全

1 问题提出

思维导图又称心智导图,是英国学者托尼·巴赞20世纪70年代提出的一种发散性的表达方式,它是一个将思维可视化、知识结构化的有效工具.近年来,思维导图在各行各业的应用越来越广,在数学教学中也得到了很多师生的认可并尝试应用.教师根据教学需要合理使用思维导图既能帮助学生形成一个完整的知识脉络,提升学习效率,又能帮助老师建立完善的知识体系,提升教学效果.

解题教学是高中数学课堂中的一种常规的教学行径,其目的是巩固基础知识,渗透数学思想方法以及发展数学核心素养.但是由于数学自身特点使得一些问题往往具有过多的思维量以及繁杂的运算量,致使不少学生在解题教学中难以理解问题解决的来龙去脉.而思维导图作为一种图像化思维工具,能有效地实现数学抽象思维可视化,构建清晰的知识脉络和推理形式[1].因此,探索思维导图在解题教学中的应用对提升解题教学的效果具有积极的意义.下面笔者结合多年的教学实践和思考,探讨思维导图在解题教学的中的应用,供同行参考.

2 教学探讨

2.1 利用思维导图帮助理解题意

解题教学的第一个环节是帮助学生分析题目条件,理清解题目标,以期寻找解题突破口.在这个过程中,思维导图可以充分凸显其可视化的优势.教师引导学生通过引入图形、文字与符号等,将题目中的文字语言利用数学语言表达,把题目中的关键词逐个解读或进行简单的推导,使题目中的条件与条件、条件与结论的关系更加清晰明了,有助于学生深入理解题意,为下一步探寻解题路径奠定基础.

例1(2021年全国甲卷(理)第12题)设函数f(x)的定义域为R,f(x+1)为奇函数,f(x+2)为偶函数,当x∈[1,2]时,f(x)=ax2+b.若f(0)+f(3)=6,则)

分析此题条件比较多,很多学生读完题目后往往难以理解条件之间的关系.为此笔者在教学过程中画出了该题的审题思维导图(如图1所示),帮助学生理解题意.

图1

从图1可以看出,在解题教学中,教师能合理使用思维导图将题目中条件间的关系、条件与结论关系梳理清楚,在思维导图中还结合相关概念对部分条件进行了简单的推导,有助于学生更深刻地理解题意,提高了审题效率.

2.2 利用思维导图探寻解题路径

罗增儒教授在《数学解题引论》指出:解题活动是一种思维活动,解题教学不仅要解题活动的结果(答案),而且要呈现解题活动的必要过程——暴露数学解题的思维活动[2].可是,不少老师在解题教学中仍然习惯采用“重结果,轻过程”的教学模式,缺乏解题思维过程的呈现,造成学生的思维能力得不到发展,这样的课堂致使学生未能真正掌握探寻解题路径的方法,从而形成教学中“老师讲的时候能听懂,自己做的时候就不会”的不良局面.为此,在解题教学中我们可以借助思维导图对题目进行层层剖析,让教师和学生一起从不同视角探寻解题路径,提高学生课堂参与度.整个思维过程充分暴露在思维导图上,不仅有助于学生梳理每种解题路径的来龙去脉,还可以明晰各种解题路径的优劣.

例2(2021年新高考I卷14)已知O为坐标原点,抛物线C:y2=2px(p＞0)的焦点为F,P为C上一点,PF与x轴垂直,Q为x轴上一点,且PQ⊥OP,若|FQ|=6,则C的准线方程为____.

分析本题求C的准线方程,难度并不大,通过题目条件建立关于p的方程即可.根据题意易知结合条件PQ⊥OP与|PQ|=6可建立关于p的等量关系,因此可以从勾股定理、直线斜率关系与平面向量知识多个视角思考.此外,结合条件PQ⊥OP与PF与x轴垂直也可从平面几何性质视角思考.此时,我们可以从这四个视角画出思维导图,如图2所示.

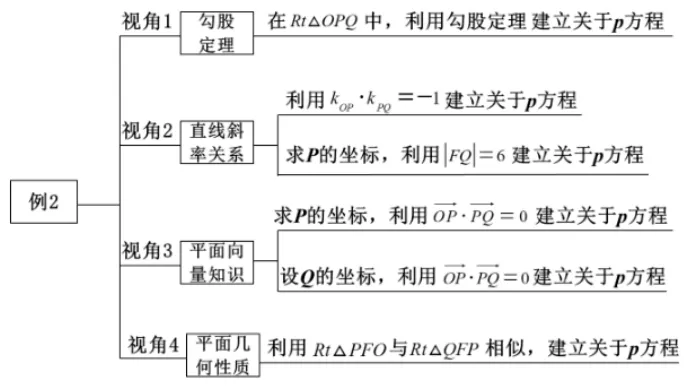
图2

本题利用思维导图作为工具探索解题路径,充分展示了解题思维过程,既有助于探寻多种解题路径,又有利于拓展学生思维.

2.3 利用思维导图进行变式拓展

在解题教学中,对例题实行变式拓展是一种常用手段,旨在优化学生思维品质,激发学生探索潜能以及提升综合解题能力.可是,有部分老师在变式拓展中变式拓展较多而未能暴露“变”的思维过程,使得学生未能领会到“变”的方向与本质.此时,教师可以引入思维导图既可以让学生深入思考、作笔记,以便课后复习,又可以让学生领悟到教师对例题“变”的过程,进而引导学生分析问题,解决问题并形成自己的解题思维.

笔者对本例题进行了九种变式拓展,从学生课堂反馈情况来看,其实很多学生不了解“变”的方向和本质.为此,笔者借助思维导图让学生领会“变”的思维过程,如图3所示.

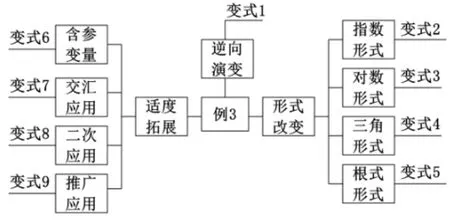
图3

将例题变式拓展与思维导图结合,能更好地体现变式拓展过程,以便学生能在更高的站位上理解问题,有利于学生构建知识网络,达到了触类旁通、举一反三的教学效果.

2.4 利用思维导图进行反思回顾

著名数学教育家波利亚“怎样解题表”的第四个步骤便是“反思回顾”,他还指出:通过回顾完整的答案,重新斟酌、审查结果及导致结果的途径,学生能够巩固知识,并培养解题能力[3].因此,反思回顾是解题不可或缺的重要环节,更是提升解题能力的重要途径之一.可是,不少老师在解题教学中往往过于草率而未能将反思回顾环节落到实处,常常简单地总结几句,留给学生的是一种走马观花的感觉.在解题教学中,教师不仅要向学生讲清楚解题后回顾反思到底“反思什么”,还要引导他们如何进行解题反思.一般地,我们可以引导学生反思该题答案的正确性、解答过程的严密性、解法是否具有推广意义以及相关注意事项等.下面利用思维导图结合例3,就利用基本不等式求最值有关问题作一个解题反思回顾,如图4所示.

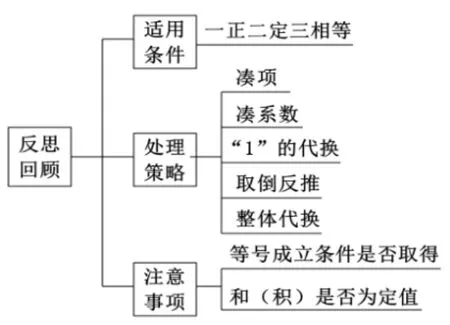
图4

在解题反思回顾中使用思维导图,可以说是对解题后的一个直观归纳总结,给学生创造了一个重要而有益提升解题能力的机会.

3 结束语

综上所述,思维导图可以广泛应用于解题教学中,由于其具有思维可视化、知识结构化的优势,有助于学生快速地理解题意,合理地探寻解题路径,规范地书写解答过程,深刻地理解例题“变”的本质,科学地进行反思回顾.事实上,教师不采用思维导图依然可以正常开展解题教学,但是借助思维导图之后,能引导学生进行可视化思考数学问题,促使学生对问题有一个“全景式”的把握,将学生的解题视野提升到更高的层次,从而有效地提升了学生数学综合解题能力.因此,思维导图作为一种有效的解题辅助工具,我们有必要将它应用于解题教学过程中,以便学生逐步养成运用“思维导图”解决数学问题的优越思维模式,从而提升我们的教学效果.