立足教材,重视本质——以问题中的基本图形与知识的分析为例

广东省广州市骏景中学(510650) 程 丹

1 基本图形

问题1已知,BC是圆O的直径,点A是圆上的点,满足AB=AC,点D是圆周上任意一点,试猜想BD、CD、AD三者之间的数量关系.

点评有两种情况.

(1)点D与点A在直径BC异侧(如图1),则连接AD,把ΔABD逆时针旋转90°至ΔACD′,从而得到BD+CD=AD(如图2);

图1

图2

(2)点D与点A在直径BC同侧(如图3),则连接AD,把ΔABD逆时针旋转90°至ΔACD′,从而得到BD−CD=AD(如图4).

图3

图4

教材来源2011版本人教版初中数学九年级上册第二十四章“圆”P87例题4.

教材例题如图5,在⊙O中,直径AB=10cm,弦AC=6cm,∠ACB的平分线交⊙O于点D,求BC、AD、BD的长;

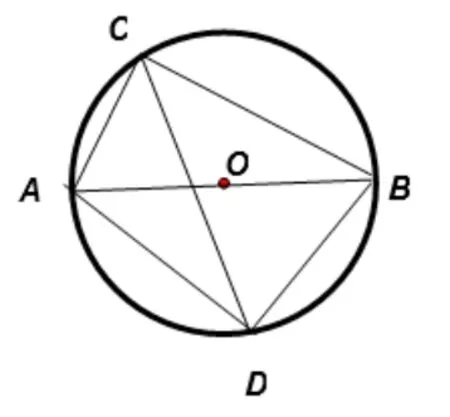
图5

变式已知条件不变,求CD的长.这样的问题就回归到基本图形1的第(1)种的情况.

问题2若BC不是直径,点D是劣弧BC上任意一点,∠BDC=60°,其他条件不变,请问结论会改变吗?答案是——会改变!

教材来源2011年人教版初中数学教材九年级上册P90习题14.

教材习题如图6,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°,判断ΔABC的形状,并证明你的结论.

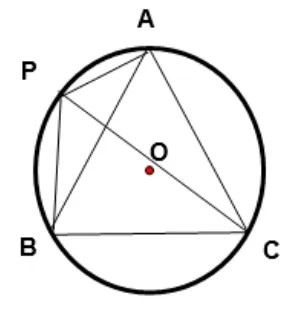
图6

变式1试猜想线段PA、PB、PC三者数量关系,并证明.如图7,根据旋转,易得PA+PB=PC.

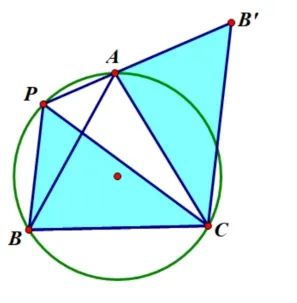
图7

变式2若点P是劣弧AB的中点,则线段AC、BC、PC三者之间的关系.如图8,根据旋转,易得AC+BC=

图8

首先,这两个基本图形的问题是来源于教材,教师要善于不断地挖掘教材,研究好教材的例题和习题.不要认为教材内容过于简单,不足以应付中考,我们教师一定要做好教材的再开发者.其次,这基本图形的立足知识点是旋转.教师要引导学生抓住基本概念的核心、基本问题的本质.旋转是九年级数学上学期的内容,是几何图形变换的最重要和常考的一种.教师引导学生从旋转的性质核心出发,旋转的三要素:旋转点、旋转角度、旋转方向.这两个问题的关键突破点就是以等腰三角形的顶点为旋转点,以等腰三角形的顶角为旋转角,找准要旋转的三角形,从而把所求的线段关系转化到一个三角形中的线段关系.教师要让学生学会不断回到概念中,从基本概念出发思考问题、解决问题,加强概念和基本知识联系性的教学,从概念的联系中寻找解决问题的新思路,找出通性通法.基础是发展的根本,根深才能长成参天大树,本固才能立于不败之地.

2 中考再现

例1(2020年.广州中考第24题)如图9,⊙O为等边ΔABC的外接圆,半径为2,点D在劣弧上运动(不与点A,B重合),连接DA,DB,DC.

图9

(1)求证:DC是∠ADB的平分线;

(2)四边形ADBC的面积S是线段DC的长x的函数吗?如果是,求出函数解析式;如果不是,请说明理由;

(3)略

点评本题第(2)问就是问题2的基本图形,关键得到AD+BD=DC.

例2(2018年.广州中考第25题)如图10,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.

图10

(1)求∠A+∠C的度数;

(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;

(3)略.

点评本题第(2)问就是问题2的基本图形的变式2,抓住条件AB=BC,利用旋转就可以突破和解决(如图11),从而得到AD2+CD2=BD2.

图11

例3(2016年.广州中考第25题)如图12,点C为ΔABD的外接圆上的一动点(点C不在上,且不与点B,D重合),∠ACB=∠ABD=45°

图12

(1)求证:BD是该外接圆的直径;

(2)连结CD,求证:=BC+CD;

(3)若ΔABC关于直线AB的对称图形为ΔABM,连接DM,试探究DM2,AM2,BM2三者之间满足的等量关系,并证明你的结论.

点评本题第(2)问就是问题1的基本图形.抓住这个本质,就可以对它迎刃而解.

第(3)问,关键抓住AB=AD,以及∠BAD=90°.利用旋转,把线段BM、AM、DM的关系,转化为同一个三角形中线段BM、MF、BF的关系,从而得到BM2+2AM2=DM2(如图13).

图13

3 思考与反思

3.1 重视教材、提升品质

从近几年广州个别中考题的纵向对比,笔者发现,这些题目问法新颖,考查了学生对新知识的探究能力和后续学习的能力与素养,考查了数学基础知识与思想方法的核心和本质.数学教学的目的是为了有效地促进学生学好数学、提高思维能力,培养理性精神.教师是教学的主导作用,教师要善于立足教材、挖掘教材、研究教材,立意中学数学知识的来龙去脉,对知识结构把握准确,对中学数学知识的思想方法运用自如,并且教师要学会纵向横向看中考新动态,结合教材和新课标研究中考新方向,这样才能让学生脱离解题的困惑和苦闷.教师引导学生用好教材的例题与习题,掌握好基本概念和规律,从而养成一个良好的数学学习习惯,提升学生的学习品质.

3.2 重视概念、提升思维

数学知识的本质是由数学概念和原理反映的数学思想方法来体现,知识结构之间的实质性的联系可以通过平时的数学思维训练体验,通过一定数学思想方法的训练达到培养学生数学思维品质,从而达到数学核心素养的渗透.初中阶段的学生,不能很好地理解抽象的概念,也不能很好地把握法则、定理背后规律性的东西.教师应该充分挖掘教材,启发和引导学生,让学生感悟这些概念和规律是从日常生活中数量关系、图形关系抽象出来的,鼓励学生学习的主动性,发展学生的个性,让学生掌握一些基本图形的理解和研究,有利于培养学生的几何直观和空间想象力,提升学生的思维能力.

3.3 重视本质、提升素养

数学教学是以基础知识、基本技能为载体,使学生牢固掌握基础知识、基本技能、形成基本能力和基本态度的过程教.数学本质是思维能力的培养、数学素养的提升,紧扣问题内在联系,教师在平时教学中,多立足教材、多挖掘教材例题与习题,抓住基础知识的联系与内涵,提升学生在新情景中运用基本知识解决新问题的能力,不断渗透数学几何直观核心素养的培养.