一类非对称圆锥曲线问题的解法研究
浙江省温州市第五十八中学(325000) 金荣杰
在圆锥曲线问题中,形如mx1+nx2(mn)或my1+ny2()的式子,通常是无法根据韦达定理直接求解,我们把这类问题称为非对称圆锥曲线问题,本文以一道期中考试题为例,探究这类问题的解法.
1 试题呈现
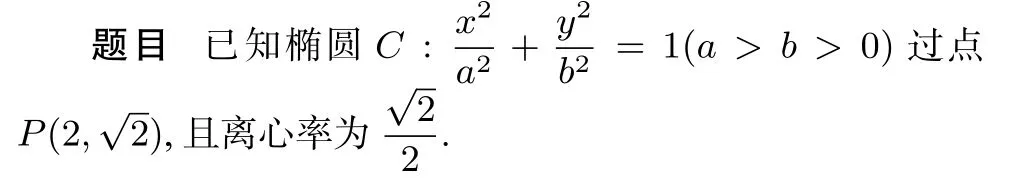
(1)求椭圆C的方程;
(2)设椭圆C的上、下顶点分别为A,B,过点(0,4)斜率为k的直线与椭圆C交于M,N两点.求证:直线BM与AN的交点G在定直线上.
2 试题分析

解题至此,学生发现2x1+6x2,3x2−x1没有办法直接利用韦达定理就放弃了.笔者经过一番探究,总结出解决此类非对称圆锥曲线问题的七种解法,供读者参考.
3 解法探究
3.1 关注特殊情形,先猜后证
分析特殊到一般是高中数学中的重要思想,对于圆锥曲线中的定值、定点、定线等问题,考虑直线的特殊位置,如直线过特殊点,顶点或者斜率不存在、斜率为0等情况,可以启发我们找到正确的结果,然后通过证明该结果对一般情形成立即可.这样可以明确解题的方向,降低题目的难度.

3.2 回归曲线方程,合理转化


3.3 引入待定参数,配凑常数
分析受方法一的启发,在②式两边配凑一个常数可以将非对称问题转化为对称问题,不同于先猜后证,下面我们尝试引入待定参数,使得x1,x2前的系数相等,进而确定参数的值.
解在②式两边加上参数m,则

3.4 配凑两根之和,消元化简
分析对于②式,最大的困难是如何处理式子2x1+6x2,3x2−x1,我们可以通过韦达定理配凑两根之和消去一个未知量,如消去x1,则2x1+6x2=2(x1+x2)+4x2,3x2−x1=4x2−(x1+x2).
解

注本题也可以消去x2,同理可得y=1.
3.5 妙用韦达定理,积转为和
分析解题经验告诉我们,齐次化往往可以简化问题,在②式中x1x2是二次项,其它都是一次项,于是想要将二次项x1x2转化为一次项,观察x1x2与x1+x2的结构可知,两者可以相互转化.

3.6 引入通法通解,暴力计算


下面提供两道非对称圆锥曲线问题,供读者练习.
1.已知椭圆C:=1(a>b>0)的左、右焦点分别为F1(−c,0),F2(c,0),M,N分别为左、右顶点,直线l:x=ty+1与椭圆C交于A,B两点,当t=−时,A是椭圆C的上顶点,且ΔAF1F2的周长为6.
(1)求椭圆C的方程;
(2)设直线AM,BN交于点T,求证:点T的横坐标xT为定值.
2.如图,在平面直角坐标系xOy中,椭圆C:=1(a>b>0)的离心率为右准线的方程为x=4,F1,F2分别为椭圆C的左、右焦点,A,B分别为椭圆C的左右顶点.

(1)求椭圆C的标准方程;
(2)过T(t,0)(t>a)作斜率为k(k<0)的直线l交椭圆C于M,N两点(M在N的左侧),且F1M//F2N.设直线AM,BN的斜率分别为k1,k2,求k1·k2的值.
本文从多种角度优化运算,如从特殊到一般的数学思想引导学生思考,寻找突破口;借助曲线方程、代数变形、和积关系的转换等方法将非对称圆锥曲线问题转化为对称问题进行求解.最后再给出两道同类型问题,让学生独立自主的体会一下处理非对称圆锥曲线问题的方法,拓展学生的思维、提高学生的核心素养.

