机车轴箱弹簧断裂失效分析及疲劳寿命评估

张子璠，王克肖，杨广雪

(1. 中车青岛四方机车车辆股份有限公司，山东 青岛 266111； 2. 北京交通大学 机械与电子控制工程学院，北京 10004)

0 引 言

轴箱弹簧作为连接车轴与构架的缓冲装置，它通过不间断地对能量进行储存释放，达到了有效缓解因轮轨激励而产生的垂向和横向振动对车辆的损害，保证车辆的平稳运行的目的。由于弹簧直接承受来自轮轨的高频振动，受交变载荷作用而出现疲劳断裂便成为弹簧的主要失效形式。因此，分析列车运行时弹簧的受力情况，对其进行失效分析，进而为后期进行弹簧的结构优化设计，保证列车的安全运行具有重要意义[1-3]。

王文静等[4]通过对弹簧断口分析，线路载荷测试以及有限元仿真，对轴箱弹簧的失效原因进行了分析；张伟龙等[5]针对某些大功率交流机车的轴箱弹簧出现断裂，结合弹簧设计标准以及有限元方法进行了失效原因分析并给出了改进措施；许娜等[6]采用有限元仿真的方法，对包含初始缺陷的弹簧进行寿命仿真，获得了弹簧寿命随磨损深度的变化规律；尹太国[7]通过建立包含弹簧的车辆系统动力学模型，分析了轮轨中高频激励下弹簧的动力响应，并给出了降低应力的措施。

针对机车轴箱弹簧出现疲劳断裂的事故，首先进行了断口分析，确定了其失效特征。其次开展了线路动应力测试，获得了运用工况下的弹簧动应力响应特征并计算了疲劳等效剪应力。最终结合有限元模态分析确定了弹簧疲劳断裂的起因。

1 失效分析

1.1 宏观断口分析

断裂失效的弹簧照片如图1。由图1可以看出，弹簧断裂于底座第2圈头部附近，弹簧断裂位置底圈的接触面上存在较为明显的磨损痕迹。断口与弹簧横截面约呈45°，无明显塑性变形痕迹。图2给出了弹簧断口的宏观形貌。由图2可以看出，断口上有明显的收敛放射线特征，断口开始于底圈的接触位置，裂纹起源位置磨损严重，附近可见大量的疲劳弧线。断口裂纹萌生区的外圆表面有一定程度的磨损特征。疲劳扩展区面积较小，存在一定量的疲劳弧线。断口其余区域为瞬断区，为典型的剪切唇形貌，具有反光小刻面特征。且扩展区有明显的黑色或褐色的色差，表明疲劳裂纹在表面形成，造成疲劳裂纹源扩展区与外界相通，断口表面受到空气、水、水蒸气及其他介质的氧化或腐蚀，以致断口上呈现黑色。

图1 弹簧断裂位置

图2 弹簧断口

1.2 微观断口分析

断口裂纹起源位置磨损严重，局部可见少量疲劳条带特征；疲劳裂纹扩展区可见大量疲劳条带特征，断口疲劳扩展区微观形貌如图3。

图3 疲劳扩展区微观形貌

2 理论计算

2.1 弹簧受力分析

由相关文献可知，当弹簧受垂向载荷为F时，弹簧圈的任意横截面的受力可简化为一扭矩和一切向力，这两种力系的效果是在截面产生纯剪应力，对于圆截面簧丝，剪应力的计算式为：

(1)

式中：K为曲度系数；D为弹簧中径；F为垂向载荷；d为簧丝直径；π为圆周率。

2.2 弹簧应力测试方法

由2.1节内容可知，弹簧在受垂向力的前提下，其截面仅存在剪应力，并且由于列车运行时，弹簧承受交变垂向力，其剪应力也为交变应力。此外对于实际测量结构应变时，只能够测到结构的表面应力，因此，准确测量弹簧表面的剪应力是精确评估其疲劳寿命的前提。

假定弹簧的表面应力状态为平面应力状态，工程上为测量平面应力条件下的剪应力，通常采用应变花作为传感器。选择的应变花形式为直角应变花，可测量0°、45°及90° 3个方向的线应变。由于平面应力状态可以通过2个正应力σx、σy(正应变εx、εy)和一个剪应力τxy(剪应变γxy)确定，因此对于直角应变花，通常假定0°方向应变为εx，90°方向应变为εy，则γxy可通过计算得出，具体计算过程为：

假设正应变(εx、εy)和剪应变(γxy)已知，并存在与x轴夹角为α的垂直于表面的平面，则该平面内的剪应变τα及其法向应变σα可通过式(2)、式(3)得出：

(2)

(3)

该平面的主应变方向由式(4)进行计算：

(4)

对于直角应变花的情形，则根据式(2)，可得到45°方向的应变表达式为：

(5)

将式(5)简单变形可得到γxy为：

γxy=ε0+ε90-2ε45

(6)

根据弹性力学理论，可得剪应力为：

τxy=Gγxy

(7)

式中：G为材料的剪切模量；π为圆周率。笔者测试的弹簧材料为51CrV4，其剪切模量取值为80.79 GPa。

取弹簧内圈表面黏贴应变花处一微元进行受力分析，应力状态如图4。由图4可知，τxy即为弹簧截面上的剪应力。

图4 微元体受力分析

对于纯剪应力状态，εx和εy为0，即式(4)的结果为负无穷，表明主应变的角度为-45°或者135°，这与裂纹扩展平面的角度一致，表明弹簧沿着最大主应变所在的螺旋面方向断裂。

2.3 疲劳寿命分析

通过2.2节的过程对测试数据进行计算后，得到交变剪应力的时间历程，进而采用雨流循环计数方法对剪应力时间历程进行循环计数，可以得到剪应力的应力谱，每一级应力谱的剪应力为恒幅应力。将以应力谱形式表示的多级应力按照损伤一致的准则等效为单级恒幅应力，称之为等效应力幅。将等效应力幅与结构在相同工艺条件和指定可靠度下的疲劳极限(称之为疲劳许用应力幅)进行比较，可以评估结构在一定的运用条件和指定可靠度下的疲劳强度[8]。

本研究采用Miner线性疲劳累计损伤法则和弹簧的S-N曲线参数计算等效剪应力幅。根据Miner法则，第i级应力τi循环ni次造成的损伤为：

(8)

式中：m和C为S-N曲线参数。

若应力谱共有I级，则总损伤按照式(9)计算：

(9)

假设列车服役期间每公里造成损伤保持一致，则服役结束时总损伤为：

(10)

式中：L为服役运用公里数；L1为实测公里数。

令列车达到服役里程时，等效应力循环N次，则D′可表示为：

(11)

联立式(8)～式(11)，可以得到等效应力幅τaeq的计算表达式为：

(12)

式中：N为疲劳极限所对应的应力循环数。

机车的服役寿命约为600×104km，分别代入τaeq表达式，就可计算得出对应整个寿命期运行里程的等效应力幅。对于51CrV4，参阅相关资料可知其m=5，N=1 000万次循环。

根据EN13749标准规定在测试弹簧的抗剪疲劳极限时，应不出现明显的接触磨损现象，而由上文的失效分析可知，运用中的弹簧存在较为严重的磨损，因此计算疲劳极限时要考虑由于支撑圈和有效圈之间的接触摩擦产生表面不平、缺口应力集中，甚至会出现微动磨损的影响[9]。通过查阅相关资料可知，弹簧的抗剪切疲劳极限为250 MPa，表面粗糙度的影响系数取0.9，缺口导致的应力集中影响系数取0.8，微动磨损的影响系数为0.8，最终得到降低后的疲劳极限为：

τlit=250×0.9×0.8×0.8=132.84 MPa

3 线路测试及模态计算

3.1 传感器布置

在弹簧的关键部位黏贴应变花的方式测量列车运行时的应力时间历程，测点布置方案充分考虑到弹簧的结构、工艺特点以及出现过裂纹的区域。最终选择的测试弹簧位置如图5。由于弹簧内侧空间有限，不利于布置应变花，此外由内侧引出的导线也会由于弹簧压缩而被破坏，因此将应变花布置在弹簧外表面。图5中B端代表列车前进位置，弹簧位于转向架的第4根轴外侧，靠近减振器一侧。应变花布置在一系弹簧下部端圈与有效圈接触区域，如图6。测点照片如图7，应变花的布置、标定以及传感器线缆的安装在车辆段完成。

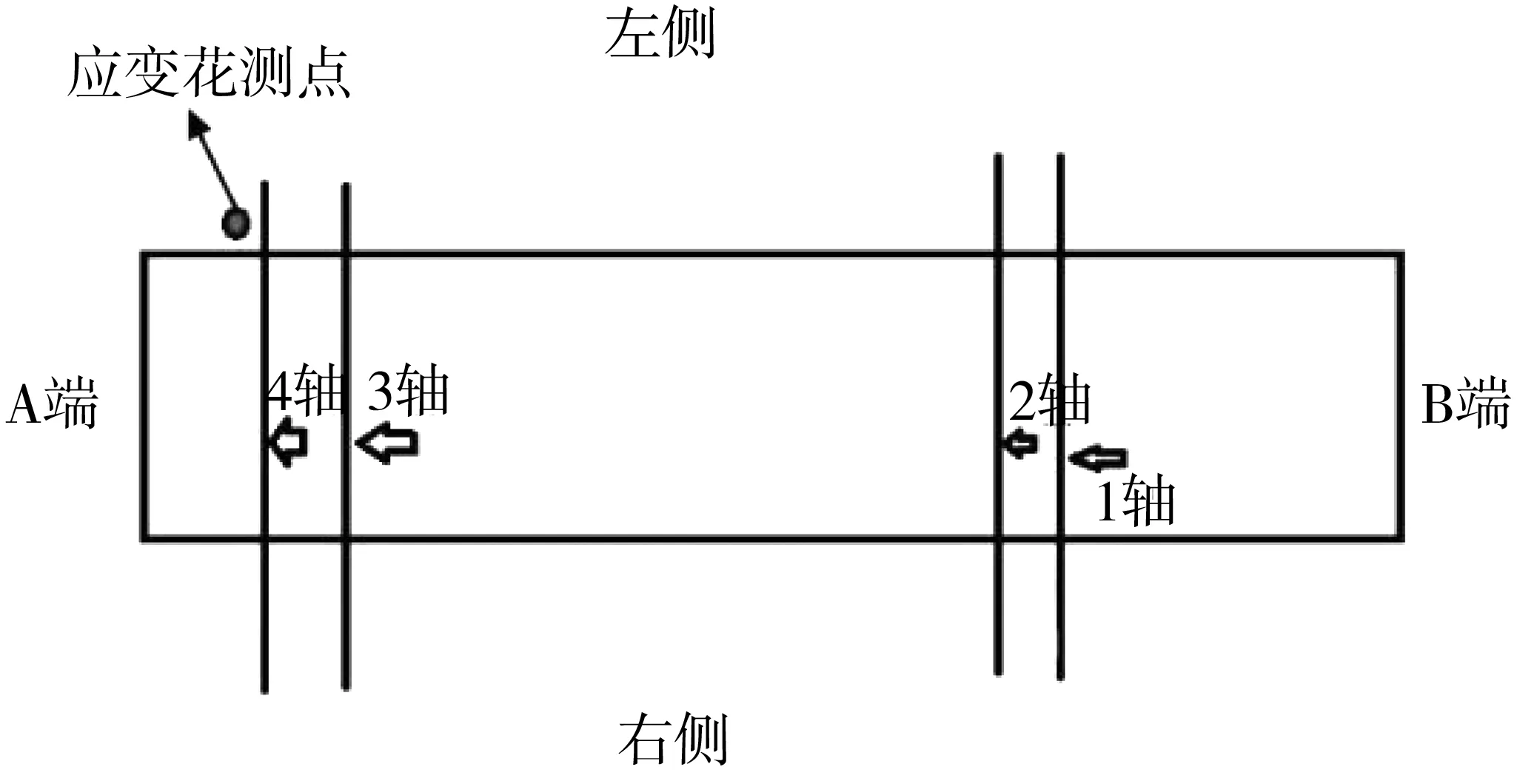
图5 测试弹簧位置

图6 应变花布置位置

图7 测点照片

数据采集系统选择高可靠度的Somat eDAQ数字式信号采集仪，该仪器适用于强振、温度变化范围广等恶劣条件下的长期无人测量，同时配备大容量存储器保证记录下完整的测试数据。由于测试过程中或多或少存在噪声干扰，采集到原始信号之后，还需要进行进一步的降噪处理得到纯净的信号，以用于后期的疲劳寿命评估。测试线路选择西安至安康区间，为了使测试尽量覆盖到机车运行的完整工况，此次测试历时一个月，期间轮对经过一次镟修。

3.2 数据分析

图8给出了镟轮前应变花测点的三向应力的时域波形以及频谱图。从镟轮前的测试结果来看，一系弹簧测点45°方向的频率除了1～5 Hz的低频为主之外，存在90 Hz左右的高频信号，同时结合时域波形可以看出出现高频成分的测点波形存在谐波情况，而0°及90°方向的频率并未出现90 Hz的高频成分，并且时域波形无明显谐波。图9给出了镟轮前合成的最大剪应力的时域波形以及频谱图，可以看出，同45°方向应力类似，剪应力存在90 Hz左右的高频信号，对应的时域波形表现为谐波形式。

图8 应力时间历程及频谱

图9 剪应力时间历程及频谱

图10给出了镟轮后应变花测点的三向应力的时域波形以及频谱图。从镟轮后的测试结果来看，一系弹簧各方向均已无明显的高频成分，信号主频以1～5 Hz的低频为主，同时结合时域波形可以看出测点波形无谐波情况。图11给出了镟后合成的最大剪应力的时域波形以及频谱图，可以看出，合成后的剪应力也无明显的高频成分，信号主频以1～5 Hz的低频为主，同时结合时域波形可以看出测点波形无谐波情况。以上结果表明镟轮可以有效降低弹簧的高频成分。

图10 应变花应力时间历程及频谱

图11 剪应力时间历程及频谱

对镟轮前后的剪应力时间历程进行雨流计数并计算等效应力，结果如图12。由图12可以看出，镟轮前的等效应力值较大为229.98 MPa，已远远超出疲劳许用应力132.84 MPa；镟轮可以大幅降低测点的等效剪应力，由镟轮前的229.98 MPa下降到89.45 MPa，降低了61.11%，低于疲劳许用应力。

图12 镟轮前后等效应力

3.3 失效原因分析

由以上测试结果可以看出镟轮对弹簧的等效应力幅值有较大的影响，第4根轴的测点出现弹簧等效应力幅值超出疲劳许用应力的情况，这也是导致弹簧在运用过程中出现过早疲劳断裂的原因。镟轮能使该测点的等效应力幅值大幅降低，镟轮后基本上等效应力能恢复到较低的水平。而镟轮前后的应力响应仅仅是92 Hz处存在差异，因此推测镟轮前弹簧存在的92 Hz高频是导致等效应力异常增大的主要原因。首先需要确认此频段是否为弹簧固有频率，根据结构动力学理论，结构的自然振动的频率和振型可以通过模态计算获得，因此需要对弹簧进行模态分析。由于弹簧固定在构架和轴箱之间，为准确模拟弹簧的受载情况，对弹簧上表面进行除垂向外的全约束，下端建立全约束。笔者采用有限元方法，通过对弹簧三维结构进行网格划分，依照动力学方程，求得结构的固有振动频率和振型。

采用有限元法对弹簧进行约束模态计算，得到弹簧前8阶模态主频如表1，由表1可以看出，弹簧第3阶模态主频为91.86 Hz，接近实测应力的92 Hz，图13给出了弹簧第3阶和第4阶约束模态的位移振型图。以上结果表明外部激励频率已经接近弹簧固有频率，从而引发了结构共振导致应力增大。

图13 弹簧模态振型

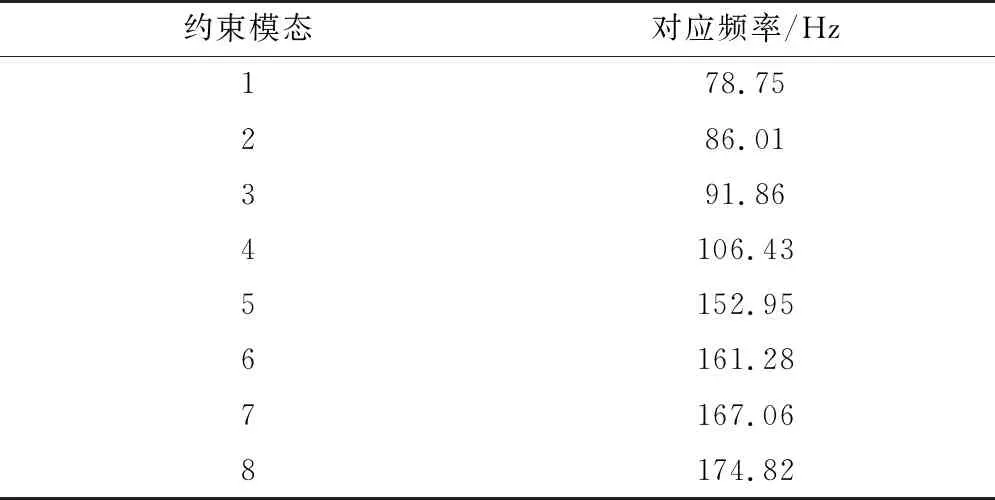
表1 弹簧模态主频

为进一步探究外部激励包含的92 Hz的频带的来源，笔者计算了轮对多边形引发的振动频率，轮对多边形阶数n与其激发的频率f可由式(13)计算：

(13)

式中：D为轮对名义滚动圆直径，取0.76 m；v为列车运行速度；π为圆周率。

结合列车的速度信号计算可知，列车正常运行时的行驶速度为72 km/h左右，将其与弹簧的92 Hz频率成分代入式(13)，可得轮对的多边形阶数位于17～19阶之间，因此有可能是轮对多边形带来的振动信号，激发了弹簧在92 Hz左右的固有频率，导致了振动能量放大。为了验证此猜想，后期调用了车辆故障记录，找到了此车第4根轴的19边形处报警，进一步验证了轮对不圆引起弹簧共振导致应力增大的猜想。

除此之外，通过观察弹簧断裂位置可知，弹簧断裂位置基本都是位于弹簧接触线区域，如图14。如前文所述。接触磨损会导致弹簧的疲劳强度降低，因此，弹簧断裂可归结为接触磨损导致疲劳强度降低与发生模态共振导致动态应力异常增大。

图14 弹簧断裂位置

4 结 论

针对某型机车轴箱弹簧出现断裂的现象，采用断口分析、线路动应力测试以及有限元仿真方法，探究了裂纹的成因。主要结论为：

1)由断口分析结果可知，弹簧失效为疲劳断裂失效模式，裂纹源始于底圈的接触磨损位置，疲劳扩展区所占面积较小。

2)镟轮前合成剪应力以92 Hz的高频谐波为主，而镟轮后合成剪应力以1 Hz左右的低频成分为主。结合车速计算可知，92 Hz频率与车轮19边形激扰频率相符。

3)镟轮前的600×104km等效剪应力值为229.98 MPa，高于疲劳极限约73.13%；镟轮后为等效应力值为89.45 MPa，降低了61.11%，并且低于疲劳极限。以上结果表明镟轮可大幅降低等效剪应力。

4)弹簧第3阶约束模态主频为91.86 Hz，接近实测应力的92 Hz，外部激励频率接近弹簧固有频率，从而引发了结构共振导致应力增大。

5)弹簧断裂位置都是位于弹簧接触线区域,综上所述弹簧断裂可归结为接触磨损导致疲劳强度降低与发生模态共振导致动态应力异常增大。因此后期运用中，可考虑缩短镟轮周期以避免弹簧由于共振导致的疲劳断裂事故。