基于双向拍卖机制的共享泊位分配与定价研究
韩 艳,段晓宁
(北京工业大学 交通工程北京市重点实验室,北京 100124)
0 引 言
面对城市日益突出的停车问题,基于停车共享理念,充分利用现有停车位资源的方法受到广泛关注。北京、上海等地出台共享停车相关政策及措施,泊位共享主要涉及3个参与方:停车管理平台、泊位提供者(O-user)和泊位使用者(P-user)[1]。其中,停车管理平台以统一的租购价格向O-user租购停车泊位,再以统一的停车价格向P-user共享。处于推广阶段的共享停车存在以下问题:统一的泊位租购成本、停车价格忽略了O-user和 P-user的价格意愿,导致O-user收益和P-user出行效用无法达到预期,降低了O-user、 P-user和管理者参与泊位共享的积极性。为解决上述共享泊位定价和收益分配问题,国内外学者引入了拍卖机制(单、双向拍卖)[2-4]。
近年来,拍卖机制应用于电力市场、鲜花市场等行业和问题中,XIAO Haohan等[2]首次将双向拍卖机制应用于共享停车,并在充分考虑停车时间的基础上,提出两种“P-user竞争填充”拍卖机制。现有的共享泊位双向拍卖机制包括3方:停车管理平台、O-user和P-user,其中停车管理平台负责收集投标信息、泊位分配和定价,O-user和P-user根据出行需求向停车管理平台提交投标信息,包括停车时间、投标价格[2]。在定价方面,E.MASKIN等[5]、R.MILG-ROM等[6]认为顺序拍卖是最有利的拍卖机制。为保证社会福利最大,VCG 拍卖定价机制被提出[7-9],该机制既可以满足社会福利最大,又能够鼓励用户可信竞价[10],多被应用于计算用户的最终支付价格。
现有的非拍卖机制下共享资源分配研究多以用户效益或者系统效益最大化为目标,较少综合考虑参与者(O-user和P-user)的价格、泊位空间、时间要求等个体意愿,而基于拍卖理论的“共享泊位的分配”能够考虑O-user、P-user双方的价格意愿。谭冰清[11]在经典的第一、第二价格密封拍卖机制的基础上,提出了第m价格、第m+1价格密封拍卖机制,即顺序拍卖价格机制确定停车位的价格与分配;王雅娟等[12]利用在线拍卖方法,基于运输时间、服务质量等多属性要求,对运输服务采购机制进行了研究;X.T.R.KONG 等[13]研究基于单边拍卖的共享泊位分配机制,构建VCG模型求解泊位的合理定价;王鹏飞等[14]以存在多个地块的区域为对象,根据出行者对不同地块及停车时间模式的选择偏好构建了停车许可证的最优分配及定价模型,并利用Benders 分解原理、对偶理论及新型升价拍卖代理系统构建调优法对停车许可证进行拍卖。拍卖机制的泊位分配研究重点考虑P-user单边的意愿,较多关注停车时间因素,包括停车时长、停车起讫时间等,较少考虑泊位的空间特性(停车场至目的地距离)。
综上,现有研究在拍卖机制设计及其资源分配、支付规则方面取得了显著的成果,但仍存在以下不足:①现有拍卖模型中多考虑参与者(O-user和P-user)对共享泊位的时间属性,不能满足P-user对空间属性(停车场至目的地距离)的要求;②按照拍卖机制规定,P-user需按时到达停车场,但受路况、前序活动完成情况的不确定性影响,P-user入场时间和预定时间存在差异,即存在共享停车服务时间弹性调整需求。
为解决以上问题,可从考虑用户车位空间属性和服务时间弹性调整需求出发,优化制定共享泊位双向拍卖机制,以及开展相应的共享泊位分配及定价问题,这两方面着手。需考虑泊位空间属性和服务时间弹性调整需求,设计共享泊位双向拍卖机制,构建基于泊位空间属性和服务时间调整需求的共享泊位分配及定价模型。
根据上述问题,笔者考虑到供需双方的价格意愿、位置要求、停车时长、服务时间弹性调整需求等因素,设计预约模式下停车位共享的双向拍卖机制,以最大社会福利为目标,建立共享泊位分配模型,基于VCG模型测算O-user和P-user交易支付价格,设计算法并开展算例分析。
1 考虑共享泊位时空属性的双向拍卖机制设计
1.1 问题描述与说明
1.1.1 问题描述
共享泊位双向拍卖机制场景如下:多个O-user和多个P-user的竞价依赖于一个“停车管理平台”, 其中停车管理平台负责收集投标信息、泊位分配和定价,多个O-user和P-user分别向平台提供泊位供给和需求信息,平台依据给定的交易规则对供给信息和需求信息进行匹配,确定拍卖结果。双向拍卖机制场景如图1。
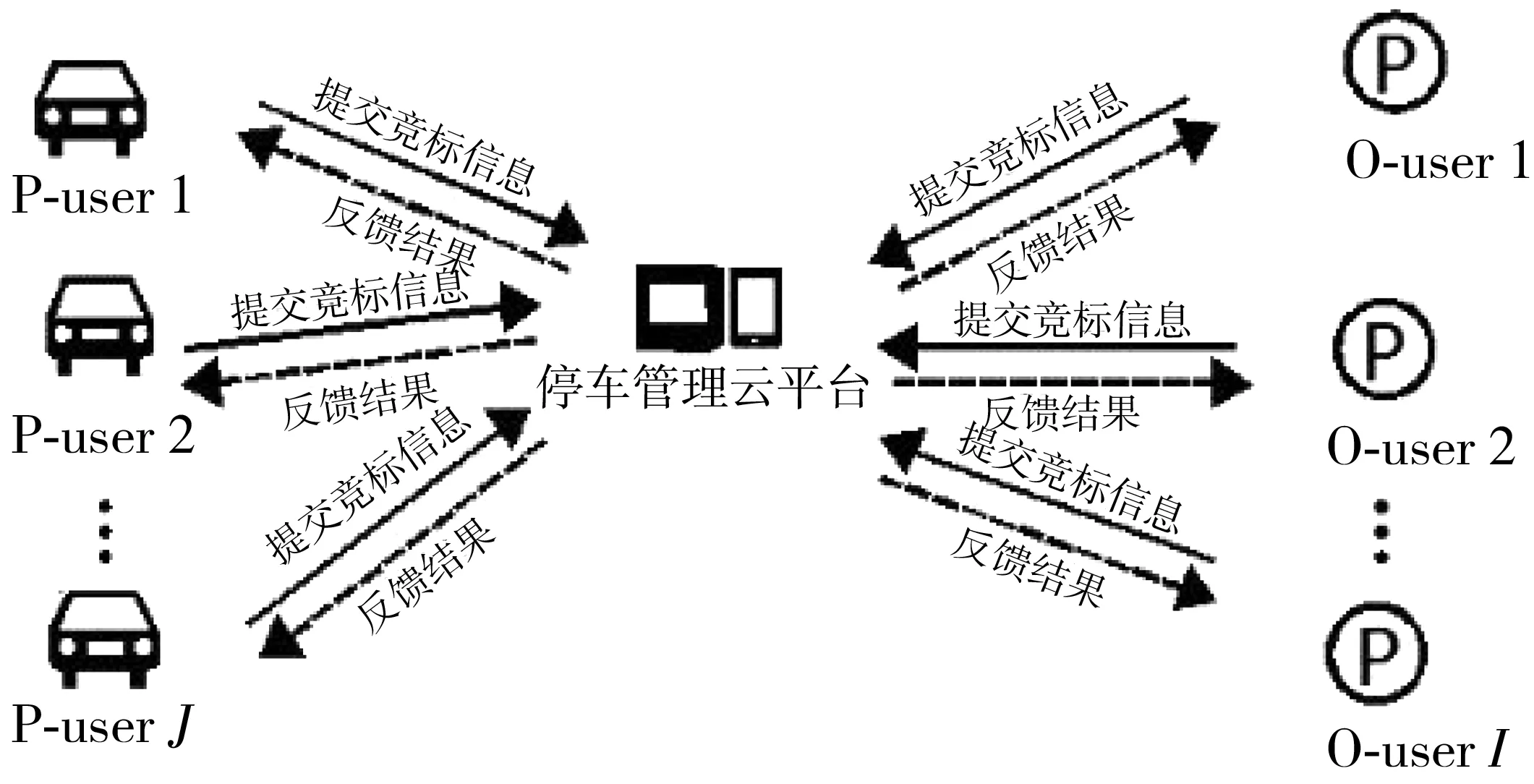
图1 双向拍卖机制场景
双向拍卖机制满足3个经济属性:①激励相容:参与者均能如实反映自己对物品价值的估计; ②个人理性:每个参与者的效用非负;③预算平衡:停车管理平台的收益非负。
1.1.2 基本假设
1)每个O-user、P-user都拥有自己对车位的私人预约值,该值将涵盖支付/接受意愿、时间差异和泊位空间属性等。
2)忽略泊位在停车场内部的位置分布,所有泊位的使用权对O-user、P-user来说是同质的。
3)“全有全无”原则:若平台不能满足该P-user的所有停车时间,则该P-user最后交易失败。
4)“多对多”原则:为提供灵活的匹配方案,增加交易规模,允许将一个O-user提供的停车位使用权分配给多个P-user,每个P-user的停车时间可以分割给多个O-user。
5)单一报价原则:在同一轮的拍卖中,O-user、P-user只能提交一个单价报价。
6)最小使用时间单元:假设平台上P-user停车时间和O-user出租共享泊位的使用时间最小为0.5 h。将一天 24 h依次编号为:时间单元 1~48。
7)P-user和O-user都遵守拍卖机制规定,按时到达或离开停车场。针对P-user共享停车服务时间可弹性调整的情况,系统允许P-user提交可接受的停车服务时间调整范围。
1.1.3 基本信息
共享泊位拍卖涉及O-user、P-user、停车管理平台3方参与者,3者均需提供或处理一定信息,作为拍卖机制的信息基础。
1)对某个O-useri需要提交的信息有:泊位所在停车场位置(xi,yi)、停车单元(ηi)、泊位共享时间ti、投标价格pi(每个停车单元)。
2)对某个P-userj需要提交的信息有:投标价格pj(每个停车单元)、停车时间tj、可接受的服务时间调整范围t′j、出行目的地位置(xj,yj)、可接受的停车后步行距离dj。
基础信息中“停车时间tj、可接受的服务时间调整范围t′j”意为P-user在平台上选择需要的泊位使用时段,并选择是否接受调整服务时间,若接受,输入允许调整的服务时间范围。由于过大的服务时间调整影响P-user的出行计划,因此设定P-user可接受的服务时间调整不超过1个时间单元。供P-user选择的允许调整的服务时间范围选项有: 0(不调整)、0.5、1个时间单元。
基础信息中“停车后的步行距离”是指停车场出口至目的地位置间的步行距离。鉴于停车选择行为特征分析研究表明,最大可接受停车场至目的地步行距离不宜超过 500 m[15],因此只考虑停车可接受步行距离在500 m 内的P-user,交易平台中对P-user提交的停车可接受步行距离信息设置可选项,分别为:小于50 m、小于100 m、小于300 m、小于500 m共4个选项。
3)平台处理的信息主要包括O-user和P-user位置信息转化、双方泊位、时间单元匹配。
共享泊位双向拍卖过程如图2。拍卖过程分为3个步骤:①O-user和P-user提交竞价信息;②停车管理平台进行决策分析;③输出交易结果。

图2 共享泊位双向拍卖机制流程
1.2 双向拍卖机制流程
Step 1O-user和P-user提前一天上传竞标信息。
Step 2时间匹配。判断每个P-user的停车时间间隔是否超过O-user所提供的最大停车时间间隔,若超过,则淘汰该P-user。
Step 3停车场匹配。输入各P-user的目的地位置、P-user可以接受的最大停车步行距离和平台上的停车场的位置,根据P-user提供的信息以及平台上停车场的位置信息判断是否存在符合P-user需求的停车场。输出符合各P-user需求的停车场集合。
Step 4统计经Step 2、Step 3后剩余的P-user,计算其支付价格,如果其投标价格小于支付价格,则淘汰P-user,否则进行交易。更新P-user集合。
Step 5根据以上4步,求得各P-user匹配的停车场集合Dj,推出停车场k剩余的P-user编号集合Tk,确定各P-user停车时间需求的O-user集合,求得停车场k的第n种P-user和O-user组合的社会福利(模型1),所对应的供需匹配及挪车次数情况。重复该步骤X次,直至求得社会福利最大的情况,且该种情况为其他与之社会福利值相等的情况中,挪动次数最少。
Step 6计算每个O-user 租购价格、P-user停车支付价格、平台收益。平台收益计算公式如下:
(1)
式中:U为平台收益;qj为P-userj(j∈J)停车支付价格;qi为O-useri(i∈I)租购价格。
2 基于共享泊位时空属性的最优泊位分配-定价模型及算法
1)最优泊位分配模型
研究的拍卖场景为停车管理云平台,由I个O-user和J个P-user组成,以社会福利最大为目标进行泊位分配。
社会福利最大化的目标函数为:
(2)
约束函数为:
(3)
(4)
0≤αij≤min{mj,Yi},i∈I,j∈J
(5)
0≤ηi≤yi,i∈I
(6)
0≤ξj≤1,j∈J
(7)
式中:mj为P-userj(j∈J)需要的停车单元;pj为P-userj(j∈J)投标价格;w为时间价值;s为目的地至停车场步行距离;v为行人平均步行速度;ηi为O-useri实际提供的(i∈I)停车单元;Yi为O-useri可提供的停车单元;pi为O-useri(i∈I)投标价格;αij为P-userj和O-useri交易的停车单元。约束(3)表示P-userj是否竞价成功,若ξj=1,则竞价成功,若ξj=0,则竞价失败;约束(4)表示每个O-user实际出租的停车单元等于该O-user交易的总和;约束(5)表示P-userj和O-useri之间的交易单位不能超过最大可交易单位; 约束(6)和(7)分别分别表示O-user和P-user所提供或需要的车位使用权单位数不超过自身所有或所需。
2)最优定价模型
在求得泊位最优分配方案的前提下,每个O-user和P-user会获得/支付相应的费用。VCG 理论下,用户的支付价格与自己出价无关,而是由市场决定,激励用户真实报价,保证机制可信。式(8)、式(9)分别为P-userj支付价格(qj)和O-useri租购价格(qi)的计算公式。
qj=mjpj-[V(I,J)-V-j(I,J)]
(8)
qi=ηipi+[V(I,J)-V-i(I,J)]
(9)
式中:V-j(I,J)为P-userj不参与拍卖机制时的社会福利;V-i(I,J)为O-useri不参与拍卖机制时的社会福利。
在建立优化模型的基础上,采用动态规划算法[16],根据各个O-user、P-user的满足状态,分析不同供需方匹配结果时的社会福利,直至求得社会福利最大的情况。
3 算例分析
3.1 算例数据
设定P-user和O-user参与人数I=J=10位,停车场数量共计5个,参数设置如表1和表2。其中服务时间调整范围+1表示P-user可以接受服务时间向后调整1个时间单元,反之,可接受向前调整1个时间单元。
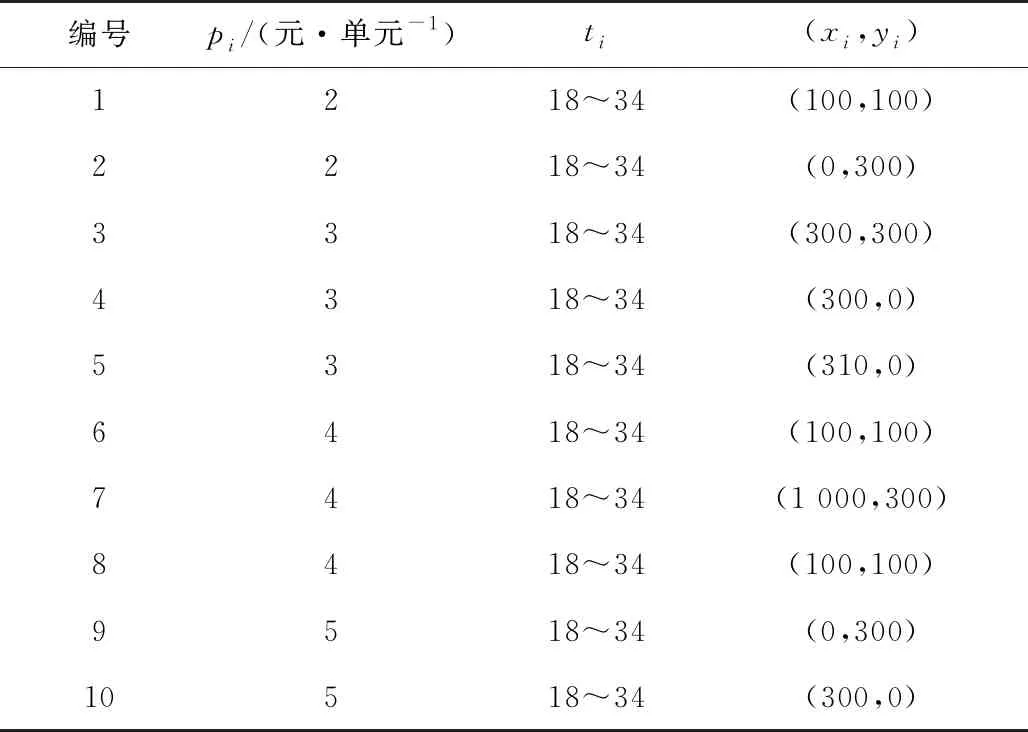
表1 O-user提供信息表

表2 P-user提供信息表
3.2 结果分析
O-user和P-user时间单元匹配结果、最大社会福利及平台收益求解结果如下:
1)P-user筛选结果
由于平台无法满足P-user 10位置需求,因此P-user 10退出拍卖系统;由于时间需求超出系统所能提供范围,P-user 9退出拍卖系统。
2)O-user筛选结果
由于供给泊位位置没有需求响应,O-user 3 、7、10退出拍卖系统。
3)具体供需时间单元匹配结果如图3,如P-user 1结果表明20~23单元分配给O-user 1,24~28单元分配给O-user 6。P-user总的挪车次数为5 次(P-user1、3、6、8在停车程中需要进行挪动);P-user 8的停车服务时间向前调整1个时间单元。
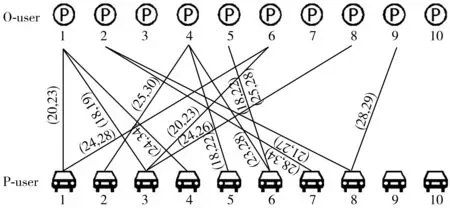
图3 供需时间单元匹配结果
4)价格与收益结果
经式(2)计算,最大社会福利为563元;经式(8)计算,P-user停车价格合计为627元;经式(9)计算,O-user租购价格合计为388元;经式(1)计算,平台收益为239元,O-user、P-user个体净收益结果如表3。

表3 个体净收益结果
由表3可知:O-user和P-user获得的净收益值均为非负值,笔者构建的双向拍卖机制可以实现供需双方时间单元的匹配,并保障了停车出行者和平台利益。
3.3 与传统停车共享模式对比
3.3.1 停车场基础数据
“淘车位”停车、“小强”停车等目前应用较为成熟的共享停车预约平台,属于固定价格的停车共享模式。P-user可通过该应用查询剩余停车位数量、收费标准等信息,进行提前预约或实时预约停车位。泊位租购价格qi低于O-useri投标价格pi,停车支付价格qj应高于泊位租购价格qi及P-userj投标价格pj,假设同一停车场内minpi/qi=1.5,qj/qi=1.2,(xk,yk)为共享停车场位置,如表4。

表4 停车场收费标准
现有的非拍卖机制下的共享停车关于分配规则有以下两点假设:
1)若有多个P-user竞争同一停车场同一时段泊位使用权,则泊位估值最高的P-user获得使用权。
2)所有P-user在停车场位置、时间单元均满足要求的情况下,均选择价格在估值范围内的且最低的停车泊位。
3.3.2 结果分析
由1.2节各拍卖流程计算具体供需时间单元匹配结果如图4。

图4 传统共享模式停车单元匹配结果
1)P-user筛选结果
由于平台无法满足P-user 10位置需求,因此P-user 10退出共享系统;由于时间需求超出系统所能提供范围, P-user 9退出共享系统。综合考虑P-user 2、6、8的可接受步行距离、可接受价格,各个停车场均不符合要求,因此退出共享系统。
2)O-user筛选结果
由于供给泊位位置没有需求响应,O-user 2、3、7、9和10退出共享系统。
3)经式(1)计算,平台收益为41元。
由图4可知:传统共享模式中,编号为 1,3,4,5,7 一共5位P-user和编号为 1,4,5,6,8 一共5位O-user成功交易,而双向拍卖机制中成功交易P-user共8位,O-user共7位。
双向拍卖机制与传统共享模式对比如表5。

表5 双向拍卖机制与传统共享模式对比
由表6可知:①交易成功率方面,双向拍卖机制比传统共享模式提高25%;②在P-user成功交易的时间单元数占需求总数的比例上,双向拍卖机制比传统共享模式提高28%;③平台收益方面,双向拍卖机制比传统共享模式增加198元。因此双向拍卖机制可以实现更多的时间单元匹配,提高交易成功率和平台收益。
4 结 论
针对车位分配规则和交易支付规则的共享车位问题,提出了基于泊位空间属性及服务时间弹性调整需求的的双向拍卖机制,在考虑出行者在泊位空间属性、服务时间弹性调整的基础上,基于激励相容、个体理性和预算平衡3个经济特性,基于出行者在停车时间、泊位空间属性、服务时间弹性调整的选择偏好,构建了以社会福利最大化为目标的共享泊位分配与定价模型。与现有停车共享模式进行对比,数据显示,双向拍卖机制在交易成功率和成功交易单元数分别提升了25%和28%,平台收益方面,双向拍卖机制较传统共享模式增加198元。

