变运营环境下基于混合主成分分析的结构损伤识别方法

黄海宾，臧敬刚

(1. 河北工业大学 土木与交通学院，天津 300401； 2. 河北工业大学 河北省土木工程技术研究中心，天津 300401)

0 引 言

近年来，基于振动的损伤识别方法在结构健康监测领域得到了广泛研究[1-2]。该类方法的基本依据是：损伤会引起结构动力特性(如频率、振型等模态参数)的变化，故可将动力特性作为结构的损伤特征，并通过动力特性变化判断其损伤状态[3-5]。然而，服役期内的运营环境(如温度、湿度、风速等因素)变化同样会引起结构动力特性的变化，这可能会掩盖损伤造成的动力特性变化，导致损伤识别效果不理想[6-11]。因此，在结构损伤识别中，剔除运营环境变化对损伤特征的影响至关重要。

从损伤特征中剔除运营环境变化的影响主要有两类方法[12]：①显式方法，建立环境变量与损伤特征之间的关系模型，进而量化运营环境变化的影响并予以剔除；②隐式方法，将环境变量视作隐藏变量嵌入到损伤特征中，进而估计运营环境变化的影响并予以剔除。隐式方法因无需测量环境变量却能考虑运营环境变化的影响，进而凸显出了实用价值，其中以主成分分析(principal-component analysis, PCA)应用最广。A. M. YAN等[6]将固有频率作为损伤特征，使用PCA成功剔除了环境效应对其损伤识别过程的影响；G. COMANDUCCI等[7]将PCA应用于某悬索桥，有效剔除了风速对固有频率的影响；F. UBERTINI等[8]提出将PCA与多元线性回归相结合，建立统计模型以剔除运营环境变化的影响，并采用某钟楼的固有频率数据进行了有效性验证；A. I. OZDAGLI等[9]使用振型和固有频率作为损伤特征，结合PCA剔除了温度变化的影响，提升了对某三层框架的损伤识别能力。

尽管基于PCA的损伤识别方法应用众多，但其适用范围仅局限于数据近似满足高斯分布且线性相关。目前，针对PCA在非线性问题中的局限性，学界已提出相关改进方法，A. M. YAN等[10]将PCA扩展为局部PCA，对非线性相关性进行分段线性化，剔除了运营环境变化对固有频率的非线性影响；E. REYNDERS等[11]针对变运营环境的非线性影响，提出了改进的核PCA方法，并采用某预应力混凝土桥的固有频率数据对其效果进行了验证。此外，非高斯分布在损伤特征数据中也普遍存在，赵人达等[13]和薛刚等[14]分别研究了不同太阳辐射强度下的混凝土箱梁温度场分布特性，结果表明箱梁底板、腹板和顶板的温度均呈非高斯分布，这会进一步造成损伤特征数据的非高斯分布。在结构损伤识别中，综合考虑数据的非高斯分布和非线性相关十分关键。

为有效处理运营环境变化下损伤特征数据的非高斯分布和非线性相关等问题，笔者提出一种基于混合PCA的结构损伤识别方法。利用高斯混合模型(gaussian mixture model, GMM)对存在非高斯分布和非线性相关的多维损伤特征数据进行建模，将其联合概率密度函数表示为多个局部高斯分量的线性组合，使得每个局部高斯分量内的数据之间满足线性相关性；然后，对所有局部高斯分量分别建立相应的PCA模型；再计算所有PCA模型残差部分的马氏平方距离和欧氏平方距离，将样本属于各高斯分量的后验概率作为权系数，对两类距离分别进行加权标准化以求得结构的综合损伤指标。最终，通过质量弹簧系统仿真和木桁架桥试验对其有效性进行验证。

1 传统PCA损伤识别

作为一种常用的多维数据分析方法，PCA可对由多个互相关特征变量构成的原始数据集进行线性变换以提取主成分，在保留绝大部分原始信息的前提下，降低变换后数据集的特征维度。原始数据集中各特征变量间的相关性越强，PCA的降维效果越显著。

令X=[x1,x2,…,xN]表示损伤特征矩阵，任意样本向量x均包含m个特征变量，共有N个样本。采用结构的多阶频率作为损伤特征，且各阶频率间存在相关性，故可通过PCA对特征数据集进行建模。PCA建模是利用如下特征值分解实现[15-16]：

∑=E[(x-μ)(x-μ)T]=QΛQT

(1)

式中：μ为数据集的均值向量；∑为数据集的协方差矩阵；Λ=diag(λ1,λ2,…,λm)为所有降序排列特征值构成的对角矩阵；Q=[q1,q2,…,qm]为与特征值对应的特征向量构成的标准正交矩阵；E(·)为期望算子。

PCA模型中特征值λi越大，则表明第i个主成分所包含的原始数据信息越多。当特征变量间存在强相关性时，仅需前面少数几个主成分即可近似重构原始数据。通常情况下，主成分个数d的选取原则如下：

(2)

式中：r为百分率，一般取95%，即主成分贡献率宜至少达到95%。当已知影响损伤特征的主导环境因素的个数时，可将d取为主导环境因素的个数。

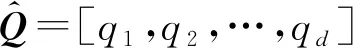
(3)

(4)

(5)

(6)

当数据服从或近似服从高斯分布时，令α表示显著性水平，指标DMah的阈值TMah由下式确定[17]：

(7)

(8)

2 混合PCA损伤识别

2.1 损伤特征的联合概率密度拟合

GMM利用多个高斯分量的线性组合对多维数据的概率密度函数进行拟合[18]。理论上讲，如果高斯分量的数目足够多，GMM能够准确拟合任意分布数据的概率密度函数。

经GMM拟合，多维损伤特征数据的概率密度函数具有如下形式：

(9)

(10)

(11)

进一步，可将GMM的最优参数估计问题转化为如下优化问题：

(12)

采用期望最大(expectation-maximization, EM)算法[19]求解该问题，首先设定GMM的初始参数为Θ(0)，然后分E步骤和M步骤进行迭代计算。E步骤依据当前参数Θ(i)，计算第j个样本向量xj属于第k个高斯分量的后验概率：

(13)

M步骤迭代更新参数Θ(i+1)：

(14)

(15)

(16)

重复E步骤和M步骤，直至收敛，即可得到GMM的最优参数。

在GMM拟合中，确定最佳的高斯分量数目是关键所在，采用可综合权衡模型拟合度与复杂度的贝叶斯信息准则对高斯分量的数目进行选择。

2.2 混合PCA建模与损伤指标计算

多维损伤特征数据经GMM拟合后，可获得所有高斯分量的均值向量和协方差矩阵，且任一高斯分量中的损伤特征之间存在线性相关性。由式(1)可知：PCA建模的实质是对协方差矩阵的特征值分解，故可依次对第k个高斯分量的协方差矩阵∑k分别进行特征值分解，从而得到K个PCA模型及其对应的用于计算损伤指标的残差子空间。

由于每个高斯分量对应的残差子空间不同，以其计算而得的损伤指标及阈值也会存在差异，故分别对马氏平方距离和欧氏平方距离进行加权标准化，作为混合PCA框架下的损伤指标。对于任意样本向量x而言，首先计算第k个高斯分量对应的损伤指标，即马氏平方距离DMah,k和欧氏平方距离DEuc,k；其次，通过相应的阈值TMah,k和TEuc,k分别对损伤指标进行标准化处理，即将损伤指标除以其阈值；最后，对所有标准化后的损伤指标进行加权求和，其权系数为该样本来自GMM各高斯分量的后验概率p(k|x)。具体表达式为：

(17)

(18)

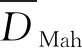
由于进行了加权标准化处理，两个综合损伤指标的阈值均为1。当损伤指标大于1时，判断结构处于损伤状态；反之，则判断结构处于无损状态。

2.3 损伤识别步骤

基于混合PCA的损伤识别方法，其实施过程分为离线建模和在线监测两个阶段。

2.3.1 离线建模

离线建模阶段，利用无损结构的损伤特征数据集进行混合PCA建模，步骤如下：

1)采用贝叶斯信息准则确定GMM的最佳高斯分量数目；

2)通过GMM对损伤特征数据的概率密度函数进行拟合；

3)分别对GMM中各高斯分量建立PCA模型并获得其对应的残差子空间；

4)计算GMM中各高斯分量所对应的马氏平方距离和欧氏平方距离的阈值。

2.3.2 在线监测

在线监测阶段，计算混合PCA框架下当前样本的损伤指标以判断结构损伤状态，步骤如下：

1)计算当前样本对应于GMM中各高斯分量的马氏平方距离和欧氏平方距离；

2)计算当前样本来自于GMM中各高斯分量的后验概率；

3)计算当前样本的加权标准马氏平方距离和加权标准欧氏平方距离作为损伤指标；

4)判断损伤状态，当损伤指标大于1时，判断结构处于损伤状态，反之则判断结构处于无损状态。

3 数值仿真

利用四自由度质量弹簧系统生成仿真数据，用以验证所提方法在变运营环境下的损伤识别能力。

质量弹簧系统共由4个质量块和5根弹簧组成，如图1。质量块的质量为：m1=m2=m3=m4=2 kg；弹簧的刚度与温度呈分段线性关系：

图1 质量弹簧系统

(19)

(20)

式中：ki,i=1,2,…,5为弹簧刚度；T为温度。

在0 ℃两侧，所有弹簧的刚度随温度的线性变化规律不同；第3根弹簧的刚度随温度的线性变化规律与其它弹簧的变化规律均不一致，这可用于模拟非线性效应。

以某桥梁监测系统采集的为期1年的空气温度数据(采样频率1 Hz，1 h内会得到多个样本，对这些样本取平均值，得到8 760个平均样本)为基准，等比例伸缩至[-20 ℃, 40 ℃]区间，作为数值仿真的温度输入值。通过无放回随机取样，首先取出5 400个温度样本输入质量弹簧系统，计算全部4阶固有频率即fn1、fn2、fn3和fn4，叠加一定程度的高斯噪声后，作为训练数据集；然后，分7次依次各取出480个温度样本输入质量弹簧系统，且每次均对第2根弹簧的刚度进行一定程度折减，在模拟运营环境变化和损伤同时存在情况下，计算全部4阶固有频率并叠加与训练数据集程度相同的高斯噪声后，作为测试数据集(共计7种工况)，如表1。

表1 测试数据集工况

该系统损伤前后的固有频率变化如图2。经对比分析可知：运营环境变化引起的固有频率变化会大部分甚至完全掩盖损伤引起的固有频率变化，故仅通过频率变化难以识别运营环境变化下的结构损伤。

图2 质量弹簧系统的固有频率变化

由贝叶斯信息准则确定最佳高斯分量数目为4，利用GMM对训练数据集的概率密度函数进行拟合(以fn1和fn2为例)。由图2可知：无损状态下fn1和fn2的变化幅度较大。图3(a)和图3(b)分别为fn1和fn2的频率直方图与GMM拟合概率密度函数间的对比，可知GMM能有效拟合非高斯分布数据的概率密度函数；图3(c)为fn1和fn2间的散点图，其表现出非线性相关性；图3(d)为GMM拟合的二维概率密度函数等高线图，可知GMM亦能有效处理数据中的非线性问题。

图3 频率fn1、fn2及 fn1与fn2间的GMM拟合效果

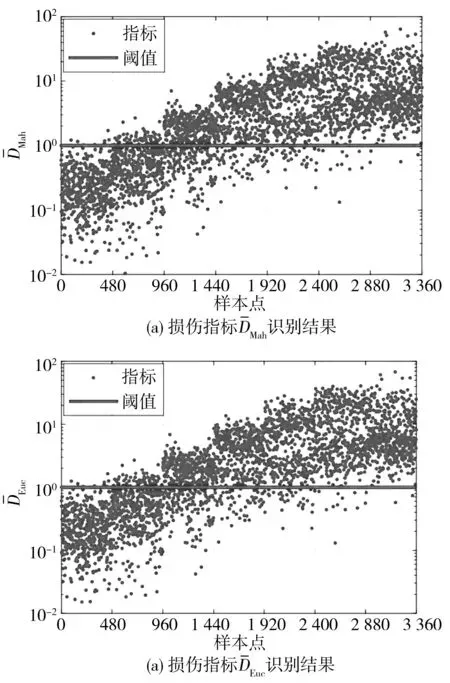
图4 混合PCA的损伤识别结果

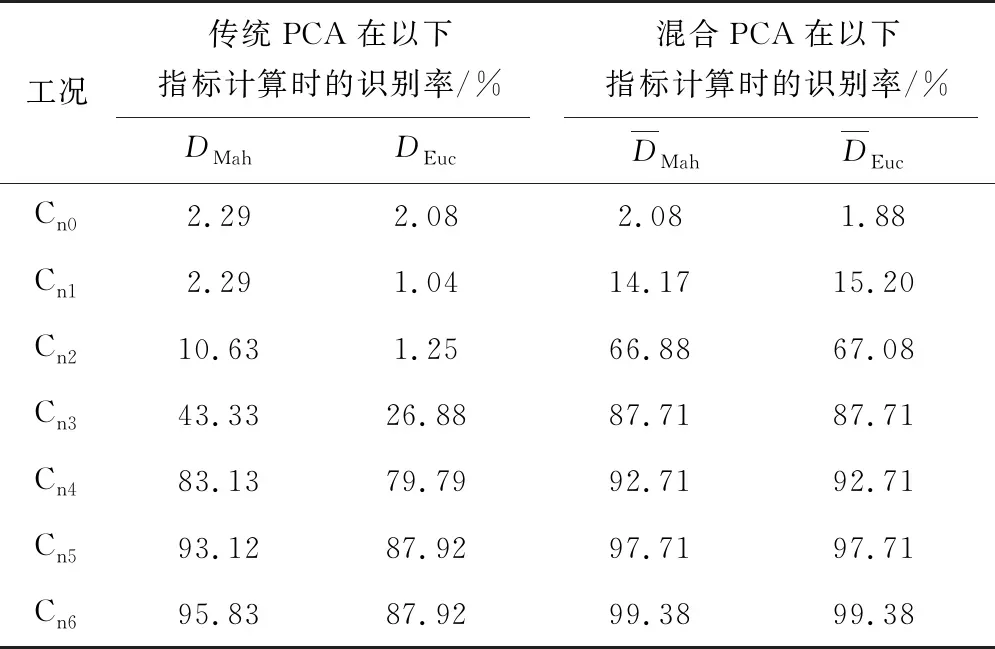
表2 PCA与混合PCA的损伤识别率

由表2可知：对工况Cn0，混合PCA的两种损伤指标对应的虚警率(对正常结构识别出损伤)较传统PCA均略低；对工况Cn1，混合PCA的识别效果优于传统PCA，但此时的微小损伤引起的固有频率变化不明显，漏警率(对损伤结构未识别出损伤)较高；对工况Cn2，混合PCA的损伤识别能力较传统PCA有了显著提升；对工况Cn3～Cn6，混合PCA的损伤识别率均接近或超过90%，且均大于传统PCA的损伤识别率，足见笔者方法的优越性。

4 试验验证

采用由芬兰的Kullaa课题组所完成的木桁架桥试验[20]进一步验证混合PCA的损伤识别效果。

桥总质量为36 kg，采用橡胶支座支撑，如图5。对结构施加随机白噪声激励，并在不同位置安装15个加速度计，以测量结构的加速度响应，采样频率为256 Hz，每次测量时长为32 s。测量期间，实验室内的温度和湿度不断发生变化。

图5 木桁架桥的试验布置

利用随机子空间方法对每次测量的振动数据进行模态参数识别，并采用较为可靠的第6、7、8、10、12和13阶固有频率(为后续方便，将它们依次记为ft1、ft2、ft3、ft4、ft5和ft6)作为损伤特征。在无损状态下，共获得1 871个有效的固有频率样本，通过无放回随机取样，选取1 671个样本作为训练数据集，剩余200个样本作为测试数据集的一部分；在距中跨左侧600 mm处的结构顶部附加不同质量，以模拟不同的损伤程度，共获得105个有效的固有频率样本，作为测试数据集的另一部分。因此，测试数据集中共包含6种工况，如表3。

表3 测试数据集工况

木桁架桥在环境影响下的固有频率变化如图6，图中虚线前为无损状态，虚线后为损伤状态。经对比计算可知：由环境变化引起的固有频率变化完全掩盖了损伤引起的固有频率变化，故仅通过频率变化无法识别运营环境变化下的结构损伤。

由贝叶斯信息准则确定最佳高斯分量数目为8，利用GMM对训练数据集的概率密度函数进行拟合。以ft2和ft6为例，由图6可知两频率在无损状态下的变化幅度较大；图7(a)和图7(b)分别为ft2和ft6的频率直方图与GMM拟合概率密度函数间的对比，可知GMM能有效拟合非高斯分布数据的概率密度函数；图7(c)为ft2和ft6间的散点图，其表现出非线性相关性；图7(d)为GMM拟合的二维概率密度函数等高线图，可知GMM能有效处理数据中的非线性问题。

图6 木桁架桥的固有频率变化

图7 频率ft2、ft6及ft2与ft6间的GMM拟合效果

图8 混合PCA的损伤识别结果

表4 PCA与混合PCA的损伤识别率

由表4可知：传统PCA中的欧氏平方距离并没有识别出结构损伤；传统PCA中的马氏平方距离虽有一定的识别效果，但并没有识别出工况Ct3的损伤；混合PCA中的加权标准欧氏平方距离的识别效果较传统PCA有了一定改善，但其对工况Ct3的识别效果仍不理想；混合PCA中的加权标准马氏平方距离对工况Ct2识别率达到了60.87%，对工况Ct3～Ct5识别率则均达到了100%，识别结果最好。综上，由于可有效处理非高斯分布和非线性相关等问题，混合PCA在损伤识别能力方面较传统PCA有显著提升。

7 结 论

笔者提出了变运营环境下基于混合PCA的结构损伤识别方法，并通过质量弹簧系统仿真和木桁架桥试验进行了有效性验证。得出如下结论：

1) 运营环境变化会引起结构损伤特征的非高斯分布和非线性相关等问题，致使传统PCA的损伤识别效果较差。

2) 在合理的高斯分量数目下，GMM能准确拟合多维损伤特征数据的联合概率密度函数，解决非高斯分布和非线性相关等问题。

3) 混合PCA的损伤识别能力较传统PCA而言有显著提升，其中以加权标准马氏平方距离的损伤识别能力最为优异。