锈蚀钢绞线混凝土黏结滑移本构模型研究
谢发祥,张川龙,李文祥
(河海大学 土木与交通学院,江苏 南京 210098)
0 引 言
先张法预应力空心板梁桥通常采用钢绞线施加预应力,是一种很常见的桥型[1]。服役一定年限后,受到复杂的环境及持续增加的车流量影响[2],该桥型在底板位置沿着桥梁纵向会出现大量的裂缝。钢筋锈蚀导致的黏结滑移性能退化是底板出现纵向裂缝的重要原因[3]。目前,对于锈蚀后钢筋混凝土黏结滑移关系如何退化问题,相关学者开展了研究。
试验研究方面主要通过拉拔来研究不同因素对于锈蚀后钢筋混凝土黏结的影响。罗文森等[4]制作了42个腐蚀拉拔试件,研究了变量为钢筋类别及锈蚀率;马亚飞等[5]基于快速腐蚀钢筋拉拔试验,研究了锈蚀率对抗弯强度的影响;李福海等[6]在电化学腐蚀的基础上,研究了锈蚀率对黏结强度的影响。董玉文等[7]通过室内试验,研究了冻融循环与锈蚀作用对钢筋混凝土试件界面黏结性能的影响。
理论研究方面主要集中在利用弹塑性力学的原理进行拉拔受力分析,建立考虑不同影响因素的黏结滑移关系计算模型。王潇舷等[8]采用数字图像相关(DIC)技术,基于弹性力学推导了钢筋锈胀应力模型;滕海文等[9]采用厚壁筒理论,对拉拔试件进行受力分析,得出了与试验结果吻合良好的黏结强度计算模型;王磊等[10]基于微小单元法的思想,根据加载端的荷载-位移关系建立了与锚固点位置有关的黏结滑移计算模型。
在有限元仿真模拟方面,方自虎等[11]利用ABAQUS研发了一个可以计算循环加载的单元,并通过试验得到了验证;李国一[12]等基于ABAQUS有限元软件,研究了钢筋混凝土动态黏结性能。
试验与理论相结合方面,王雪华[13]通过动态加载,测试了钢纤维混凝土荷载-位移曲线,得出了锈蚀率、钢纤维体积含量对黏结性能的影响;胡志坚等[14]在考虑混凝土材料受拉软化和损伤效应的基础上,建立了最大锈胀力公式计算公式;范亮等[15]通过21个试件的抗剪试验,建立了埋入式钢板混凝土界面黏结滑移本构方程。
综上所述,现有研究主要集中在普通钢筋与混凝土的黏结滑移性能方面,对于钢绞线与混凝土的黏结性能少有涉及。笔者开展了锈蚀钢绞线混凝土试件的拉拔试验,提出了黏结滑移本构模型,可以为研究底板纵向裂缝对先张法预应力空心板梁桥结构性能的影响提供基础。
1 试验概况
1.1 试验参数设计
浇筑12组试件(每组2个),目标锈蚀率为0%、5%、10%、20%,混凝土保护层厚度c为30、50、75 mm,试件具体参数和数量见表1。试件尺寸均为150 mm×150 mm×450 mm,混凝土强度为C40,钢绞线采用φ15.2mm,锚固长度为300 mm。在试件两端设置直径为20 mm的硬质PVC套管,形成无黏结段消除局部挤压效应。在距离PVC管25 mm的钢绞线中间区段焊接导线,连接恒流稳压电源,用于加快钢绞线的腐蚀速率,设计标准试件如图1。

表1 试件参数及数量
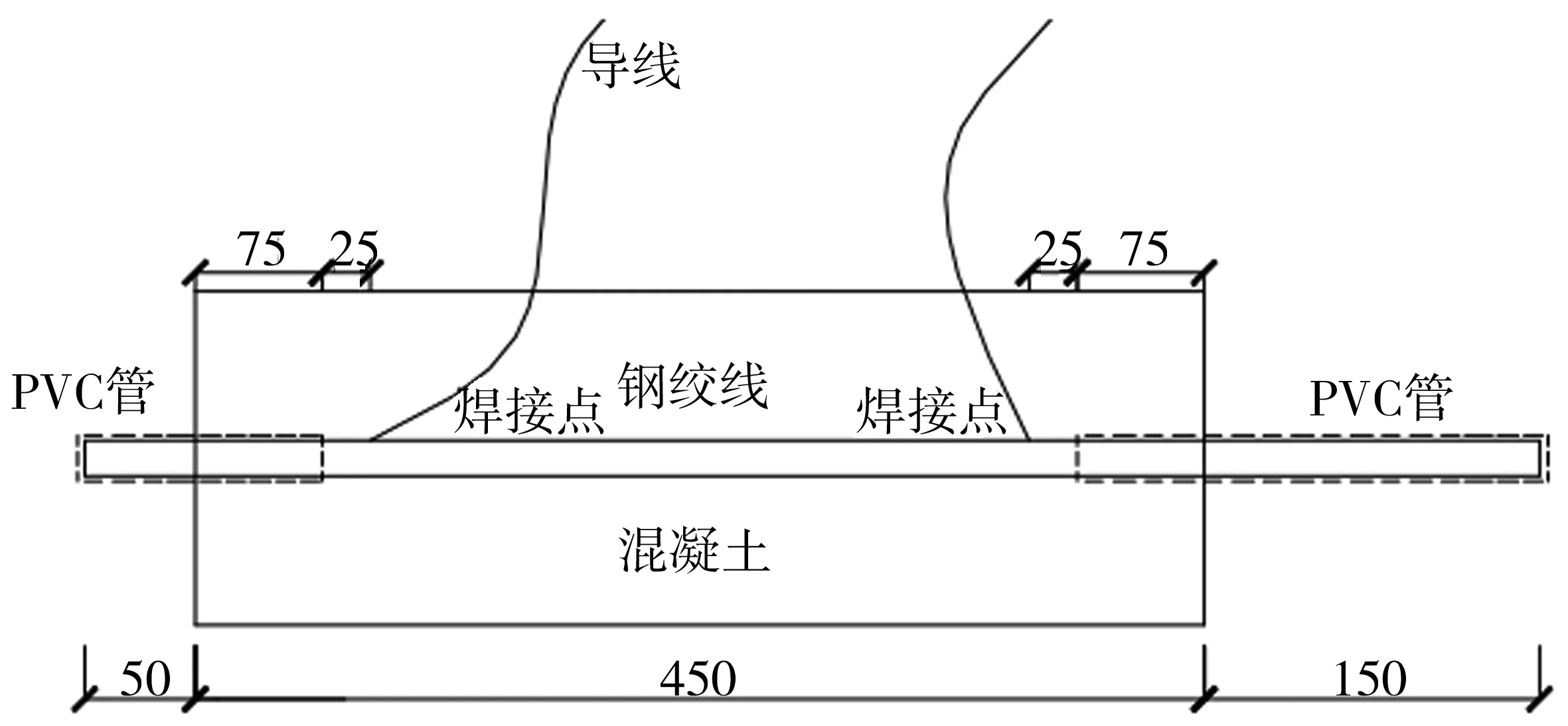
图1 设计标准试件(单位:mm)
1.2 试验原材料及试件制备
胶凝材料采用海螺牌P.O 42.5水泥。细骨料采用中砂,细度模数为2.3~3.0。粗骨料采用天然碎石,粒径为3.5~16 mm。采用城市自来水及萘系高效减水剂,减水率为12%~20%。混凝土质量配合比为水泥∶砂∶石∶水=1∶1.33∶2.42∶0.32。每立方米砼减水剂的用量为0.5 kg。浇筑完成后,将试件放入标准养护室(室温20 ℃±2 ℃,湿度≥95%)养护28 d后再放入5%的氯化钠溶液中浸泡1周,同时测得28 d混凝土标准立方体抗压试件的平均抗压强度为54.40 MPa。采用电化学加速腐蚀,通过控制电流强度和通电的时间来达到不同的锈蚀程度,恒流稳压锈蚀系统如图2。

图2 腐蚀系统
1.3 试验加载方案
不同锈蚀率及保护层厚度的试件拉拔试验由100 t液压伺服万能试验机MTS完成。加载过程采用位移控制,速度为0.04 mm/s。为得出钢绞线实际锈蚀率,劈裂后将取出的钢绞线两端做防锈部分切除,放入5%~8%的稀盐酸溶液中进行清洗,然后烘干称重,计算其实际锈蚀率ω平均值为0、3.5%、7.4%、15.2%。
2 试验结果
2.1 加载破坏形态
试验结果显示各试件破坏形式均为拔出-劈裂破坏,不同锈蚀率的试件破坏形态如图3。
锈蚀率较小时,混凝土试件出现沿着钢绞线的劈裂如图3(a)~图3(d);锈蚀率较大时,加载结束后,混凝土由于锈胀出现了剥落,如图3(e)~图3(f)。可以看到,当钢绞线不处于截面中心位置时,其裂缝主要集中在保护层厚度较薄的一面。对试件表面裂缝进行观测,并统计裂缝宽度信息见表2。

图3 试件破坏形态

表2 裂缝数量和宽度
由表2可以看出:在锈蚀率相同时,随着保护层厚度的增大,裂缝数量和宽度呈减小趋势;在保护层厚度相同时,裂缝数量随锈蚀率的增加基本保持不变,但裂缝宽度随锈蚀率的增加呈增大趋势。
2.2 荷载-位移曲线
将拉拔荷载-位移曲线如图4。由图4可知:当保护层厚度较厚(c=50、75 mm)时,荷载-位移曲线整体上由滑移段、劈裂段、下降段、残余段4部分组成;当保护层厚度较薄(c=30 mm)时,劈裂段几乎消失,荷载-位移曲线呈三角形分布。这说明随锈蚀率的增大,极限荷载及极限位移略有减小;随着保护层增大,极限荷载及极限位移均呈增大趋势。

图4 荷载-位移曲线
2.3 极限黏结强度及极限相对滑移量
对极限黏结强度τu进行计算,如式(1);对极限相对滑移量δu进行计算,如式(2)。
(1)
(2)
式中:Pu为极限拉拔力;d为钢绞线直径;l为钢绞线黏结区段长度;su为绝对位移量;Ep,Ec分别为钢绞线和混凝土的弹性模量;Ap,Ac分别为钢绞线和混凝土的截面面积。
对锈蚀率相同的试件极限黏结强度如图5(以ω=0、3.5%为例)。由图5可知:极限黏结强度与保护层厚度呈线性正相关。其原因是保护层越大,对钢绞线的约束越大,限制了裂缝的发展,因此极限黏结强度越大,采用式(3)进行线性拟合。

图5 极限黏结强度
(3)
式中:Kτ为曲线斜率;τ1为曲线截距。
取图5中的斜率和截距分析其随锈蚀率的变化规律,如图6。由图6可知:斜率和截距随锈蚀率增加呈线性减小趋势。

图6 斜率和截距随锈蚀率变化
对斜率、截距与锈蚀率对应点进行线性拟合并结合式(3),得到极限黏结强度的经验公式,如式(4):
(4)
同样可以得出极限相对滑移量的经验公式,如式(5):
(5)
将式(4)和(5)计算得出的极限黏结强度和极限相对滑移量与试验值进行比对,结果如图7。

图7 试验值和理论值对比
由图7可见,试件的极限黏结强度和极限相对滑移量理论值均匀地分布在45°线附近,说明式(4)、式(5)提出的极限黏结强度和极限相对滑移量的经验公式与实际情况吻合较好。
3 黏结滑移本构模型
3.1 考虑锈蚀率及保护层厚度的黏结滑移本构模型
参考规范《CEB-FIP model code 1990》提出的黏结滑移本构关系,在此基础上引入保护层厚度c、锈蚀率ω两个变量,提出改进的锈蚀钢绞线混凝土黏结滑移本构模型,该模型由4段折线组成,如图8。极限黏结强度τu和极限相对滑移δu可由式(4)、式(5)计算,为得出锈蚀钢绞线混凝土黏结滑移本构模型的具体数学表达式,还需对开裂黏结强度τ1、开裂相对滑移δ1、残余黏结强度τ2、残余相对滑移δ2共4个参数进行确定。为此,作以下定义:τ1=k1τu;δ1=k2δu;τ2=k3τu;δ2=k4δu。其中:k1,k2,k3,k4为比例系数。

图8 改进黏结滑移本构模型
选用显著性水平α=0.05,对试件试验得出的k1,k2,k3,k4进行正态分布假设检验。在检验前假设k1~k4均服从正态分布,根据检验结果来判断假设是否成立。假设检验结果如图9(以k1为例)。

图9 假设检验结果
图9检验结果显示参数k1服从正态分布。同理可得参数k2~k4均服从正态分布。统计参数的均值见表3。
通过对开裂黏结强度、残余黏结强度、开裂相对滑移、残余相对滑移4个参数的分析,将这4个参数与极限黏结强度和极限相对滑移建立关系,得出锈蚀钢绞线混凝土黏结滑移本构模型如式(6):
(6)
3.2 拉拔试验有限元模拟
为验证式(6)的准确性,将其应用于拉拔试验ABAQUS有限元模型中。模型尺寸与拉拔试件一致,根据保护层厚度不同,设置3种工况(c=30,50,75 mm);设置4种子工况(w=0、3.5%、7.4%、15.2%),子工况编号为1~4。混凝土采用C50,预应力钢绞线为ASTMA 416-92a标准270级钢绞线,屈服强度1 860 MPa,不同锈蚀率下的材料特性如表4。

表4 钢绞线材料特性表
混凝土采用8节点的三维减缩积分实体单元C3D8R模拟,钢绞线采用2节点三维线性梁单元B31模拟,混凝土采用弹性模型,钢绞线采用双线性模型。钢绞线与混凝土之间的黏结采用Spring2非线性弹簧单元模拟。
试验过程通过固定钢绞线混凝土试件,并对张拉端进行位移控制加载。在模型中对加载端混凝土面进行3个方向(x、y、z)的约束,采用位移加载方式对钢绞线拉拔端沿纵筋方向(即z方向)施加拉力,控制位移设为50 mm,试件模型如图10。

图10 拉拔试验有限元模型
混凝土和钢绞线间的黏结强度是非线性变化,并非简单的摩擦接触。为使有限元模拟准确可靠,将非线性弹簧单元Spring2作为混凝土与钢绞线间的连接接触。在ABAQUS中,只能输入线性弹簧单元,通过修改inp文件对混凝土和钢绞线间的接触进行修改,把混凝土和钢绞线共用节点一一对应,连接起来形成非线性弹簧单元,实现钢绞线与混凝土之间的黏结接触。
由于黏结滑移发生在切向方向(z方向),因此在法向(x、y方向)设置线性弹簧,弹簧刚度取x、y方向的较大值(105N/mm),以更好反应实际情况。切向方向弹簧单元刚度依据力-相对位移(F-δ)来确定,理论计算模型如图11,F计算如式(7)。

图11 黏结滑移理论计算模型(单位:mm)
F=π·D·dx·τ
(7)
式中:F为某节点处的拉力;D为钢绞线直径;dx为某节点处的单元尺寸;τ为某节点处的黏结应力,其黏结滑移本构关系如式(6)。
提取有限元仿真拉拔端荷载-位移曲线与试验值进行对比(以ω=3.5%为例),结果如图12。图中C30-3.5-1与C30-3.5-2分别为C30-3.5实验组两根试件。

图12 荷载-位移曲线对比
极限荷载与极限位移仿真值与试验值对比结果如图13。

图13 极限荷载及极限位移对比
由图12、图13可知:仿真计算得出的加载端荷载-位移曲线与试验值匹配度较高,其极限荷载及极限位移均匀地分布在45°线附近,说明式(6)能够较好描述锈蚀钢绞线混凝土试件黏结滑移退化过程。
4 结 论
通过对锈蚀钢绞线混凝土试件进行拉拔试验,针对不同保护层厚度、锈蚀率下试件黏结滑移性能进行研究,可以得到以下结论:
1)锈蚀相同时,随着保护层厚度增大,裂缝数量和宽度呈减小趋势,且当钢绞线不处于截面中心位置时,裂缝主要集中在保护层厚度较薄的一面;对于同等保护层厚度下,裂缝数量随锈蚀率的增加基本保持不变,但裂缝宽度随锈蚀率增加而增大。
2)保护层厚度相同时,极限黏结强度及极限相对滑移量随锈蚀率增大呈线性减小趋势。在锈蚀率相同时,极限黏结强度及极限相对滑移量与保护层厚度呈线性正相关。通过线性拟合,建立了包含保护层厚度、锈蚀率的极限黏结强度和极限相对滑移量的经验公式,并将理论值和试验值对比,结果显示两者误差较小,吻合度较高。
3)将开裂黏结强度、残余黏结强度与极限黏结强度建立线性关系,将开裂相对滑移、残余相对滑移与极限相对滑移建立线性关系,得到了保护层厚度和锈蚀率的表达式。参考《CEB-FIP model code 1990》提出的黏结滑移本构关系,引入保护层、锈蚀率2个变量,提出改进后的锈蚀钢绞线混凝土黏结滑移本构模型。仿真模型计算结果显示:笔者提出的锈蚀钢绞线混凝土黏结滑移本构模型可以较好地描述锈蚀钢绞线混凝土试件黏结滑移退化行为。

